中学受験直前ピックアップ！あなたは解けるかな？小学4年生を悩ませた算数チャレンジ問題！ #shorts #算数 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 中学受験直前ピックアップ！あなたは解けるかな？小学4年生を悩ませた算数チャレンジ問題！ #shorts #算数

中学受験直前ピックアップ！あなたは解けるかな？小学4年生を悩ませた算数チャレンジ問題！ #shorts #算数

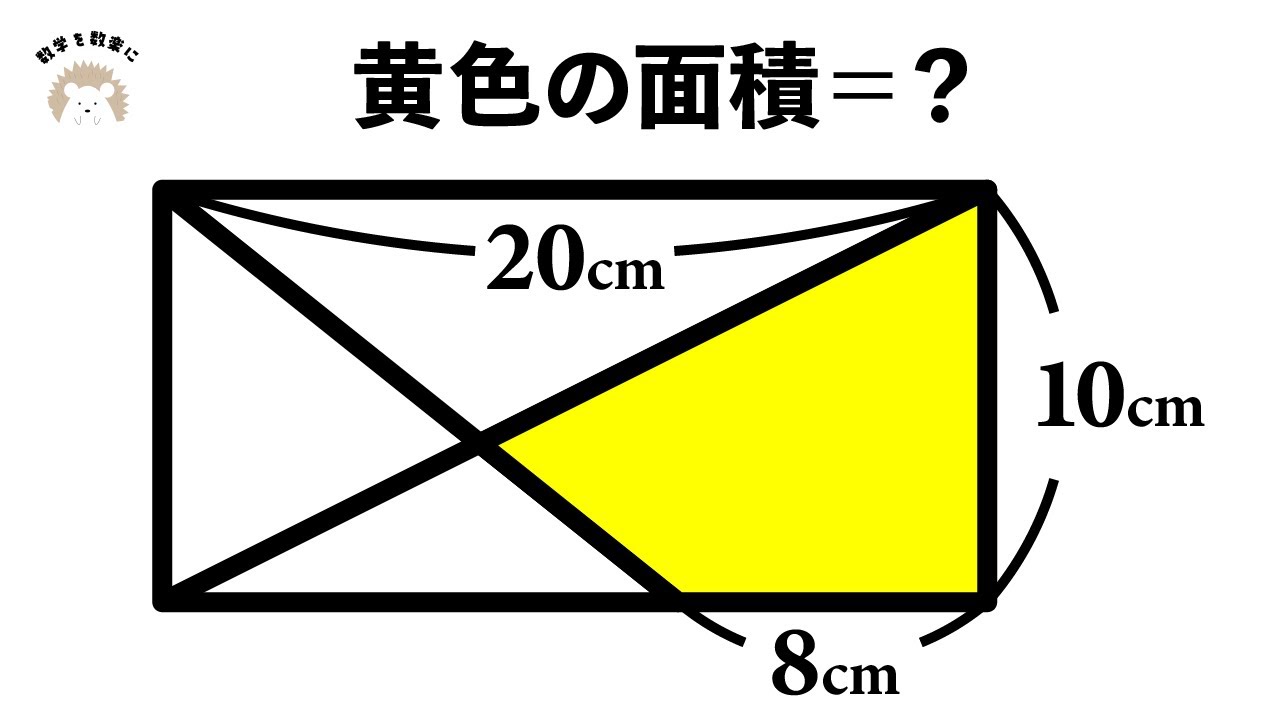
問題文全文(内容文)：
小学4年生を悩ませた算数チャレンジ問題に関して解説していきます.
単元： #算数(中学受験)
指導講師： 理数個別チャンネル
問題文全文(内容文)：
小学4年生を悩ませた算数チャレンジ問題に関して解説していきます.
投稿日：2024.01.24

＜関連動画＞

大谷翔平の時給は？

アイキャッチ画像
単元： #単位・比と割合・比例・反比例#売買損益と食塩水
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
大谷翔平の時給に関して解説していきます。
この動画を見る　

【受験算数】つるかめ算：つるかめ算をマスターしよう！その2　表を利用②

アイキャッチ画像
単元： #算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師： 理数個別チャンネル
問題文全文(内容文)：
つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。
この動画を見る　

【受験算数】つるかめ算：つるかめ算をマスターしよう！その3　計算を利用

アイキャッチ画像
単元： #算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師： 理数個別チャンネル
問題文全文(内容文)：
つるとかめが合計8匹います。足の合計が26本です。それぞれ何匹いるでしょう。
この動画を見る　

【受験算数】平面図形と比：（基本❹）2辺比の積から面積比【予習シリーズ演習問題集・小5下】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#相似と相似を利用した問題
教材： #予習シ#予習シ演問・小5下#中学受験教材#平面図形と比(1)
指導講師： 理数個別チャンネル
問題文全文(内容文)：
右図の三角形ABCで AD：DB＝1：1 BE：EC＝3：2 CF：FA＝3：1 です。次の問いに答えよ。
(1)三角形DBEの面積は、三角形ABCの面積の何分のいくつか。 (2)三角形DEFの面積は、三角形ABCの面積の何分のいくつか。
この動画を見る　

補助線の引き方　3通りで解説

アイキャッチ画像
単元： #数学(中学生)#中２数学#平面図形#角度と面積#三角形と四角形
指導講師： 数学を数楽に
問題文全文(内容文)：
CD=?
＊図は動画内参照
この動画を見る　
PAGE TOP