 とある男が授業をしてみた
とある男が授業をしてみた
 とある男が授業をしてみた
とある男が授業をしてみた
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【割合難問】中3冬特訓(特別編)

単元:
#数学(中学生)#中3数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①
ある商品をいくつか仕入れた。
この商品を定価の25%引きで売ったとき、仕入れた個数の 5%が売れ残っても、仕入れ総額の14%以上の利益が出るようにしたい。定価を仕入れ値の何%増し以上にすればよいか答えなさい。
この動画を見る
①
ある商品をいくつか仕入れた。
この商品を定価の25%引きで売ったとき、仕入れた個数の 5%が売れ残っても、仕入れ総額の14%以上の利益が出るようにしたい。定価を仕入れ値の何%増し以上にすればよいか答えなさい。
【12/30】中3冬特訓6日目
単元:
#中3数学
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①
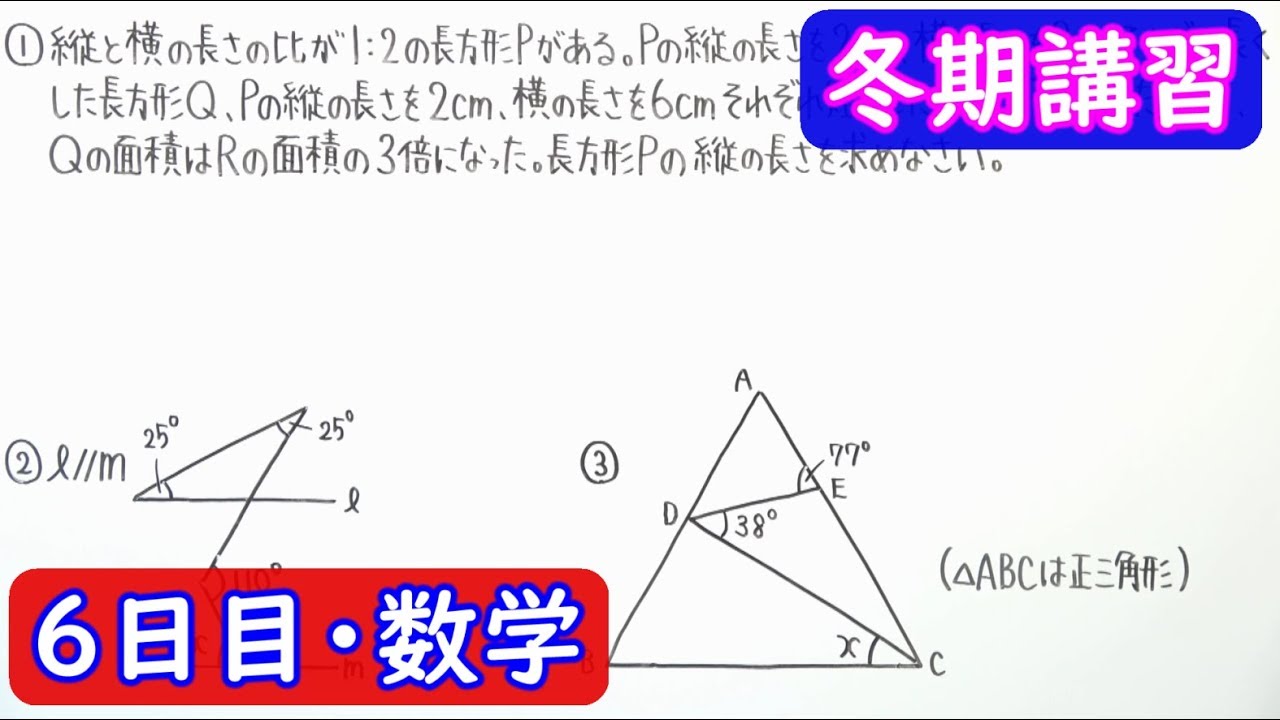
縦と横の長さの比が1:2の長方形Pがある。
Pの縦の長さを2cm、横の長さを2cmそれぞれ長くした長方形Q、Pの縦の長さを2cm、横の長さを6cmそれぞれ短くした長方形Rをつくったところ、Qの面積はRの面積の3倍になった。長方形Pの縦の長さを求めなさい。
この動画を見る
①
縦と横の長さの比が1:2の長方形Pがある。
Pの縦の長さを2cm、横の長さを2cmそれぞれ長くした長方形Q、Pの縦の長さを2cm、横の長さを6cmそれぞれ短くした長方形Rをつくったところ、Qの面積はRの面積の3倍になった。長方形Pの縦の長さを求めなさい。
【12/29】中3冬特訓5日目

単元:
#英語(中学生)#中3英語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①My father took these pictures. → These pictures ( ) ( ) my father.
➁Who broke that window? → Who ( ) that window ( ) ( )?
③Watching birds is intersting to her. → She is ( ) ( ) watching birds.
④Our school ( ) built fifty years ago.
⑤Risa was surprised ( ) her father's letter.
⑥Mt.Fuji was covered ( ) ( ) snow.
⑦These animals are made ( ) ( ) paper.
⑧The zoo is crowded ( ) children.
この動画を見る
①My father took these pictures. → These pictures ( ) ( ) my father.
➁Who broke that window? → Who ( ) that window ( ) ( )?
③Watching birds is intersting to her. → She is ( ) ( ) watching birds.
④Our school ( ) built fifty years ago.
⑤Risa was surprised ( ) her father's letter.
⑥Mt.Fuji was covered ( ) ( ) snow.
⑦These animals are made ( ) ( ) paper.
⑧The zoo is crowded ( ) children.
【トンネル】中3冬特訓(特別編)

単元:
#数学(中学生)#中3数学
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①
あるトンネルに、A列車が秒速30mで入り始めた。この10秒後に反対側からB列車が秒速40mで入り始めた。その後、2つの列車はトンネルの中央で出会ったという。
このトンネルの長さを求めなさい。
この動画を見る
①
あるトンネルに、A列車が秒速30mで入り始めた。この10秒後に反対側からB列車が秒速40mで入り始めた。その後、2つの列車はトンネルの中央で出会ったという。
このトンネルの長さを求めなさい。
【12/28】中3冬特訓4日目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#2次方程式#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$x^3+x^2-x-1$を因数分解しなさい。
➁関数$y=ax^2$は$x$の変域が$-4 \leqq x \leqq3$のとき、$y$の変域が$0 \leqq y \leqq8$である。
$x$の値が1から5まで増加するとき、この関数の変化の割合を求めよ。
③二次方程式$x^2-ax-5=0$の解の1つが$x=5$のとき、$a$の値ともう一つの解を求めよ。
④$\sqrt{6a}$を小数第一位で四捨五入すると2になるような整数$a$を求めよ。
この動画を見る
①$x^3+x^2-x-1$を因数分解しなさい。
➁関数$y=ax^2$は$x$の変域が$-4 \leqq x \leqq3$のとき、$y$の変域が$0 \leqq y \leqq8$である。
$x$の値が1から5まで増加するとき、この関数の変化の割合を求めよ。
③二次方程式$x^2-ax-5=0$の解の1つが$x=5$のとき、$a$の値ともう一つの解を求めよ。
④$\sqrt{6a}$を小数第一位で四捨五入すると2になるような整数$a$を求めよ。
【12/27】中3冬特訓3日目

単元:
#英語(中学生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①
Season
teach
➁
already
taught
③
school
cheese
④
brought
caught
⑤
summer
last
⑥
March
warm
⑦
around
young
⑧
write
build
⑨
working
first
➉
summer
busy
⑪
lie
knife
⑫
many
said
この動画を見る
①
Season
teach
➁
already
taught
③
school
cheese
④
brought
caught
⑤
summer
last
⑥
March
warm
⑦
around
young
⑧
write
build
⑨
working
first
➉
summer
busy
⑪
lie
knife
⑫
many
said
【12/26】中3冬特訓2日目

単元:
#数学(中学生)#中3数学
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$\sqrt{32}-2\sqrt{3} \times \sqrt{6}$
➁$\sqrt{3}-\sqrt{27} + \sqrt{48}$
③$7\sqrt{2}-\sqrt{18} + \frac{8}{\sqrt{2}}$
④
列車が鉄橋を渡り始めてから渡り終わるまでにかかる時間は、長さ 200mの普通列車では30秒、長さ160mの特急列車では14秒であった。 また、特急列車の速さは普通列車の速さの2倍であった。
この鉄橋の長さは何mか求めなさい。
この動画を見る
①$\sqrt{32}-2\sqrt{3} \times \sqrt{6}$
➁$\sqrt{3}-\sqrt{27} + \sqrt{48}$
③$7\sqrt{2}-\sqrt{18} + \frac{8}{\sqrt{2}}$
④
列車が鉄橋を渡り始めてから渡り終わるまでにかかる時間は、長さ 200mの普通列車では30秒、長さ160mの特急列車では14秒であった。 また、特急列車の速さは普通列車の速さの2倍であった。
この鉄橋の長さは何mか求めなさい。
【12/25】中3冬特訓1日目

単元:
#英語(中学生)#中3英語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①You (at better, go. had once) to the hospital.
あなたはすぐに病院に行った方がいい。
➁He is (next. enjoy going fishing to) Sunday.
彼は次の日曜日につりを楽しむでしょう。
③They (see to movie ought that).
彼らはあの映画を見るべきです。
④They must practice soccer hard. → They ( ) ( ) practice soccer hard.
⑤She couldn't find her notebook. → She ( ) ( ) to find her notebook.
⑥( ) go shopping this afternoon. → Shall ( ) go shopping this afternoon.
この動画を見る
①You (at better, go. had once) to the hospital.
あなたはすぐに病院に行った方がいい。
➁He is (next. enjoy going fishing to) Sunday.
彼は次の日曜日につりを楽しむでしょう。
③They (see to movie ought that).
彼らはあの映画を見るべきです。
④They must practice soccer hard. → They ( ) ( ) practice soccer hard.
⑤She couldn't find her notebook. → She ( ) ( ) to find her notebook.
⑥( ) go shopping this afternoon. → Shall ( ) go shopping this afternoon.
【高校数学】数Ⅲ-124 変曲点とグラフの対称性

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(変曲点とグラフの対称性)
Q. 曲線$C:y=x^3+3ax+b$について次の問いに答えよ。
①Cの変曲点Pの座標を求めよ。
②Cは点Pに関して点対称であることを示せ。
この動画を見る
数Ⅲ(変曲点とグラフの対称性)
Q. 曲線$C:y=x^3+3ax+b$について次の問いに答えよ。
①Cの変曲点Pの座標を求めよ。
②Cは点Pに関して点対称であることを示せ。
【高校数学】数Ⅲ-123 第2次導関数とグラフ④

単元:
#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(第2次導関数とグラフ④)
①$x^2-xy-y+x+2=0$の漸近線を求めよ。
➁$y=(\log x)^2$の概形を書け。
この動画を見る
数Ⅲ(第2次導関数とグラフ④)
①$x^2-xy-y+x+2=0$の漸近線を求めよ。
➁$y=(\log x)^2$の概形を書け。
【高校数学】数Ⅲ-122 第2次導関数とグラフ③

単元:
#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(第2次導関数とグラフ③)
①曲線$\frac{x^2-3x+4}{2x-2}$の概形を書け。
この動画を見る
数Ⅲ(第2次導関数とグラフ③)
①曲線$\frac{x^2-3x+4}{2x-2}$の概形を書け。
【高校数学】数Ⅲ-121 第2次導関数とグラフ②

単元:
#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(第2次導関数とグラフ➁)
①曲線$y=x+\frac{1}{x}$の概形を書け。
この動画を見る
数Ⅲ(第2次導関数とグラフ➁)
①曲線$y=x+\frac{1}{x}$の概形を書け。
【何秒で終わる?】ルートの変形特訓

単元:
#数学(中学生)#中3数学#平方根
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1 $\sqrt{8}=$
2 $\sqrt{9}=$
3 $\sqrt{12}=$
4 $\sqrt{6}=$
5 $\sqrt{20}=$
6 $\sqrt{4}=$
7 $\sqrt{18}=$
8 $\sqrt{32}=$
9 $\sqrt{15}=$
10 $\sqrt{24}=$
11 $\sqrt{100}=$
12 $\sqrt{40}=$
13 $\sqrt{25}=$
14 $\sqrt{45}=$
15 $\sqrt{30}=$
16 $\sqrt{600}=$
17 $\sqrt{16}=$
18 $\sqrt{50}=$
19 $\sqrt{28}=$
20 $\sqrt{72}=$
21 $\sqrt{56}=$
22 $\sqrt{38}=$
23 $\sqrt{75}=$
24 $\sqrt{1000}=$
25 $\sqrt{80}=$
26 $\sqrt{98}=$
27 $\sqrt{33}=$
28 $\sqrt{20000}=$
29 $\sqrt{90000}=$
30 $\sqrt{1200000}=$
この動画を見る
1 $\sqrt{8}=$
2 $\sqrt{9}=$
3 $\sqrt{12}=$
4 $\sqrt{6}=$
5 $\sqrt{20}=$
6 $\sqrt{4}=$
7 $\sqrt{18}=$
8 $\sqrt{32}=$
9 $\sqrt{15}=$
10 $\sqrt{24}=$
11 $\sqrt{100}=$
12 $\sqrt{40}=$
13 $\sqrt{25}=$
14 $\sqrt{45}=$
15 $\sqrt{30}=$
16 $\sqrt{600}=$
17 $\sqrt{16}=$
18 $\sqrt{50}=$
19 $\sqrt{28}=$
20 $\sqrt{72}=$
21 $\sqrt{56}=$
22 $\sqrt{38}=$
23 $\sqrt{75}=$
24 $\sqrt{1000}=$
25 $\sqrt{80}=$
26 $\sqrt{98}=$
27 $\sqrt{33}=$
28 $\sqrt{20000}=$
29 $\sqrt{90000}=$
30 $\sqrt{1200000}=$
【時事問題】2018.11月②

単元:
#社会(中学生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
時事問題(2018年11月②)
・広い範囲で関税の撤廃やサービス・投資の自由化を進める(①)が12月30日に発効する。
・(➁)選手が大リーグ新人王に選ばれた。日本選手では(③)人目。
・2022年度をめどに、防衛省は自衛隊に(④)部隊をつくる!?
・マサチューセッツ工科大学の研究チームが(⑤)の開発に成功!?
この動画を見る
時事問題(2018年11月②)
・広い範囲で関税の撤廃やサービス・投資の自由化を進める(①)が12月30日に発効する。
・(➁)選手が大リーグ新人王に選ばれた。日本選手では(③)人目。
・2022年度をめどに、防衛省は自衛隊に(④)部隊をつくる!?
・マサチューセッツ工科大学の研究チームが(⑤)の開発に成功!?
【時事問題】2018.11月①

単元:
#社会(中学生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
時事問題(2018年11月①)
・フィギュアスケートのグランプリシリーズ(女子)の第4戦、第6戦で(①)選手が優勝し、ファイナル進出を決めた。
・NASAの新型探査機(➁)が火星に着陸した。
・2025年の万博が(③)市で開かれることが決まった。会場は湾岸部の人工島(④)。
・日産自動車の会長だった(⑤)が逮捕された。
・外国人労働者の受け入れ拡大に向けた(⑥)法の改正案が衆議院を通過した。
この動画を見る
時事問題(2018年11月①)
・フィギュアスケートのグランプリシリーズ(女子)の第4戦、第6戦で(①)選手が優勝し、ファイナル進出を決めた。
・NASAの新型探査機(➁)が火星に着陸した。
・2025年の万博が(③)市で開かれることが決まった。会場は湾岸部の人工島(④)。
・日産自動車の会長だった(⑤)が逮捕された。
・外国人労働者の受け入れ拡大に向けた(⑥)法の改正案が衆議院を通過した。
【高校受験対策】数学-死守35

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#1次関数#平行と合同#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守35
①$6a \div -(\frac{3}{2})$
➁$9-(-15)\div3$
③$\sqrt{54}+4\sqrt{6}$
④$4x^2 \times -\frac{5}{6}xy$
⑤$\sqrt{18}-\frac{4}{\sqrt{2}}$
⑥
$2x+5y=3$
$x-3y=7$
⑦$x=19$のとき、$x^2-10x+9$の値を求めなさい。
⑧2次方程式$x^2+3x-0$を解きなさい
⑨直線$y=-x+7$に平行で、点$(4,-1)$を通る直線の式を求めなさい。
⑩右の図のような五角柱ABCDEFGHIJにおいて、 辺AFとねじれの位置にある辺の数を求めなさい。
⑪半径が$6cm$、中心角が$40°$のおうぎ形の面積を求めなさい。 ただし円周率は$\pi$とする。
⑫$8\leqq \sqrt{n} \leqq9$にあてはまる自然数$n$は、全部で何個あるか求めなさい。
⑬
袋の中に赤玉が3個、白玉が2個入っています。
この袋の中から2個の玉を同時に取り出すとき、取り出した2個の玉が同じ色である確率を求めなさい。ただし、どの玉の取り出し方も同様に確からしいものとします。
⑭
底面の半径が$4cm$で、表面積が$84\pi cm^2$の円柱がある。
この円柱の体積を求めなさい。ただし円周率は$\pi$とする。
この動画を見る
高校受験対策・死守35
①$6a \div -(\frac{3}{2})$
➁$9-(-15)\div3$
③$\sqrt{54}+4\sqrt{6}$
④$4x^2 \times -\frac{5}{6}xy$
⑤$\sqrt{18}-\frac{4}{\sqrt{2}}$
⑥
$2x+5y=3$
$x-3y=7$
⑦$x=19$のとき、$x^2-10x+9$の値を求めなさい。
⑧2次方程式$x^2+3x-0$を解きなさい
⑨直線$y=-x+7$に平行で、点$(4,-1)$を通る直線の式を求めなさい。
⑩右の図のような五角柱ABCDEFGHIJにおいて、 辺AFとねじれの位置にある辺の数を求めなさい。
⑪半径が$6cm$、中心角が$40°$のおうぎ形の面積を求めなさい。 ただし円周率は$\pi$とする。
⑫$8\leqq \sqrt{n} \leqq9$にあてはまる自然数$n$は、全部で何個あるか求めなさい。
⑬
袋の中に赤玉が3個、白玉が2個入っています。
この袋の中から2個の玉を同時に取り出すとき、取り出した2個の玉が同じ色である確率を求めなさい。ただし、どの玉の取り出し方も同様に確からしいものとします。
⑭
底面の半径が$4cm$で、表面積が$84\pi cm^2$の円柱がある。
この円柱の体積を求めなさい。ただし円周率は$\pi$とする。
【高校受験対策】数学-関数38
単元:
#数学(中学生)#中2数学#1次関数#平行と合同
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数38
Q.
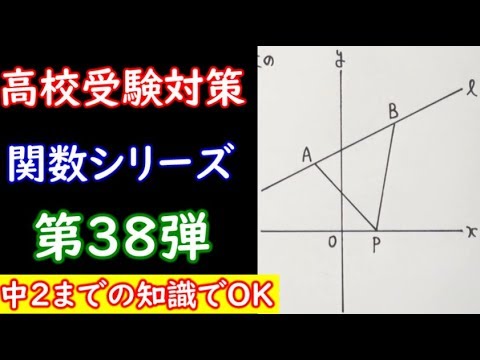
右の図で、直線$l$は関数$y=\frac{1}{2}x+6$のグラフです。点$A$・点$B$は直線$l$上の点で、点$A$の座標は$(-2,5)$、点$B$の座標は$(4,8)$です。 このとき次の各問に答えなさい。
①2点、$o,A$を通る直線の傾きを求めなさい。
点$P$は$x$軸上の$x>0$の部分にあり、$△APB$の面積は$26cm^2$です。
②点$P$の座標を求めなさい。
③点$P$を通り、$△APB$の面積を2等分する直線の式を求めなさい。
この動画を見る
高校受験対策・関数38
Q.
右の図で、直線$l$は関数$y=\frac{1}{2}x+6$のグラフです。点$A$・点$B$は直線$l$上の点で、点$A$の座標は$(-2,5)$、点$B$の座標は$(4,8)$です。 このとき次の各問に答えなさい。
①2点、$o,A$を通る直線の傾きを求めなさい。
点$P$は$x$軸上の$x>0$の部分にあり、$△APB$の面積は$26cm^2$です。
②点$P$の座標を求めなさい。
③点$P$を通り、$△APB$の面積を2等分する直線の式を求めなさい。
【高校数学】数Ⅲ-120 第2次導関数とグラフ①

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(第2次導関数とグラフ①)
ポイント
$f''(x) \gt 0$となる区間では①に凸、$f''(x) \lt 0$となる区間では➁に凸である。
$f''(a) =0$のとき、$x=a$の前後で$f''(x)$の符号が変わるなら、点$(a,f(a))$は③点。
④曲線$y=x^4-4x^2+1$の凹凸を調べよ
この動画を見る
数Ⅲ(第2次導関数とグラフ①)
ポイント
$f''(x) \gt 0$となる区間では①に凸、$f''(x) \lt 0$となる区間では➁に凸である。
$f''(a) =0$のとき、$x=a$の前後で$f''(x)$の符号が変わるなら、点$(a,f(a))$は③点。
④曲線$y=x^4-4x^2+1$の凹凸を調べよ
【高校数学】数Ⅲ-119 関数の極限④

単元:
#関数と極限#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(関数の極値④)
①関数$f(x)=x^2e^{ax}$が$x=1$で極値をとるような定数$a$の値とそのときの極値を求めよ。
➁関数$f(x)=\frac{ax+b}{x^2+1}$が$x=1$で極大値$2$を持つような定数$a,b$を求めよ。
この動画を見る
数Ⅲ(関数の極値④)
①関数$f(x)=x^2e^{ax}$が$x=1$で極値をとるような定数$a$の値とそのときの極値を求めよ。
➁関数$f(x)=\frac{ax+b}{x^2+1}$が$x=1$で極大値$2$を持つような定数$a,b$を求めよ。
【高校数学】数Ⅲ-118 関数の極値③

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(関数の極値③)
Q.次の極値を求めなさい。
①$f(x)=x+ 2\cos x(0\leqq x\leqq \pi)$
➁$f(x)=\sin x(1+ \cos x)(0\leqq x\leqq 2\pi)$
この動画を見る
数Ⅲ(関数の極値③)
Q.次の極値を求めなさい。
①$f(x)=x+ 2\cos x(0\leqq x\leqq \pi)$
➁$f(x)=\sin x(1+ \cos x)(0\leqq x\leqq 2\pi)$
【高校数学】数Ⅲ-117 関数の極値②

単元:
#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(関数の極値➁)
Q.次の関数の極値を求めなさい
①$f(x)=x\sqrt{1-x^2}$
➁$f(x)=|x|\sqrt{x+3}$
この動画を見る
数Ⅲ(関数の極値➁)
Q.次の関数の極値を求めなさい
①$f(x)=x\sqrt{1-x^2}$
➁$f(x)=|x|\sqrt{x+3}$
【時事問題】2018.10月後半

単元:
#社会(中学生)#歴史
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
時事問題(2018.10月後半)
・環境省は2030年までの目標として、使い捨てプラスチック排出量の(①%削減)を戦略に盛り込むことを発表。レジ袋は早ければ(➁年)に有料化となる。
・2019年から、英検のライティングとスピーキングの一部でに(③)よる採点が始まる。
・来年(④月)に消費税率が(⑤%)に引き上がる。
・アメリカのトランプ大統領は、旧ソ連と結んでいた(⑥条約)を破棄する方針を発表。
・琉球王国の陵墓(⑦)が国宝に指定された。
この動画を見る
時事問題(2018.10月後半)
・環境省は2030年までの目標として、使い捨てプラスチック排出量の(①%削減)を戦略に盛り込むことを発表。レジ袋は早ければ(➁年)に有料化となる。
・2019年から、英検のライティングとスピーキングの一部でに(③)よる採点が始まる。
・来年(④月)に消費税率が(⑤%)に引き上がる。
・アメリカのトランプ大統領は、旧ソ連と結んでいた(⑥条約)を破棄する方針を発表。
・琉球王国の陵墓(⑦)が国宝に指定された。
【高校受験対策】数学-死守34

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守34
①$(-8)+(-4)$
②$-\frac{5}{7}+\frac{2}{3}$
③$65a^2b \div5a$
④$\frac{18}{\sqrt{2}}-\sqrt{98}$
⑤$(x+9)^2-(x-3)(x-7)$
⑥$(x+4)^2-2(x+4)-24$を因数分解しなさい。
⑦2次方程式$6x^2-2x-1=0$を解きなさい。
⑧関数$y=ax^2$について、$x$の値が$2$から$5$まで増加するときの変化の割合が$ー4$であった。このときの$a$の値を求めなさい。
④1本$a$円のえんぴつを9本と1個100円の消しゴムを1個買って1000円を支払い、おつりを受け取った。
このときの数量の関係を不等式で表しなさい。ただし、右辺は1000だけとする。
⑩$\sqrt{53-2n}$が整数となるような正の整数$n$をすべて書きなさい。
⑪
Aさんの家からバス停までの道のりは$a$km、バス停から駅までの道のりは$b$kmである。Aさんが、Aさんの家からバス停までは時速4kmで歩き、バス停から駅までは時速30kmで走るバスに乗ったところ、 Aさんの家から駅まで$t$時間かかった。
このとき、$t$を$a$と$b$を使った式で表しなさい。 ただし、バス停でバスを待つ時間は考えないものとする。
⑫
右の度数分布表は、あるクラスの生徒20人のハンドボール投げの記録をまとめたものである。この度数分布表から求められる記録の平均値を求めなさい。
この動画を見る
高校受験対策・死守34
①$(-8)+(-4)$
②$-\frac{5}{7}+\frac{2}{3}$
③$65a^2b \div5a$
④$\frac{18}{\sqrt{2}}-\sqrt{98}$
⑤$(x+9)^2-(x-3)(x-7)$
⑥$(x+4)^2-2(x+4)-24$を因数分解しなさい。
⑦2次方程式$6x^2-2x-1=0$を解きなさい。
⑧関数$y=ax^2$について、$x$の値が$2$から$5$まで増加するときの変化の割合が$ー4$であった。このときの$a$の値を求めなさい。
④1本$a$円のえんぴつを9本と1個100円の消しゴムを1個買って1000円を支払い、おつりを受け取った。
このときの数量の関係を不等式で表しなさい。ただし、右辺は1000だけとする。
⑩$\sqrt{53-2n}$が整数となるような正の整数$n$をすべて書きなさい。
⑪
Aさんの家からバス停までの道のりは$a$km、バス停から駅までの道のりは$b$kmである。Aさんが、Aさんの家からバス停までは時速4kmで歩き、バス停から駅までは時速30kmで走るバスに乗ったところ、 Aさんの家から駅まで$t$時間かかった。
このとき、$t$を$a$と$b$を使った式で表しなさい。 ただし、バス停でバスを待つ時間は考えないものとする。
⑫
右の度数分布表は、あるクラスの生徒20人のハンドボール投げの記録をまとめたものである。この度数分布表から求められる記録の平均値を求めなさい。
【高校数学】数Ⅲ-116 関数の極値①

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(関数の極値①)
Q.次の関数の極値を求めよ
①$f(x)=\frac{x^2+2x+1}{x^2+1}$
➁$f(x)=x^2e^{-x}$
③$f(x)=\frac{\log x}{x^2}$
この動画を見る
数Ⅲ(関数の極値①)
Q.次の関数の極値を求めよ
①$f(x)=\frac{x^2+2x+1}{x^2+1}$
➁$f(x)=x^2e^{-x}$
③$f(x)=\frac{\log x}{x^2}$
韓国と中国(5問)【歴史64/さくっ答シリーズ】

単元:
#社会(中学生)#歴史
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
【歴史64/さくっ答シリーズ】韓国と中国
・1910年、日本は○○を併合し△△を設置して植民地支配をおし進めた。
・日本はポーツマス条約で得た鉄道の利権をもとに○○を設立して、満州での利権を独占していった
・中国では○○が中心となって、民族の独立を近代国家の建設を目指す革命運動が起こった
・孫文は○○主義という指導理論を唱えた
・1911年に○○革命が始まり、孫文を 臨時大総統とする△△が建国された
この動画を見る
【歴史64/さくっ答シリーズ】韓国と中国
・1910年、日本は○○を併合し△△を設置して植民地支配をおし進めた。
・日本はポーツマス条約で得た鉄道の利権をもとに○○を設立して、満州での利権を独占していった
・中国では○○が中心となって、民族の独立を近代国家の建設を目指す革命運動が起こった
・孫文は○○主義という指導理論を唱えた
・1911年に○○革命が始まり、孫文を 臨時大総統とする△△が建国された
【高校受験対策】数学-関数37(③)
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数37
Q.
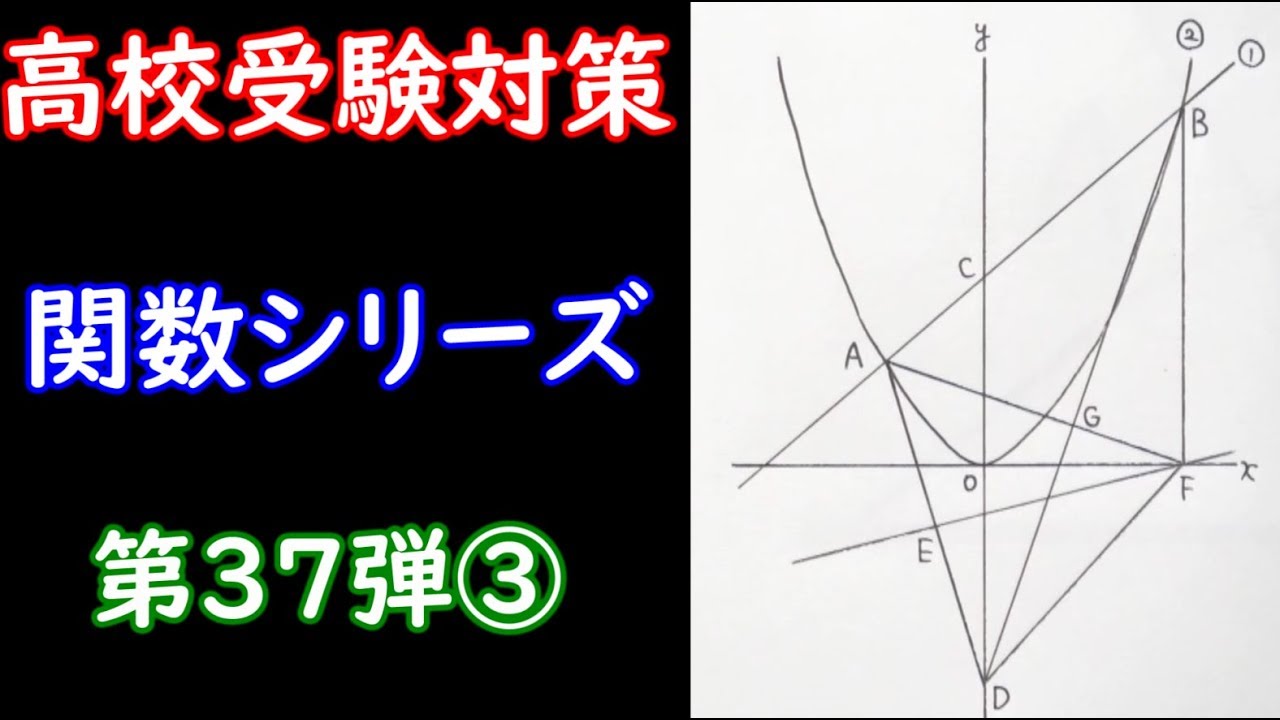
右の図において、直線①は関数$y=x+6$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 2点、A・Bはともに直線①と曲線②との交点で、点Aの$x$座標は$-3$、 点Bの$x$座標は$6$であり、点Cは直線①と$y$軸との交点である。
また、原点を$o$とするとき、点Dは$y$軸上の点で$CO:OD=6:7$であり、 その$y$座標は負である。
点Eは線分AD上の点でAE=EDである。 さらに点Fは$x$軸上の点で、線分BFは$y$軸に平行である。 このとき次の問いに答えなさい。
①曲線②の式$y=ax^2$の$a$の値を求めなさい。
➁直線EFの式を求めなさい。
③線分AFと線分BOとの交点をGとするとき、三角形AGBと三角形DFGの曲積の比を最も簡単な整数の比で表しなさい。
この動画を見る
高校受験対策・関数37
Q.
右の図において、直線①は関数$y=x+6$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 2点、A・Bはともに直線①と曲線②との交点で、点Aの$x$座標は$-3$、 点Bの$x$座標は$6$であり、点Cは直線①と$y$軸との交点である。
また、原点を$o$とするとき、点Dは$y$軸上の点で$CO:OD=6:7$であり、 その$y$座標は負である。
点Eは線分AD上の点でAE=EDである。 さらに点Fは$x$軸上の点で、線分BFは$y$軸に平行である。 このとき次の問いに答えなさい。
①曲線②の式$y=ax^2$の$a$の値を求めなさい。
➁直線EFの式を求めなさい。
③線分AFと線分BOとの交点をGとするとき、三角形AGBと三角形DFGの曲積の比を最も簡単な整数の比で表しなさい。
【高校受験対策】数学-図形22/後編

単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形22
Q.
右の図1のような、$\angle BAD \gt 90°$、$AB \gt AD$の平行四辺形$ABCD$があります。 点$E$は辺$CD$上の点で、$\angle BAE =\angle CDA$です。
このとき次の各問に答えなさい。
①$△ABEと△DCA$が合同であることを証明しなさい。
➁$\angle BAC = 40°$、$\angle DAE = 50°$のとき、$\angle CBE$、$\angle AEB$の大きさをそれぞれ求めなさい。
③
図2のように、図1において、線分$AE$の延長と辺$BC$の延長との交点を$F$とし、辺$AB$と線分$BF$をとなりあう2辺とする平行四辺形$ABFG$をつくります。点$E$を通り線分$BF$に平行な直線をひき、辺$AB$、線分$GF$との交点をそれぞれ$P,Q$とします。また、点$D$から線分$AE$に垂線をひき、その交点を$H$とします。
$△ACE$の面積が$30cm^2$ で、$DH=8cm$のとき、線分$EQ$の長さを求めなさい.
この動画を見る
高校受験対策・図形22
Q.
右の図1のような、$\angle BAD \gt 90°$、$AB \gt AD$の平行四辺形$ABCD$があります。 点$E$は辺$CD$上の点で、$\angle BAE =\angle CDA$です。
このとき次の各問に答えなさい。
①$△ABEと△DCA$が合同であることを証明しなさい。
➁$\angle BAC = 40°$、$\angle DAE = 50°$のとき、$\angle CBE$、$\angle AEB$の大きさをそれぞれ求めなさい。
③
図2のように、図1において、線分$AE$の延長と辺$BC$の延長との交点を$F$とし、辺$AB$と線分$BF$をとなりあう2辺とする平行四辺形$ABFG$をつくります。点$E$を通り線分$BF$に平行な直線をひき、辺$AB$、線分$GF$との交点をそれぞれ$P,Q$とします。また、点$D$から線分$AE$に垂線をひき、その交点を$H$とします。
$△ACE$の面積が$30cm^2$ で、$DH=8cm$のとき、線分$EQ$の長さを求めなさい.
【高校受験対策】数学-図形22/前編

単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形22
Q.
右の図1のような、$ \angle BAD \gt 90°$、$AB \gt AD$の平行四辺形$ABCD$があります。 点$E$は辺$CD$上の点で$\angle BAE= \angle CDA$です。
このとき次の各問に答えなさい。
①$△ABEと△DCA$が合同であることを証明しなさい。
➁$\angle BAC= 40°$、$\angle DAE= 50°$のとき、$\angle CBE$、$\angle AEB$の大きさをそれぞれ求めなさい。
③図2のように、図1において線分$AE$の延長と辺$BC$の延長との交点を$F$とし、辺$AB$と線分$BF$をとなりあう2辺とする平行四辺形$ABFG$を作ります。
点$E$を通り線分$BF$に平行な直線をひき、辺$AB$、線分$GF$との交点をそれぞれ$P,Q$とします。
また、点$D$から線分AEに垂線をひきその交点を$H$とます。
$△ACE$の面積が$30cm^2$で$DH=8cm$のとき、線分$EQ$の長さを求めなさい。
この動画を見る
高校受験対策・図形22
Q.
右の図1のような、$ \angle BAD \gt 90°$、$AB \gt AD$の平行四辺形$ABCD$があります。 点$E$は辺$CD$上の点で$\angle BAE= \angle CDA$です。
このとき次の各問に答えなさい。
①$△ABEと△DCA$が合同であることを証明しなさい。
➁$\angle BAC= 40°$、$\angle DAE= 50°$のとき、$\angle CBE$、$\angle AEB$の大きさをそれぞれ求めなさい。
③図2のように、図1において線分$AE$の延長と辺$BC$の延長との交点を$F$とし、辺$AB$と線分$BF$をとなりあう2辺とする平行四辺形$ABFG$を作ります。
点$E$を通り線分$BF$に平行な直線をひき、辺$AB$、線分$GF$との交点をそれぞれ$P,Q$とします。
また、点$D$から線分AEに垂線をひきその交点を$H$とます。
$△ACE$の面積が$30cm^2$で$DH=8cm$のとき、線分$EQ$の長さを求めなさい。
【高校受験対策】数学-死守33

単元:
#数学(中学生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守33
①$5-(-3)$
➁$6-5 \times (-2)$
③$4x-7x$
④$(2x+7y)-4(x-y)$
⑤$18a^3 \div\frac{2}{3}a$
⑥$\sqrt{75}-\sqrt{27}$
⑦$(2x+3)(2x-3)$を展開しなさい
⑧$x^2+6x-8$を因数分解しなさい
⑨2次方程式$(x-3)^2=2$を解きなさい
➉$y$は$x$に比例し、$x=3$のとき$y=-15$である。$y$を$x$の式で表しなさい。
⑪右の図の直角三角形ABCにおいて、辺ACの長さを求めなさい。
⑫大小2個のさいころを同時に投げるとき、出た目の和が8となる確率を求めなさい
⑬右の図の四角形ABCDと四角形EFGHは相似であり、その相似比は$2:3$である。
四角形ABCDの面積が$20cm^2$であるとき、四角形EFGHの面積を求めなさい。
⑭関数$y=ax^2$において、$x$の値が1から3まで増加するときの変化の割合が$2$であるとき、 $a$の値を求めなさい。
⑮右の図は、あるクラスの生徒20人について、1学期中に 読んだ本の冊数をヒストグラムにまとめたものである。
次のア~エのうち、この図から読み取れることとして正しいものを1つ選び、記号で答えなさい。
ア:生徒が読んだ冊数の範囲は5冊である
イ:生徒が読んだ冊数の最頻値は27.5冊である
ウ:度数が最も大きい階級の相対度数は0.3である
エ:度数が最も小さい階の階値は2.5冊である
この動画を見る
高校受験対策・死守33
①$5-(-3)$
➁$6-5 \times (-2)$
③$4x-7x$
④$(2x+7y)-4(x-y)$
⑤$18a^3 \div\frac{2}{3}a$
⑥$\sqrt{75}-\sqrt{27}$
⑦$(2x+3)(2x-3)$を展開しなさい
⑧$x^2+6x-8$を因数分解しなさい
⑨2次方程式$(x-3)^2=2$を解きなさい
➉$y$は$x$に比例し、$x=3$のとき$y=-15$である。$y$を$x$の式で表しなさい。
⑪右の図の直角三角形ABCにおいて、辺ACの長さを求めなさい。
⑫大小2個のさいころを同時に投げるとき、出た目の和が8となる確率を求めなさい
⑬右の図の四角形ABCDと四角形EFGHは相似であり、その相似比は$2:3$である。
四角形ABCDの面積が$20cm^2$であるとき、四角形EFGHの面積を求めなさい。
⑭関数$y=ax^2$において、$x$の値が1から3まで増加するときの変化の割合が$2$であるとき、 $a$の値を求めなさい。
⑮右の図は、あるクラスの生徒20人について、1学期中に 読んだ本の冊数をヒストグラムにまとめたものである。
次のア~エのうち、この図から読み取れることとして正しいものを1つ選び、記号で答えなさい。
ア:生徒が読んだ冊数の範囲は5冊である
イ:生徒が読んだ冊数の最頻値は27.5冊である
ウ:度数が最も大きい階級の相対度数は0.3である
エ:度数が最も小さい階の階値は2.5冊である
【時事問題】2018.10月前半

単元:
#社会(中学生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
時事問題(2018年10月前半)
・ 東京の築地市場に代わり、①市場の営業が始まった。
・早ければ2030年にも、世界の平均気温が②度上昇するといわれている。 そうなると2100年までに海水面が最大③cm上昇するといわれている。
・京都大学の④特別教授が⑤を授賞した。
・日本経済団体連合会は、大学生の⑥のルールを廃止すると発表した。
・第17回世界湖沼会議が⑦県で開かれた。
この動画を見る
時事問題(2018年10月前半)
・ 東京の築地市場に代わり、①市場の営業が始まった。
・早ければ2030年にも、世界の平均気温が②度上昇するといわれている。 そうなると2100年までに海水面が最大③cm上昇するといわれている。
・京都大学の④特別教授が⑤を授賞した。
・日本経済団体連合会は、大学生の⑥のルールを廃止すると発表した。
・第17回世界湖沼会議が⑦県で開かれた。


