 とある男が授業をしてみた
とある男が授業をしてみた
 とある男が授業をしてみた
とある男が授業をしてみた
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【高校数学】数Ⅲ-94 合成関数の微分法①

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数を微分せよ。
①$y=(x^2-5)^3$
②$y=(x^3+3x)^4$
③$y=(2x^3-3x+1)^5$
④$y=\dfrac{1}{(x^2-3)}^2$
⑤$y=\{(x-1)(x^2+4)\}^4$
この動画を見る
次の関数を微分せよ。
①$y=(x^2-5)^3$
②$y=(x^3+3x)^4$
③$y=(2x^3-3x+1)^5$
④$y=\dfrac{1}{(x^2-3)}^2$
⑤$y=\{(x-1)(x^2+4)\}^4$
【高校数学】数Ⅲ-93 商の微分法

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数を微分せよ。
①$y=\dfrac{2x}{x^2+1}$
②$y=\dfrac{1+x^2}{1-x^2}$
③$y=\dfrac{x^2+x^2-5x+2}{x^2}$
④$y=\dfrac{x^2-4x+3}{\sqrt x}$
この動画を見る
次の関数を微分せよ。
①$y=\dfrac{2x}{x^2+1}$
②$y=\dfrac{1+x^2}{1-x^2}$
③$y=\dfrac{x^2+x^2-5x+2}{x^2}$
④$y=\dfrac{x^2-4x+3}{\sqrt x}$
【高校数学】数Ⅲ-92 積の微分法

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数を微分せよ。
①$y=(x^2+2x)(x+3)$
②$y=(5x^2-3x-4)(2x+1)$
③$y=(x^2-3x+2)(x^2+1)$
④$y=(x+1)(x+2)(x+3)$
この動画を見る
次の関数を微分せよ。
①$y=(x^2+2x)(x+3)$
②$y=(5x^2-3x-4)(2x+1)$
③$y=(x^2-3x+2)(x^2+1)$
④$y=(x+1)(x+2)(x+3)$
【高校数学】数Ⅲ-91 微分(復習編)

単元:
#微分とその応用#微分法#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数を微分せよ。
①$y=x^4+x^3+x^2+x+1$
②$y=-2x^3+7x+4$
③$y=-\dfrac{3}{2}x^4+\dfrac{1}{3}x^3-5x$
④$y=(x^3-1)^2$
⑤関数$f(x)=\vert x(x-2) \vert $が$x=2$で
微分可能であるかどうかを調べよ。
この動画を見る
次の関数を微分せよ。
①$y=x^4+x^3+x^2+x+1$
②$y=-2x^3+7x+4$
③$y=-\dfrac{3}{2}x^4+\dfrac{1}{3}x^3-5x$
④$y=(x^3-1)^2$
⑤関数$f(x)=\vert x(x-2) \vert $が$x=2$で
微分可能であるかどうかを調べよ。
【高校数学】数Ⅲ-90 微分とは?

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
関数$f(x)$の①を求めることを微分という。
導関数の定義に従って、次の関数を微分せよ。
②$f(x)=\dfrac{2}{x}$
③$f(x)=\sqrt{x+2}$
この動画を見る
関数$f(x)$の①を求めることを微分という。
導関数の定義に従って、次の関数を微分せよ。
②$f(x)=\dfrac{2}{x}$
③$f(x)=\sqrt{x+2}$
【英語】中1-11 確認テスト②(be動詞編)

単元:
#英語(中学生)#中1英語#I am~. You are~.の文(肯定文・否定文・疑問文)#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)#He(She) is~. Who is~?の文(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
be動詞編の解説をしていきます。
この動画を見る
be動詞編の解説をしていきます。
【高校数学】数Ⅲ-89 中間値の定理

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①方程式$x + \log_2 x = 2$が$1\lt x\lt 2$に少なくとも
1つの実数解をもつことを示せ。
②方程式$x^4-5x+2=0$は、少なくとも1つの実数解をもつことを示せ。
この動画を見る
①方程式$x + \log_2 x = 2$が$1\lt x\lt 2$に少なくとも
1つの実数解をもつことを示せ。
②方程式$x^4-5x+2=0$は、少なくとも1つの実数解をもつことを示せ。
【英語】中1-9 教科と時間割

単元:
#英語(中学生)#中1英語#時刻の表し方とたずね方、曜日・日付のたずね方、When~?、「時」を表す前置詞
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英語での教科と時間割の表し方を解説していきます。
この動画を見る
英語での教科と時間割の表し方を解説していきます。
【英語】中1-8 曜日を覚えよう

単元:
#英語(中学生)#中1英語#時刻の表し方とたずね方、曜日・日付のたずね方、When~?、「時」を表す前置詞
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
曜日の覚え方に関して解説していきます。
この動画を見る
曜日の覚え方に関して解説していきます。
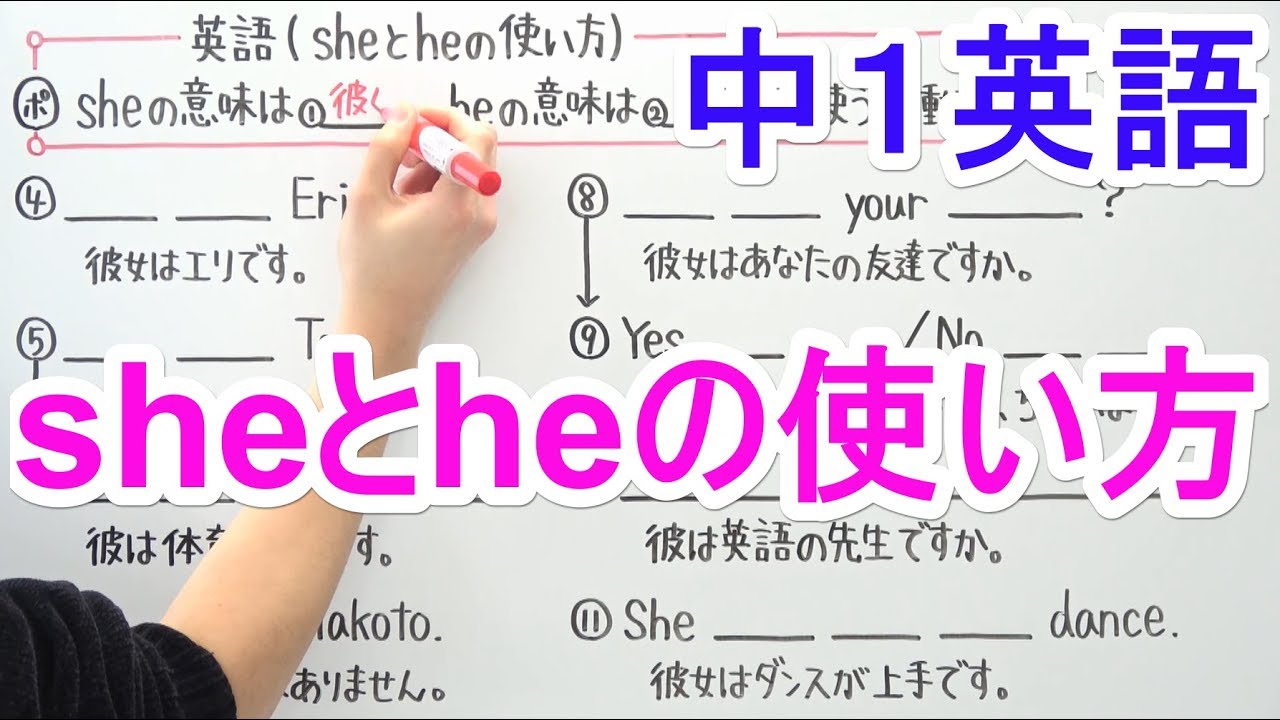
【英語】中1-7 sheとheの使い方
単元:
#英語(中学生)#中1英語#He(She) is~. Who is~?の文(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
sheとheの使い方を解説していきます。
この動画を見る
sheとheの使い方を解説していきます。
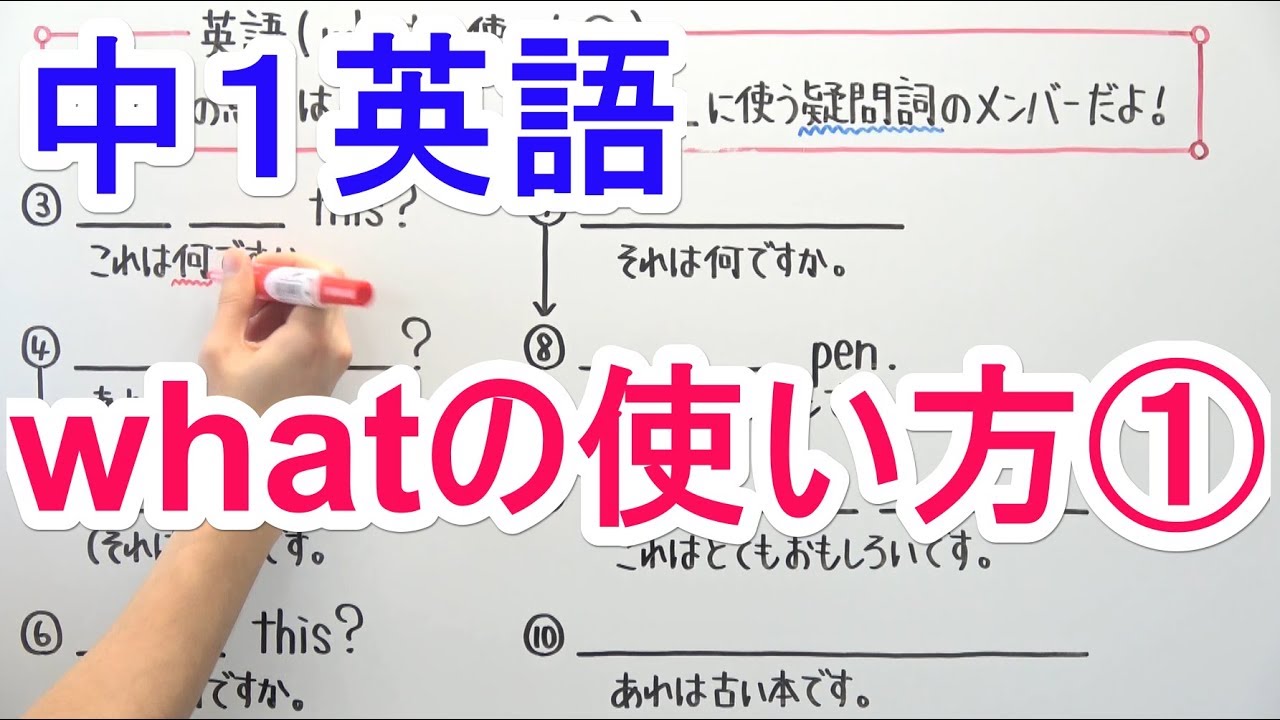
【英語】中1-6 whatの使い方①
単元:
#英語(中学生)#中1英語#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
whatの使い方①を解説していきます。
この動画を見る
whatの使い方①を解説していきます。
【高校数学】数Ⅲ-88 関数の連続性③

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①関数$f(x)=\lim_{n\to\infty}\dfrac{x^{2n+1}+1}{x^{2n}+1}$のグラフをかき、
$f(x)$が不連続となる$x$の値を求めよ。
この動画を見る
①関数$f(x)=\lim_{n\to\infty}\dfrac{x^{2n+1}+1}{x^{2n}+1}$のグラフをかき、
$f(x)$が不連続となる$x$の値を求めよ。
【英語】中1-5 確認テスト①(be動詞編)

単元:
#英語(中学生)#中1英語#I am~. You are~.の文(肯定文・否定文・疑問文)#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)#He(She) is~. Who is~?の文(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
be動詞に関して解説していきます。
この動画を見る
be動詞に関して解説していきます。
【高校数学】数Ⅲ-87 関数の連続性②

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数$f(x)$が、$x=0$で連続であるか不連続であるかを調べよ。
ただし、$[x]$は実数$x$を超えない最大の整数とする。
①$f(x)=3x^2$
②$f(x)=[\cos x]$
③$f(x)=x^2+\dfrac{x^2}{1+x^2}+\dfrac{x^2}{(1+x^2)^2}+・・・$
この動画を見る
次の関数$f(x)$が、$x=0$で連続であるか不連続であるかを調べよ。
ただし、$[x]$は実数$x$を超えない最大の整数とする。
①$f(x)=3x^2$
②$f(x)=[\cos x]$
③$f(x)=x^2+\dfrac{x^2}{1+x^2}+\dfrac{x^2}{(1+x^2)^2}+・・・$
【英語】中1-4 That isの使い方

単元:
#英語(中学生)#中1英語#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
That is~の使い方に関して解説します。
この動画を見る
That is~の使い方に関して解説します。
【高校数学】数Ⅲ-86 関数の連続性①

単元:
#関数と極限#微分とその応用#関数の極限#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
(1)次の不等式を満たす実数$x$の値の範囲を、区間で示す記号で示せ。
①$3\lt x \lt 7$
②$-2 \leqq x \leqq 0$
③$-4 \lt x \leqq 5$
④$x \geqq 12$
(2)次の関数が連続である区間を求めよ。
⑤$f(x)=\sqrt{-3x+2}$
⑥$f(x)=\dfrac{x^2+1}{x^2-3x+2}$
⑦$f(x)=\log_2 \vert x \vert$
この動画を見る
(1)次の不等式を満たす実数$x$の値の範囲を、区間で示す記号で示せ。
①$3\lt x \lt 7$
②$-2 \leqq x \leqq 0$
③$-4 \lt x \leqq 5$
④$x \geqq 12$
(2)次の関数が連続である区間を求めよ。
⑤$f(x)=\sqrt{-3x+2}$
⑥$f(x)=\dfrac{x^2+1}{x^2-3x+2}$
⑦$f(x)=\log_2 \vert x \vert$
【英語】中1-3 This isの使い方

単元:
#英語(中学生)#中1英語#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
This is~の使い方を解説していきます。
この動画を見る
This is~の使い方を解説していきます。
【高校数学】数Ⅲ-85 関数の決定問題

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$\displaystyle \lim_{x\to\infty} \dfrac{\sqrt{{x^2+2}-(ax+b)}}{x}=3$が成り立つように、
定数$a,b$の値を定めよ。
この動画を見る
①$\displaystyle \lim_{x\to\infty} \dfrac{\sqrt{{x^2+2}-(ax+b)}}{x}=3$が成り立つように、
定数$a,b$の値を定めよ。
【高校数学】数Ⅲ-84 三角関数と極限③

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty} \dfrac{\sin x}{x}$
②$\displaystyle \lim_{x\to 0} x^2 \sin \dfrac{1}{x}$
③$\displaystyle \lim_{x\to \infty} x \sin \dfrac{1}{x}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty} \dfrac{\sin x}{x}$
②$\displaystyle \lim_{x\to 0} x^2 \sin \dfrac{1}{x}$
③$\displaystyle \lim_{x\to \infty} x \sin \dfrac{1}{x}$
【高校数学】数Ⅲ-83 三角関数と極限②

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{x\to 0} \dfrac{1-\cos x}{x^2}$
②$\displaystyle \lim_{x\to \frac{\pi}{2}} \dfrac{\cos x}{2x-\pi}$
③$\displaystyle \lim_{x\to 0}\dfrac{\cos 3x-\cos 2x}{x^2}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to 0} \dfrac{1-\cos x}{x^2}$
②$\displaystyle \lim_{x\to \frac{\pi}{2}} \dfrac{\cos x}{2x-\pi}$
③$\displaystyle \lim_{x\to 0}\dfrac{\cos 3x-\cos 2x}{x^2}$
【高校数学】数Ⅲ-82 三角関数と極限①

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{x\to 0}\dfrac{\sin 3x}{x}$
②$\displaystyle \lim_{x\to 0}\dfrac{\tan 3x}{2x}$
③$\displaystyle \lim_{x\to 0}\dfrac{\tan 3x}{\sin 2x}$
④$\displaystyle \lim_{x\to 0}\dfrac{\sin x-\sin 5x}{2x}$
⑤$\displaystyle \lim_{x\to 0}\dfrac{1-\cos 2x}{x^2}$
⑥$\displaystyle \lim_{x\to 0}\dfrac{x\sin x}{1-\cos x}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to 0}\dfrac{\sin 3x}{x}$
②$\displaystyle \lim_{x\to 0}\dfrac{\tan 3x}{2x}$
③$\displaystyle \lim_{x\to 0}\dfrac{\tan 3x}{\sin 2x}$
④$\displaystyle \lim_{x\to 0}\dfrac{\sin x-\sin 5x}{2x}$
⑤$\displaystyle \lim_{x\to 0}\dfrac{1-\cos 2x}{x^2}$
⑥$\displaystyle \lim_{x\to 0}\dfrac{x\sin x}{1-\cos x}$
【高校数学】数Ⅲ-81 関数の極限⑥(対数関数)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty}\log_3 x$
②$\displaystyle \lim_{x\to \infty}\log_{\frac{1}{2}} x$
③$\displaystyle \lim_{x\to \infty}\log_{\frac{1}{2}}x$
④$\displaystyle \lim_{x\to \infty}\log_2 \dfrac{1}{2}$
⑤$\displaystyle \lim_{x\to \infty}\{\log_3 (x^2+1)-2\log_3 x\}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty}\log_3 x$
②$\displaystyle \lim_{x\to \infty}\log_{\frac{1}{2}} x$
③$\displaystyle \lim_{x\to \infty}\log_{\frac{1}{2}}x$
④$\displaystyle \lim_{x\to \infty}\log_2 \dfrac{1}{2}$
⑤$\displaystyle \lim_{x\to \infty}\{\log_3 (x^2+1)-2\log_3 x\}$
【高校数学】数Ⅲ-80 関数の極限⑤(指数関数)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty}(\sqrt 2)^x$
②$\displaystyle \lim_{x\to \infty}\left(\dfrac{1}{3}\right)^x$
③$\displaystyle \lim_{x\to \infty}2^{-x}$
④$\displaystyle \lim_{x\to \infty}\dfrac{5^x-7^x}{2^x+7^x}$
⑤$\displaystyle \lim_{x\to \infty}(2^x-3^x)$
⑥$\displaystyle \lim_{x\to \infty}(3^x-2^{2x+1})$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty}(\sqrt 2)^x$
②$\displaystyle \lim_{x\to \infty}\left(\dfrac{1}{3}\right)^x$
③$\displaystyle \lim_{x\to \infty}2^{-x}$
④$\displaystyle \lim_{x\to \infty}\dfrac{5^x-7^x}{2^x+7^x}$
⑤$\displaystyle \lim_{x\to \infty}(2^x-3^x)$
⑥$\displaystyle \lim_{x\to \infty}(3^x-2^{2x+1})$
【英語】中1-2 You areの使い方

単元:
#英語(中学生)#中1英語#I am~. You are~.の文(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
You areの使い方を解説していきます。
この動画を見る
You areの使い方を解説していきます。
【算数】小4-57 面と辺の垂直と平行

単元:
#算数(中学受験)#平面図形#平面図形その他
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
組み立てよう!
(図は動画内参照①~④)
完成した見取図を見て、あてはまるものをすべて書こう!
⑤面カに平行な面は?
⑥面ウに垂直な面は?
⑦辺ADに平行な辺は?
⑧点Aを通って、辺ABに垂直な辺は?
⑨面アに平行な辺は?
⑩面アに垂直な辺は?
この動画を見る
組み立てよう!
(図は動画内参照①~④)
完成した見取図を見て、あてはまるものをすべて書こう!
⑤面カに平行な面は?
⑥面ウに垂直な面は?
⑦辺ADに平行な辺は?
⑧点Aを通って、辺ABに垂直な辺は?
⑨面アに平行な辺は?
⑩面アに垂直な辺は?
【英語】中1-1 I amの使い方

単元:
#英語(中学生)#中1英語#I am~. You are~.の文(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
i amの使い方を解説していきます。
この動画を見る
i amの使い方を解説していきます。
【英語】中1-0.9 英語のルールを覚えよう

単元:
#英語(中学生)#中1英語#名詞・代名詞の複数形、How many~?、someとany
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\boxed{1}$文の①は大文字でかく。Hello, everyone.
,は② .は③という意味である。
$\boxed{2}$固有名詞の最初は④でかく。
Tom、Kumi、America. Tokyo
$\boxed{3}$⑤の順番でかき始める。
I am Yuki. I play soccer.
$\boxed{4}$疑問文………⑥ する文で、⑦で終わる。
否定文・・・「~ではありません」という文で、⑧を使う。
この動画を見る
$\boxed{1}$文の①は大文字でかく。Hello, everyone.
,は② .は③という意味である。
$\boxed{2}$固有名詞の最初は④でかく。
Tom、Kumi、America. Tokyo
$\boxed{3}$⑤の順番でかき始める。
I am Yuki. I play soccer.
$\boxed{4}$疑問文………⑥ する文で、⑦で終わる。
否定文・・・「~ではありません」という文で、⑧を使う。
【高校数学】数Ⅲ-79 関数の極限④

単元:
#関数と極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty}(3x^2-5x+2)$
②$\displaystyle \lim_{x\to \infty}\dfrac{5x+4}{x^2+3x-1}$
③$\displaystyle \lim_{x\to \infty}\dfrac{2x^2-1}{3x^2-4x+2}$
④$\displaystyle \lim_{x\to \infty}\dfrac{x^2+3x}{x-2}$
⑤$\displaystyle \lim_{x\to \infty}(\sqrt{x^2+3x-1}+x)$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty}(3x^2-5x+2)$
②$\displaystyle \lim_{x\to \infty}\dfrac{5x+4}{x^2+3x-1}$
③$\displaystyle \lim_{x\to \infty}\dfrac{2x^2-1}{3x^2-4x+2}$
④$\displaystyle \lim_{x\to \infty}\dfrac{x^2+3x}{x-2}$
⑤$\displaystyle \lim_{x\to \infty}(\sqrt{x^2+3x-1}+x)$
【高校数学】数Ⅲ-78 関数の極限③(右側左側)

単元:
#関数と極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{x\to -0}\dfrac{\vert x \vert}{x}$
②$\displaystyle \lim_{x\to 3+0}\dfrac{x^2-3x}{\vert x-3 \vert}$
③$\displaystyle \lim_{x\to 1-0}\dfrac{\vert x-1\vert}{x^3-1}$
④$x\to 0$のときの$\dfrac{x}{\vert x\vert}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to -0}\dfrac{\vert x \vert}{x}$
②$\displaystyle \lim_{x\to 3+0}\dfrac{x^2-3x}{\vert x-3 \vert}$
③$\displaystyle \lim_{x\to 1-0}\dfrac{\vert x-1\vert}{x^3-1}$
④$x\to 0$のときの$\dfrac{x}{\vert x\vert}$
【高校数学】数Ⅲ-77 関数の極限②

単元:
#関数と極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の等式が成り立つように、定数$a,b$の値を定めよ。
①$\displaystyle \lim_{n\to 2}\dfrac{x^2+ax+b}{x+2}=3$
②$\displaystyle \lim_{x\to 3}\dfrac{\sqrt{3x+a}-b}{x-3}=\dfrac{3}{8}$
この動画を見る
次の等式が成り立つように、定数$a,b$の値を定めよ。
①$\displaystyle \lim_{n\to 2}\dfrac{x^2+ax+b}{x+2}=3$
②$\displaystyle \lim_{x\to 3}\dfrac{\sqrt{3x+a}-b}{x-3}=\dfrac{3}{8}$


