 とある男が授業をしてみた
とある男が授業をしてみた
 とある男が授業をしてみた
とある男が授業をしてみた
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【高校数学】数Ⅲ-48 極座標と極方程式⑤

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の直交座標を用いて表された曲線を、極方程式で表せ。
①$\sqrt3x-y-4=0$
②$x^2-y^2=-4$
③$x^2+y^2=-2x$
この動画を見る
次の直交座標を用いて表された曲線を、極方程式で表せ。
①$\sqrt3x-y-4=0$
②$x^2-y^2=-4$
③$x^2+y^2=-2x$
【テスト対策・中3】4章-8

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように、放物線$y=ax^2$と直線が点$A(4,-8)$と点$B$で交わり、
点$B$の$y$座標は-2である。
$y$軸上に点$P(0,P)$があるとき、次の問いに答えなさい。
ただし、$P \lt 0$とする。
①$a$の値を求めなさい。
②直線$AB$の式を求めなさい。
③$△OAB$と$△ABP$の面積比が$1:3$となるとき、
$P$の値を求めなさい。
④$△OAB$と$△ABP$の面積比が$2:5$となるとき、
$P$の値を求めなさい。
図は動画内参照
この動画を見る
右の図のように、放物線$y=ax^2$と直線が点$A(4,-8)$と点$B$で交わり、
点$B$の$y$座標は-2である。
$y$軸上に点$P(0,P)$があるとき、次の問いに答えなさい。
ただし、$P \lt 0$とする。
①$a$の値を求めなさい。
②直線$AB$の式を求めなさい。
③$△OAB$と$△ABP$の面積比が$1:3$となるとき、
$P$の値を求めなさい。
④$△OAB$と$△ABP$の面積比が$2:5$となるとき、
$P$の値を求めなさい。
図は動画内参照
【テスト対策・中3】4章-7

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように、関数$y=\dfrac{1}{2}x^2$のグラフ上に2点$A,B$があり、
それぞれの$x$座標は$-2,4$である。
直線$AB$と$y$軸との交点を$C$とするとき、次の問いに答えなさい。
①$△AOB$の面積を求めなさい。
②原点$O$を通り、$△AOB$の面積を2等分する直線の式を求めなさい。
③点$A$を通り、$△AOB$の面積を2等分する直線の式を求めなさい。
図は動画内参照
この動画を見る
右の図のように、関数$y=\dfrac{1}{2}x^2$のグラフ上に2点$A,B$があり、
それぞれの$x$座標は$-2,4$である。
直線$AB$と$y$軸との交点を$C$とするとき、次の問いに答えなさい。
①$△AOB$の面積を求めなさい。
②原点$O$を通り、$△AOB$の面積を2等分する直線の式を求めなさい。
③点$A$を通り、$△AOB$の面積を2等分する直線の式を求めなさい。
図は動画内参照
【テスト対策・中3】4章-6

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右図のように、関数$y=x^2$のグラフ上に3点$A、B、C$があり、
$y$軸上に点$D$がある。
四角形$ABCD$が平行四辺形となるとき、次の問いに答えなさい。
①$A(- 1, 1), B(2, 4), D(0, 6)$のとき、点$c$の座標を求めなさい。
②$A(- 1, 1), D(0, 8)$のとき、四角形$ABCD$の面積を求めなさい。
図は動画内参照
この動画を見る
右図のように、関数$y=x^2$のグラフ上に3点$A、B、C$があり、
$y$軸上に点$D$がある。
四角形$ABCD$が平行四辺形となるとき、次の問いに答えなさい。
①$A(- 1, 1), B(2, 4), D(0, 6)$のとき、点$c$の座標を求めなさい。
②$A(- 1, 1), D(0, 8)$のとき、四角形$ABCD$の面積を求めなさい。
図は動画内参照
【テスト対策・中3】4章-5

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右図のように、関数$ y=\dfrac{1}{2}x^2$のグラフ上に2点$A(0,18),B(2,2)$がある。
次の問いに答えなさい。ただし、$ a \lt 0$とする。
①$a$の値を求めなさい。
②直線$AB$の式を求めなさい。
③$△OAB$の面積を求めなさい。
④$x$軸上に点$Q$をとる。
$AQ+BQ$の長さが最短となるときの点$Q$の座標を求めなさい。
図は動画内参照
この動画を見る
右図のように、関数$ y=\dfrac{1}{2}x^2$のグラフ上に2点$A(0,18),B(2,2)$がある。
次の問いに答えなさい。ただし、$ a \lt 0$とする。
①$a$の値を求めなさい。
②直線$AB$の式を求めなさい。
③$△OAB$の面積を求めなさい。
④$x$軸上に点$Q$をとる。
$AQ+BQ$の長さが最短となるときの点$Q$の座標を求めなさい。
図は動画内参照
【テスト対策・中3】4章-4

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
点$(-2,-2)$を通り、傾き2の直線を$\ell$とし、
$\ell$が関数$y = x ^ 2$と交わる2点を$P、Q$とする。
右の図のように、$P、Q$から$x$軸に下ろした垂線をそれぞれ$PA、QB$とするとき、
次の問いに答えなさい。
①直線の式を求めなさい。
②線分$AB$の長さを求めなさい。
③四角形$ABQP$の面積を求めなさい。
図は動画内参照
この動画を見る
点$(-2,-2)$を通り、傾き2の直線を$\ell$とし、
$\ell$が関数$y = x ^ 2$と交わる2点を$P、Q$とする。
右の図のように、$P、Q$から$x$軸に下ろした垂線をそれぞれ$PA、QB$とするとき、
次の問いに答えなさい。
①直線の式を求めなさい。
②線分$AB$の長さを求めなさい。
③四角形$ABQP$の面積を求めなさい。
図は動画内参照
【テスト対策・中3】4章-3

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①関数$y=ax^2$について、$x$の変域が$-3≦x≦2$のとき、
$y$の変域は$0\leqq y \leqq 6$である。 このとき、$a$の値を求めなさい。
②関数$y=\dfrac{1}{3}x^2$で、$x$の変域を$a≦x≦3$とすると、
その変域は$b\leqq y\leqq 12$となる。$a、b$の値を求めなさい。
③関数$y=-\dfrac{1}{4}x^2$について、$x$の変域が$a≦y≦a+5$であるとき、
$y$の変域が$-4≦y\leqq 0$となるような$a$の値をすべて求めなさい。
この動画を見る
①関数$y=ax^2$について、$x$の変域が$-3≦x≦2$のとき、
$y$の変域は$0\leqq y \leqq 6$である。 このとき、$a$の値を求めなさい。
②関数$y=\dfrac{1}{3}x^2$で、$x$の変域を$a≦x≦3$とすると、
その変域は$b\leqq y\leqq 12$となる。$a、b$の値を求めなさい。
③関数$y=-\dfrac{1}{4}x^2$について、$x$の変域が$a≦y≦a+5$であるとき、
$y$の変域が$-4≦y\leqq 0$となるような$a$の値をすべて求めなさい。
【テスト対策・中3】4章-2

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右のア~エの関数について、下の問いに記号で答えなさい。
①$y$の値が、$x=0$のとき最大になるものをすべて選びなさい。
②$x\geqq 0$の範囲で、$x$の値が増加するにつれて、
$y$の値が減少するものをすべて選びなさい。
ア.$y=-3x^2$
イ.$y=x^2$
ウ.$y=4x^2$
エ.$y=-\dfrac{2}{3}x^2$
③$x$の変域を$-2\leqq x \leqq 1$とするとき、
関数$y-3x^2$と$y$の変域が同じになる関数を
次のア~エから一つ選び、記号で答えなさい。
ア.$y=-4x+8$
イ.$y=-3x^2$
ウ.$y=4x+8$
エ.$y=3x-3$
この動画を見る
右のア~エの関数について、下の問いに記号で答えなさい。
①$y$の値が、$x=0$のとき最大になるものをすべて選びなさい。
②$x\geqq 0$の範囲で、$x$の値が増加するにつれて、
$y$の値が減少するものをすべて選びなさい。
ア.$y=-3x^2$
イ.$y=x^2$
ウ.$y=4x^2$
エ.$y=-\dfrac{2}{3}x^2$
③$x$の変域を$-2\leqq x \leqq 1$とするとき、
関数$y-3x^2$と$y$の変域が同じになる関数を
次のア~エから一つ選び、記号で答えなさい。
ア.$y=-4x+8$
イ.$y=-3x^2$
ウ.$y=4x+8$
エ.$y=3x-3$
【テスト対策・中3】4章-1

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$y=ax^2$について、$ x = 2$のとき$y=-3$である。
このとき、$a$の値を求めなさい。
②$y$は$x$の2乗に比例し、$x=-6$のとき$y = 9$である。
$x = 12$のときの$y$の値を求めなさい。
③右図において、$m$は$y=ax^2$($a$は定数)のグラフで、
$A(3,-4)$は$m$上にある。
このとき、$a$の値を求めなさい。
図は動画内参照
この動画を見る
①$y=ax^2$について、$ x = 2$のとき$y=-3$である。
このとき、$a$の値を求めなさい。
②$y$は$x$の2乗に比例し、$x=-6$のとき$y = 9$である。
$x = 12$のときの$y$の値を求めなさい。
③右図において、$m$は$y=ax^2$($a$は定数)のグラフで、
$A(3,-4)$は$m$上にある。
このとき、$a$の値を求めなさい。
図は動画内参照
【テスト対策・中1】3章-3

単元:
#数学(中学生)#中1数学#比例・反比例
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の比例式を解きなさい。
①$x:12=5:4$
②$9:x=2:\dfrac{4}{3}$
③$(x-4):3=(x-8):2$
比例式$16:x=22:\Box$について、$\Box$にあてはまる数は
$x$の値よりも3大きい。
このとき、$\Box$にあてはまる数を求めなさい。
この動画を見る
次の比例式を解きなさい。
①$x:12=5:4$
②$9:x=2:\dfrac{4}{3}$
③$(x-4):3=(x-8):2$
比例式$16:x=22:\Box$について、$\Box$にあてはまる数は
$x$の値よりも3大きい。
このとき、$\Box$にあてはまる数を求めなさい。
【テスト対策・中1】3章-2

単元:
#数学(中学生)#中1数学#方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の方程式の解き方はまちがっている。
ア~エで、最初にまちがえた式を選び、記号で答えなさい。
また、正しい解を求めなさい。
①$x-1=3(3+x)$
$x-1=9+3x$・・・ア
$x-3x=0-1$・・・イ
$-2x=8$・・・ウ
$x=-4$・・・エ
②$\dfrac{x}{4}-1=\dfrac{x-2}{3}$
$3x-12=4x-2$・・・ア
$3x-4x=-2+12$・・・イ
$-x=10$・・・ウ
$x=-10$・・・エ
この動画を見る
次の方程式の解き方はまちがっている。
ア~エで、最初にまちがえた式を選び、記号で答えなさい。
また、正しい解を求めなさい。
①$x-1=3(3+x)$
$x-1=9+3x$・・・ア
$x-3x=0-1$・・・イ
$-2x=8$・・・ウ
$x=-4$・・・エ
②$\dfrac{x}{4}-1=\dfrac{x-2}{3}$
$3x-12=4x-2$・・・ア
$3x-4x=-2+12$・・・イ
$-x=10$・・・ウ
$x=-10$・・・エ
【テスト対策・中1】3章-1

単元:
#数学(中学生)#中1数学#方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の方程式を解きなさい。
①$5x-2=3x+4$
②$13=6-(2x-5)$
③$3(3x-2)=-3(5-x)$
④$\dfrac{1}{3}x+4=2+x$
⑤$\dfrac{x-1}{2}-2=\dfrac{2x-1}{3}$
⑥$0.1(x+1)=0.06(x+15)$
この動画を見る
次の方程式を解きなさい。
①$5x-2=3x+4$
②$13=6-(2x-5)$
③$3(3x-2)=-3(5-x)$
④$\dfrac{1}{3}x+4=2+x$
⑤$\dfrac{x-1}{2}-2=\dfrac{2x-1}{3}$
⑥$0.1(x+1)=0.06(x+15)$
【テスト対策・中2】3章-5
単元:
#数学(中学生)#中2数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
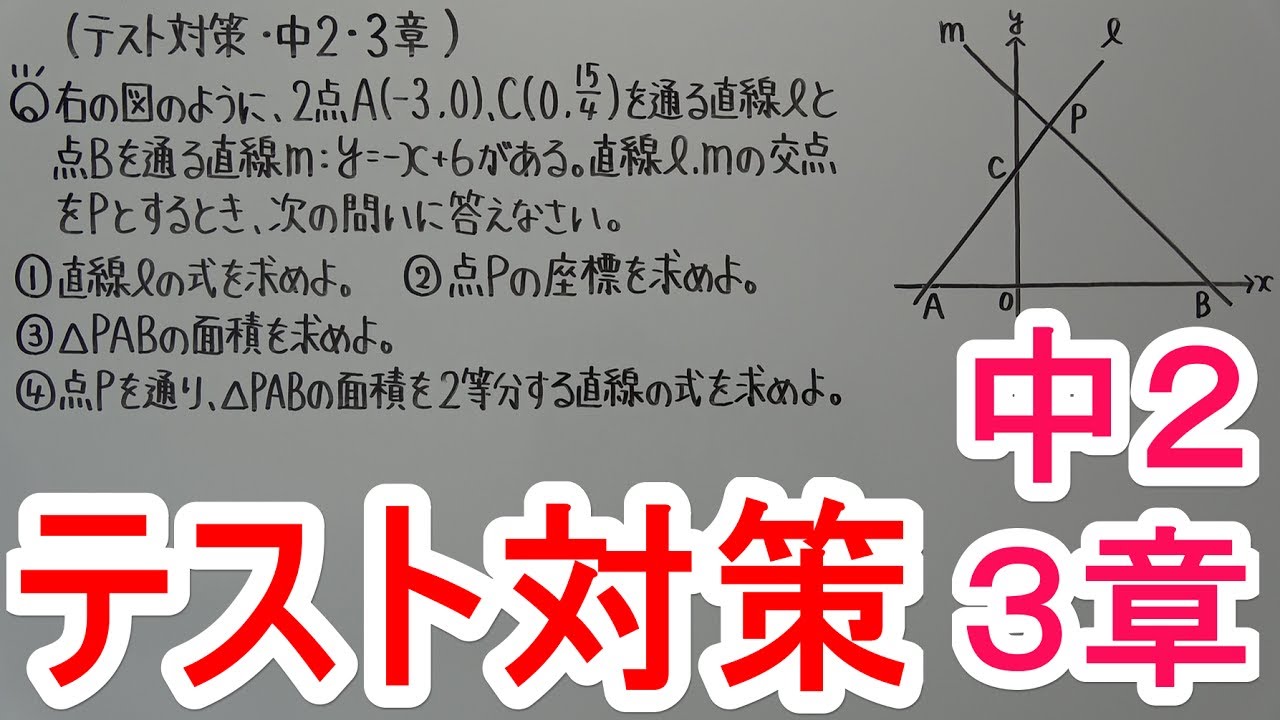
右の図のように、2点$A(-3,0)、C\left(0,\dfrac{15}{4}\right)$を通る直線$\ell$と
点$B$を通る直線$m:y = - x + 6$がある。
直線$\ell.m$の交点を$P$とするとき、次の問いに答えなさい。
①直線$\ell$の式を求めよ。
②点$P$の座標を求めよ。
③$△PAB$の面積を求めよ。
④点$P$を通り、$△PAB$の面積を2等分する直線の式を求めよ。
図は動画内参照
この動画を見る
右の図のように、2点$A(-3,0)、C\left(0,\dfrac{15}{4}\right)$を通る直線$\ell$と
点$B$を通る直線$m:y = - x + 6$がある。
直線$\ell.m$の交点を$P$とするとき、次の問いに答えなさい。
①直線$\ell$の式を求めよ。
②点$P$の座標を求めよ。
③$△PAB$の面積を求めよ。
④点$P$を通り、$△PAB$の面積を2等分する直線の式を求めよ。
図は動画内参照
【テスト対策・中2】3章-4

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図で、 $A(4,5), B(5,0)$で、点$C$を通る直線の式を$y = ax - 2$とする。
この直線が線分$AB$(両端の点$A、B$を含む)と交わるとき、
$a$の値の範囲を求めなさい。
②直線$y = -\dfrac{2}{3}x+\dfrac{17}{3}$上にある、
$x$標、$y$座標がともに正の整数である点の座標をすべて求めなさい。
図は動画内参照
この動画を見る
①右の図で、 $A(4,5), B(5,0)$で、点$C$を通る直線の式を$y = ax - 2$とする。
この直線が線分$AB$(両端の点$A、B$を含む)と交わるとき、
$a$の値の範囲を求めなさい。
②直線$y = -\dfrac{2}{3}x+\dfrac{17}{3}$上にある、
$x$標、$y$座標がともに正の整数である点の座標をすべて求めなさい。
図は動画内参照
【高校数学】数Ⅲ-47 極座標と極方程式④

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$O$を極とする次の極方程式を直交座標で表される方程式に直せ。
①$r=\dfrac{1}{2\cos\theta-\sin\theta}$
②$r=\dfrac{2}{1-\sqrt2\cos\theta}$
③$r=\dfrac{2}{1-\cos\theta}$
この動画を見る
$O$を極とする次の極方程式を直交座標で表される方程式に直せ。
①$r=\dfrac{1}{2\cos\theta-\sin\theta}$
②$r=\dfrac{2}{1-\sqrt2\cos\theta}$
③$r=\dfrac{2}{1-\cos\theta}$
【テスト対策・中2】3章-3

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図のように、2点$A(1,3)、B(4,1)$がある。
$y$軸上に点$P$をとり、$AP+PB$の長さを考える。
$AP+PB$の長さが最も短くなるとき、点$P$の座標を求めなさい。
図は動画内参照
この動画を見る
①右の図のように、2点$A(1,3)、B(4,1)$がある。
$y$軸上に点$P$をとり、$AP+PB$の長さを考える。
$AP+PB$の長さが最も短くなるとき、点$P$の座標を求めなさい。
図は動画内参照
【高校数学】数Ⅲ-46 極座標と極方程式③

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$O$を極とする極座標において、
2点$A\left(2,\dfrac{\pi}{6}\right),B\left(4,\dfrac{5}{6}\pi\right)$がある。
①線分$AB$の長さを求めよ。
②$\triangle OAB$の面積を求めよ。
この動画を見る
$O$を極とする極座標において、
2点$A\left(2,\dfrac{\pi}{6}\right),B\left(4,\dfrac{5}{6}\pi\right)$がある。
①線分$AB$の長さを求めよ。
②$\triangle OAB$の面積を求めよ。
【テスト対策・中2】3章-2

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の1次関数の式を求めなさい。
①2点$(-2,5)、(1、-4)$を通る直線
②変化の割合が$5$で、$x=2$のとき$y=6$となる直線
③$x$軸に平行で、点$(-2,3)$を通る直線
④2直線$y=3x+6、y=-2x+1$の交点を通り、$y=\dfrac{1}{3}x-2$と平行な直線
この動画を見る
次の1次関数の式を求めなさい。
①2点$(-2,5)、(1、-4)$を通る直線
②変化の割合が$5$で、$x=2$のとき$y=6$となる直線
③$x$軸に平行で、点$(-2,3)$を通る直線
④2直線$y=3x+6、y=-2x+1$の交点を通り、$y=\dfrac{1}{3}x-2$と平行な直線
【高校数学】数Ⅲ-45 極座標と極方程式②

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極座標の点$A,B$の直交座標を求めよ。
①$A\left(3,\dfrac{\pi}{6}\right)$
②$B\left(2,-\dfrac{5}{6}\pi\right)$
次の直交座標の点$C,D$の極座標$(r,\theta)$を求めよ。
ただし、$0\leqq \theta \leqq 2\pi$とする。
③$C(0,-2)$
④$D(\sqrt3,-3)$
この動画を見る
次の極座標の点$A,B$の直交座標を求めよ。
①$A\left(3,\dfrac{\pi}{6}\right)$
②$B\left(2,-\dfrac{5}{6}\pi\right)$
次の直交座標の点$C,D$の極座標$(r,\theta)$を求めよ。
ただし、$0\leqq \theta \leqq 2\pi$とする。
③$C(0,-2)$
④$D(\sqrt3,-3)$
【テスト対策・中2】3章-1

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①1次関数$y=-\dfrac{3}{2}x+\dfrac{1}{5}$について、
$x$の増加量が10のときの$y$の増加量を求めなさい。
②1次関数$y=-x-6$で、$x$の変域が$-3\leqq x \leqq 2$のとき、
$y$の変域を求めなさい。
③直線$3x-2y=12$と$x$軸との交点を、
直線$ax-y=-8$が通るとき、$a$の値を求めなさい。
この動画を見る
①1次関数$y=-\dfrac{3}{2}x+\dfrac{1}{5}$について、
$x$の増加量が10のときの$y$の増加量を求めなさい。
②1次関数$y=-x-6$で、$x$の変域が$-3\leqq x \leqq 2$のとき、
$y$の変域を求めなさい。
③直線$3x-2y=12$と$x$軸との交点を、
直線$ax-y=-8$が通るとき、$a$の値を求めなさい。
【高校数学】数Ⅲ-44 極座標と極方程式①

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右図において$(r、0)$を点$P$の極座標といい、
点$O$を①、半直線$OX$を②、角$\theta$を③という。
極座標に対して、$x、y$座標の組$(x,y)$を④座標といい、
x= ⑤、y=⑥、$r = \sqrt{x ^ 2 + y ^ 2}$が成り立つ。
平面上の曲線が、極座標$(r,\theta)$を用いた式$r=f(\theta)$または
$F(r,\theta)=0$で表されるとき、この方程式を曲線の極方程式という。
中心が極$O$、半径が$a$の円→⑦
中心が$(a,0)$、半径が$a$の円→⑧
極$O$を通り、始線となす角が$\beta$の直線→⑨
図は動画内参照
この動画を見る
右図において$(r、0)$を点$P$の極座標といい、
点$O$を①、半直線$OX$を②、角$\theta$を③という。
極座標に対して、$x、y$座標の組$(x,y)$を④座標といい、
x= ⑤、y=⑥、$r = \sqrt{x ^ 2 + y ^ 2}$が成り立つ。
平面上の曲線が、極座標$(r,\theta)$を用いた式$r=f(\theta)$または
$F(r,\theta)=0$で表されるとき、この方程式を曲線の極方程式という。
中心が極$O$、半径が$a$の円→⑦
中心が$(a,0)$、半径が$a$の円→⑧
極$O$を通り、始線となす角が$\beta$の直線→⑨
図は動画内参照
【高校数学】数Ⅲ-43 曲線の媒介変数表示④

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$x、y$が$\dfrac{x^2}{2}+\dfrac{y^2}{8}=1$を満たす実数のとき、
$2x^2+xy+y^2$の最大値、最小値を求めよ。
この動画を見る
①$x、y$が$\dfrac{x^2}{2}+\dfrac{y^2}{8}=1$を満たす実数のとき、
$2x^2+xy+y^2$の最大値、最小値を求めよ。
【高校数学】数Ⅲ-42 曲線の媒介変数表示③

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$t$を媒介変数とする。
次の式で表される図形はどのような曲線か。
①$x=\dfrac{1}{1+t^2}、y=\dfrac{t}{1+t^2}$
②$x=t+\dfrac{1}{t}、y=t-\dfrac{1}{t} \quad (t \gt 0)$
この動画を見る
$t$を媒介変数とする。
次の式で表される図形はどのような曲線か。
①$x=\dfrac{1}{1+t^2}、y=\dfrac{t}{1+t^2}$
②$x=t+\dfrac{1}{t}、y=t-\dfrac{1}{t} \quad (t \gt 0)$
【高校数学】数Ⅲ-41 曲線の媒介変数表示②

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\theta$を媒介変数とする。次の式で表される図形はどのような曲線か。
①$\begin{eqnarray}
\left\{
\begin{array}{l}
x=3\cos\theta-2 \\
y=5\sin\theta+2
\end{array}
\right.
\end{eqnarray}$
②$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\dfrac{3}{\cos\theta}+5\\
y=2\tan\theta-1
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\theta$を媒介変数とする。次の式で表される図形はどのような曲線か。
①$\begin{eqnarray}
\left\{
\begin{array}{l}
x=3\cos\theta-2 \\
y=5\sin\theta+2
\end{array}
\right.
\end{eqnarray}$
②$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\dfrac{3}{\cos\theta}+5\\
y=2\tan\theta-1
\end{array}
\right.
\end{eqnarray}$
【テスト対策・中3】3章-7

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①2次方程式$(x-3)^2=12$の2つの解を、$m、n$とするとき、
$\dfrac{(m+n)^2}{mn}$の値を求めなさい。
②2次方程式$x^2-16x+3a=0$の解がともに奇数となるような
正の整数$a$の値をすべて求めなさい。
この動画を見る
①2次方程式$(x-3)^2=12$の2つの解を、$m、n$とするとき、
$\dfrac{(m+n)^2}{mn}$の値を求めなさい。
②2次方程式$x^2-16x+3a=0$の解がともに奇数となるような
正の整数$a$の値をすべて求めなさい。
【テスト対策・中3】3章-6

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
① 右の図のように、$BC=6cm、CA=7cm、∠BCA=90°$の$△ABC$がある。
辺$BC$上に2点$P、Q$を、辺$CA$上に点$R$を$BP=QC=RA$となるようにとる。
$△ABP$と$△RQC$の面積の和が$△ABC$の面積の$\dfrac{4}{7}$となるとき、
$BP$の長さを求めなさい。ただし、$0\lt BP\lt 3$とする。
図は動画内参照
この動画を見る
① 右の図のように、$BC=6cm、CA=7cm、∠BCA=90°$の$△ABC$がある。
辺$BC$上に2点$P、Q$を、辺$CA$上に点$R$を$BP=QC=RA$となるようにとる。
$△ABP$と$△RQC$の面積の和が$△ABC$の面積の$\dfrac{4}{7}$となるとき、
$BP$の長さを求めなさい。ただし、$0\lt BP\lt 3$とする。
図は動画内参照
【テスト対策・中3】3章-5

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の方程式を解きなさい.
①$3x^2-36x+48-0$
②$-\dfrac{2}{3}x^2+4x=0$
③$(x-3)(x+2)=1$
④$2(x^2-4)=(x-2)(x+6)$
⑤$(6x-7)^2-17(6x-7)=60$
この動画を見る
次の方程式を解きなさい.
①$3x^2-36x+48-0$
②$-\dfrac{2}{3}x^2+4x=0$
③$(x-3)(x+2)=1$
④$2(x^2-4)=(x-2)(x+6)$
⑤$(6x-7)^2-17(6x-7)=60$
【テスト対策・中3】3章-4

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①2次方程式$x^2+ax-21=0$の解の1つが-3のとき,
$a$の値ともう一つの解を求めなさい.
②2つの数5,-2を解にもつ2次方程式のうち,
$x^2$の係数が1であるものを求めなさい.
③2次方程式$x^2+ax+b=0$の解が2.3のとき,
2次方程式$x^2+bx+a=0$を解きなさい.
この動画を見る
①2次方程式$x^2+ax-21=0$の解の1つが-3のとき,
$a$の値ともう一つの解を求めなさい.
②2つの数5,-2を解にもつ2次方程式のうち,
$x^2$の係数が1であるものを求めなさい.
③2次方程式$x^2+ax+b=0$の解が2.3のとき,
2次方程式$x^2+bx+a=0$を解きなさい.
【高校数学】数Ⅲ-40 曲線の媒介変数表示①

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の曲線を,角$\theta$を媒介変数として表せ.
①$9x^2+y^2=16$
②$x^2+y^2=16$
③$4x^2-9y^2=36$
この動画を見る
次の曲線を,角$\theta$を媒介変数として表せ.
①$9x^2+y^2=16$
②$x^2+y^2=16$
③$4x^2-9y^2=36$
【テスト対策・中3】3章-3(たすきがけ)

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の方程式を解きなさい.
①$3x^2-5x-2=0$
②$3x^2-10x-8=0$
③$10x^2-13x-3=0$
④$-6x^2-11x+2=0$
この動画を見る
次の方程式を解きなさい.
①$3x^2-5x-2=0$
②$3x^2-10x-8=0$
③$10x^2-13x-3=0$
④$-6x^2-11x+2=0$


