 とある男が授業をしてみた
とある男が授業をしてみた
 とある男が授業をしてみた
とある男が授業をしてみた
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【きっかけ英単語-27】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①water
②doctor
③war
④willing
⑤especially
⑥tall
⑦age
⑧customer
⑨everywhere
⑩direction
この動画を見る
英単語を解説していきます.
①water
②doctor
③war
④willing
⑤especially
⑥tall
⑦age
⑧customer
⑨everywhere
⑩direction
【受験対策】数学-関数16

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
図のように,関数$y = ax^2$ グラフ上に,点$A(4,8)$がある.
また,点$B$,点$C$は$y$軸上の点で,
$\triangle ABC$は$AB = AC = 5$ の二等辺三角形である.
このとき,次の各問いに答えなさい.
①$a$の値を求めなさい.
②点$A$から$y$軸に垂線$AD$をひく.
この関数のグラフ上で,点$A$と原点$O$の間に点$P$をとり,
$\triangle ABC$の面積と$\triangle ADP$の面積が等しくなるようにする.
このとき,点$P$の$x$座標を求めなさい.
③点$C$を通り,$AB$に平行な直線と,この関数のグラフの交点のうち,
$x$座標が負である点を$E$とし,$EC$の延長と点$A$から
$x$軸にひいた垂線との交点を$F$とする.
このとき,②における点$P$において,
$\triangle OEF$の面積は$\triangle OPC$の面積の何倍か
求めなさい.
図は動画内参照
この動画を見る
図のように,関数$y = ax^2$ グラフ上に,点$A(4,8)$がある.
また,点$B$,点$C$は$y$軸上の点で,
$\triangle ABC$は$AB = AC = 5$ の二等辺三角形である.
このとき,次の各問いに答えなさい.
①$a$の値を求めなさい.
②点$A$から$y$軸に垂線$AD$をひく.
この関数のグラフ上で,点$A$と原点$O$の間に点$P$をとり,
$\triangle ABC$の面積と$\triangle ADP$の面積が等しくなるようにする.
このとき,点$P$の$x$座標を求めなさい.
③点$C$を通り,$AB$に平行な直線と,この関数のグラフの交点のうち,
$x$座標が負である点を$E$とし,$EC$の延長と点$A$から
$x$軸にひいた垂線との交点を$F$とする.
このとき,②における点$P$において,
$\triangle OEF$の面積は$\triangle OPC$の面積の何倍か
求めなさい.
図は動画内参照
【きっかけ英単語-26】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①box
②finger
③everyone
④person
⑤vegetable
⑥brave
⑦care
⑧crane
⑨pain
⑩character
この動画を見る
英単語を解説していきます.
①box
②finger
③everyone
④person
⑤vegetable
⑥brave
⑦care
⑧crane
⑨pain
⑩character
【受験対策】数学-証明3

単元:
#数学(中学生)#中1数学#中2数学#平行と合同#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右図のように,$\triangle ABC$の辺$BC$上に点$D$がある.
3点$A,B,D$を通る円と,辺$AC$との交点を$E$とするとき,
次の各問いに答えなさい.
①$\angle AEB=47°$のとき,$\angle ADC$の大きさを求めなさい.
②$AE=BD$のとき,$\triangle ACD\equiv \triangle BCE$を証明しなさい.
図は動画内参照
この動画を見る
右図のように,$\triangle ABC$の辺$BC$上に点$D$がある.
3点$A,B,D$を通る円と,辺$AC$との交点を$E$とするとき,
次の各問いに答えなさい.
①$\angle AEB=47°$のとき,$\angle ADC$の大きさを求めなさい.
②$AE=BD$のとき,$\triangle ACD\equiv \triangle BCE$を証明しなさい.
図は動画内参照
【きっかけ英単語-25】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①river
②breakfast
③child
④global
⑤hospital
⑥million
⑦such
⑧another
⑨its
⑩culture
この動画を見る
英単語を解説していきます.
①river
②breakfast
③child
④global
⑤hospital
⑥million
⑦such
⑧another
⑨its
⑩culture
【きっかけ英単語-24(月編)】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①1月
②2月
③3月
④4月
⑤5月
⑥6月
⑦7月
⑧8月
⑨9月
⑩10月
⑪11月
⑫12月
この動画を見る
英単語を解説していきます.
①1月
②2月
③3月
④4月
⑤5月
⑥6月
⑦7月
⑧8月
⑨9月
⑩10月
⑪11月
⑫12月
【きっかけ英単語-23(曜日編)】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①日曜日
②月曜日
③火曜日
④水曜日
⑤木曜日
⑥金曜日
⑦土曜日
この動画を見る
英単語を解説していきます.
①日曜日
②月曜日
③火曜日
④水曜日
⑤木曜日
⑥金曜日
⑦土曜日
【受験対策】数学-証明2

単元:
#数学(中学生)#中2数学#平行と合同
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図で,$\triangle ABC$は$AB=AC$の二等辺三角形,
$\triangle ACD$は$AC=AD$の二等辺三角形で,
頂点$D$から辺$CB$に平行な直線をひき,
辺$AB$との交点を$E$とする.
$AB=DE$のとき,次の各問いに答えなさい.
①$\triangle ABC$と$\triangle DEA$が合同であることを証明しなさい.
②$BD$と$AC$との交点を$F$とする.
$BC=BF$のとき,$\angle BAD$の大きさを求めなさい.
図は動画内参照
この動画を見る
右の図で,$\triangle ABC$は$AB=AC$の二等辺三角形,
$\triangle ACD$は$AC=AD$の二等辺三角形で,
頂点$D$から辺$CB$に平行な直線をひき,
辺$AB$との交点を$E$とする.
$AB=DE$のとき,次の各問いに答えなさい.
①$\triangle ABC$と$\triangle DEA$が合同であることを証明しなさい.
②$BD$と$AC$との交点を$F$とする.
$BC=BF$のとき,$\angle BAD$の大きさを求めなさい.
図は動画内参照
【きっかけ英単語-22】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①some
②any
③here
④family
⑤custom
⑥worth
⑦world
⑧beautiful
⑨same
⑩different
この動画を見る
英単語を解説していきます.
①some
②any
③here
④family
⑤custom
⑥worth
⑦world
⑧beautiful
⑨same
⑩different
【受験対策】数学-証明1

単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#平面図形#角度と面積#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図で,四角形$ABCD$は,$AD /\!/BC,AD\lt BC$の台形である.
辺$CD$の中点を$E$ とし,
辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と
$EA$の延長との交点を$G$とするとき,
次の各問いに答えなさい.
①$AE=FE$であることを証明しなさい.
②$\angle DAE=42°,\angle FEC=37$のとき,
$\angle CBG$の大きさを求めなさい.
図は動画内参照
この動画を見る
右の図で,四角形$ABCD$は,$AD /\!/BC,AD\lt BC$の台形である.
辺$CD$の中点を$E$ とし,
辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と
$EA$の延長との交点を$G$とするとき,
次の各問いに答えなさい.
①$AE=FE$であることを証明しなさい.
②$\angle DAE=42°,\angle FEC=37$のとき,
$\angle CBG$の大きさを求めなさい.
図は動画内参照
【きっかけ英単語-21】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①many
②much
③few
④little
⑤good
⑥library
⑦each
⑧kind
⑨example
⑩finally
この動画を見る
英単語を解説していきます.
①many
②much
③few
④little
⑤good
⑥library
⑦each
⑧kind
⑨example
⑩finally
【受験対策】数学-図形10

単元:
#算数(中学受験)#平面図形#図形の移動#平面図形その他#立体図形#立体図形その他
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図1は,半径が6cmで中心角が$90°$のおうぎ形と
直角三角形を組み合わせたものである.
$\boxed{1}$の部分と$\boxed{2}$の部分の面積が等しいとき,$x$の値を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
② 右の図2は,線分$AB$を直径とする円$O$を底面とし,
線分$AC$を母線とする円錐であり,
点$D$は線分$BC$の中点である.
$AB = 6cm,AC = 10cm$のとき,
2点$A,D$間の距離を求めなさい。
図は動画内参照
この動画を見る
①右の図1は,半径が6cmで中心角が$90°$のおうぎ形と
直角三角形を組み合わせたものである.
$\boxed{1}$の部分と$\boxed{2}$の部分の面積が等しいとき,$x$の値を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
② 右の図2は,線分$AB$を直径とする円$O$を底面とし,
線分$AC$を母線とする円錐であり,
点$D$は線分$BC$の中点である.
$AB = 6cm,AC = 10cm$のとき,
2点$A,D$間の距離を求めなさい。
図は動画内参照
【きっかけ英単語-20】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①bread
②thing
③slowly
④later
⑤fish
⑥hungry
⑦game
⑧traditional
⑨glad
⑩information
この動画を見る
英単語を解説していきます.
①bread
②thing
③slowly
④later
⑤fish
⑥hungry
⑦game
⑧traditional
⑨glad
⑩information
【きっかけ英単語-19】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①park
②only
③we
④famous
⑤popular
⑥interesting
⑦interested
⑧vacation
⑨job
⑩foreign
この動画を見る
英単語を解説していきます.
①park
②only
③we
④famous
⑤popular
⑥interesting
⑦interested
⑧vacation
⑨job
⑩foreign
【きっかけ英単語-18】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①product
②very
③sad
④yesterday
⑤village
⑥still
⑦quickly
⑧there
⑨almost
⑩pleasure
この動画を見る
英単語を解説していきます.
①product
②very
③sad
④yesterday
⑤village
⑥still
⑦quickly
⑧there
⑨almost
⑩pleasure
【きっかけ英単語-17】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①reason
②nature
③animal
④hot
⑤homework
⑥parents
⑦language
⑧enough
⑨detective
この動画を見る
英単語を解説していきます.
①reason
②nature
③animal
④hot
⑤homework
⑥parents
⑦language
⑧enough
⑨detective
【受験対策】数学-関数14

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図1で,曲線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフである.
四角形$ABCD$は正方形で,頂点$A$と頂点$D$は曲線上,
頂点$B$と頂点$C$は$x$軸上にある.
このとき,頂点$A$の座標を求めなさい.
②右の図2は,関数$y=ax^2(a\lt 0)$のグラフで,2点$A,B$は,
このグラフ上の点で,$x$座標はそれぞれ$-3,1$である.
2点$A,B$を通る直線の傾きが$3$のとき,$a$の値を求めなさい.
図は動画内参照
この動画を見る
①右の図1で,曲線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフである.
四角形$ABCD$は正方形で,頂点$A$と頂点$D$は曲線上,
頂点$B$と頂点$C$は$x$軸上にある.
このとき,頂点$A$の座標を求めなさい.
②右の図2は,関数$y=ax^2(a\lt 0)$のグラフで,2点$A,B$は,
このグラフ上の点で,$x$座標はそれぞれ$-3,1$である.
2点$A,B$を通る直線の傾きが$3$のとき,$a$の値を求めなさい.
図は動画内参照
【きっかけ英単語-16】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①always
②once
③often
④never
⑤again
⑥usually
⑦twice
⑧sometimes
⑨son
⑩daughter
この動画を見る
英単語を解説していきます.
①always
②once
③often
④never
⑤again
⑥usually
⑦twice
⑧sometimes
⑨son
⑩daughter
【受験対策】数学-関数13

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように,関数$y=x^2・・・(ア)$のグラフ上に2点,$A,B$がある.
軸上に点$C$をとり,四角形$ADBC$が平行四辺形となるように,点,$D$をとる.
点$A(-3.9)$,点$B(2.4)$のとき,次の各問いに答えなさい.
ただし,点$C$の$y$座標は,点$A$の$y$座標より大きいものとし,
座標の1目もりを1cmとする.
①関数②について,$x$の値が$-3$から$-1$まで増加するときの
変化の割合を求めなさい.
②関数③について,$x$の変域が$-1\leqq x\leqq 4$のとき,
$y$の変域を求めなさい.
③2点$A,B$を通る直線の式を求めなさい.
④平行四辺形$ADBC$の面積が$24cm^2$となるとき,
点$D$の座標を求めなさい.
図は動画内参照
この動画を見る
右の図のように,関数$y=x^2・・・(ア)$のグラフ上に2点,$A,B$がある.
軸上に点$C$をとり,四角形$ADBC$が平行四辺形となるように,点,$D$をとる.
点$A(-3.9)$,点$B(2.4)$のとき,次の各問いに答えなさい.
ただし,点$C$の$y$座標は,点$A$の$y$座標より大きいものとし,
座標の1目もりを1cmとする.
①関数②について,$x$の値が$-3$から$-1$まで増加するときの
変化の割合を求めなさい.
②関数③について,$x$の変域が$-1\leqq x\leqq 4$のとき,
$y$の変域を求めなさい.
③2点$A,B$を通る直線の式を求めなさい.
④平行四辺形$ADBC$の面積が$24cm^2$となるとき,
点$D$の座標を求めなさい.
図は動画内参照
【きっかけ英単語-15】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①where
②what
③which
④who
⑤whose
⑥when
⑦why
⑧how
⑨how many~
⑩how much
この動画を見る
英単語を解説していきます.
①where
②what
③which
④who
⑤whose
⑥when
⑦why
⑧how
⑨how many~
⑩how much
【きっかけ英単語-14】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①so
②and
③but
④if
⑤because
⑥untill
⑦till
⑧or
⑨while
⑩although
この動画を見る
英単語を解説していきます.
①so
②and
③but
④if
⑤because
⑥untill
⑦till
⑧or
⑨while
⑩although
【きっかけ英単語-13】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英単語を解説していきます.
①can
②Can you~?
③Can I~?
④will
⑤Will you~?
⑥must
⑦should
⑧may
⑨May I~?
⑩Shall I~?
この動画を見る
英単語を解説していきます.
①can
②Can you~?
③Can I~?
④will
⑤Will you~?
⑥must
⑦should
⑧may
⑨May I~?
⑩Shall I~?
【受験対策】数学-図形9

単元:
#数学(中学生)#中1数学#空間図形#平面図形#角度と面積#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図1で,$\ell /\!/ m$のとき,
$\angle x +\angle y$の大きさを求めなさい.
② 右の図2で,半径3cm,中心角$90°$のおうぎ形がある.
これを,辺$AC$を軸として1回転させてできる立体の表面積を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
③右の図3は,直角三角形と2つの半円を組み合わせたものである.
3つの$\boxminus$部分の面積の合計を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
図は動画内参照
この動画を見る
①右の図1で,$\ell /\!/ m$のとき,
$\angle x +\angle y$の大きさを求めなさい.
② 右の図2で,半径3cm,中心角$90°$のおうぎ形がある.
これを,辺$AC$を軸として1回転させてできる立体の表面積を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
③右の図3は,直角三角形と2つの半円を組み合わせたものである.
3つの$\boxminus$部分の面積の合計を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
図は動画内参照
【中2 P.30】1編の力だめし
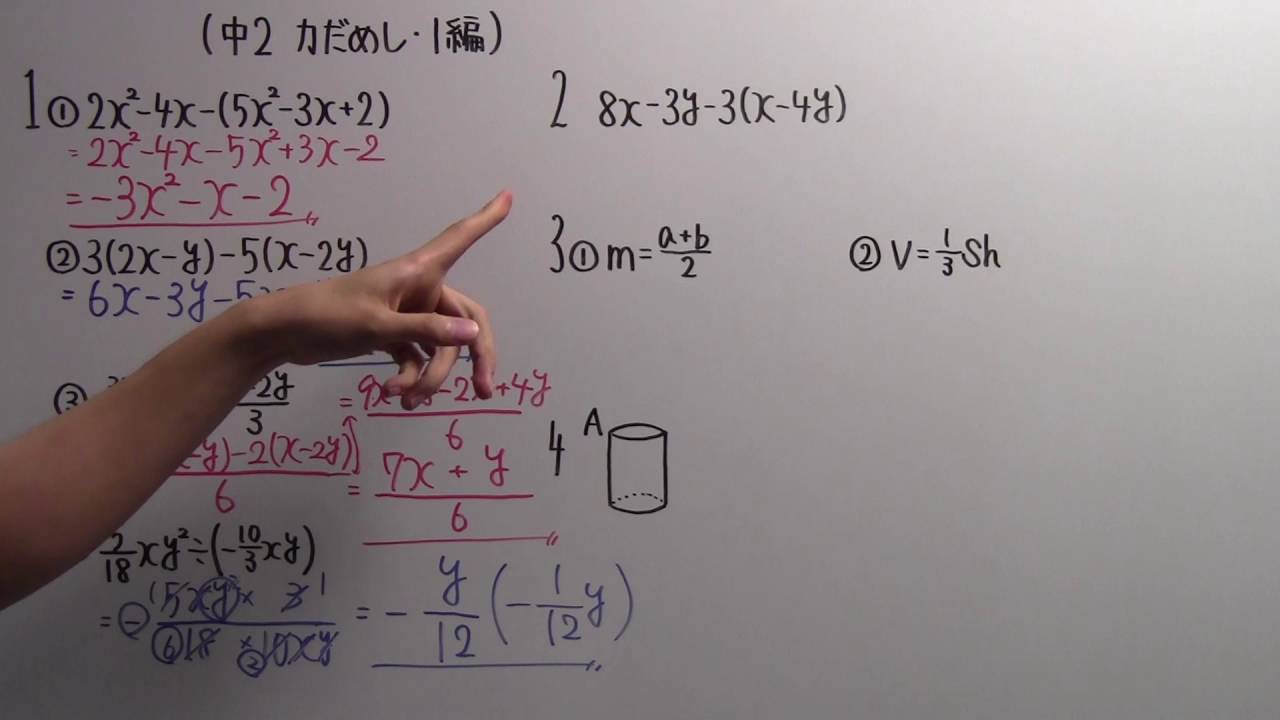
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の計算をしよう.
1①$2x^2-4x-(5x^2-3x+2)$
②$3(2x-y)-5(x-2y)$
③$\dfrac{3x-y}{2}-\dfrac{x-2y}{3}$
④$\dfrac{5}{18}xy^2\div \left(-\dfrac{10}{3}xy\right)$
2.$8x-3y-3(x-4y)$
3.①$m=\dfrac{a+b}{2}$
②$V=\dfrac{1}{3}sh$
図は動画内参照
この動画を見る
次の計算をしよう.
1①$2x^2-4x-(5x^2-3x+2)$
②$3(2x-y)-5(x-2y)$
③$\dfrac{3x-y}{2}-\dfrac{x-2y}{3}$
④$\dfrac{5}{18}xy^2\div \left(-\dfrac{10}{3}xy\right)$
2.$8x-3y-3(x-4y)$
3.①$m=\dfrac{a+b}{2}$
②$V=\dfrac{1}{3}sh$
図は動画内参照
【中1 P.164】6編の力だめし
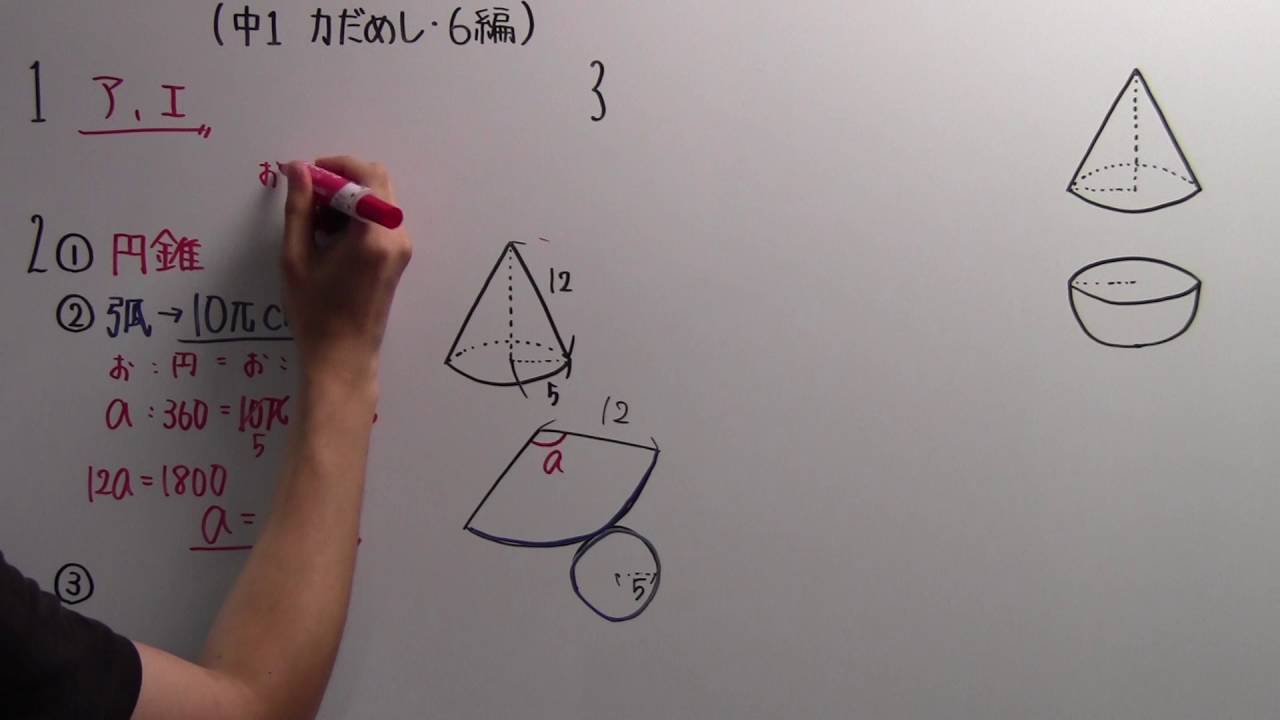
【中1 P.94】方程式の計算特訓①

単元:
#数学(中学生)#中1数学#方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1.次の計算をしよう.
$\boxed{1} \quad 5x+4=3x+12$
$\boxed{2} \quad 9-x=5$
$\boxed{3} \quad 3(x-4)=5x+2$
$\boxed{4} \quad \dfrac{3}{2}x-1=4-x$
$\boxed{5} \quad \dfrac{x+4}{3}+1=\dfrac{3x-7}{2}$
$\boxed{6} \quad 0.4x+0.5=2.6-0.3x$
$\boxed{7} \quad 1.5x-3=\dfrac{6}{5}x-0.3$
$\boxed{8} \quad \dfrac{1}{2}x+\dfrac{3}{4}=\dfrac{3}{8}x-\dfrac{1}{2}$
この動画を見る
1.次の計算をしよう.
$\boxed{1} \quad 5x+4=3x+12$
$\boxed{2} \quad 9-x=5$
$\boxed{3} \quad 3(x-4)=5x+2$
$\boxed{4} \quad \dfrac{3}{2}x-1=4-x$
$\boxed{5} \quad \dfrac{x+4}{3}+1=\dfrac{3x-7}{2}$
$\boxed{6} \quad 0.4x+0.5=2.6-0.3x$
$\boxed{7} \quad 1.5x-3=\dfrac{6}{5}x-0.3$
$\boxed{8} \quad \dfrac{1}{2}x+\dfrac{3}{4}=\dfrac{3}{8}x-\dfrac{1}{2}$
【中2 P.104】4編の力だめし

【中1 P.128】4編の力だめし
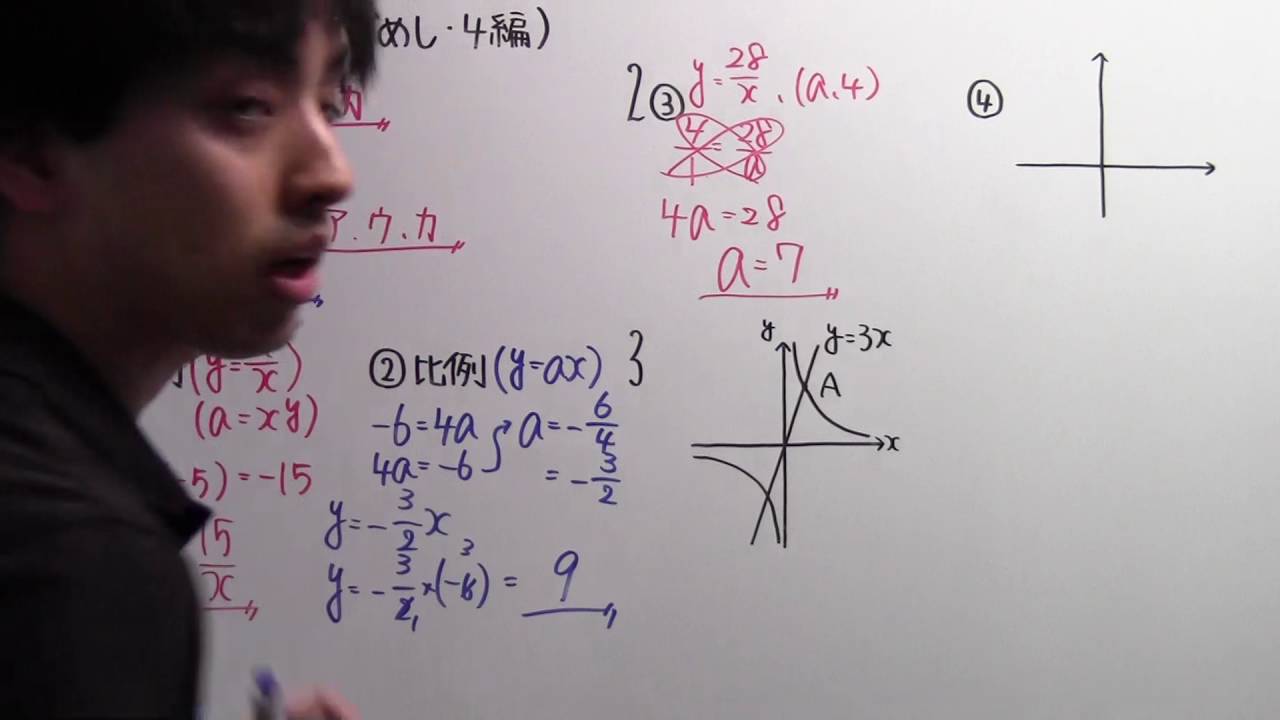
【中2 P.124】5編の力だめし
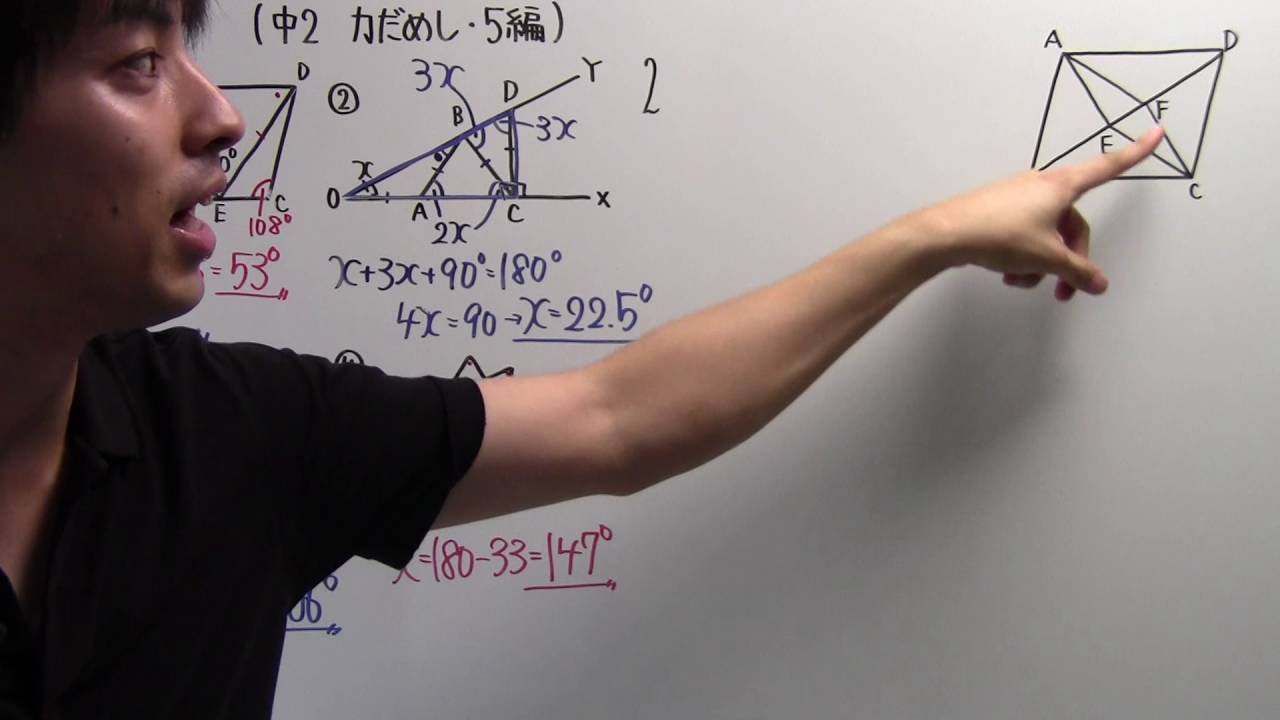
【中1 P.95】方程式の計算特訓②

単元:
#数学(中学生)#中1数学#方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
2.次の計算をしよう.
$\boxed{1} \quad x:5=8:2$
$\boxed{2} \quad 3:x=7:3$
$\boxed{3} \quad (x-5):3=16:12$
$\boxed{4} \quad 2:x=3:(x+5)$
$\boxed{5} \quad (x+7):6=x:\dfrac{5}{2}$
$\boxed{6} \quad (x-2):3=(x+1):5$
この動画を見る
2.次の計算をしよう.
$\boxed{1} \quad x:5=8:2$
$\boxed{2} \quad 3:x=7:3$
$\boxed{3} \quad (x-5):3=16:12$
$\boxed{4} \quad 2:x=3:(x+5)$
$\boxed{5} \quad (x+7):6=x:\dfrac{5}{2}$
$\boxed{6} \quad (x-2):3=(x+1):5$


