 とある男が授業をしてみた
とある男が授業をしてみた
 とある男が授業をしてみた
とある男が授業をしてみた
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
港を見てみよう!【小学校 社会】

【高校受験対策/数学】死守81(問題作りました)

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#1次関数#平行と合同#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守81
①$81÷(-3)-(-11)$を計算しなさい。
②次の式を因数分解しなさい。
$(x-2)^2-18(x-2)+81$
③次の連立方程式を解きなさい。
$3x+11y=13$
$2x-3y=19$
④$311x-8y=1$を$y$について解きなさい。
⑤絶対値が$81$である数をすべて書きなさい。
⑥右の図において2直線$l,m$は平行である。
このとき、$\angle x$の大きさを求めなさい。
⑦3点$(-3,-11)$、$(2,9)$、$(k,81)$が一直線上にあるとき、 $k$の値を求めなさい。
⑧定価$8100$円のパーカーが$a$割引で売っていた。
それを買おうとレジに持っていくと、キャンペーンだったようで、そこからさらに$500$円引きしてくれた。
このとき、パーカーを買ったときの代金を$a$を使った式で表しなさい。
ただし消費税については考えないものとする。
この動画を見る
高校受験対策・死守81
①$81÷(-3)-(-11)$を計算しなさい。
②次の式を因数分解しなさい。
$(x-2)^2-18(x-2)+81$
③次の連立方程式を解きなさい。
$3x+11y=13$
$2x-3y=19$
④$311x-8y=1$を$y$について解きなさい。
⑤絶対値が$81$である数をすべて書きなさい。
⑥右の図において2直線$l,m$は平行である。
このとき、$\angle x$の大きさを求めなさい。
⑦3点$(-3,-11)$、$(2,9)$、$(k,81)$が一直線上にあるとき、 $k$の値を求めなさい。
⑧定価$8100$円のパーカーが$a$割引で売っていた。
それを買おうとレジに持っていくと、キャンペーンだったようで、そこからさらに$500$円引きしてくれた。
このとき、パーカーを買ったときの代金を$a$を使った式で表しなさい。
ただし消費税については考えないものとする。
【高校受験対策/数学】死守-80

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#2次方程式#空間図形#1次関数#確率#2次関数#文字と式#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守80
①$-3+(-4)×5$を計算しなさい。
②$4xy÷8x×6y$を計算しなさい。
③$\frac{4x-y}{2}-(2x-3y)$を計算しなさい。
④連立方程式を解きなさい。
$5x-4y=9$
$2x-3y=5$
③下の図で、$\angle x$の大きさを求めなさい。
④地球の直径は約$12700km$です。
有効数字が$1,2,7$であるとして、この距離を整数部分が1けたの数と、10の何乗かの積の形で表すと右のようになります。
アとイにあてはまる数を書きなさい。
⑦半径が$2cm$の球の体積と表面積を求めなさい。ただし円周率は$\pi$とする。
⑧赤玉3個と白玉2個が入っている袋があります。
この袋から玉を1個取り出して色を確認して、それを袋に戻してから、もう一度玉を1個取り出して色を確認します。
このとき、2回とも同じ色の玉が出る確率を求めなさい。
ただし、袋の中は見えないものとし、どの玉が出ることも同様に確からしいものとする。
⑨関数$y=ax^2$について、$x$の変域が$-2 \leqq x \leqq 3$のとき、$y$の変域は$-3b \leqq y \leqq 0$となりました。
このとき$a$の値を求めなさい。
この動画を見る
高校受験対策・死守80
①$-3+(-4)×5$を計算しなさい。
②$4xy÷8x×6y$を計算しなさい。
③$\frac{4x-y}{2}-(2x-3y)$を計算しなさい。
④連立方程式を解きなさい。
$5x-4y=9$
$2x-3y=5$
③下の図で、$\angle x$の大きさを求めなさい。
④地球の直径は約$12700km$です。
有効数字が$1,2,7$であるとして、この距離を整数部分が1けたの数と、10の何乗かの積の形で表すと右のようになります。
アとイにあてはまる数を書きなさい。
⑦半径が$2cm$の球の体積と表面積を求めなさい。ただし円周率は$\pi$とする。
⑧赤玉3個と白玉2個が入っている袋があります。
この袋から玉を1個取り出して色を確認して、それを袋に戻してから、もう一度玉を1個取り出して色を確認します。
このとき、2回とも同じ色の玉が出る確率を求めなさい。
ただし、袋の中は見えないものとし、どの玉が出ることも同様に確からしいものとする。
⑨関数$y=ax^2$について、$x$の変域が$-2 \leqq x \leqq 3$のとき、$y$の変域は$-3b \leqq y \leqq 0$となりました。
このとき$a$の値を求めなさい。
【高校受験対策/数学】死守-79

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#文字と式#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守79
①$-3-(-7)$を計算しなさい。
②$8a^3b^5÷4a^2b^3$を計算しなさい。
③$x^2-8x+16$を因数分解しなさい。
④$a=\frac{2b-c}{5}$を$c$について解きなさい。
⑤二次方程式$x^2+5x+2=0$を解きなさい。
⑥$a=2$、$b=-3$のとき、$a+b^2$の値を求めなさい。
⑦次の文の( )に当てはまる条件として最も適切なものを、ア~エから1つ選んで記号で答えなさい。
平行四辺形$ABCD$に、( )の条件が加わると、平行四辺形$ABCD$は長方形になる。
ア $AB=BC$
イ $AC\perp BD$
ウ $AC=BD$
エ $\angle ABD=\angle CBD$
⑧$A$地点から$B$地点まで、初めは毎分$60m$で$am$歩き、途中から毎分$100m$で$bm$走ったところ、$20$分以内で$B$地点に到着した。この数量の関係を不等式で表しなさい。
⑨次のア~エのうちから、内容が正しいものを1つ選んで記号で答えなさい。
ア $9$の平方根は$3$と$-3$である。
イ $\sqrt{16}$を根号を使わずに表すと$\pm 4$である。
ウ $\sqrt{5}+\sqrt{7}$と$\sqrt{5+7}$は同じ値である。
エ $(\sqrt{2}+\sqrt{6})^2$と$(\sqrt{2})^2+(\sqrt{6})^2$は同じ値である。
この動画を見る
高校受験対策・死守79
①$-3-(-7)$を計算しなさい。
②$8a^3b^5÷4a^2b^3$を計算しなさい。
③$x^2-8x+16$を因数分解しなさい。
④$a=\frac{2b-c}{5}$を$c$について解きなさい。
⑤二次方程式$x^2+5x+2=0$を解きなさい。
⑥$a=2$、$b=-3$のとき、$a+b^2$の値を求めなさい。
⑦次の文の( )に当てはまる条件として最も適切なものを、ア~エから1つ選んで記号で答えなさい。
平行四辺形$ABCD$に、( )の条件が加わると、平行四辺形$ABCD$は長方形になる。
ア $AB=BC$
イ $AC\perp BD$
ウ $AC=BD$
エ $\angle ABD=\angle CBD$
⑧$A$地点から$B$地点まで、初めは毎分$60m$で$am$歩き、途中から毎分$100m$で$bm$走ったところ、$20$分以内で$B$地点に到着した。この数量の関係を不等式で表しなさい。
⑨次のア~エのうちから、内容が正しいものを1つ選んで記号で答えなさい。
ア $9$の平方根は$3$と$-3$である。
イ $\sqrt{16}$を根号を使わずに表すと$\pm 4$である。
ウ $\sqrt{5}+\sqrt{7}$と$\sqrt{5+7}$は同じ値である。
エ $(\sqrt{2}+\sqrt{6})^2$と$(\sqrt{2})^2+(\sqrt{6})^2$は同じ値である。
【高校受験対策/数学】関数56

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数56
Q.
図のように、円の中心$O$と点$P$が直線$l$上にあり、円の$O$半径は10$cm$、$OP$間の距離は20$cm$である。
点$O$が固定されたまま、点$P$は毎秒3$cm$の速さで直線$l$上を図の矢印の向きに進み、出発してから10秒後に停止する。
点$P$が出発してから$x$秒後の$OP$間の距離を$y cm$として次の問いに答えなさい。
①点$P$が出発してから点$O$と重なるまでの間について、$y$を$x$の式で表しなさい。
②点$P$が点$O$と重なってから停止するまでの間について、$y$を$x$の式で表しなさい。
③点$P$が出発してから停止するまでの間において、点$P$が円$O$の周上または内部にある時間は何秒間か求めなさい。
④点$P$が出来するのと同時に、毎秒1$cm$の一定の割合で円の半径が小さくなり始め、点$P$が停止するまでの間、円$O$は中心が固定されたまま徐々に小さくなっていくものとする。
点$P$が出発してから停止するまでの間において、点$P$が円$O$の周上または内部にある時間は何秒間か求めなさい。
この動画を見る
高校受験対策・関数56
Q.
図のように、円の中心$O$と点$P$が直線$l$上にあり、円の$O$半径は10$cm$、$OP$間の距離は20$cm$である。
点$O$が固定されたまま、点$P$は毎秒3$cm$の速さで直線$l$上を図の矢印の向きに進み、出発してから10秒後に停止する。
点$P$が出発してから$x$秒後の$OP$間の距離を$y cm$として次の問いに答えなさい。
①点$P$が出発してから点$O$と重なるまでの間について、$y$を$x$の式で表しなさい。
②点$P$が点$O$と重なってから停止するまでの間について、$y$を$x$の式で表しなさい。
③点$P$が出発してから停止するまでの間において、点$P$が円$O$の周上または内部にある時間は何秒間か求めなさい。
④点$P$が出来するのと同時に、毎秒1$cm$の一定の割合で円の半径が小さくなり始め、点$P$が停止するまでの間、円$O$は中心が固定されたまま徐々に小さくなっていくものとする。
点$P$が出発してから停止するまでの間において、点$P$が円$O$の周上または内部にある時間は何秒間か求めなさい。
【高校受験対策/数学】死守-78

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#1次関数#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守78
①下の図のように、長方形$ABCD$の中に 1辺の長さが$\sqrt{5}cm$と$\sqrt{10}cm$の正方形がある。
このとき、斜線部分の長方形の間の長さを求めなさい。
②葉一くんは、下の図の平行四辺形$ABCD$の面積を求めるために、辺$BC$を底辺とみて、高さを測ろうと考えた。
点を$P$下の図のようにとるとき、線分$PH$が高さとなるような点$H$を作図によって求めなさい。
③1000円で、1個$a$円のクリームパン5個と1個$b$円のジャムパン3個を買うことができる。
ただし消費税は考えないものとする。
この数量の関係を表した不等式としてもっとも適切なものを、次の ア~エの中から一つ選んで、その記号を書きなさい。
ア $1000-(5a+3b) \lt 0$
イ $5a+3b \lt 1000$
ウ $1000-(5a+3b) \geqq 0$
エ $(5a+3b) \geqq 1000$
④ 右の図で、点$A$は関数$y=\frac{2}{x }$と関数$y=ax^2$のグラフの交点である。
点$B$は点$A$を$y$軸を対称の軸として対称移動させたものであり、$x$座標は$-1$である。
このことから、$a$の値はアであり、関数$y=ax^2$について、 $x$の値が1から3まで増加するときの変化の割合はイであることがわ かる。
このとき上のア・イに当てはまる数をそれぞれ書きなさい。
この動画を見る
高校受験対策・死守78
①下の図のように、長方形$ABCD$の中に 1辺の長さが$\sqrt{5}cm$と$\sqrt{10}cm$の正方形がある。
このとき、斜線部分の長方形の間の長さを求めなさい。
②葉一くんは、下の図の平行四辺形$ABCD$の面積を求めるために、辺$BC$を底辺とみて、高さを測ろうと考えた。
点を$P$下の図のようにとるとき、線分$PH$が高さとなるような点$H$を作図によって求めなさい。
③1000円で、1個$a$円のクリームパン5個と1個$b$円のジャムパン3個を買うことができる。
ただし消費税は考えないものとする。
この数量の関係を表した不等式としてもっとも適切なものを、次の ア~エの中から一つ選んで、その記号を書きなさい。
ア $1000-(5a+3b) \lt 0$
イ $5a+3b \lt 1000$
ウ $1000-(5a+3b) \geqq 0$
エ $(5a+3b) \geqq 1000$
④ 右の図で、点$A$は関数$y=\frac{2}{x }$と関数$y=ax^2$のグラフの交点である。
点$B$は点$A$を$y$軸を対称の軸として対称移動させたものであり、$x$座標は$-1$である。
このことから、$a$の値はアであり、関数$y=ax^2$について、 $x$の値が1から3まで増加するときの変化の割合はイであることがわ かる。
このとき上のア・イに当てはまる数をそれぞれ書きなさい。
【高校受験対策/数学】???

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
【高校受験対策/数学】???
ある中学校の全校の生徒数は、男女合わせて155人です。
この中学校の男子生徒の80%と女子生徒の60%が運動部に所属しており、
運動部に所属している男子の人数は、 運動部に所属している女子の人数より19人多い。
このとき運動部に所属している男子の人数と運動部に所属している女子の人数を、それぞれ求めなさい。
この動画を見る
【高校受験対策/数学】???
ある中学校の全校の生徒数は、男女合わせて155人です。
この中学校の男子生徒の80%と女子生徒の60%が運動部に所属しており、
運動部に所属している男子の人数は、 運動部に所属している女子の人数より19人多い。
このとき運動部に所属している男子の人数と運動部に所属している女子の人数を、それぞれ求めなさい。
【高校受験対策/数学】死守77

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守77
①$-3+(-2)$を計算しなさい。
➁$8-4÷(-2)^2$を計算しなさい。
③$5×(-5a)$を計算しなさい。
④$\frac{1}{2}x^2y÷\frac{1}{4}xy$を計算しなさい。
⑤$\sqrt{48}-\sqrt{3}$を計算しなさい。
⑥$(2a-b)^2$を展開しなさい。
⑦$x^2-x-42$を因数分解しなさい。
⑧半径が$6cm$で中心角が$45°$のおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨解が$-5,1$の2つの数となる、$x$についての2次方程式を1つ作りなさい。
⑩次のア~エのうち、数の集合と四則との関係について述べた文として正しいものをすべて選び、記号で答えなさい。
ア 自然数と自然数の加法の結果は、いつでも自然数となる。
イ 自然数と自然数の減法の結果は、いつでも整数となる。
ウ 自然数と自然数の乗法の結果は、いつでも自然数となる。
エ 自然数と自然数の除法の結果は、いつでも整数となる。
この動画を見る
高校受験対策・死守77
①$-3+(-2)$を計算しなさい。
➁$8-4÷(-2)^2$を計算しなさい。
③$5×(-5a)$を計算しなさい。
④$\frac{1}{2}x^2y÷\frac{1}{4}xy$を計算しなさい。
⑤$\sqrt{48}-\sqrt{3}$を計算しなさい。
⑥$(2a-b)^2$を展開しなさい。
⑦$x^2-x-42$を因数分解しなさい。
⑧半径が$6cm$で中心角が$45°$のおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨解が$-5,1$の2つの数となる、$x$についての2次方程式を1つ作りなさい。
⑩次のア~エのうち、数の集合と四則との関係について述べた文として正しいものをすべて選び、記号で答えなさい。
ア 自然数と自然数の加法の結果は、いつでも自然数となる。
イ 自然数と自然数の減法の結果は、いつでも整数となる。
ウ 自然数と自然数の乗法の結果は、いつでも自然数となる。
エ 自然数と自然数の除法の結果は、いつでも整数となる。
【高校受験対策/数学】図形40

単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形40
図1のように、点$O$を中心とし線分$AB$を直径とする 半径$3cm$の半円がある。
$\stackrel{\huge\frown}{AB}$上に2点$P,Q$があり、$A$に近い方を$P$、$B$に近い方を$Q$とする。
また、線分$BP$と線分$OQ$の交点を$R$とし、線分$AQ$と線分$BP$の交点を$S$とする。
このとき、次の問いに答えなさい。
①$\triangle RQC \backsim \triangle RPQ$を証明しなさい。
②図2のように、$\angle QOC=90°$、$OS /\!/ BQ$となるとき、線分$BR$の長さを求めなさい。
この動画を見る
高校受験対策・図形40
図1のように、点$O$を中心とし線分$AB$を直径とする 半径$3cm$の半円がある。
$\stackrel{\huge\frown}{AB}$上に2点$P,Q$があり、$A$に近い方を$P$、$B$に近い方を$Q$とする。
また、線分$BP$と線分$OQ$の交点を$R$とし、線分$AQ$と線分$BP$の交点を$S$とする。
このとき、次の問いに答えなさい。
①$\triangle RQC \backsim \triangle RPQ$を証明しなさい。
②図2のように、$\angle QOC=90°$、$OS /\!/ BQ$となるとき、線分$BR$の長さを求めなさい。
【高校受験対策/数学】死守76

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#比例・反比例#空間図形#確率#文字と式#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守76
①$2-(-5)$を計算しなさい。
②$4x-2x×\frac{1}{2}$を計算しなさい。
③$-6a^3b^2÷(-4ab)$を計算しなさい。
④$x=-2$、$y=3$のとき$(2x-y-6)+3(x+y+2)$の値を求めなさい。
③下の図の三角柱$ABC-DEF$において、 辺$AB$とねじれの位置にある辺をすべて答えなさい。
⑥$n$を自然数とする。$\sqrt{24n}$が自然数となるような$n$のうち、最も小さい数を求めなさい。
⑦2つの容器A、Bに牛乳が入っており、容器Bに入っている牛乳の量は、容器Aに入っている牛乳の量の2倍である。
容器Aに$140ml$の牛乳を加えたところ、 容器Aと容器Bの牛乳の量の比が$5:3$となった。
はじめに容器Aに入って いた牛乳の量は何$ml$であったか、求めなさい。
⑧あるクラスの女子生徒20人が体カテストで反復横とびを行い、
その記録を整理したところ、20人の記録の中央値は50回であった。
この20人の記録について、次のア~エのうち、必ず正しいといえるものを1つ選びなさい。
ア 20人の記録の合計は1000回である。
イ 20人のうち、記録が50回であった生徒が最も多い。
ウ 20人のうち、記録が60回以上であった生徒は1人もいない。
エ 20人のうち、記録が50回以上であった生徒が少なくとも10人いる。
この動画を見る
高校受験対策・死守76
①$2-(-5)$を計算しなさい。
②$4x-2x×\frac{1}{2}$を計算しなさい。
③$-6a^3b^2÷(-4ab)$を計算しなさい。
④$x=-2$、$y=3$のとき$(2x-y-6)+3(x+y+2)$の値を求めなさい。
③下の図の三角柱$ABC-DEF$において、 辺$AB$とねじれの位置にある辺をすべて答えなさい。
⑥$n$を自然数とする。$\sqrt{24n}$が自然数となるような$n$のうち、最も小さい数を求めなさい。
⑦2つの容器A、Bに牛乳が入っており、容器Bに入っている牛乳の量は、容器Aに入っている牛乳の量の2倍である。
容器Aに$140ml$の牛乳を加えたところ、 容器Aと容器Bの牛乳の量の比が$5:3$となった。
はじめに容器Aに入って いた牛乳の量は何$ml$であったか、求めなさい。
⑧あるクラスの女子生徒20人が体カテストで反復横とびを行い、
その記録を整理したところ、20人の記録の中央値は50回であった。
この20人の記録について、次のア~エのうち、必ず正しいといえるものを1つ選びなさい。
ア 20人の記録の合計は1000回である。
イ 20人のうち、記録が50回であった生徒が最も多い。
ウ 20人のうち、記録が60回以上であった生徒は1人もいない。
エ 20人のうち、記録が50回以上であった生徒が少なくとも10人いる。
船が無くなったらどうなるの?【小学校 社会】

単元:
#社会(中学受験)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
社会(船がなくなったらどうなるの?
ポイント
日本の貿易量の①%が海上輸送なんだ!
日本は資源が多い国ではないから、
衣・食・住や産業に必要な原料を外国からの②でまかなっている。
その方法は③を利用した航空輸送と④を利用した海上輸送があるんだ。
もし日本から船がパッと消えてしまったら⑤も無くなってしまうし、
⑥やガスも使えなくなってしまうよ。
この動画を見る
社会(船がなくなったらどうなるの?
ポイント
日本の貿易量の①%が海上輸送なんだ!
日本は資源が多い国ではないから、
衣・食・住や産業に必要な原料を外国からの②でまかなっている。
その方法は③を利用した航空輸送と④を利用した海上輸送があるんだ。
もし日本から船がパッと消えてしまったら⑤も無くなってしまうし、
⑥やガスも使えなくなってしまうよ。
【高校受験対策/数学】関数55

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数55
Q.
図1のように、関数$y=-\frac{1}{4}x^2$・・・①のグラフ上に点$A(4,-4)$があり、$x$軸上に点$P$がある。
また、点$B(-2,-4)$がある。
問1
関数$y=-\frac{1}{4}x^2$について、$x$の変域が$-6 \leqq x \leqq 1$のとき、$y$の変域を求めなさい。
問2
$\triangle PAB$が二等辺三角形となる$P$はいくつあるか、求めなさい。
問3
図2のように、関数$y=ax^2(a \gt0)$・・・②のグラフ上に、 $x$座標が$-3$である点$D$がある。
$P$の$x$座標が$4$のとき、四角形$PABD$の面積が$50$となるような$a$の値を求めなさい。
この動画を見る
高校受験対策・関数55
Q.
図1のように、関数$y=-\frac{1}{4}x^2$・・・①のグラフ上に点$A(4,-4)$があり、$x$軸上に点$P$がある。
また、点$B(-2,-4)$がある。
問1
関数$y=-\frac{1}{4}x^2$について、$x$の変域が$-6 \leqq x \leqq 1$のとき、$y$の変域を求めなさい。
問2
$\triangle PAB$が二等辺三角形となる$P$はいくつあるか、求めなさい。
問3
図2のように、関数$y=ax^2(a \gt0)$・・・②のグラフ上に、 $x$座標が$-3$である点$D$がある。
$P$の$x$座標が$4$のとき、四角形$PABD$の面積が$50$となるような$a$の値を求めなさい。
【高校受験対策/数学】死守75

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#平行と合同#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
この動画を見る
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
【高校受験対策/数学】死守74

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#空間図形#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守74
①$6-17$を計算しなさい。
②$6÷(-\frac{2}{3})$を計算しなさい。
③$2x+3y-(\frac{x+5y}{2})$を計算しなさい。
④$(\sqrt{3}+1)(\sqrt{3}-3)$を計算しなさい。
⑤ 下の図のような、平行四辺形$ABCD$がある。このとき$\angle x$の大きさを求めなさい。
⑥右の図のように、1辺の長さが$4cm$の立方体にちょうど入る大きさの球がある。
この球の体積を求めなさい。
⑦$am$のリボンから$bm$切り取ると、残りのリボンの長さは$2m$より短い。
この数量の関係を不等式で表しなさい。
⑧ある小学校で、工場の見学に行くために電車を利用することになった。
通常は児童15人と先生2人が支払う運賃の合計が9100円になる。
しかし、児童が10人以上いるとき児童の運賃のみが4割引きになる。
このため、児童15人と先生2人の運賃との合計は6100円になった。
このとき、割引きされた後の児童1人分の運賃を求めなさい。
この動画を見る
高校受験対策・死守74
①$6-17$を計算しなさい。
②$6÷(-\frac{2}{3})$を計算しなさい。
③$2x+3y-(\frac{x+5y}{2})$を計算しなさい。
④$(\sqrt{3}+1)(\sqrt{3}-3)$を計算しなさい。
⑤ 下の図のような、平行四辺形$ABCD$がある。このとき$\angle x$の大きさを求めなさい。
⑥右の図のように、1辺の長さが$4cm$の立方体にちょうど入る大きさの球がある。
この球の体積を求めなさい。
⑦$am$のリボンから$bm$切り取ると、残りのリボンの長さは$2m$より短い。
この数量の関係を不等式で表しなさい。
⑧ある小学校で、工場の見学に行くために電車を利用することになった。
通常は児童15人と先生2人が支払う運賃の合計が9100円になる。
しかし、児童が10人以上いるとき児童の運賃のみが4割引きになる。
このため、児童15人と先生2人の運賃との合計は6100円になった。
このとき、割引きされた後の児童1人分の運賃を求めなさい。
【高校受験対策/数学】死守73

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#確率#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守73
①$-9+(-8)$を計算しなさい。
②$\frac{3}{4}÷-(\frac{5}{6})$を計算しなさい。
③$2(a+46)-(-3a+7b) を計算しなさい。
④$\sqrt{12}×\sqrt{2}÷\sqrt{6}$を計算しなさい。
⑤二次方程式$3x^2-x-1=0$を解きなさい。
⑥連立方程式を解きなさい。
$2x+3y=20$
$4y=x+1$
⑦2つのさいころを同時に投げるとき、出る目の和が8に ならない確率を求めなさい。
ただし、どの目が出ることも同様に確からしいとする。
⑧右の図のように、線分$OA$、$OB$がある。
$\angle AOB$の二等分線上にあり、2点$O,B$から等しい距離にある点$P$を、コンパスと定規を使って作図しなさい。
この動画を見る
高校受験対策・死守73
①$-9+(-8)$を計算しなさい。
②$\frac{3}{4}÷-(\frac{5}{6})$を計算しなさい。
③$2(a+46)-(-3a+7b) を計算しなさい。
④$\sqrt{12}×\sqrt{2}÷\sqrt{6}$を計算しなさい。
⑤二次方程式$3x^2-x-1=0$を解きなさい。
⑥連立方程式を解きなさい。
$2x+3y=20$
$4y=x+1$
⑦2つのさいころを同時に投げるとき、出る目の和が8に ならない確率を求めなさい。
ただし、どの目が出ることも同様に確からしいとする。
⑧右の図のように、線分$OA$、$OB$がある。
$\angle AOB$の二等分線上にあり、2点$O,B$から等しい距離にある点$P$を、コンパスと定規を使って作図しなさい。
【高校受験対策/数学】死守72

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#空間図形#平行と合同#確率#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守72
①$2-6$を計算しなさい。
➁$-3×(-2^2)$を計算しなさい。
③$\frac{2a+b}{ 3 }+\frac{a-b}{ 2 }$を計算しなさい。
④$xy^2×x^2÷xy$を計算しなさい。
⑤$\frac{6}{\sqrt{3}}+\sqrt{15}×\sqrt{5}$を計算しなさい。
⑥2次方程式$x^2+7x-18=0$ を解きなさい。
⑦$a=\sqrt{5}+3$のとき、$a^2-6a+9$の値を求めなさい。
⑧500円、100円、50円の硬貨が1枚ずつある。
この3枚を同時に1回投げるとき、表が出た硬貨の合計金額が500円以下になる確率を求めなさい。
ただし3枚の硬貨のそれぞれについて、表と裏の出方は同様に確からしいとする。
⑨右の図は底面の半径が$3cm$、側面になるおうぎ形の半径が$5cm$の円錐の展開図である。
これを組み立ててできる円錐の体積を求めなさい。
この動画を見る
高校受験対策・死守72
①$2-6$を計算しなさい。
➁$-3×(-2^2)$を計算しなさい。
③$\frac{2a+b}{ 3 }+\frac{a-b}{ 2 }$を計算しなさい。
④$xy^2×x^2÷xy$を計算しなさい。
⑤$\frac{6}{\sqrt{3}}+\sqrt{15}×\sqrt{5}$を計算しなさい。
⑥2次方程式$x^2+7x-18=0$ を解きなさい。
⑦$a=\sqrt{5}+3$のとき、$a^2-6a+9$の値を求めなさい。
⑧500円、100円、50円の硬貨が1枚ずつある。
この3枚を同時に1回投げるとき、表が出た硬貨の合計金額が500円以下になる確率を求めなさい。
ただし3枚の硬貨のそれぞれについて、表と裏の出方は同様に確からしいとする。
⑨右の図は底面の半径が$3cm$、側面になるおうぎ形の半径が$5cm$の円錐の展開図である。
これを組み立ててできる円錐の体積を求めなさい。
【高校受験対策/数学】死守71

単元:
#数学(中学生)#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#比例・反比例#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守71
①$8÷4+6$を計算せよ。
②$\frac{1}{2}+\frac{9}{10}×\frac{5}{3}$を計算せよ。
④$y$は$x$に反比例し、$x=2$のとき$y=-3$である。
このとき、$y$を$x$の式で表せ。
⑤次の比例式で、$x$の値を求めよ。
$x:(4x-1)=1:x$
⑥$\sqrt{7}$より大きく$\sqrt{31}$より小さい整数をすべて書け。
⑦3つの数$a$、$b$、$c$について、$ab \lt 0$、$abc \gt 0$のとき、$a$、$b$、$c$の符号の組み合わせとして、
最も適当なものを下のア~エの中から1つ選び、記号で答えよ。
※図は動画参照
⑧次のように、1から6までの数字がくり返し並んでいる。
左から100番目の数字は何か。
1、2、3、4、5、6、1、2、3、4、5、6、1、2・・・
⑨右の図のように、$AB=AC$である。
二等辺三角形$ABC$と、頂点$A$、$C$をそれぞれ通る2本の平行な直線$l$、$m$がある。
このときの$\angle x$大きさは何度か。
この動画を見る
高校受験対策・死守71
①$8÷4+6$を計算せよ。
②$\frac{1}{2}+\frac{9}{10}×\frac{5}{3}$を計算せよ。
④$y$は$x$に反比例し、$x=2$のとき$y=-3$である。
このとき、$y$を$x$の式で表せ。
⑤次の比例式で、$x$の値を求めよ。
$x:(4x-1)=1:x$
⑥$\sqrt{7}$より大きく$\sqrt{31}$より小さい整数をすべて書け。
⑦3つの数$a$、$b$、$c$について、$ab \lt 0$、$abc \gt 0$のとき、$a$、$b$、$c$の符号の組み合わせとして、
最も適当なものを下のア~エの中から1つ選び、記号で答えよ。
※図は動画参照
⑧次のように、1から6までの数字がくり返し並んでいる。
左から100番目の数字は何か。
1、2、3、4、5、6、1、2、3、4、5、6、1、2・・・
⑨右の図のように、$AB=AC$である。
二等辺三角形$ABC$と、頂点$A$、$C$をそれぞれ通る2本の平行な直線$l$、$m$がある。
このときの$\angle x$大きさは何度か。
【英語】中3-21 仮定法①(基本編)

単元:
#英語(中学生)#中3英語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英語(仮定法①・基本編)
ポイント
仮定法は「もし~ならば」という文で①を使い、動詞を➁形にする。
よくコラボする③(~だろうに)と ④(~できるのに)は覚えておこう!
⑤( ) I ( ) there, I ( ) ( ) a walk every day.
もし私がそこに住んでいたら、毎日散歩するのに。
⑥( ) I ( ) a doctor, I ( ) ( ) sick people.
もし私が医者なら、病気の人々を助けることができるのに。
⑦( ) ( ) ( )a time machine, ( ) would ( ) ( )?
もしあなたがタイムマシーンを持っていたら、あなたは何をするの?
この動画を見る
英語(仮定法①・基本編)
ポイント
仮定法は「もし~ならば」という文で①を使い、動詞を➁形にする。
よくコラボする③(~だろうに)と ④(~できるのに)は覚えておこう!
⑤( ) I ( ) there, I ( ) ( ) a walk every day.
もし私がそこに住んでいたら、毎日散歩するのに。
⑥( ) I ( ) a doctor, I ( ) ( ) sick people.
もし私が医者なら、病気の人々を助けることができるのに。
⑦( ) ( ) ( )a time machine, ( ) would ( ) ( )?
もしあなたがタイムマシーンを持っていたら、あなたは何をするの?
【英語】中3-22 仮定法②(wish編)

単元:
#英語(中学生)#中3英語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英語(仮定法②・wish編)
ポイント
I wish (that)+主語+過去形で①という意味になる。
➁I ( ) I ( ) my own computer.
自分のコンピュータを持っていたらいいのに。
③I ( ) ( ) rich.
私がお金持ちだったらいいのに。
④I ( ) my ( ) teacher ( ) ( ) us homework.
私の先生、私たちに宿題を出さなければいいのに。
⑤I ( ) I ( ) ( ) the piano.
ピアノがひけたらいいのに。
⑥( )
毎日買い物に行けたらいいのに。
この動画を見る
英語(仮定法②・wish編)
ポイント
I wish (that)+主語+過去形で①という意味になる。
➁I ( ) I ( ) my own computer.
自分のコンピュータを持っていたらいいのに。
③I ( ) ( ) rich.
私がお金持ちだったらいいのに。
④I ( ) my ( ) teacher ( ) ( ) us homework.
私の先生、私たちに宿題を出さなければいいのに。
⑤I ( ) I ( ) ( ) the piano.
ピアノがひけたらいいのに。
⑥( )
毎日買い物に行けたらいいのに。
【理科】中3-31.7 エネルギーの有効利用

単元:
#理科(中学生)#物理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
理科(エネルギーの有効利用)
太陽光や風力、木片や落ち葉といった①生物資源( )などの枯渇することのないエネルギーを②エネルギーという。ちなみに①は燃やしても二酸化炭素の増加につながらない、という考え方を③という。
増加につながらない理由は④。
他にも、天然ガスなどの燃料によって発電し、そのときに出る余分な熱を暖房や給湯などに再利用する⑤システムや地域で使う電力や熱などのエネルギーをその地域でつくり出し、たくわえながらかしこく利用しようとする⑥というとり組みも全国各地で進められている。
この動画を見る
理科(エネルギーの有効利用)
太陽光や風力、木片や落ち葉といった①生物資源( )などの枯渇することのないエネルギーを②エネルギーという。ちなみに①は燃やしても二酸化炭素の増加につながらない、という考え方を③という。
増加につながらない理由は④。
他にも、天然ガスなどの燃料によって発電し、そのときに出る余分な熱を暖房や給湯などに再利用する⑤システムや地域で使う電力や熱などのエネルギーをその地域でつくり出し、たくわえながらかしこく利用しようとする⑥というとり組みも全国各地で進められている。
【理科】中3-31.6 エネルギー利用上の課題

単元:
#理科(中学生)#物理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
理科(エネルギー利用上の課題)
石油、石炭、①などの化石燃料や原子力発電に必要な➁は埋蔵量に限りがある。
また化石燃料を燃やすときに発生する二酸化炭素は③化の原因の1つと考えられている。
放射線にはいくつかの種類があるが、その中でもα線は④の原子核の流れ、β線は⑤の流れで、
そのほかにも中性子の流れである⑥線もある。
放射性物質が放射線を出す能力のことを⑦といい、単位は⑧を使う。
また放射線を受けることを⑨といい、人体に対する影響は➉という単位で表される。
この動画を見る
理科(エネルギー利用上の課題)
石油、石炭、①などの化石燃料や原子力発電に必要な➁は埋蔵量に限りがある。
また化石燃料を燃やすときに発生する二酸化炭素は③化の原因の1つと考えられている。
放射線にはいくつかの種類があるが、その中でもα線は④の原子核の流れ、β線は⑤の流れで、
そのほかにも中性子の流れである⑥線もある。
放射性物質が放射線を出す能力のことを⑦といい、単位は⑧を使う。
また放射線を受けることを⑨といい、人体に対する影響は➉という単位で表される。
【理科】中3-31.5 熱の移動
単元:
#理科(中学生)#物理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
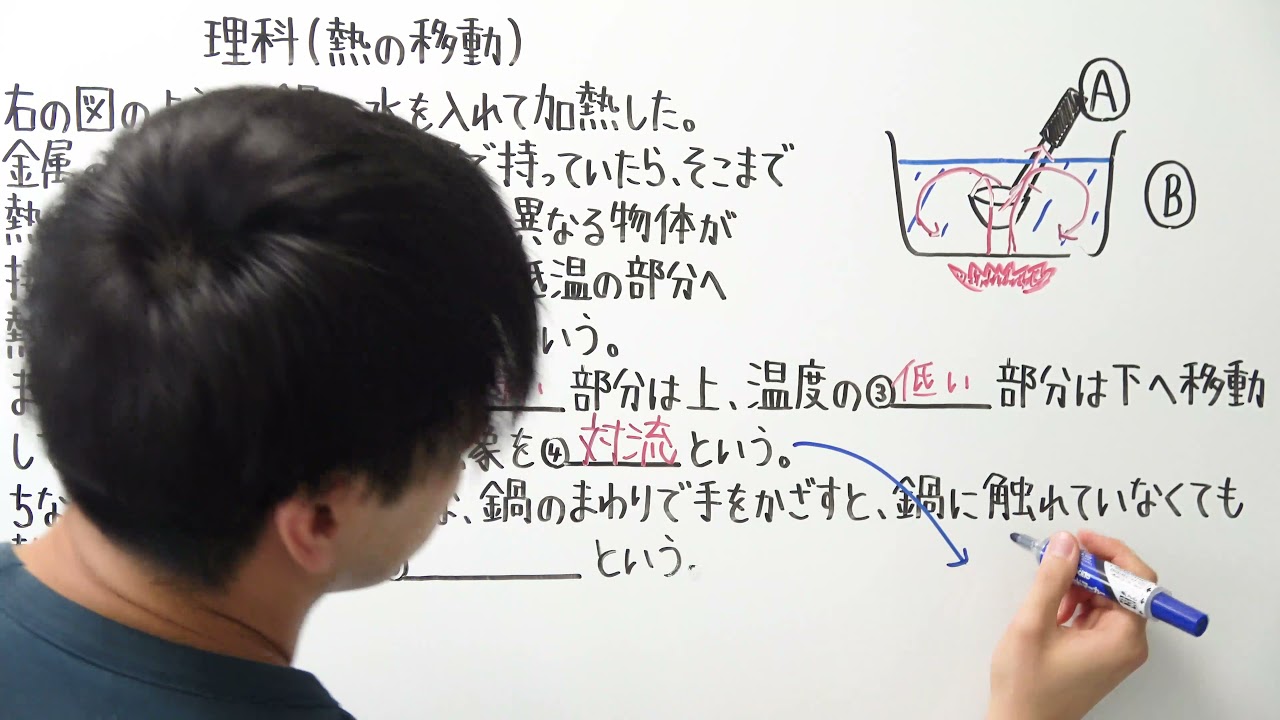
理科(熱の移動)
右の図のように、鍋に水を入れて加熱した。
金属の玉じゃくしをAの位置で持っていたら、そこまで 熱くなってきた。
このように、温度の異なる物体が接しているときの高温の部分から低温の部分へ熱が伝わる現象を①という。
また、鍋の中の水は温度が②部分は上、温度の③部分は下へ移動して全体があたたまる。
この現象を④という。
ちなみに、Bの位置のような、鍋のまわりで手をかざすと、鍋に触れていなくても 熱く感じる。
この現象を⑤という。
この動画を見る
理科(熱の移動)
右の図のように、鍋に水を入れて加熱した。
金属の玉じゃくしをAの位置で持っていたら、そこまで 熱くなってきた。
このように、温度の異なる物体が接しているときの高温の部分から低温の部分へ熱が伝わる現象を①という。
また、鍋の中の水は温度が②部分は上、温度の③部分は下へ移動して全体があたたまる。
この現象を④という。
ちなみに、Bの位置のような、鍋のまわりで手をかざすと、鍋に触れていなくても 熱く感じる。
この現象を⑤という。
【理科】中2-45.5 放射線の発見とその利用

単元:
#理科(中学生)#物理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
理科(放射線の発見とその利用)
1895年、ドイツのレントゲンは実験中に放電管から目に見えない何かが出ているのを発見し、これを①線と名づけた。
その翌年、フランスのベクレルが、ウランから①線に似た目に見えない②線が出ていることを発見した。
ウランのように➁線を出す物質を③物質という。
➁線には①線の他に、α線、β線、γ線などがあり、それぞれ物質を④する性質があり、その性質は⑤などにも使われている。
この動画を見る
理科(放射線の発見とその利用)
1895年、ドイツのレントゲンは実験中に放電管から目に見えない何かが出ているのを発見し、これを①線と名づけた。
その翌年、フランスのベクレルが、ウランから①線に似た目に見えない②線が出ていることを発見した。
ウランのように➁線を出す物質を③物質という。
➁線には①線の他に、α線、β線、γ線などがあり、それぞれ物質を④する性質があり、その性質は⑤などにも使われている。
【英語】中3-20 後置修飾③(並べかえ編)

単元:
#英語(中学生)#中3英語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英語(後置修飾③・並べ替え)
①舞台の上で踊っている女の子はだれですか。
(the girl is on the stage who dancing)?
②あれはアメリカ製のカメラです。
(in that a camera made. America is).
③ケンはとても早く走る犬を飼っています。
(very a dog which fast Ken runs has).
④私が訪れたい場所はハワイです。
(visit Hawaii the place want is I).
この動画を見る
英語(後置修飾③・並べ替え)
①舞台の上で踊っている女の子はだれですか。
(the girl is on the stage who dancing)?
②あれはアメリカ製のカメラです。
(in that a camera made. America is).
③ケンはとても早く走る犬を飼っています。
(very a dog which fast Ken runs has).
④私が訪れたい場所はハワイです。
(visit Hawaii the place want is I).
【英語】中3-19 後置修飾②(接触節編)

単元:
#英語(中学生)#中3英語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英語(後置修飾➁・接触節編)
ポイント
名刺を後ろから修飾する文を①節という。
キーワードは関係代名詞!!
➁This is the pen( )yesterday.
これは私が昨日買ったペンです。
③The book I ( ) ( ) ( ) ( ) interesting.
先週読んだ本は面白かった。
④Kaori is a girl ( ) ( ) long hair.
カオリは髪の長い女の子です。
⑤These toys ( ) ( ) Japan ( ) popular.
日本製のこれらのおもちゃは人気がある。
この動画を見る
英語(後置修飾➁・接触節編)
ポイント
名刺を後ろから修飾する文を①節という。
キーワードは関係代名詞!!
➁This is the pen( )yesterday.
これは私が昨日買ったペンです。
③The book I ( ) ( ) ( ) ( ) interesting.
先週読んだ本は面白かった。
④Kaori is a girl ( ) ( ) long hair.
カオリは髪の長い女の子です。
⑤These toys ( ) ( ) Japan ( ) popular.
日本製のこれらのおもちゃは人気がある。
【英語】中3-18 後置修飾①(基本編)

単元:
#英語(中学生)#中3英語
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英語(後置修飾①・基本編)
ポイント
①詞を修飾する語句や文が①詞の後ろに置かれる。これが後置修飾!
現在分詞(~ing)で➁、過去分詞で③という意味だよ。
④I know the ( ) ( ) over there.
私は向こうで走っている男の子を知っています。
⑤The ( ) ( ) by the door ( ) Ran.
ドアのそばに立っている女の子はランです。
⑥( ) ( ) the ( ) ( ) about Haichi?
葉一について話している男性はだれですか?
⑦She wants a ( ) ( ) in Italy.
彼女はイタリア製のテーブルが欲しい。
⑧I want ( ) ( ) ( ).
何か飲むものが欲しいな。
この動画を見る
英語(後置修飾①・基本編)
ポイント
①詞を修飾する語句や文が①詞の後ろに置かれる。これが後置修飾!
現在分詞(~ing)で➁、過去分詞で③という意味だよ。
④I know the ( ) ( ) over there.
私は向こうで走っている男の子を知っています。
⑤The ( ) ( ) by the door ( ) Ran.
ドアのそばに立っている女の子はランです。
⑥( ) ( ) the ( ) ( ) about Haichi?
葉一について話している男性はだれですか?
⑦She wants a ( ) ( ) in Italy.
彼女はイタリア製のテーブルが欲しい。
⑧I want ( ) ( ) ( ).
何か飲むものが欲しいな。
【英語】中3-3.3 使役動詞と原形不定詞

単元:
#英語(中学生)#中3英語#不定詞(疑問詞+to,It~for to,ask(tell,want)O to,too~to,enough~to,not to)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英語(使役動詞と原形不定詞)
ポイント
使役動詞は主に①という意味で、make、have、letが有名!
➁I ( ) ( ) ( ) his homework.
私は彼に宿題をさせた。
③( ) ( ) ( ) ( ) her computer.
私に彼女のコンピュータを使わせてください。
④This letter ( ) ( ) ( ).
この手紙は私を幸せな気持ちにした。
⑤My sister ( ) ( ) ( ) my room.
私の姉は部屋の掃除を手伝ってくれる。
この動画を見る
英語(使役動詞と原形不定詞)
ポイント
使役動詞は主に①という意味で、make、have、letが有名!
➁I ( ) ( ) ( ) his homework.
私は彼に宿題をさせた。
③( ) ( ) ( ) ( ) her computer.
私に彼女のコンピュータを使わせてください。
④This letter ( ) ( ) ( ).
この手紙は私を幸せな気持ちにした。
⑤My sister ( ) ( ) ( ) my room.
私の姉は部屋の掃除を手伝ってくれる。
【英語】中3-3.2 現在完了進行形

単元:
#英語(中学生)#中3英語#現在完了(継続、経験、完了・結果)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英語(現在完了進行形)
ポイント
have(has) + been + ~ingで①という意味になる。
ただ➁を表す動詞は使えないから注意しよう!
③I ( ) ( ) ( ) English ( ) ( ) ( ).
私は2時間ずっと英語の勉強をしています。
③( ) Masaki ( ) ( ) ( ) music?
マサキはずっと音楽をきいていますか。
⑤Yes, ( ). / No, ( )
⑥She ( ) ( ) ( ) dogs ( )2015.
彼女は2015年からずっと犬を救っています。
⑦( ) ( ) ( ) you ( ) ( ) ( ) him?
どのくらいの間、彼を待ち続けているの?
この動画を見る
英語(現在完了進行形)
ポイント
have(has) + been + ~ingで①という意味になる。
ただ➁を表す動詞は使えないから注意しよう!
③I ( ) ( ) ( ) English ( ) ( ) ( ).
私は2時間ずっと英語の勉強をしています。
③( ) Masaki ( ) ( ) ( ) music?
マサキはずっと音楽をきいていますか。
⑤Yes, ( ). / No, ( )
⑥She ( ) ( ) ( ) dogs ( )2015.
彼女は2015年からずっと犬を救っています。
⑦( ) ( ) ( ) you ( ) ( ) ( ) him?
どのくらいの間、彼を待ち続けているの?
【英語】中3-3.1 現在完了形④・どのくらいの間編

単元:
#英語(中学生)#中3英語#現在完了(継続、経験、完了・結果)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
英語(現在完了形④・どのくらいの間編)
ポイント
「どのくらいの間~していますか」と質問するなら、文頭に①を使おう!
➁( ) ( ) ( ) you ( ) there?
あなたはどのくらいそこに住んでいますか?
③I ( ) ( ) there ( ) ( ) ( ).
2週間です。
④( ) ( ) ( ) ten ( ) ( ).
10歳の時からです。
⑤( ) ( ) ( ) she a headache?
彼女はどのくらいの間頭痛がしているの?
⑥( ) ( ) o'clock ( ) ( ).
昨夜7時からです。
⑦( ) ( ) ( ) ( ) ( ) a teacher?
あなたはどのくらいの間先生をしていますか?
この動画を見る
英語(現在完了形④・どのくらいの間編)
ポイント
「どのくらいの間~していますか」と質問するなら、文頭に①を使おう!
➁( ) ( ) ( ) you ( ) there?
あなたはどのくらいそこに住んでいますか?
③I ( ) ( ) there ( ) ( ) ( ).
2週間です。
④( ) ( ) ( ) ten ( ) ( ).
10歳の時からです。
⑤( ) ( ) ( ) she a headache?
彼女はどのくらいの間頭痛がしているの?
⑥( ) ( ) o'clock ( ) ( ).
昨夜7時からです。
⑦( ) ( ) ( ) ( ) ( ) a teacher?
あなたはどのくらいの間先生をしていますか?
【数学】中2-88 箱ひげ図②(読み取り編)

単元:
#数学(中学生)#中1数学#資料の活用
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数学(箱ひげ図②・読み取り編)
Q.
右の2つの箱ひげ図は、Aグループ15人とBグループ15人のテストの得点を表したものです。
この箱ひげ図から読み取れることとして、次の①~④は正しいといえますか。
「正しい」「正しくない」「このデータからはわからない」のどれかで答えなさい。
①Bグループの平均値は6点である。
②どちらのグループも、半分以上の生徒が5点以上である。
③Aグループは7点以上の人が4人いる。
④範囲も四分位範囲もBグループの方が大きい。
この動画を見る
数学(箱ひげ図②・読み取り編)
Q.
右の2つの箱ひげ図は、Aグループ15人とBグループ15人のテストの得点を表したものです。
この箱ひげ図から読み取れることとして、次の①~④は正しいといえますか。
「正しい」「正しくない」「このデータからはわからない」のどれかで答えなさい。
①Bグループの平均値は6点である。
②どちらのグループも、半分以上の生徒が5点以上である。
③Aグループは7点以上の人が4人いる。
④範囲も四分位範囲もBグループの方が大きい。


