 とある男が授業をしてみた
とある男が授業をしてみた
 とある男が授業をしてみた
とある男が授業をしてみた
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【社会】 地理-75 北海道①

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
北部には①____山地、南部には②____山脈が走り西部には③____平野、東部には④____平野や根釧台地が広がっている。
⑤____帯に属する北海道の特色は、気温と湿度が低く、⑥____がないことだが、南北にのびる山地によって気候の特色が変わる。
日本海側では、冬になると北西の⑦____風が、暖流(対馬海流)の影響で多くの湿気をふくみ、山地にあたり雪をもたらす。
一方、太平洋側では、夏の南東の⑦‗‗‗‗‗‗‗‗‗‗風が寒流の親潮(千島海流)の影響を受けて冷やされ、⑧____が発生するため、夏でも晴天の日が少ない。
この動画を見る
北部には①____山地、南部には②____山脈が走り西部には③____平野、東部には④____平野や根釧台地が広がっている。
⑤____帯に属する北海道の特色は、気温と湿度が低く、⑥____がないことだが、南北にのびる山地によって気候の特色が変わる。
日本海側では、冬になると北西の⑦____風が、暖流(対馬海流)の影響で多くの湿気をふくみ、山地にあたり雪をもたらす。
一方、太平洋側では、夏の南東の⑦‗‗‗‗‗‗‗‗‗‗風が寒流の親潮(千島海流)の影響を受けて冷やされ、⑧____が発生するため、夏でも晴天の日が少ない。
【国語】 文法-39 助動詞②

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
助動詞「せる」「せる」は①____(他の ものに何かをさせる)の意味があり、 動詞の未然形に接続する。
◎次の文中の助動詞「せる」「させる」に ――を書こう。
② カバンをおろさせる。
③ それについて見せるか、聞かせるか 迷っている。
④ 活用の表を完成させよう。
[未,用,終,体,仮,命]
せる せる せろ/せよ
させる させる させろ/させよ
れる れる れろ/れよ
られる られる られろ/られよ
※可能・自発・尊敬の場合は命令形がない。
この動画を見る
助動詞「せる」「せる」は①____(他の ものに何かをさせる)の意味があり、 動詞の未然形に接続する。
◎次の文中の助動詞「せる」「させる」に ――を書こう。
② カバンをおろさせる。
③ それについて見せるか、聞かせるか 迷っている。
④ 活用の表を完成させよう。
[未,用,終,体,仮,命]
せる せる せろ/せよ
させる させる させろ/させよ
れる れる れろ/れよ
られる られる られろ/られよ
※可能・自発・尊敬の場合は命令形がない。
【国語】 国語-38 助動詞①

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
[ポイント]
助動詞「れる」「られる」は、受け身・可能・自発・尊敬の四つの意味があり、動詞の未然形に接続する。
◎次の文中の助動詞「れる」「られる」に ――を書き、その意味を[ポイント]の四つの中から選ぼう。
①友達に写真を見られる。(________)
②先生が手紙を書かれる。(________)
③彼は何でも食べられる。(________)
④幼いころが思い出される。(________)
⑤彼女は早く起きられる。(________)
◎みんなから笑われる。(________)
◎兄に本を取られる。(________)
⑧校長先生が授業をされる。(________)
この動画を見る
[ポイント]
助動詞「れる」「られる」は、受け身・可能・自発・尊敬の四つの意味があり、動詞の未然形に接続する。
◎次の文中の助動詞「れる」「られる」に ――を書き、その意味を[ポイント]の四つの中から選ぼう。
①友達に写真を見られる。(________)
②先生が手紙を書かれる。(________)
③彼は何でも食べられる。(________)
④幼いころが思い出される。(________)
⑤彼女は早く起きられる。(________)
◎みんなから笑われる。(________)
◎兄に本を取られる。(________)
⑧校長先生が授業をされる。(________)
【はいちのだらだラジオ】 第78回 - 平成26年度 卒業式

【国語】 文法-37 助詞④

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
主に文の終わりに付いて、話し手の気持ちなどを表す助詞を終助詞という。
◎次の文の終助詞に――を書こう。
①その本を読むな。
②いっしょに行こうね。
③弟よ、がんばってくれ。
④それを貸してくれないかしら。
⑤次の――線部の中で、同じ意味・用法のものを二つ選ぼう。
※下線部は動画内参照
㋐彼女も行くだろうか。
㋑なるほど、そうだったのか。
㋒そんなことがあるものか。
㋓これは彼が書いたのですが。
この動画を見る
主に文の終わりに付いて、話し手の気持ちなどを表す助詞を終助詞という。
◎次の文の終助詞に――を書こう。
①その本を読むな。
②いっしょに行こうね。
③弟よ、がんばってくれ。
④それを貸してくれないかしら。
⑤次の――線部の中で、同じ意味・用法のものを二つ選ぼう。
※下線部は動画内参照
㋐彼女も行くだろうか。
㋑なるほど、そうだったのか。
㋒そんなことがあるものか。
㋓これは彼が書いたのですが。
【国語】 文法-36 助詞③

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
いろいろな語に付いて意味を付け加える助詞を副助詞という。
◎次の文の副助詞に―――を書こう。
①私は桃もみかんも好きです。
②これさえあればよい。
③外ばかり見ている。
②子どもでも知っている。
⑤服やスカートなどを買う。
⑥三十分くらい会って話した。
⑦一つだけしかくれなかった。
⑧次こそ負けない。
⑨行くか行かないかを決めなさい。
この動画を見る
いろいろな語に付いて意味を付け加える助詞を副助詞という。
◎次の文の副助詞に―――を書こう。
①私は桃もみかんも好きです。
②これさえあればよい。
③外ばかり見ている。
②子どもでも知っている。
⑤服やスカートなどを買う。
⑥三十分くらい会って話した。
⑦一つだけしかくれなかった。
⑧次こそ負けない。
⑨行くか行かないかを決めなさい。
【社会】 地理-74 東北地方④

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\boxed{ E }$①____
県中央には②____山地がある。
青森県との県境には③____山地があり、ブナの原生林が残り世界遺産に登録されている。
また、④____平野では稲作が盛ん。
$\boxed{ F }$⑤____
県中央を⑥____川が流れ、その河口には⑦____平野があり、稲作が盛んにおこなわ れている。
また、山形盆地などでは果実栽培が盛んで、特に⑧____の生産が有名。
この動画を見る
$\boxed{ E }$①____
県中央には②____山地がある。
青森県との県境には③____山地があり、ブナの原生林が残り世界遺産に登録されている。
また、④____平野では稲作が盛ん。
$\boxed{ F }$⑤____
県中央を⑥____川が流れ、その河口には⑦____平野があり、稲作が盛んにおこなわ れている。
また、山形盆地などでは果実栽培が盛んで、特に⑧____の生産が有名。
【はいちのだらだラジオ】 第77回 - 30歳になりました!

【社会】 地理-73 東北地方③

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\boxed{ C }$①____
東部には②____高地があり、三陸海岸の南部は海岸線が複雑な③____海岸として有名。
また、④____寺のある平泉は世界遺産に登録されている。
$\boxed{ D }$____
2つの半島(⑥____半島、⑦____半島)があり、 りんごの生産が盛ん。
また、津軽塗りは⑧______品に指定されている。
この動画を見る
$\boxed{ C }$①____
東部には②____高地があり、三陸海岸の南部は海岸線が複雑な③____海岸として有名。
また、④____寺のある平泉は世界遺産に登録されている。
$\boxed{ D }$____
2つの半島(⑥____半島、⑦____半島)があり、 りんごの生産が盛ん。
また、津軽塗りは⑧______品に指定されている。
【国語】 文法-35 助詞②

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
接続の関係を示す助詞を接続助詞という。
◎次の文の接続助詞に――を書き、その接続の関係を順接・逆接・並立から選ぼう。
①新しいから、きれいだ。(________)
②並んだけれど、買えなかった。(________)
③優しいし、かっこいい。(________)
④調べても、わからない。(________)
⑤行ったのに、会えなかった。(________)
⑥荷物が重くて持てない。(________)
⑦安くておいしい。(________)
⑧そこに着くと、彼がいた。(________)
この動画を見る
接続の関係を示す助詞を接続助詞という。
◎次の文の接続助詞に――を書き、その接続の関係を順接・逆接・並立から選ぼう。
①新しいから、きれいだ。(________)
②並んだけれど、買えなかった。(________)
③優しいし、かっこいい。(________)
④調べても、わからない。(________)
⑤行ったのに、会えなかった。(________)
⑥荷物が重くて持てない。(________)
⑦安くておいしい。(________)
⑧そこに着くと、彼がいた。(________)
【社会】 地理-72 東北地方②

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\boxed{ A }$①____
漆器や酒造りなどの②____産業が盛んで、会津塗は国から③________ 品として指定されている。
また、きれいな水を利用した電子部品、 精密機械などの工業が発達している。
$\boxed{ B }$④____
政令指定都市である⑤____市は東北地方の行政の中心となる⑥____都市である。
また、稲作が盛んな⑦____平野がある。
この動画を見る
$\boxed{ A }$①____
漆器や酒造りなどの②____産業が盛んで、会津塗は国から③________ 品として指定されている。
また、きれいな水を利用した電子部品、 精密機械などの工業が発達している。
$\boxed{ B }$④____
政令指定都市である⑤____市は東北地方の行政の中心となる⑥____都市である。
また、稲作が盛んな⑦____平野がある。
【はいちのだらだラジオ】 第76回 - 受験お疲れ様でした!

【社会】 地理-71 東北地方①

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
東北地方の中央には①____山脈が走り、 その西側には②____山地、東側には③____高地がある。
日本海側の夏は、晴天の日が多く、気温も高くなるが、冬になると北西の④____風と⑤____海流の影響で多くの雪が降る。
太平洋側は、冬の積雪量は少ないが、夏になると寒流の⑥ ____の影響を受け、冷たく湿った北東の風(⑨____) がふき、稲作などの農業に被害をおよぼす⑩____害をもたらす。
この動画を見る
東北地方の中央には①____山脈が走り、 その西側には②____山地、東側には③____高地がある。
日本海側の夏は、晴天の日が多く、気温も高くなるが、冬になると北西の④____風と⑤____海流の影響で多くの雪が降る。
太平洋側は、冬の積雪量は少ないが、夏になると寒流の⑥ ____の影響を受け、冷たく湿った北東の風(⑨____) がふき、稲作などの農業に被害をおよぼす⑩____害をもたらす。
【国語】 文法-34 助詞①
単元:
#国語(中学生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
助詞は①____語で活用が②____。
◎次の文の助詞に――を書こう。
③友達の家から帰る。
④話し合いが九時に始まる。
主に体言に付く助詞を⑤____助詞と言い、⑥________ と覚えよう。
◎次の―――線部の中で同じ意味・用法 のものを二つ選ぼう。
※下線部は動画内参照
㋐黒板の文字が見えない。
㋑車の走る音が聞こえる。
㋒天気の良い日に出かける。
㋓新しいのが欲しい。
この動画を見る
助詞は①____語で活用が②____。
◎次の文の助詞に――を書こう。
③友達の家から帰る。
④話し合いが九時に始まる。
主に体言に付く助詞を⑤____助詞と言い、⑥________ と覚えよう。
◎次の―――線部の中で同じ意味・用法 のものを二つ選ぼう。
※下線部は動画内参照
㋐黒板の文字が見えない。
㋑車の走る音が聞こえる。
㋒天気の良い日に出かける。
㋓新しいのが欲しい。
【社会】 地理-70 関東地方④
単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
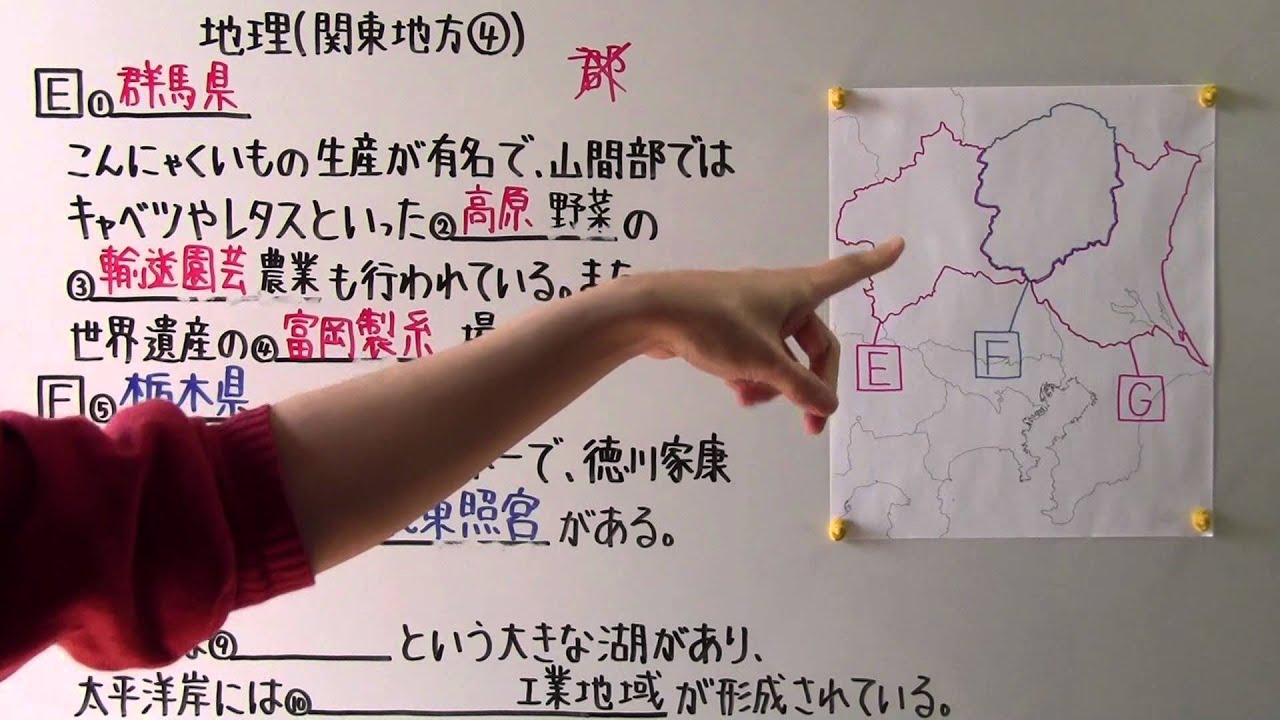
$\boxed{ E }$①____
こんにゃくいもの生産が有名で、山間部ではキャベツやレタスといった②____野菜の③____ 農業も行われている。
また、 世界遺産の④______場がある。
$\boxed{ F }$⑤____
⑥____の生産量が日本一で、徳川家康がまつられている⑦____がある。
$\boxed{ G }$⑧____
県南には⑨____という大きな湖があり、太平洋岸には⑩____工業地域が形成されている。
この動画を見る
$\boxed{ E }$①____
こんにゃくいもの生産が有名で、山間部ではキャベツやレタスといった②____野菜の③____ 農業も行われている。
また、 世界遺産の④______場がある。
$\boxed{ F }$⑤____
⑥____の生産量が日本一で、徳川家康がまつられている⑦____がある。
$\boxed{ G }$⑧____
県南には⑨____という大きな湖があり、太平洋岸には⑩____工業地域が形成されている。
【はいちのだらだラジオ】 第75回 - はいちが○○に出ます!

【社会】 地理-69 関東地方③

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\boxed{ C }$①____
県の多くの面積を②____半島が占めていて、 東京湾沿いの埋め立て地帯には③____ 工業地域が形成されている。
また、大消費地に近い条件を生かして、都市向けに野菜を出荷する④____農業が行われている。
$\boxed{ D }$⑤____
政令指定都市である⑥____市は、大宮などの3市が合併してできた100万都市である。
また①‗‗‗‗‗‗‗‗‗‗と同じ条件のため④‗‗‗‗‗‗‗‗‗‗農業が盛んで、ねぎなどの生産が多い。
この動画を見る
$\boxed{ C }$①____
県の多くの面積を②____半島が占めていて、 東京湾沿いの埋め立て地帯には③____ 工業地域が形成されている。
また、大消費地に近い条件を生かして、都市向けに野菜を出荷する④____農業が行われている。
$\boxed{ D }$⑤____
政令指定都市である⑥____市は、大宮などの3市が合併してできた100万都市である。
また①‗‗‗‗‗‗‗‗‗‗と同じ条件のため④‗‗‗‗‗‗‗‗‗‗農業が盛んで、ねぎなどの生産が多い。
【国語】 文法-33 形容動詞②

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
国語(形容動詞)
形容動詞の活用は二種類。
次の表を完成させよう。
例語,語幹:[未,用,終,体,仮,命]
静かだ,静か だ 〇
静かです,静か です です 〇 〇
続き方:
う た,ない,なる × とき,ので, ば ×
◎次の―――線部の形容動詞の活用形を書こう。
※下線部は動画内参照
①彼はいっも元気です。
②彼女のことが心配になる。(________形)
③きれいなのは、あの絵だ。(________形)
④娘のことが心配でしょう。(________形)
この動画を見る
国語(形容動詞)
形容動詞の活用は二種類。
次の表を完成させよう。
例語,語幹:[未,用,終,体,仮,命]
静かだ,静か だ 〇
静かです,静か です です 〇 〇
続き方:
う た,ない,なる × とき,ので, ば ×
◎次の―――線部の形容動詞の活用形を書こう。
※下線部は動画内参照
①彼はいっも元気です。
②彼女のことが心配になる。(________形)
③きれいなのは、あの絵だ。(________形)
④娘のことが心配でしょう。(________形)
【国語】 文法-32 形容動詞①

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
形容動詞は①____語で活用が②____。
終止形が③「____」「____」で終わる。
◎次の―――線部の形容動詞の 終止形を書こう。
※下線部は動画内参照
④パソコンがさらに便利になる。(________)
⑤その問題は簡単でした。(________)
◎次の――線部は文中で主語·述語·連体修飾語·連用修飾語·接続語のうちのどの働きをしている?
⑥くっをきれいに洗う。(________語)
⑦きれいな字を書く。(________語)
⑧彼女はとても親切だ。(________語)
⑨好きなのは、この曲だ。(________語)
⑩きれいなので、持って帰ろう。(________語)
この動画を見る
形容動詞は①____語で活用が②____。
終止形が③「____」「____」で終わる。
◎次の―――線部の形容動詞の 終止形を書こう。
※下線部は動画内参照
④パソコンがさらに便利になる。(________)
⑤その問題は簡単でした。(________)
◎次の――線部は文中で主語·述語·連体修飾語·連用修飾語·接続語のうちのどの働きをしている?
⑥くっをきれいに洗う。(________語)
⑦きれいな字を書く。(________語)
⑧彼女はとても親切だ。(________語)
⑨好きなのは、この曲だ。(________語)
⑩きれいなので、持って帰ろう。(________語)
【国語】 文法-31 形容詞②

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
国語(形容詞)
形容詞の活用は一種類だけ。
◎次の表を完成させよう。
語幹:[未,用,終,体,仮,命]
美し い 〇
白 い 〇
続き方:
う,た,なる,ざいます × もの,ば ×
◎次の――線部の形容詞の活用形を書こう。
※下線部は動画内参照
①彼に会えてうれしい。 (________形)
②うれしい結果だった。 (________形)
③昨日はとても寒かった。 (________形)
④寒ければ、上着を着なさい。 (________形)
この動画を見る
国語(形容詞)
形容詞の活用は一種類だけ。
◎次の表を完成させよう。
語幹:[未,用,終,体,仮,命]
美し い 〇
白 い 〇
続き方:
う,た,なる,ざいます × もの,ば ×
◎次の――線部の形容詞の活用形を書こう。
※下線部は動画内参照
①彼に会えてうれしい。 (________形)
②うれしい結果だった。 (________形)
③昨日はとても寒かった。 (________形)
④寒ければ、上着を着なさい。 (________形)
【国語】 文法-30 形容詞①

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
形容詞は①____語で活用が②____。
終止形が③「____」で終わる。
◎次の――線部の形容詞の終止形を書こう。
※下線部は動画内参照
④勝ってうれしかった。(________)
⑤重ければ、代わりに持つよ。(________)
次の――線部は、文中で主語·述語·連体修飾語·連用修飾語·接続語のうちのどの働きをしている?
※下線部は動画内参照
⑥うれしいので、笑ってしまう。(________語)
⑦美しい女性がいる。(________語)
⑧彼女は美しくおどる。(________語)
⑨風がすずしい。(________語)
⑩強いのは、あのチームだ。(________語)
この動画を見る
形容詞は①____語で活用が②____。
終止形が③「____」で終わる。
◎次の――線部の形容詞の終止形を書こう。
※下線部は動画内参照
④勝ってうれしかった。(________)
⑤重ければ、代わりに持つよ。(________)
次の――線部は、文中で主語·述語·連体修飾語·連用修飾語·接続語のうちのどの働きをしている?
※下線部は動画内参照
⑥うれしいので、笑ってしまう。(________語)
⑦美しい女性がいる。(________語)
⑧彼女は美しくおどる。(________語)
⑨風がすずしい。(________語)
⑩強いのは、あのチームだ。(________語)
【国語】 文法-29 動詞の活用③

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
○○活用を調べるときは、 その動詞に「ない」を付けよう。
◎次の動詞の活用の種類を書こう。
話す(________活用)
②切れる(________活用)
③降りる(________活用)
④する(________活用)
⑤来る(________活用)
⑥集める(________活用)
⑦書く(________活用)
⑧旅行する(________活用)
⑨当てる(________活用)
⑩いる(________活用)
⑪学ぶ(________活用)
⑫運ぶ(________活用)
⑬起きる(________活用)
この動画を見る
○○活用を調べるときは、 その動詞に「ない」を付けよう。
◎次の動詞の活用の種類を書こう。
話す(________活用)
②切れる(________活用)
③降りる(________活用)
④する(________活用)
⑤来る(________活用)
⑥集める(________活用)
⑦書く(________活用)
⑧旅行する(________活用)
⑨当てる(________活用)
⑩いる(________活用)
⑪学ぶ(________活用)
⑫運ぶ(________活用)
⑬起きる(________活用)
【社会】 地理-68 関東地方②

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\boxed{ A }$①____
首都である東京には、国会議事堂や最高裁判所など日本を動かす②____機能が集中している。
また、東京を中心とする③____圏では④第____次産業
が発達している。
しかし、地価が高く、住宅問題やごみ問題などの都市問題をかかえている。
東京湾の臨海部には⑤____工業地帯が広がる。
$\boxed{ B }$⑥____
3つの⑦____都市(横浜市、川崎市、相模原市)がある。
工業原料の輸入に適した臨海部には、火力発電所や大工場が立ち並んでいる。
この動画を見る
$\boxed{ A }$①____
首都である東京には、国会議事堂や最高裁判所など日本を動かす②____機能が集中している。
また、東京を中心とする③____圏では④第____次産業
が発達している。
しかし、地価が高く、住宅問題やごみ問題などの都市問題をかかえている。
東京湾の臨海部には⑤____工業地帯が広がる。
$\boxed{ B }$⑥____
3つの⑦____都市(横浜市、川崎市、相模原市)がある。
工業原料の輸入に適した臨海部には、火力発電所や大工場が立ち並んでいる。
【はいちのだらだラジオ】 第74回 - 大人の言うことはきくべき?

【国語】 文法-28 動詞の活用②

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
動詞を活用させたとき、
①____部分を語幹といい、
②____部分を活用語尾という。
◎次の表を完成させよう。
語幹:[未,用,終,体,仮,命]
話す:はな そ さ す せ せ
落ちる:ち ちる ちる ちろ ちよ
書く:い き
続き方:
ない,ます,う,た × とき,こと,ば × ば
また、連用形が「た,て」などに続くとき、もとの行にはない音になることがある。
これを音便形といい、「書いた」など の③____音便、「行った」などの④____ 音便、 「読んだ」などの⑤____ 音使の三つの種類がある。
この動画を見る
動詞を活用させたとき、
①____部分を語幹といい、
②____部分を活用語尾という。
◎次の表を完成させよう。
語幹:[未,用,終,体,仮,命]
話す:はな そ さ す せ せ
落ちる:ち ちる ちる ちろ ちよ
書く:い き
続き方:
ない,ます,う,た × とき,こと,ば × ば
また、連用形が「た,て」などに続くとき、もとの行にはない音になることがある。
これを音便形といい、「書いた」など の③____音便、「行った」などの④____ 音便、 「読んだ」などの⑤____ 音使の三つの種類がある。
【社会】 地理-67 関東地方①

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
関東地方の面積の約半分を日本最大の①____平野がしめている。
また、流域面積が日本最大の②____川が流れ、台地は火山灰が堆積した赤土(③______)におおわれていて、多くが畑作地帯となっている。
冬は乾燥し、 ④____と呼ばれる冷たい北西の風がふく。
また、東京や横浜などの大都市では、都市部の気温が周辺部よりも高くなる⑤____現象が見られる。
この動画を見る
関東地方の面積の約半分を日本最大の①____平野がしめている。
また、流域面積が日本最大の②____川が流れ、台地は火山灰が堆積した赤土(③______)におおわれていて、多くが畑作地帯となっている。
冬は乾燥し、 ④____と呼ばれる冷たい北西の風がふく。
また、東京や横浜などの大都市では、都市部の気温が周辺部よりも高くなる⑤____現象が見られる。
【国語】 文法-27 動詞の活用①

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎六種類の動詞の活用
$\boxed{ 1 }$
____形……まだ起こっていない。
(例)落ちない・話そう・捨てよう 行かせる・求められる
$\boxed{ 2 }$
____形
(例)帰りたい・受けた・落ちて 起きます
$\boxed{ 3 }$
____形……言い切り。
(例)話すと・行くから・するけれど
$\boxed{ 4 }$
____形……体言に続く。
(例)行く人・泣くので・勉強するのに 着るのは
$\boxed{ 5 }$
____形……仮にそうしておく。
(例)見れば・行けば
$\boxed{ 6 }$
____形
(例)話せ・見ろ・見よ・しろ・せよ
この動画を見る
◎六種類の動詞の活用
$\boxed{ 1 }$
____形……まだ起こっていない。
(例)落ちない・話そう・捨てよう 行かせる・求められる
$\boxed{ 2 }$
____形
(例)帰りたい・受けた・落ちて 起きます
$\boxed{ 3 }$
____形……言い切り。
(例)話すと・行くから・するけれど
$\boxed{ 4 }$
____形……体言に続く。
(例)行く人・泣くので・勉強するのに 着るのは
$\boxed{ 5 }$
____形……仮にそうしておく。
(例)見れば・行けば
$\boxed{ 6 }$
____形
(例)話せ・見ろ・見よ・しろ・せよ
【国語】 文法-26 動詞②

単元:
#国語(中学生)#文法
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎四種類の動詞
$\boxed{ 1 }$
動詞……「何を」という対象が必要
(例)集める・変える・書く
$\boxed{ 2 }$
動詞……「何を」を必要としない
(例)集まる・変わる・来る
$\boxed{ 3 }$
動詞……「~できる」という意味を表す
(例)読める・行ける・買える
$\boxed{ 4 }$
補助動詞……笑っている・置いておく・飲んでみる・変えていく
◎次の文の―の動詞の種類を書こう。
①部屋のドアを閉める。 (________動詞)
②彼は英語を話せる。(________動詞)
③ 会議が始まる。(________動詞)
④大きな鳥が飛んでいる。(________動詞)
この動画を見る
◎四種類の動詞
$\boxed{ 1 }$
動詞……「何を」という対象が必要
(例)集める・変える・書く
$\boxed{ 2 }$
動詞……「何を」を必要としない
(例)集まる・変わる・来る
$\boxed{ 3 }$
動詞……「~できる」という意味を表す
(例)読める・行ける・買える
$\boxed{ 4 }$
補助動詞……笑っている・置いておく・飲んでみる・変えていく
◎次の文の―の動詞の種類を書こう。
①部屋のドアを閉める。 (________動詞)
②彼は英語を話せる。(________動詞)
③ 会議が始まる。(________動詞)
④大きな鳥が飛んでいる。(________動詞)
【社会】 地理-66 中部地方⑤

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\boxed{ H }$①____ 県
南部には②____ 工業地域が広がり、特に浜松市は自動車工業や楽器が有名。
また、③____ の産地としても有名。
$\boxed{ I }$④____ 県
⑤____ 盆地の中央部には水田地帯が
広がっている。
また、盆地の周辺部の扇状地では⑥____ 栽培が盛んで、大都市への近さを 生かして、ぶどう狩りやもも狩りを行う⑦____ 農園も多い。
この動画を見る
$\boxed{ H }$①____ 県
南部には②____ 工業地域が広がり、特に浜松市は自動車工業や楽器が有名。
また、③____ の産地としても有名。
$\boxed{ I }$④____ 県
⑤____ 盆地の中央部には水田地帯が
広がっている。
また、盆地の周辺部の扇状地では⑥____ 栽培が盛んで、大都市への近さを 生かして、ぶどう狩りやもも狩りを行う⑦____ 農園も多い。
【はいちのだらだラジオ】 第73回 - このチャンネルについて



