 とある男が授業をしてみた
とある男が授業をしてみた
 とある男が授業をしてみた
とある男が授業をしてみた
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【社会】 公民-38 公害の防止と環境の保全

単元:
#社会(中学生)#公民
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
戦後、日本が急速な経済発展をとげるにつれて、各地で深刻な公害が起こった。
なかでも①____病、②____病、③____病、④____は四大公害といわれた。
被害が広がると、公害追放を唱える⑤____が各地で展開され、国も公害対策基本法を制定するなどの対策をとった。
公害防止の努力によって、生産活動による公害は減っていったが、その反面、排気ガスやごみなどの生活公害やダイオキシンなどの新しい公害が問題となった。
そのため、 国は⑥____法を制定し、問題に取り組んでいる。 また、地球規模の環境問題(地球温暖化、さばく化など)への関心が高まっていて、日本の企業も⑦________型の製品の開発に力を注いでいる。
そして、私たち個人も⑧____社会をめざして、ごみを減らす努力をしたり、 リサイクルを意識したりするなどしていかなければならない。
この動画を見る
戦後、日本が急速な経済発展をとげるにつれて、各地で深刻な公害が起こった。
なかでも①____病、②____病、③____病、④____は四大公害といわれた。
被害が広がると、公害追放を唱える⑤____が各地で展開され、国も公害対策基本法を制定するなどの対策をとった。
公害防止の努力によって、生産活動による公害は減っていったが、その反面、排気ガスやごみなどの生活公害やダイオキシンなどの新しい公害が問題となった。
そのため、 国は⑥____法を制定し、問題に取り組んでいる。 また、地球規模の環境問題(地球温暖化、さばく化など)への関心が高まっていて、日本の企業も⑦________型の製品の開発に力を注いでいる。
そして、私たち個人も⑧____社会をめざして、ごみを減らす努力をしたり、 リサイクルを意識したりするなどしていかなければならない。
【社会】 地理-47 日本の農林水産業

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
日本の農業は、北海道を除いて規模の小さい自作農が多い。
野菜の生産は、千葉県や茨城県などの①____農業の地域や、宮崎県や高知県などの暖かい気候を利用した②____栽培の地域、長野県や岩手県などの冷涼な気候を利用した③____栽培を中心にさかんで、温室やビニールハウスを利用した④____農業が発達している地域もある。
農産物の⑤____化により、国内産の農産物は安い輸入農産物におされている。
そのため、日本の⑥____率はおおはばに低下している。
現在の日本の漁業は、漁獲量の制限が厳しくなったため、遠洋漁業や沖合漁業に従事する人が減っている。
また、海外からの輸入も増加しているため、とる漁業から育てる漁業へと方針が変わっており、⑦____漁業や⑧____漁業の成長が期待されている。
この動画を見る
日本の農業は、北海道を除いて規模の小さい自作農が多い。
野菜の生産は、千葉県や茨城県などの①____農業の地域や、宮崎県や高知県などの暖かい気候を利用した②____栽培の地域、長野県や岩手県などの冷涼な気候を利用した③____栽培を中心にさかんで、温室やビニールハウスを利用した④____農業が発達している地域もある。
農産物の⑤____化により、国内産の農産物は安い輸入農産物におされている。
そのため、日本の⑥____率はおおはばに低下している。
現在の日本の漁業は、漁獲量の制限が厳しくなったため、遠洋漁業や沖合漁業に従事する人が減っている。
また、海外からの輸入も増加しているため、とる漁業から育てる漁業へと方針が変わっており、⑦____漁業や⑧____漁業の成長が期待されている。
【社会】 公民-37 社会保障のしくみ

単元:
#社会(中学生)#公民
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
生活が困難になったとき、個人にかわって国が生活の保障を行う制度を①____制度という。
日本の①‗‗‗‗‗‗‗‗‗‗制度は、日本国憲法第25条1項の②____権(すべて国民は、③____で④____的な⑤____ の生活を営む権利を有する)と2項にもとづいて整備されてきて、⑥____、⑦____、⑧____、⑨____の4つを基本的な柱としている。
しかし、少子高齢化が進んでいる日本では、医療費や⑩____
額が増えるのに⑪____が減るため、それらをまかなうための⑫____料と税収が減少していることが問題になっている。
高齢化の進展により、⑬____制度(40歳以上の人が加入し、介護が必要になったときに介護サービスを受けられる)や⑭____
制度(75歳以上の高齢者は独自の保険に加入する)が導入された。
この動画を見る
生活が困難になったとき、個人にかわって国が生活の保障を行う制度を①____制度という。
日本の①‗‗‗‗‗‗‗‗‗‗制度は、日本国憲法第25条1項の②____権(すべて国民は、③____で④____的な⑤____ の生活を営む権利を有する)と2項にもとづいて整備されてきて、⑥____、⑦____、⑧____、⑨____の4つを基本的な柱としている。
しかし、少子高齢化が進んでいる日本では、医療費や⑩____
額が増えるのに⑪____が減るため、それらをまかなうための⑫____料と税収が減少していることが問題になっている。
高齢化の進展により、⑬____制度(40歳以上の人が加入し、介護が必要になったときに介護サービスを受けられる)や⑭____
制度(75歳以上の高齢者は独自の保険に加入する)が導入された。
【はいちのだらだラジオ】 第62回 - ツイッターの画像の答え

【社会】 地理-46 日本の資源とエネルギー

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
日本は山がちで水資源にめぐまれているため、1950年代ごろまでには、山地にダムを建設して、その水を利用した①____発電に電力の多くを依存してきた。
しかし、現在の日本は当時に比べ電力の需要がおおはばに増えたため、石油や石炭、天然ガスを燃料とする②____発電や、ウランを燃料とする③____発電が中心になっている(2011年に発生した東日本大震災より、状況は 大きく変わった)。
だが、②‗‗‗‗‗‗‗‗‗‗発電は、④____の調整がしやすいというメリットが
ある反面、温暖化の原因となる⑤____が発生するというデメリットもある。
また、石油や石炭は有限資源なので、それらにたよる割合を低下させる必要がある。
そして、環境の汚染を少なくするためにも⑥____発電や⑦____発電などの再生可能エネルギーの積極的な利用や、工場や各家庭における⑧____ への意識向上が必要となっている。
この動画を見る
日本は山がちで水資源にめぐまれているため、1950年代ごろまでには、山地にダムを建設して、その水を利用した①____発電に電力の多くを依存してきた。
しかし、現在の日本は当時に比べ電力の需要がおおはばに増えたため、石油や石炭、天然ガスを燃料とする②____発電や、ウランを燃料とする③____発電が中心になっている(2011年に発生した東日本大震災より、状況は 大きく変わった)。
だが、②‗‗‗‗‗‗‗‗‗‗発電は、④____の調整がしやすいというメリットが
ある反面、温暖化の原因となる⑤____が発生するというデメリットもある。
また、石油や石炭は有限資源なので、それらにたよる割合を低下させる必要がある。
そして、環境の汚染を少なくするためにも⑥____発電や⑦____発電などの再生可能エネルギーの積極的な利用や、工場や各家庭における⑧____ への意識向上が必要となっている。
【社会】 公民-36 政府の役割

単元:
#社会(中学生)#公民
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
政府の重要な役割は、市場では供給されにくい公共施設(①____)をつくったり、医療や教育などの②____を提供したり、あるいは社会保障のための支出を行ったりして国民のくらしをよくすることである。
また、景気(国の経済が活発に動いているか、沈滞しているか)を調節することも政府の役割である。
不景気と好景気とは交互にくり返す(③____)ので、それぞれの対応策が必要となる。
不景気のときには、所得も消費も低下し、物価の下落(④____ )が進むため、政府は減税を行ったり、公共事業への支出(⑤____)を増やしたりする。
一方、好景気のときには、物価の上昇(⑥____)が進み、人々の生活を圧迫するので、政府は増税や公共事業の削減をする。
このように、財政の活動を通じて景気の波を調節することを⑦____という。
この動画を見る
政府の重要な役割は、市場では供給されにくい公共施設(①____)をつくったり、医療や教育などの②____を提供したり、あるいは社会保障のための支出を行ったりして国民のくらしをよくすることである。
また、景気(国の経済が活発に動いているか、沈滞しているか)を調節することも政府の役割である。
不景気と好景気とは交互にくり返す(③____)ので、それぞれの対応策が必要となる。
不景気のときには、所得も消費も低下し、物価の下落(④____ )が進むため、政府は減税を行ったり、公共事業への支出(⑤____)を増やしたりする。
一方、好景気のときには、物価の上昇(⑥____)が進み、人々の生活を圧迫するので、政府は増税や公共事業の削減をする。
このように、財政の活動を通じて景気の波を調節することを⑦____という。
【社会】 地理-37 日本の山地と海岸①
単元:
#社会(中学生)#社会(高校生)#地理#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
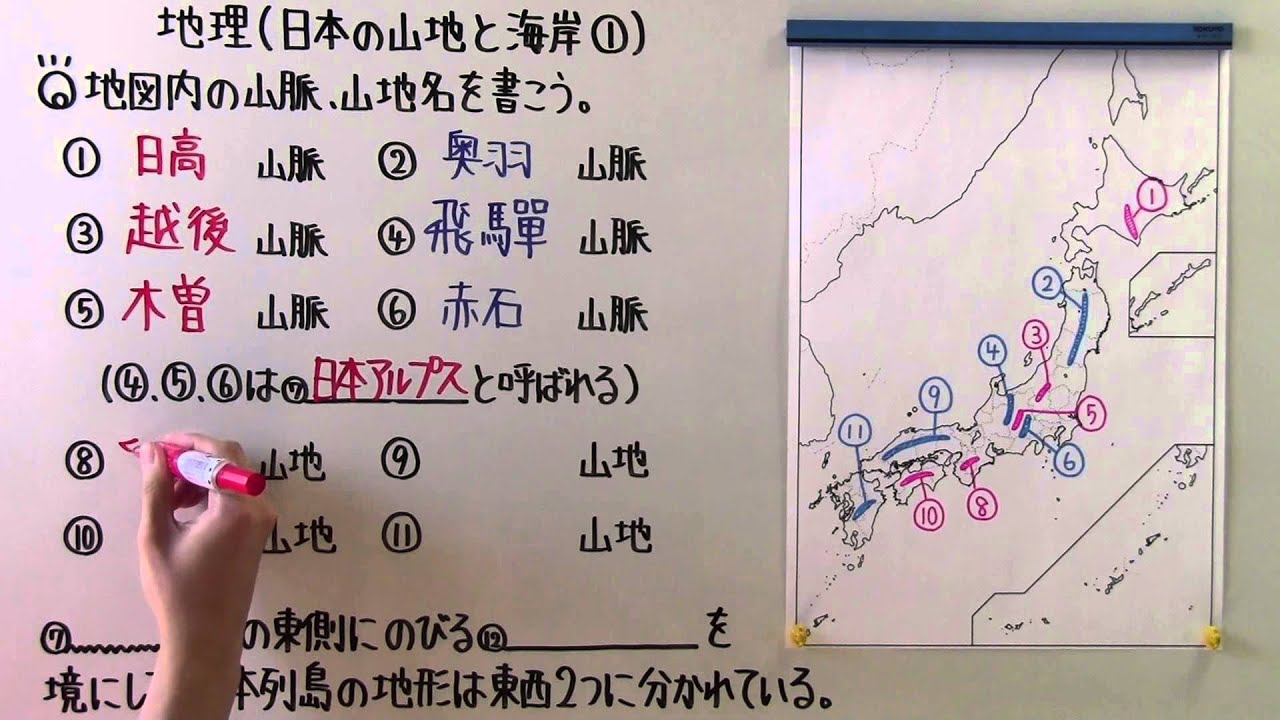
◎地図内の山脈、山地名を書こう。
①____________山脈
②____________山脈
③____________山脈
④____________山脈
⑤____________山脈
⑥____________山脈
(④,⑤,⑥は⑦____と呼ばれる)
⑧____________山地
⑨____________山地
⑩____________山地
⑪____________山地
※地図は動画内参照
⑦‗‗‗‗‗‗‗‗‗‗の東側に伸びる⑫____を境にして、日本列島の地形は東西2つに分かれている。
この動画を見る
◎地図内の山脈、山地名を書こう。
①____________山脈
②____________山脈
③____________山脈
④____________山脈
⑤____________山脈
⑥____________山脈
(④,⑤,⑥は⑦____と呼ばれる)
⑧____________山地
⑨____________山地
⑩____________山地
⑪____________山地
※地図は動画内参照
⑦‗‗‗‗‗‗‗‗‗‗の東側に伸びる⑫____を境にして、日本列島の地形は東西2つに分かれている。
【はいちのだらだラジオ】 第61回 - 3万人記念イベントを終えて

【高校数学】 数Ⅰ-100 立体に内接する球
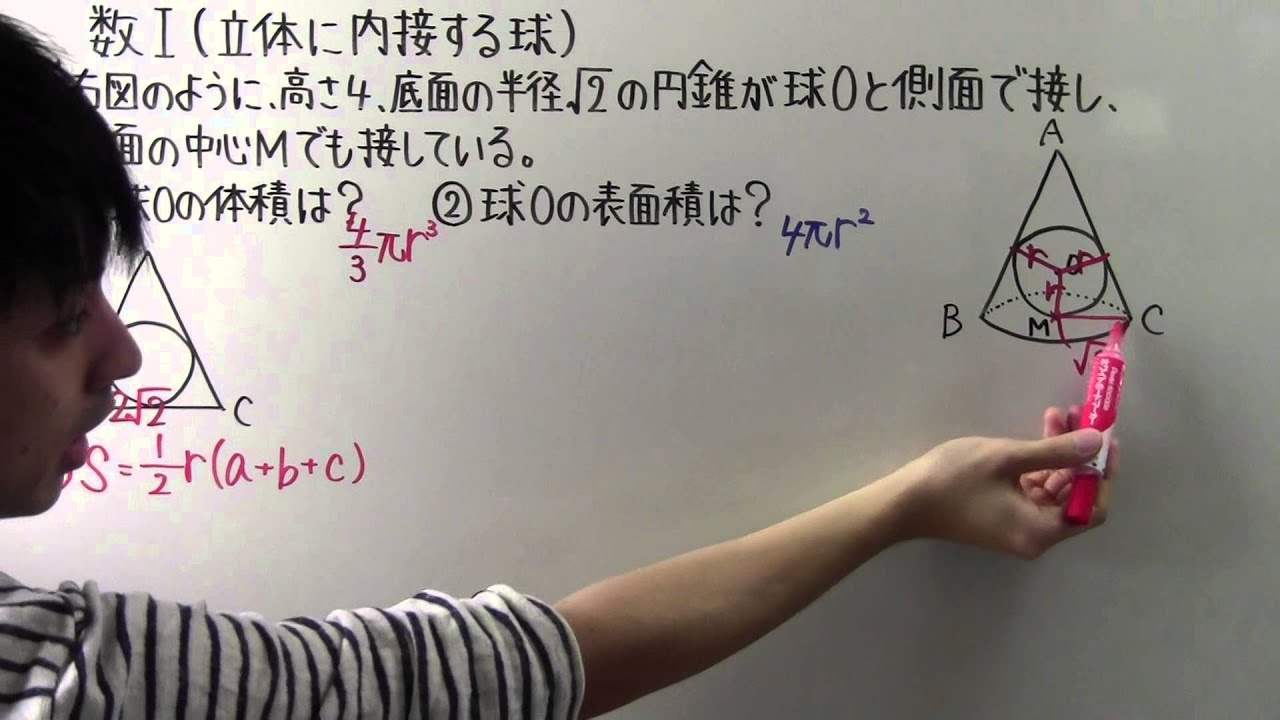
単元:
#数Ⅰ#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎右図のように、高さ4、底面の半径$\sqrt{ 2 }$の円錐球Oと側面で接し、底面の中心Mでも接している。
①球Oの体積は?
②球Oの表面積は?
※図は動画内参照
この動画を見る
◎右図のように、高さ4、底面の半径$\sqrt{ 2 }$の円錐球Oと側面で接し、底面の中心Mでも接している。
①球Oの体積は?
②球Oの表面積は?
※図は動画内参照
【社会】 公民-35 政府の経済活動と租税

単元:
#社会(中学生)#公民
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
政府(国や地方公共団体)が収入を得て、それを支出する経済活動を①____という。
政府の収入は主として税金(租税)によってまかなわれていて、税金は国が集める②____と、地方公共団体が集める③____とに分けられる。
また、所得税や法人税のように、税金を納める義務のある人(納税者)と税金を実際に負担する人(担税者)が一致する税金を④____といい、 酒税や消費税のように一致しない税金を⑤____という。
ちなみに、所得税には、所得が多くなればなるほど税率が高くなる⑥____の方法がとられている。
政府の収入は原則として税金によってまかなわなければならないが、税金だけでは必要な収入を得ることができない場合、政府は税収の不足を補うために⑦____(国の場合は⑧____、地方公共団体の場合は⑨____)を発行して借り入れする。
この動画を見る
政府(国や地方公共団体)が収入を得て、それを支出する経済活動を①____という。
政府の収入は主として税金(租税)によってまかなわれていて、税金は国が集める②____と、地方公共団体が集める③____とに分けられる。
また、所得税や法人税のように、税金を納める義務のある人(納税者)と税金を実際に負担する人(担税者)が一致する税金を④____といい、 酒税や消費税のように一致しない税金を⑤____という。
ちなみに、所得税には、所得が多くなればなるほど税率が高くなる⑥____の方法がとられている。
政府の収入は原則として税金によってまかなわなければならないが、税金だけでは必要な収入を得ることができない場合、政府は税収の不足を補うために⑦____(国の場合は⑧____、地方公共団体の場合は⑨____)を発行して借り入れする。
【高校数学】 数Ⅰ-99 正四面体の切り口

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎1辺の長さが6の正四面体OABCがある。
OAの中点をL、辺OBを2:1に分ける点をM、辺OC上で2ON=NCを満たす点をNとする。
①$LM$の長さは?
②$\cos \angle MLN$の値は?
③$△LMN$の面積は?
この動画を見る
◎1辺の長さが6の正四面体OABCがある。
OAの中点をL、辺OBを2:1に分ける点をM、辺OC上で2ON=NCを満たす点をNとする。
①$LM$の長さは?
②$\cos \angle MLN$の値は?
③$△LMN$の面積は?
【社会】 公民-34 貨幣と金融

単元:
#社会(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
資金が不足している人と余裕がある人との間で行われる資金の貸し借りは①____と呼ばれる。
銀行の場合、資金の借り手は貸し手の銀行に対して、借り入れ額(元金)を返済するだけでなく、②____を支払わなければならない。
そして、銀行は借し出し先から②‗‗‗‗‗‗‗‗‗‗を取り、預金者には②‗‗‗‗‗‗‗‗‗‗を支払う。
世界の国々のほとんどが、③____銀行と呼ばれる特別な働きをする銀行を持っていて、 日本では④____銀行がそれにあたる。
④銀行はその役割から⑤____銀行、 ⑥____銀行、⑦____銀行と呼ばれる。
④銀行の発行する紙幣や財務省の発行する硬貨のことを「貨幣(通貨)」と呼ぶ。
だが、 通貨統計を見ると、紙幣や硬貨(⑧____)は通貨全体の1割以下で、ほとんどが銀行預金などの⑨____である。
ちなみに銀行の資金量を変化させ、銀行の 借し出し量を操作して景気や物価に影響をあたえようとすることを⑩____政策という。
この動画を見る
資金が不足している人と余裕がある人との間で行われる資金の貸し借りは①____と呼ばれる。
銀行の場合、資金の借り手は貸し手の銀行に対して、借り入れ額(元金)を返済するだけでなく、②____を支払わなければならない。
そして、銀行は借し出し先から②‗‗‗‗‗‗‗‗‗‗を取り、預金者には②‗‗‗‗‗‗‗‗‗‗を支払う。
世界の国々のほとんどが、③____銀行と呼ばれる特別な働きをする銀行を持っていて、 日本では④____銀行がそれにあたる。
④銀行はその役割から⑤____銀行、 ⑥____銀行、⑦____銀行と呼ばれる。
④銀行の発行する紙幣や財務省の発行する硬貨のことを「貨幣(通貨)」と呼ぶ。
だが、 通貨統計を見ると、紙幣や硬貨(⑧____)は通貨全体の1割以下で、ほとんどが銀行預金などの⑨____である。
ちなみに銀行の資金量を変化させ、銀行の 借し出し量を操作して景気や物価に影響をあたえようとすることを⑩____政策という。
【高校数学】 数Ⅰ-98 三角形の内角の二等分線

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎$\angle A=60°, AB=4.AC=3$である△ABCの$\angle A$の二等分線が辺BCと交わる点をDとするとき、線分ADの長さを求めよう。
この動画を見る
◎$\angle A=60°, AB=4.AC=3$である△ABCの$\angle A$の二等分線が辺BCと交わる点をDとするとき、線分ADの長さを求めよう。
【社会】 公民-33 市場経済と価格

単元:
#社会(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
商店やデパートなどの商業施設に注目するのではなく、特定の商品に着目して、その商品 が売買される場の全体を①____といい、これが社会のすみずみまで張りめぐらされている経済を②____経済と呼ぶ。
高い商品の価格は、買おうとする量(③____量)と売ろうとする量(④____量)の関係で変化し、③‗‗‗‗‗‗‗‗‗‗量が④‗‗‗‗‗‗‗‗‗‗量を上回ると価格は⑤____する。
ちなみに③‗‗‗‗‗‗‗‗‗‗量と④‗‗‗‗‗‗‗‗‗‗量を一致させる価格を⑥____価格という。
また、少数の大企業が生産や販売市場を支配している⑦____産業では、価格競争が弱まり、企業が足なみをそろえて、価格(⑧____価格)や生産量を決めることが多くなる。
それにより、消費者に不利益を生じる可能性があるため、競争をうながすために⑨____法が制定され、⑩____が運用にあたっている。
※グラフは動画内参照
この動画を見る
商店やデパートなどの商業施設に注目するのではなく、特定の商品に着目して、その商品 が売買される場の全体を①____といい、これが社会のすみずみまで張りめぐらされている経済を②____経済と呼ぶ。
高い商品の価格は、買おうとする量(③____量)と売ろうとする量(④____量)の関係で変化し、③‗‗‗‗‗‗‗‗‗‗量が④‗‗‗‗‗‗‗‗‗‗量を上回ると価格は⑤____する。
ちなみに③‗‗‗‗‗‗‗‗‗‗量と④‗‗‗‗‗‗‗‗‗‗量を一致させる価格を⑥____価格という。
また、少数の大企業が生産や販売市場を支配している⑦____産業では、価格競争が弱まり、企業が足なみをそろえて、価格(⑧____価格)や生産量を決めることが多くなる。
それにより、消費者に不利益を生じる可能性があるため、競争をうながすために⑨____法が制定され、⑩____が運用にあたっている。
※グラフは動画内参照
【高校数学】 数Ⅰ-97 内接円と外接円の半径

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎AB=7,BC=8,CA=5の△ABCについて。
①外接円の半径Rは?
②内接円の半径rは?
この動画を見る
◎AB=7,BC=8,CA=5の△ABCについて。
①外接円の半径Rは?
②内接円の半径rは?
【はいちのだらだラジオ】 第60回 - なんだか感謝を伝えたくて

【社会】 公民-32 企業と労働者

単元:
#社会(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
資本金や従業員数によって、企業は①____と②____に分かれる。
また、グローバル化が進むにつれて、アジアをはじめとする海外の国々に現地籍の企業をつくる③______も増えている。
労働者と企業の関係は必ずしも対等ではないため、労働者は④____を結成し、労働条件の改善を企業側に要求することができる。
また、日本では、 ⑤____法、⑥____法、⑦____法 の3つは労働三法と呼ばれている。
近年では、労働のあり方などもさま変わりしていて、現在の日本の労働者のおよそ3人に1人が、アルバイト、パート、派遣労働者、契約労働者などの⑧____である。
また、グローバル化が進むにつれて⑨____が増えている。
この動画を見る
資本金や従業員数によって、企業は①____と②____に分かれる。
また、グローバル化が進むにつれて、アジアをはじめとする海外の国々に現地籍の企業をつくる③______も増えている。
労働者と企業の関係は必ずしも対等ではないため、労働者は④____を結成し、労働条件の改善を企業側に要求することができる。
また、日本では、 ⑤____法、⑥____法、⑦____法 の3つは労働三法と呼ばれている。
近年では、労働のあり方などもさま変わりしていて、現在の日本の労働者のおよそ3人に1人が、アルバイト、パート、派遣労働者、契約労働者などの⑧____である。
また、グローバル化が進むにつれて⑨____が増えている。
【社会】 公民-31 企業の役割と意義

単元:
#社会(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
現代の経済では、企業が生産の役割を専門的にになっている。
ちなみに、①____ を目的とする民間企業を②____といい、①‗‗‗‗‗‗‗‗‗‗を 目的としない企業を③____という。
①‗‗‗‗‗‗‗‗‗‗を生み出すもととなる資金は④____と呼ばれ、私たちの経済は⑤____経済と呼ばれている。
②‗‗‗‗‗‗‗‗‗‗は、農家や個人商店などの個人企業と、複数の人々が資金を 出し合ってつくった法人企業に大別でき、法人企業の中でも代表的なものが⑥____である。
⑥‗‗‗‗‗‗‗‗‗‗は、⑦____の発行によって得られた資金をもとに設立される企業で、⑦‗‗‗‗‗‗‗‗‗‗を購入した人は⑧____と呼ばれ、⑧‗‗‗‗‗‗‗‗‗‗総会に出席して経営方針や①‗‗‗‗‗‗‗‗‗‗の分配などに関する議決をしたり、①‗‗‗‗‗‗‗‗‗‗の一部を⑨____として受け取ったりする権利を持っている。
企業の発行した⑦‗‗‗‗‗‗‗‗‗‗は⑩______で売買される。
この動画を見る
現代の経済では、企業が生産の役割を専門的にになっている。
ちなみに、①____ を目的とする民間企業を②____といい、①‗‗‗‗‗‗‗‗‗‗を 目的としない企業を③____という。
①‗‗‗‗‗‗‗‗‗‗を生み出すもととなる資金は④____と呼ばれ、私たちの経済は⑤____経済と呼ばれている。
②‗‗‗‗‗‗‗‗‗‗は、農家や個人商店などの個人企業と、複数の人々が資金を 出し合ってつくった法人企業に大別でき、法人企業の中でも代表的なものが⑥____である。
⑥‗‗‗‗‗‗‗‗‗‗は、⑦____の発行によって得られた資金をもとに設立される企業で、⑦‗‗‗‗‗‗‗‗‗‗を購入した人は⑧____と呼ばれ、⑧‗‗‗‗‗‗‗‗‗‗総会に出席して経営方針や①‗‗‗‗‗‗‗‗‗‗の分配などに関する議決をしたり、①‗‗‗‗‗‗‗‗‗‗の一部を⑨____として受け取ったりする権利を持っている。
企業の発行した⑦‗‗‗‗‗‗‗‗‗‗は⑩______で売買される。
【高校数学】 数Ⅰ-96 円に内接する四角形
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
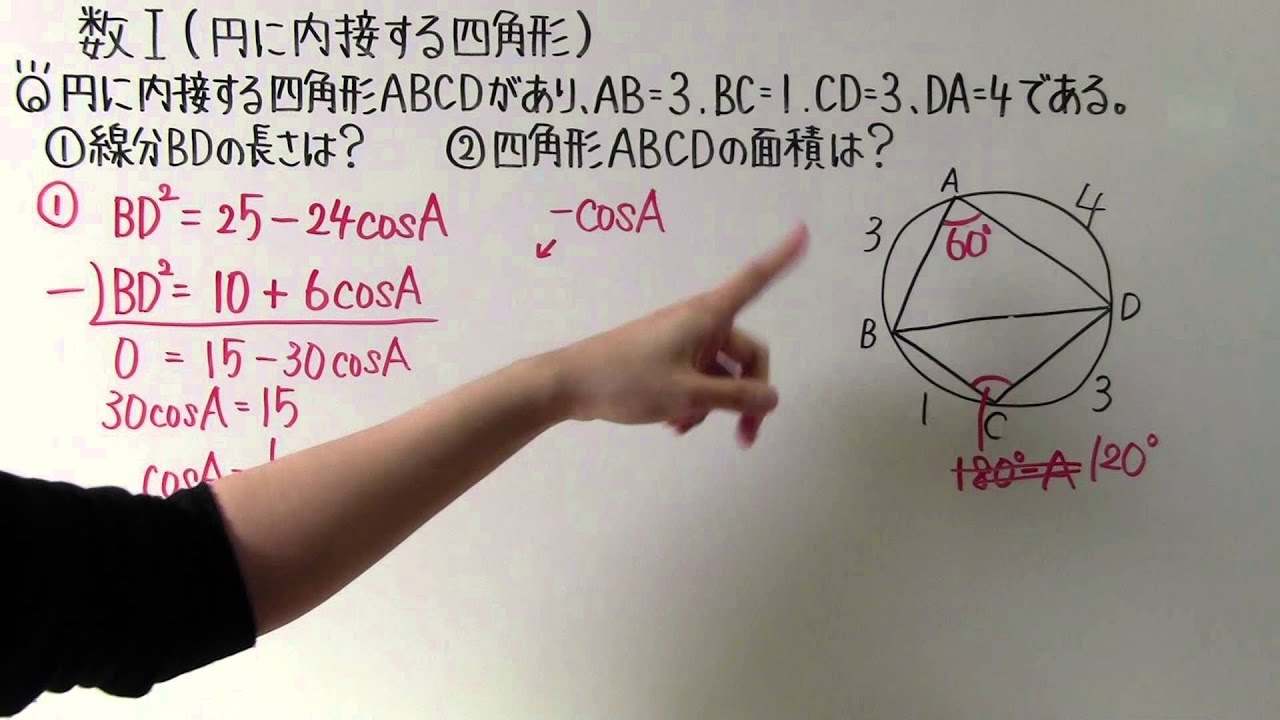
◎円に内接する四角形ABCDがあり、AB=3,BC=1,DA=4である。
①線分BDの長さは?
②四角形ABCDの面積は?
この動画を見る
◎円に内接する四角形ABCDがあり、AB=3,BC=1,DA=4である。
①線分BDの長さは?
②四角形ABCDの面積は?
【社会】 公民-30 消費者の権利

単元:
#社会(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
現代社会では、消費者が自分の意思と判断によって商品を購入すること(①____)は難しくなっており、商品の購入などをめぐる問題(②____問題)も増えている。
そして、問題が深刻化すると、消費者は団体を結成して消費者運動をするようになった。
その根底には、1962年にアメリカの③____大統領がかかげた4つの権利(④____権利、⑤____権利、⑥____ 権利、⑦____権利)がある。
日本でも、欠陥商品によって消費者が被害を受けた際の企業の責任について定めた⑧____法(____法)や、消費者の権利を明確化するとともに、企業と行政の責任を定めた⑨____法などの法律が制定された。
しかし忘れてはいけないのは、消費者は権利とともに責任を負っていること。
なので、消費者自身で商品に関する知識や情報を広く収集して、判断力を備えた⑩____になることを心がけなければならない。
この動画を見る
現代社会では、消費者が自分の意思と判断によって商品を購入すること(①____)は難しくなっており、商品の購入などをめぐる問題(②____問題)も増えている。
そして、問題が深刻化すると、消費者は団体を結成して消費者運動をするようになった。
その根底には、1962年にアメリカの③____大統領がかかげた4つの権利(④____権利、⑤____権利、⑥____ 権利、⑦____権利)がある。
日本でも、欠陥商品によって消費者が被害を受けた際の企業の責任について定めた⑧____法(____法)や、消費者の権利を明確化するとともに、企業と行政の責任を定めた⑨____法などの法律が制定された。
しかし忘れてはいけないのは、消費者は権利とともに責任を負っていること。
なので、消費者自身で商品に関する知識や情報を広く収集して、判断力を備えた⑩____になることを心がけなければならない。
【高校数学】 数Ⅰ-95 多角形の面積
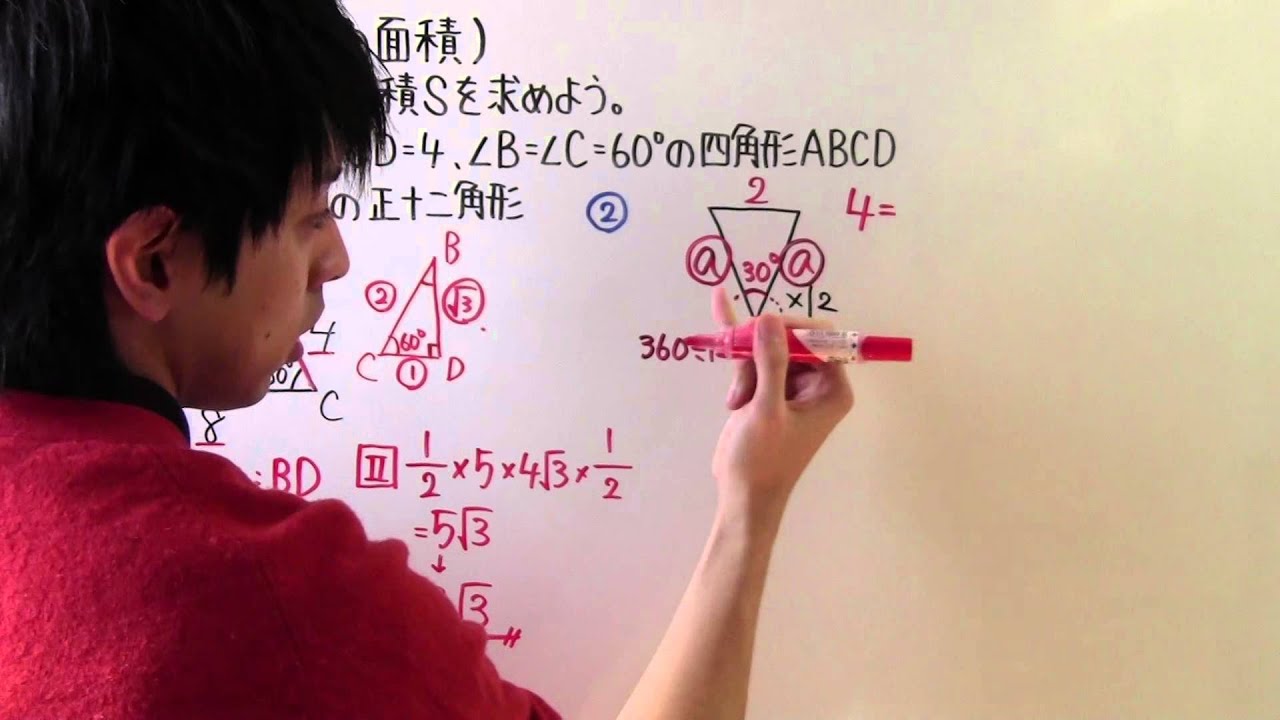
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次のような図形の面積Sを求めよう。
①$AB=5,BC=8,CD=4,\angle B=\angle C=60°$の四角形ABCD
②1辺の長さが2の正十二角形
この動画を見る
◎次のような図形の面積Sを求めよう。
①$AB=5,BC=8,CD=4,\angle B=\angle C=60°$の四角形ABCD
②1辺の長さが2の正十二角形
【社会】 地理-44 日本の人口問題

単元:
#社会(高校生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
日本の大都市は、第二次世界大戦後から高度経済成長期にかけて、 限られた土地に企業や人口が集中する①____地域となった。
その後、大都市はさまざまな問題をかかえていることに加え、地価も高かったため、都心の人口が減少し、郊外の人口が増加した時期もあった(②____現象)。
しかし、1990年代に地価が下がると、再び都心に近い地域の人口が 増加した(③______現象)。
一方、農村では人口の減少と④____化が進んでいるため、地域社会を維持する機能が弱くなっていて、このような地域は⑤____地域と呼ばれており、 その中でも、65歳以上の人口が過半数をしめる集落を⑥____集落と呼ぶ。
なので、そのような地域では、大都市には見られない豊かな自然や景観、伝統的な生活や文化、特産品を活用した⑦______
が行われている。
この動画を見る
日本の大都市は、第二次世界大戦後から高度経済成長期にかけて、 限られた土地に企業や人口が集中する①____地域となった。
その後、大都市はさまざまな問題をかかえていることに加え、地価も高かったため、都心の人口が減少し、郊外の人口が増加した時期もあった(②____現象)。
しかし、1990年代に地価が下がると、再び都心に近い地域の人口が 増加した(③______現象)。
一方、農村では人口の減少と④____化が進んでいるため、地域社会を維持する機能が弱くなっていて、このような地域は⑤____地域と呼ばれており、 その中でも、65歳以上の人口が過半数をしめる集落を⑥____集落と呼ぶ。
なので、そのような地域では、大都市には見られない豊かな自然や景観、伝統的な生活や文化、特産品を活用した⑦______
が行われている。
【社会】 地理-43 日本の人口
単元:
#社会(高校生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
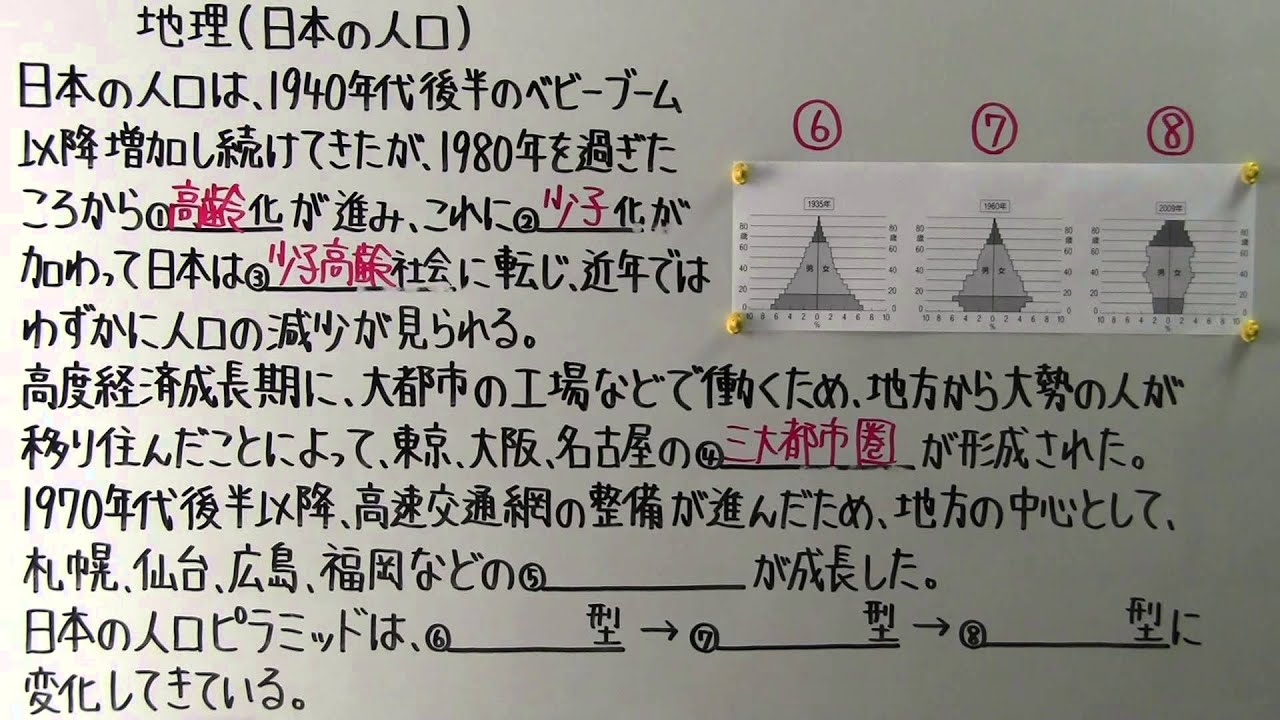
日本の人口は、1940年代後半のベビーブーム以降増加し続けてきたが、1980年を過ぎたころから①____化が進み、これに②____化が加わって日本は③____社会に転じ、近年ではわずかに人口の減少が見られる。
高度経済成長期に、大都市の工場などで働くため、地方から大勢の人が移り住んだことによって、東京、大阪、名古屋の④____が形成された。
1970年代後半以降、高速交通網の整備が進んだため、地方の中心として、 札幌、仙台、広島、福岡などの⑤____が成長した。
日本の人口ピラミッドは、⑥____型→⑦____型→⑧____型に変化してきている。
この動画を見る
日本の人口は、1940年代後半のベビーブーム以降増加し続けてきたが、1980年を過ぎたころから①____化が進み、これに②____化が加わって日本は③____社会に転じ、近年ではわずかに人口の減少が見られる。
高度経済成長期に、大都市の工場などで働くため、地方から大勢の人が移り住んだことによって、東京、大阪、名古屋の④____が形成された。
1970年代後半以降、高速交通網の整備が進んだため、地方の中心として、 札幌、仙台、広島、福岡などの⑤____が成長した。
日本の人口ピラミッドは、⑥____型→⑦____型→⑧____型に変化してきている。
【はいちのだらだラジオ】 第59回 - 相談にこたえるよ①

【高校数学】 数Ⅰ-94 三角形の面積② ・ ヘロンの公式編

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
3辺の長さがa,b,cである△ABCの面積Sは、
S=①____________(t=②____________)
◎次のような△ABCの面積を求めよう。
③a=8,b=6,C=4
④a=7,b=5,C=9
この動画を見る
3辺の長さがa,b,cである△ABCの面積Sは、
S=①____________(t=②____________)
◎次のような△ABCの面積を求めよう。
③a=8,b=6,C=4
④a=7,b=5,C=9
【社会】 地理-42 世界の人口
単元:
#社会(中学生)#社会(高校生)#地理#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
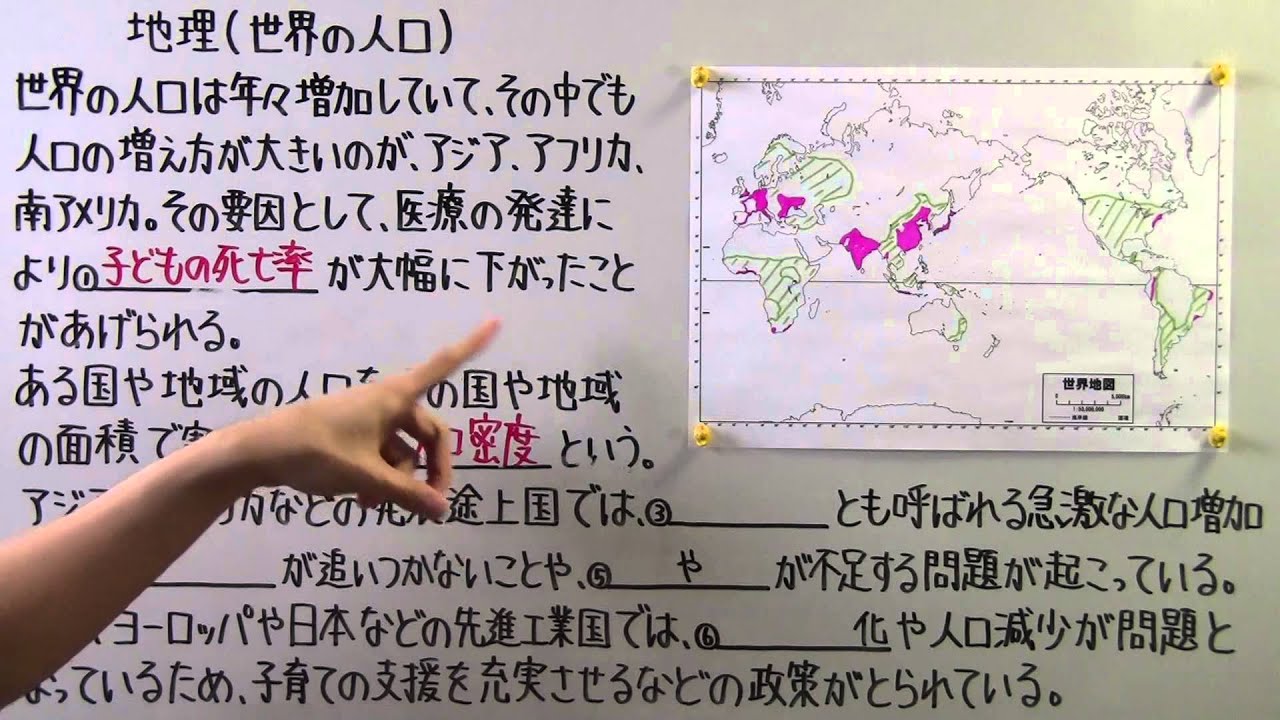
世界の人口は年々増加していて、その中でも人口の増え方が大きいのが、アジア、アフリカ、南アメリカ。
その要因として、医療の発達により①________が大幅にあげられる。
ある国や地域の人口を、その国の値域の面積で割ったものを②________という。
アジアやアフリカなどの発展途上国では、③____と呼ばれる急激な人口増加によって④____が追いつかないことや、⑤____や____が不足する問題が起こっている。
一方、ヨーロッパや日本などの先進国では、⑥____化や人口減少が問題となっているため、子育てを充実させるなどの政策がとられている。
この動画を見る
世界の人口は年々増加していて、その中でも人口の増え方が大きいのが、アジア、アフリカ、南アメリカ。
その要因として、医療の発達により①________が大幅にあげられる。
ある国や地域の人口を、その国の値域の面積で割ったものを②________という。
アジアやアフリカなどの発展途上国では、③____と呼ばれる急激な人口増加によって④____が追いつかないことや、⑤____や____が不足する問題が起こっている。
一方、ヨーロッパや日本などの先進国では、⑥____化や人口減少が問題となっているため、子育てを充実させるなどの政策がとられている。
【はいちのだらだラジオ】 第58回 - きなこについて

【高校数学】 数Ⅰ-93 三角形の面積① ・ 基本編

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
三角形の面積S=①__________________
△ABCの内接円の半径rとするとS=②____________
※図は動画内参照
◎次の△ABCの面積Sを求めよう。
③$b=3,C=2,A=120°$
④$a=2\sqrt{ 2 },b=3,A110°,B=25°$
⑤$a=6,b=3,c=7$
この動画を見る
三角形の面積S=①__________________
△ABCの内接円の半径rとするとS=②____________
※図は動画内参照
◎次の△ABCの面積Sを求めよう。
③$b=3,C=2,A=120°$
④$a=2\sqrt{ 2 },b=3,A110°,B=25°$
⑤$a=6,b=3,c=7$
【高校数学】 数Ⅰ-92 三角形となる条件

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎3辺の長さが、5,3,xである三角形が鈍角三角形となるように、xの範囲を定めよう。
この動画を見る
◎3辺の長さが、5,3,xである三角形が鈍角三角形となるように、xの範囲を定めよう。
【社会】 地理-45 世界の資源とエネルギー

単元:
#社会(高校生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎穀物名と鉱山資源名を書こう。
①____________
②____________
③____________
④____________
⑤____________
⑥____________
※地図は動画内参照
世界のエネルギー消費は、年々増加しているため、⑦____化が問題視されている。
その対策として、太陽光や風力などの⑧____エネルギーを利用するなどといった二酸化炭素の排出量削減に向けたさまざまな取り組みがなされている。
また、鉱山資源の埋蔵量には限りがあるため、⑨____社会を実現するために鉱山資源を有効活用する取り組みや、とうもろこしなどを利用した⑩____をエネルギー源とする取り組みなども広がっている。
この動画を見る
◎穀物名と鉱山資源名を書こう。
①____________
②____________
③____________
④____________
⑤____________
⑥____________
※地図は動画内参照
世界のエネルギー消費は、年々増加しているため、⑦____化が問題視されている。
その対策として、太陽光や風力などの⑧____エネルギーを利用するなどといった二酸化炭素の排出量削減に向けたさまざまな取り組みがなされている。
また、鉱山資源の埋蔵量には限りがあるため、⑨____社会を実現するために鉱山資源を有効活用する取り組みや、とうもろこしなどを利用した⑩____をエネルギー源とする取り組みなども広がっている。


