 とある男が授業をしてみた
とある男が授業をしてみた
 とある男が授業をしてみた
とある男が授業をしてみた
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【はいちのだらだラジオ】 第39回-生徒に言い続けた魔法の言葉

単元:
#その他#はいちのだらだラジオ#はいちのだらだラジオ2
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
【はいちのだらだラジオ】
第39回-生徒に言い続けた魔法の言葉
この動画を見る
【はいちのだらだラジオ】
第39回-生徒に言い続けた魔法の言葉
【高校数学】数Ⅰ-37 2次関数③(軸と頂点編)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の2次関数の軸と頂点を求めよう。
①$y=3(x--1)^2-4$
②$y=2x^2+7$
この動画を見る
◎次の2次関数の軸と頂点を求めよう。
①$y=3(x--1)^2-4$
②$y=2x^2+7$
【高校数学】数Ⅰ-36 2次関数②(値域編)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の関数の値域を求めよう。また、最大値、最小値があれば、それをもとめよう。
①$y=2x+1(2 \leqq x \leqq 3)$
②$y=-3x+2(-1 \leqq x \leqq 2)$
③$y=x^2(-3 \leqq x \leqq 1)$
④$y=3x-5(1 \leqq x \lt 4)$
この動画を見る
◎次の関数の値域を求めよう。また、最大値、最小値があれば、それをもとめよう。
①$y=2x+1(2 \leqq x \leqq 3)$
②$y=-3x+2(-1 \leqq x \leqq 2)$
③$y=x^2(-3 \leqq x \leqq 1)$
④$y=3x-5(1 \leqq x \lt 4)$
【高校数学】数Ⅰ-35 2次関数①

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎$f_{(x)}=-2x+3$について、次の値を求めよう。
①$f_{(4)}$
②$f_{(0)}$
③$f_{(1-a)}$
◎次の関数グラフが通る象限を書こう。
④$y=2x-5$
⑤$y=4$
この動画を見る
◎$f_{(x)}=-2x+3$について、次の値を求めよう。
①$f_{(4)}$
②$f_{(0)}$
③$f_{(1-a)}$
◎次の関数グラフが通る象限を書こう。
④$y=2x-5$
⑤$y=4$
【社会】 地理-8 様々な地域に住む人々③

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
アフリカ北部の広大な①____さばくの南に接して、
わずかに木や草が生えた土地(②____ )がある。
この地域には、羊ややぎの③____を行ったりしてきたトゥアレグ族などの、さまざまな④____が暮らしている。
①‗‗‗‗‗‗‗さばくや②‗‗‗‗‗‗‗のような地域を⑤____帯といい、一年中暑く、強い日差しがある。
また、①‗‗‗‗‗‗‗さばくでは、地下水がわき出る⑥____以外では樹木はほとんど育たないがわずかに木が生えた草原を焼きはらって畑をつくり、焼いてできた灰を肥料として活用する⑦____が行われてきた。
その後、⑧____設備の整備などにより、 主食がとうもろこしや米に変わっていった。
しかし、土地を休ませずに耕作を続けるために、草も育たない土地になってしまうこと(⑨____化)が問題視されている。
この動画を見る
アフリカ北部の広大な①____さばくの南に接して、
わずかに木や草が生えた土地(②____ )がある。
この地域には、羊ややぎの③____を行ったりしてきたトゥアレグ族などの、さまざまな④____が暮らしている。
①‗‗‗‗‗‗‗さばくや②‗‗‗‗‗‗‗のような地域を⑤____帯といい、一年中暑く、強い日差しがある。
また、①‗‗‗‗‗‗‗さばくでは、地下水がわき出る⑥____以外では樹木はほとんど育たないがわずかに木が生えた草原を焼きはらって畑をつくり、焼いてできた灰を肥料として活用する⑦____が行われてきた。
その後、⑧____設備の整備などにより、 主食がとうもろこしや米に変わっていった。
しかし、土地を休ませずに耕作を続けるために、草も育たない土地になってしまうこと(⑨____化)が問題視されている。
【高校数学】数Ⅰ-34 命題⑧
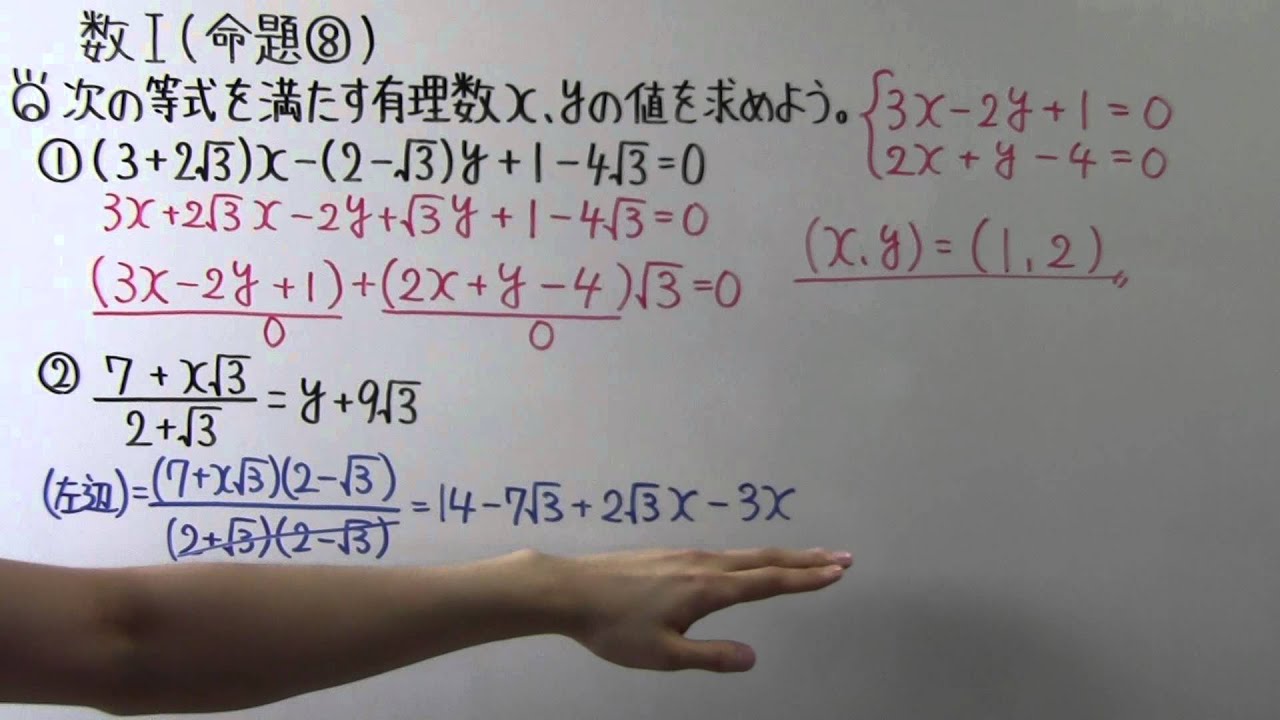
単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の等式を満たす有理数x,yの値を求めよう。
①$(3+2\sqrt{ 3 })x-(2-\sqrt{ 3 })y+1-4\sqrt{ 3 }=0$
②$\displaystyle \frac{7+x\sqrt{ 3 }}{2+\sqrt{ 3 }}=y+9\sqrt{ 3 }$
この動画を見る
◎次の等式を満たす有理数x,yの値を求めよう。
①$(3+2\sqrt{ 3 })x-(2-\sqrt{ 3 })y+1-4\sqrt{ 3 }=0$
②$\displaystyle \frac{7+x\sqrt{ 3 }}{2+\sqrt{ 3 }}=y+9\sqrt{ 3 }$
【社会】 地理-7 様々な地域に住む人々②
単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
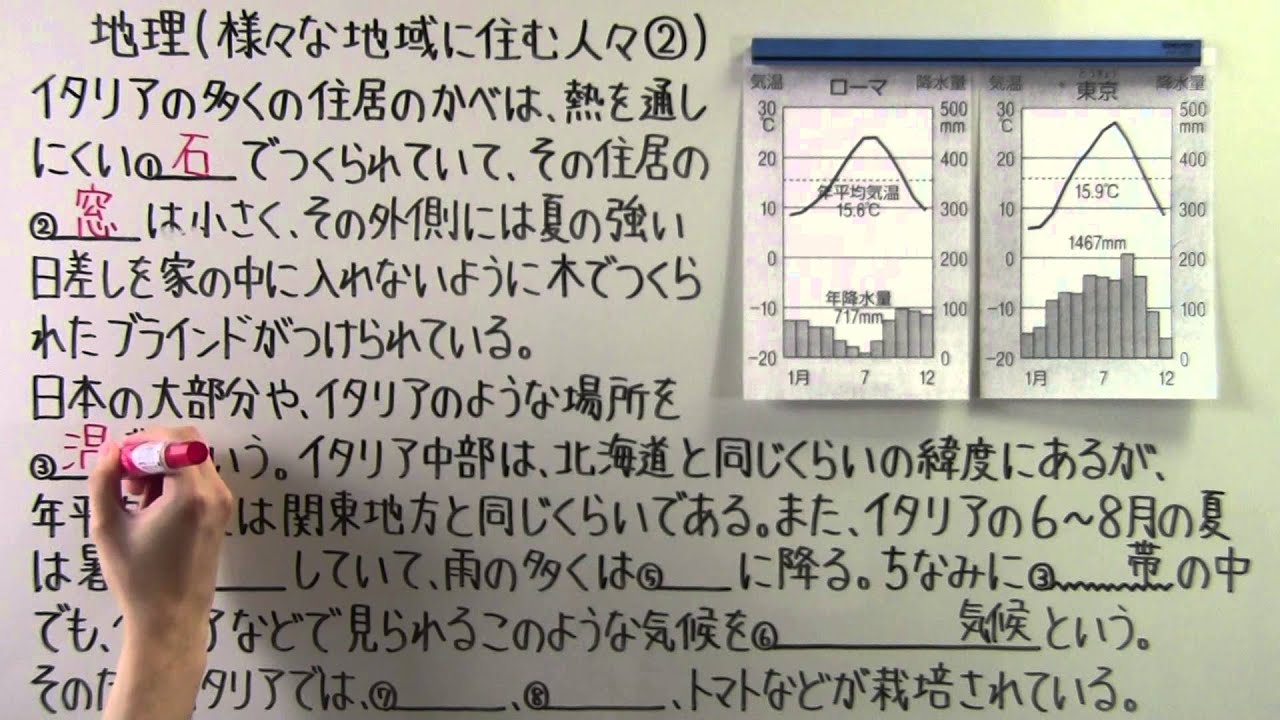
イタリアの多くの住居のかべは、熱を通しにくい①____でつくられていて、その住居の②____は小さく、その外側には夏の強い日差しを家の中に入れないように木でつくられたブラインドがつけられている。
日本の大部分や、イタリアのような場所を③____帯という。
イタリア中部は、北海道と同じくらいの緯度にあるが、 年平均気温は関東地方と同じくらいである。
また、イタリアの6~8月の夏は暑く、④____していて、雨の多くは⑤____に降る。
ちなみに③‗‗‗‗‗‗の中でも、イタリアなどで見られるこのような気候を⑥________ 気候という。
そのため、イタリアでは、⑦____、⑧____、トマトなどが栽培されている。
この動画を見る
イタリアの多くの住居のかべは、熱を通しにくい①____でつくられていて、その住居の②____は小さく、その外側には夏の強い日差しを家の中に入れないように木でつくられたブラインドがつけられている。
日本の大部分や、イタリアのような場所を③____帯という。
イタリア中部は、北海道と同じくらいの緯度にあるが、 年平均気温は関東地方と同じくらいである。
また、イタリアの6~8月の夏は暑く、④____していて、雨の多くは⑤____に降る。
ちなみに③‗‗‗‗‗‗の中でも、イタリアなどで見られるこのような気候を⑥________ 気候という。
そのため、イタリアでは、⑦____、⑧____、トマトなどが栽培されている。
【はいちのだらだラジオ】 第38回-忘れない勉強法?

【高校数学】数Ⅰ-33 命題⑦(続 背理法編)

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎命題「nは整数とする。$n^2$が3倍ならば、nは3倍数である」は真である。
これを利用して、$\sqrt{ 3 }$が無理であることを証明しよう。
この動画を見る
◎命題「nは整数とする。$n^2$が3倍ならば、nは3倍数である」は真である。
これを利用して、$\sqrt{ 3 }$が無理であることを証明しよう。
【社会】 地理-6 様々な地域に住む人々①

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
北極海に面したカナダ北部には①____と呼ばれる人々が生活していて、かつては冬になると海の氷の上に雪を固めて積み上げた ドーム型の②____に住み、あざらしを追っていた。
この地域のように、気温0℃以下の期間が長く、一年の大半が雪と氷におおわれている場所を③____帯という。
一方、シベリアでは冬に-30℃を下回る日がしばしばあるが、夏には30℃近く になる日もある。
このように、一年の気温差が大きい地域を④____帯という。
また、シベリアでは、寒さに強いまつ、もみ、しらかばが育ち、これらの広大な針葉樹の森林を⑤____ という。
※グラフは動画内参照
この動画を見る
北極海に面したカナダ北部には①____と呼ばれる人々が生活していて、かつては冬になると海の氷の上に雪を固めて積み上げた ドーム型の②____に住み、あざらしを追っていた。
この地域のように、気温0℃以下の期間が長く、一年の大半が雪と氷におおわれている場所を③____帯という。
一方、シベリアでは冬に-30℃を下回る日がしばしばあるが、夏には30℃近く になる日もある。
このように、一年の気温差が大きい地域を④____帯という。
また、シベリアでは、寒さに強いまつ、もみ、しらかばが育ち、これらの広大な針葉樹の森林を⑤____ という。
※グラフは動画内参照
【社会】 地理-5 国境の決まり方

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
国と国の境界のことを国境という。
そして、国境線にはおもに2つの 決め方がある。
$\boxed{1}$①____、②____、湖、海などの自然物を利用した国境線(③____国境)
$\boxed{2}$④____、⑤____などを利用した人工的な国境線(⑥____国境)
アフリカ州に、まっすぐな国境線が多いのは、かつてこの地を⑦____としたヨーロッパの国々が引いた境界線を、今も国境線として使っているからである。
また、国境は海上にある場合もある。そして、日本やニュージーランドのような 国々を⑧____といい、一方、国土がまったく海に面していない国々を⑨____という。
この動画を見る
国と国の境界のことを国境という。
そして、国境線にはおもに2つの 決め方がある。
$\boxed{1}$①____、②____、湖、海などの自然物を利用した国境線(③____国境)
$\boxed{2}$④____、⑤____などを利用した人工的な国境線(⑥____国境)
アフリカ州に、まっすぐな国境線が多いのは、かつてこの地を⑦____としたヨーロッパの国々が引いた境界線を、今も国境線として使っているからである。
また、国境は海上にある場合もある。そして、日本やニュージーランドのような 国々を⑧____といい、一方、国土がまったく海に面していない国々を⑨____という。
【はいちのだらだラジオ】 第37回-報告と今年の夏について

【高校数学】数Ⅰ-32 命題⑥(背理法編)

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎$\sqrt{ 2 }$が無理数であることを用いて、$5-\sqrt{ 2 }$が無理数であることを証明しよう。
この動画を見る
◎$\sqrt{ 2 }$が無理数であることを用いて、$5-\sqrt{ 2 }$が無理数であることを証明しよう。
【社会】 地理-4 世界の国々と地域区分
単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
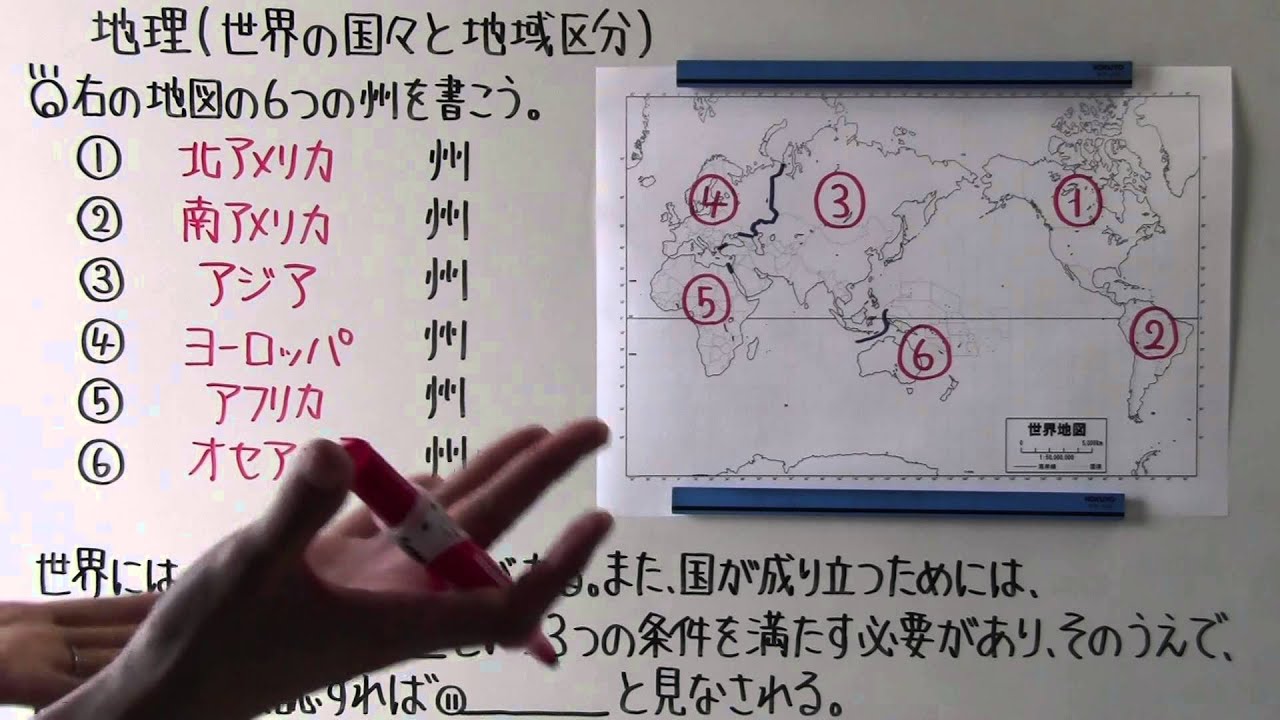
◎右の地図の6つの州を書こう。
①___________州
②___________州
③___________州
④___________州
⑤___________州
⑥___________州
世界には⑦____あまりの国がある。
国が成り立つためには、⑧____、⑨____、⑩____という3つの条件を満たす必要があり、その上ほかの国が承認すれば⑪____と見なされる。
※図は動画内参照
この動画を見る
◎右の地図の6つの州を書こう。
①___________州
②___________州
③___________州
④___________州
⑤___________州
⑥___________州
世界には⑦____あまりの国がある。
国が成り立つためには、⑧____、⑨____、⑩____という3つの条件を満たす必要があり、その上ほかの国が承認すれば⑪____と見なされる。
※図は動画内参照
【高校数学】数Ⅰ-31 命題⑤

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎x,yは実数とする。
次の命題の逆、裏、対偶を書き、それぞれ真偽を調べよう。
①$x=-1$ならば$x^2=1$
[逆]
[裏]
[対偶]
②$x+y>2$ならば$x>0$または$y>2$
[逆]
[裏]
[対偶]
この動画を見る
◎x,yは実数とする。
次の命題の逆、裏、対偶を書き、それぞれ真偽を調べよう。
①$x=-1$ならば$x^2=1$
[逆]
[裏]
[対偶]
②$x+y>2$ならば$x>0$または$y>2$
[逆]
[裏]
[対偶]
【社会】 地理-3 地球上の位置をあらわそう

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
地球儀などにひかれている縦の線を①____(②____をあらわしている)といい横の線を③____(④____をあらわしている)という。
②‗‗‗‗‗‗は、イギリスの⑤____を通る⑥____線を0度として、それより東を⑦____、それより西を⑧____と呼ぶ。
④‗‗‗‗‗‗は⑨____を0度として、それより北を⑩____、それより南を⑪____と呼び、⑨‗‗‗‗‗‗付近では年じゅう気温が⑫____。
ちなみに④‗‗‗‗‗‗の高い地域 では、夏に太陽が沈まない時期(⑬____)がある。
※図は動画内参照
この動画を見る
地球儀などにひかれている縦の線を①____(②____をあらわしている)といい横の線を③____(④____をあらわしている)という。
②‗‗‗‗‗‗は、イギリスの⑤____を通る⑥____線を0度として、それより東を⑦____、それより西を⑧____と呼ぶ。
④‗‗‗‗‗‗は⑨____を0度として、それより北を⑩____、それより南を⑪____と呼び、⑨‗‗‗‗‗‗付近では年じゅう気温が⑫____。
ちなみに④‗‗‗‗‗‗の高い地域 では、夏に太陽が沈まない時期(⑬____)がある。
※図は動画内参照
【高校数学】数Ⅰ-30 命題④

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎x,yは実数、m,nは自然数とする。
次の条件の否定を書こう。
①$x<-1$かつ$y \geqq 2$
②$-5 \leqq x<3$
③nは奇数または3の倍数
④m,nともに6の倍数
◎次の命題の否定を書き、その真偽を調べよう。
⑤すべての素数nについて、nは奇数である。
この動画を見る
◎x,yは実数、m,nは自然数とする。
次の条件の否定を書こう。
①$x<-1$かつ$y \geqq 2$
②$-5 \leqq x<3$
③nは奇数または3の倍数
④m,nともに6の倍数
◎次の命題の否定を書き、その真偽を調べよう。
⑤すべての素数nについて、nは奇数である。
【はいちのだらだラジオ】 第36回-学校やクラスになじめない

単元:
#その他#はいちのだらだラジオ#はいちのだらだラジオ2
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
【はいちのだらだラジオ】
第36回-学校やクラスになじめない
この動画を見る
【はいちのだらだラジオ】
第36回-学校やクラスになじめない
【高校数学】数Ⅰ-29 命題③

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎x,yは実数とする。
次の▭にあてはまるものを、下のⒶ~Ⓓから選ぼう。
Ⓐ必要十分条件である
Ⓑ必要条件ではあるが、十分条件ではない
Ⓒ十分条件ではあるが、必要条件ではない
Ⓓ必要条件でも十分条件でもない
①$xy=0$は、$x^2+y^2>0$が成立するための▭
②$△ABC∞△PQR$は、$△ABC \equiv △PQR$であるための▭
③$|x|<1$かつ$|y|<1$は、$x^2+y^2<1$であるための▭
この動画を見る
◎x,yは実数とする。
次の▭にあてはまるものを、下のⒶ~Ⓓから選ぼう。
Ⓐ必要十分条件である
Ⓑ必要条件ではあるが、十分条件ではない
Ⓒ十分条件ではあるが、必要条件ではない
Ⓓ必要条件でも十分条件でもない
①$xy=0$は、$x^2+y^2>0$が成立するための▭
②$△ABC∞△PQR$は、$△ABC \equiv △PQR$であるための▭
③$|x|<1$かつ$|y|<1$は、$x^2+y^2<1$であるための▭
【社会】 地理-2 世界地図

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
地球を縮めたものを①____という。
しかし、これだと世界全体を一度に見ることができないためいろいろな世界地図がつくられた。
◎それぞれの世界地図の特徴を覚えよう。
モルワイデ図法…②____が正しい地図
正距方位図法…③____からの④____と⑤____が正しい地図
メルカトル図法…経線と緯線が直角に交わっていて、赤道から離れるほど、実際よりも面積が⑥____地図
※図は動画内参照
この動画を見る
地球を縮めたものを①____という。
しかし、これだと世界全体を一度に見ることができないためいろいろな世界地図がつくられた。
◎それぞれの世界地図の特徴を覚えよう。
モルワイデ図法…②____が正しい地図
正距方位図法…③____からの④____と⑤____が正しい地図
メルカトル図法…経線と緯線が直角に交わっていて、赤道から離れるほど、実際よりも面積が⑥____地図
※図は動画内参照
【社会】 地理-1 六大陸と三大洋

単元:
#社会(中学生)#地理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎右下の地図内の六大陸(①~⑥)と三太平洋(⑦~⑨)を書こう。
①___________大陸
②___________大陸
③___________大陸
④___________大陸
⑤___________大陸
⑥___________大陸
⑦___________
⑧___________
⑨___________
ちなみに、地球のおよそ⑩____割は海洋で、陸地は⑪____割。
※地図は動画内参照
この動画を見る
◎右下の地図内の六大陸(①~⑥)と三太平洋(⑦~⑨)を書こう。
①___________大陸
②___________大陸
③___________大陸
④___________大陸
⑤___________大陸
⑥___________大陸
⑦___________
⑧___________
⑨___________
ちなみに、地球のおよそ⑩____割は海洋で、陸地は⑪____割。
※地図は動画内参照
【社会】 歴史-90 日本の変化とこれからの課題

単元:
#社会(中学生)#歴史
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
自民党を与党、社会党を野党第一党とする55年体制①____を首相とする非自民連立内閣が成立したことで終わりをむかえ、その後も日本の政治は 変化を続けている。
また、1980年代末、株式と土地の価格が異常に高くなる不建全な好景気(②______)が発生したが、1991年に崩壊した。
そして、日本の課題の1つとしてあげられるのが、人権の尊重で、③____差別、④____差別、⑤________人や外国人労働者への差別をなくしていかなければならない。
また、日本は⑥____社会なので、安心して 生活できる社会保障制度を築き上げる必要がある。
現在、世界の一体化(⑦________化)が進んでいて、国境をこえる経済活動がさかんになった。
そして、それと同時に、海面の上昇などを引き起こす⑧____
化などの問題は各国が協力していかなければならない。
そして、私たちは、「⑨____ 社会」を築くうえで、地球に生きる人間としての意識を持つことが求められている。
この動画を見る
自民党を与党、社会党を野党第一党とする55年体制①____を首相とする非自民連立内閣が成立したことで終わりをむかえ、その後も日本の政治は 変化を続けている。
また、1980年代末、株式と土地の価格が異常に高くなる不建全な好景気(②______)が発生したが、1991年に崩壊した。
そして、日本の課題の1つとしてあげられるのが、人権の尊重で、③____差別、④____差別、⑤________人や外国人労働者への差別をなくしていかなければならない。
また、日本は⑥____社会なので、安心して 生活できる社会保障制度を築き上げる必要がある。
現在、世界の一体化(⑦________化)が進んでいて、国境をこえる経済活動がさかんになった。
そして、それと同時に、海面の上昇などを引き起こす⑧____
化などの問題は各国が協力していかなければならない。
そして、私たちは、「⑨____ 社会」を築くうえで、地球に生きる人間としての意識を持つことが求められている。
【社会】 歴史-89 冷戦の終結

単元:
#社会(中学生)#歴史
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1985年、ソ連の最高指導者となった①____は、翌年から②____ を行い、民主化をすすめた。
そして、1989年、アメリカのブッシュ大統領との③____会談で、 冷戦の終結を宣言した。
その後、1990年には④東西____が統一し、1991年にはソ連が解体され、ロシア連邦などが独立した。
冷戦後、国連は国際機関としての役割が高まり、1975年に始まった⑤________も重要な役割を果たしている。
また、ヨーロッパでは、1993年にヨーロッパ共同体(EC)が⑥____に発展し、共通通貨として⑦____が使われている。
一方で、民族、宗教、文化のちがいや国家間の対立などから、各地で⑧____が起きている。
これらを解決するうえで、国連の⑨________ の役割は
大きく、民間の非政府組織(NGO)も活躍している。
NGOの中には、紛争や災害で傷ついた人々に対して緊急医療援助活動を行う⑩________などがある。
この動画を見る
1985年、ソ連の最高指導者となった①____は、翌年から②____ を行い、民主化をすすめた。
そして、1989年、アメリカのブッシュ大統領との③____会談で、 冷戦の終結を宣言した。
その後、1990年には④東西____が統一し、1991年にはソ連が解体され、ロシア連邦などが独立した。
冷戦後、国連は国際機関としての役割が高まり、1975年に始まった⑤________も重要な役割を果たしている。
また、ヨーロッパでは、1993年にヨーロッパ共同体(EC)が⑥____に発展し、共通通貨として⑦____が使われている。
一方で、民族、宗教、文化のちがいや国家間の対立などから、各地で⑧____が起きている。
これらを解決するうえで、国連の⑨________ の役割は
大きく、民間の非政府組織(NGO)も活躍している。
NGOの中には、紛争や災害で傷ついた人々に対して緊急医療援助活動を行う⑩________などがある。
【はいちのだらだラジオ】 第35回-質問と言い訳と相談

【高校数学】数Ⅰ-28 命題②

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎x,yは実数とする。
次の▭にあてはまるものを、下のⒶ~Ⓓから選ぼう。
Ⓐ必要十分条件である
Ⓑ必要条件ではあるが、十分条件ではない
Ⓒ十分条件ではあるが、必要条件ではない
Ⓓ必要条件でも十分条件でもない
①$x=2$は、$x^2-x-2=0$であるための▭
②$xy=0$は、$x=0$であるための▭
③$|x|=0$は、$x=0$であるための▭
④$xy>1$は、$x>1$であるための▭
この動画を見る
◎x,yは実数とする。
次の▭にあてはまるものを、下のⒶ~Ⓓから選ぼう。
Ⓐ必要十分条件である
Ⓑ必要条件ではあるが、十分条件ではない
Ⓒ十分条件ではあるが、必要条件ではない
Ⓓ必要条件でも十分条件でもない
①$x=2$は、$x^2-x-2=0$であるための▭
②$xy=0$は、$x=0$であるための▭
③$|x|=0$は、$x=0$であるための▭
④$xy>1$は、$x>1$であるための▭
【高校数学】数Ⅰ-27 命題①

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎a,b,cは実数、dは自然数とする。
次の命題の真偽を調べ、偽のときは判例を1つ示そう。
①$a=0$ならば$ab=0$
②$a^2=b^2$ならば$a=b$
③$a<2$ならば$|a|<4$
④dは2倍の倍数 ならば dの4の倍数
⑤$|a|<3$ならば$a<3$
⑥dは18の約数ならばdは36の約数
この動画を見る
◎a,b,cは実数、dは自然数とする。
次の命題の真偽を調べ、偽のときは判例を1つ示そう。
①$a=0$ならば$ab=0$
②$a^2=b^2$ならば$a=b$
③$a<2$ならば$|a|<4$
④dは2倍の倍数 ならば dの4の倍数
⑤$|a|<3$ならば$a<3$
⑥dは18の約数ならばdは36の約数
【高校数学】数Ⅰ-26 集合③
単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
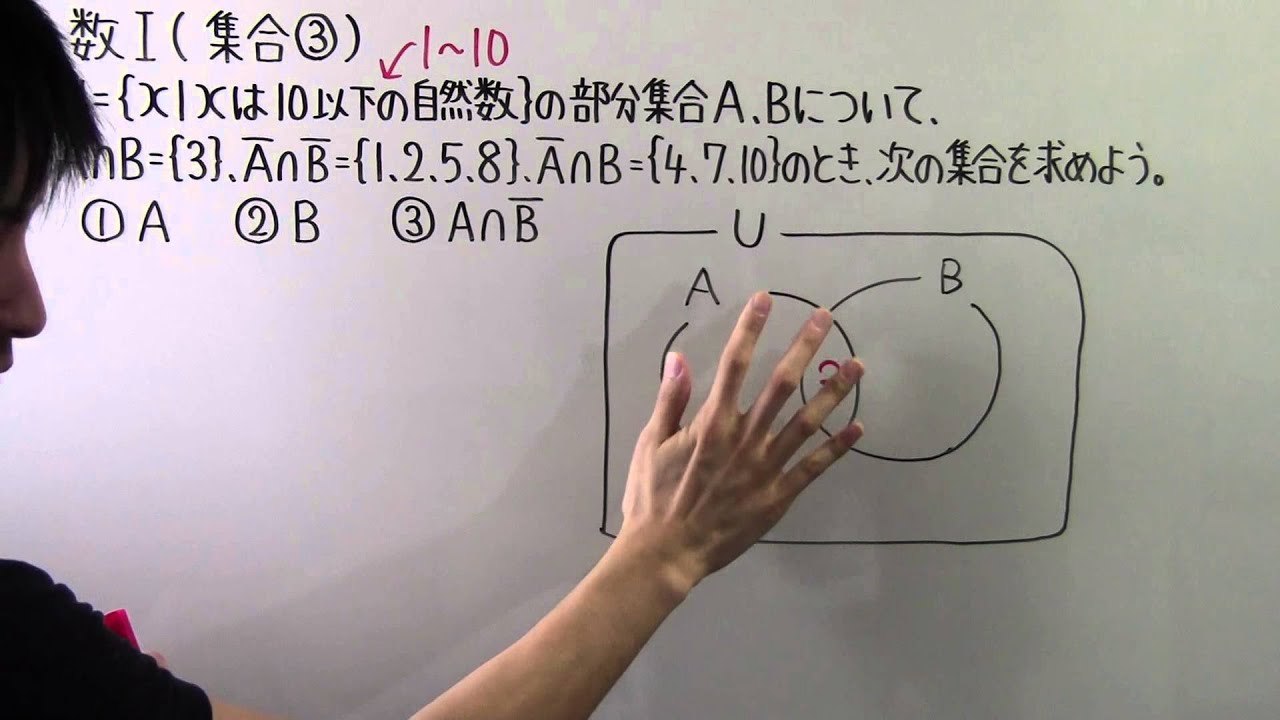
◎U={$x | x$は10以下の自然数}を全体集合とする。
$A \cap B={3}、\overline{ A } \cap \overline{ B }={1,2,5,8,}、\overline{ A } \cap B={4,7,10}$
のとき、次の集合を求めよう。
①$A$
②$B$
③$A \cap\overline{ B}$
この動画を見る
◎U={$x | x$は10以下の自然数}を全体集合とする。
$A \cap B={3}、\overline{ A } \cap \overline{ B }={1,2,5,8,}、\overline{ A } \cap B={4,7,10}$
のとき、次の集合を求めよう。
①$A$
②$B$
③$A \cap\overline{ B}$
【高校数学】数Ⅰ-25 集合②

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎U={$x | x$は9以下の自然数}を全体集合とする。
$U$の部分集合$A={1.3.4.8},B={3.4.5.7.9}$,$C={2,3,7,9}$について、次の集合を求めよう。
①$A \cap B \cap C$
②$A \cap B \cap \overline{ C }$
③$\overline{ A } \cap B \cap C$
④$ \overline{ A \cup B \cup C} $
⑤$\overline{ A } \cap B \cap C$
⑥$(A \cup C) \cap \overline{ B} $
この動画を見る
◎U={$x | x$は9以下の自然数}を全体集合とする。
$U$の部分集合$A={1.3.4.8},B={3.4.5.7.9}$,$C={2,3,7,9}$について、次の集合を求めよう。
①$A \cap B \cap C$
②$A \cap B \cap \overline{ C }$
③$\overline{ A } \cap B \cap C$
④$ \overline{ A \cup B \cup C} $
⑤$\overline{ A } \cap B \cap C$
⑥$(A \cup C) \cap \overline{ B} $
【社会】 歴史-88 日本の経済成長

単元:
#社会(中学生)#歴史
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1950年代半ばまでに戦前の水準をほぼ回復した日本経済は、1955年から73年までの間、年平均で10%程度の成長を続けた (①________)。
それによって、国民の所得は増え、くらしが便利になり1950年代後半には三種の神器(②____、③____、④____)が、1960年代後半には3C(⑤____、⑥____、⑦____)が普及した。
しかし、その一方でさまざまな社会問題も発生し、農村では⑧____化が進み、逆に過密になった都市では住宅不足などが起こった。
また、大気汚染や水質汚濁などの⑨____ も深刻化した。
被害を受けた住民は、四大公害裁判(⑩____、⑪____、⑫____、⑬____)で、 公害を発生させた企業に勝訴した。
その後、1967年に⑭____法が制定され、1971年には⑮____が設置された。
1973年の⑯________によって、①‗‗‗‗‗‗‗‗‗‗は終わりを告げた。
この動画を見る
1950年代半ばまでに戦前の水準をほぼ回復した日本経済は、1955年から73年までの間、年平均で10%程度の成長を続けた (①________)。
それによって、国民の所得は増え、くらしが便利になり1950年代後半には三種の神器(②____、③____、④____)が、1960年代後半には3C(⑤____、⑥____、⑦____)が普及した。
しかし、その一方でさまざまな社会問題も発生し、農村では⑧____化が進み、逆に過密になった都市では住宅不足などが起こった。
また、大気汚染や水質汚濁などの⑨____ も深刻化した。
被害を受けた住民は、四大公害裁判(⑩____、⑪____、⑫____、⑬____)で、 公害を発生させた企業に勝訴した。
その後、1967年に⑭____法が制定され、1971年には⑮____が設置された。
1973年の⑯________によって、①‗‗‗‗‗‗‗‗‗‗は終わりを告げた。
【高校数学】数Ⅰ-24 集合①

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎$U={1.2.3.4.5.6.7.8.9.10}$を全体集合とする。
$U$の部分集合$A={1.2.3.4.8},B={1.3.5.7.9}$について、次の集合を求めよう。
①$A \cap B$
②$A \cup B$
③$\overline{ A } \cap \overline{ B }$
④$ A \cup \overline{ B }$
⑤$\overline{ A } \cap B $
⑥$\overline{ A \cup B} $
この動画を見る
◎$U={1.2.3.4.5.6.7.8.9.10}$を全体集合とする。
$U$の部分集合$A={1.2.3.4.8},B={1.3.5.7.9}$について、次の集合を求めよう。
①$A \cap B$
②$A \cup B$
③$\overline{ A } \cap \overline{ B }$
④$ A \cup \overline{ B }$
⑤$\overline{ A } \cap B $
⑥$\overline{ A \cup B} $


