 とある男が授業をしてみた
とある男が授業をしてみた
 とある男が授業をしてみた
とある男が授業をしてみた
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【数学】中3-69 三平方・空間図形への利用③(円錐編)

単元:
#数学(中学生)#中1数学#中3数学#空間図形#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の円錐の体積は?
②直線ACを回転の軸として一回転させてできる立体の体積は?
◎右の展開図を組み立てたときにできる立体について求めよう!
③高さは?
④体積は?
※図は動画内参照
この動画を見る
①右の円錐の体積は?
②直線ACを回転の軸として一回転させてできる立体の体積は?
◎右の展開図を組み立てたときにできる立体について求めよう!
③高さは?
④体積は?
※図は動画内参照
【数学】中3-68 三平方・空間図形への利用②(角錐編)

単元:
#数学(中学生)#中1数学#中3数学#空間図形#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎右の正四角錐についてもとめよう!
①OHの長さは?
②体積は?
③表面積は?
※図は動画内参照
この動画を見る
◎右の正四角錐についてもとめよう!
①OHの長さは?
②体積は?
③表面積は?
※図は動画内参照
【数学】中3-66 三平方・平面図形への利用④(座標編)

単元:
#数学(中学生)#中1数学#中2数学#中3数学#三平方の定理#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の座標をもつ点間の距離は?
①A(2,5)、B(-3,1)
②A(1,4)、B(3,-2)
③次の座標をもつ3点を頂点とする三角形はどんな三角形?
A(-4,1)、B(2,5)、C(6,-1)
この動画を見る
◎次の座標をもつ点間の距離は?
①A(2,5)、B(-3,1)
②A(1,4)、B(3,-2)
③次の座標をもつ3点を頂点とする三角形はどんな三角形?
A(-4,1)、B(2,5)、C(6,-1)
【数学】中3-67 三平方・空間図形への利用①(基本編)

単元:
#数学(中学生)#中1数学#中3数学#空間図形#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
直方体の対角線の長さをℓとすると
①$ℓ^2=$________が成り立つ。
◎右の直方体についてもとめよう!
②AGの長さは?
③EGの長さは?
④$\triangle AEG$の面積は?
※図は動画内参照
この動画を見る
直方体の対角線の長さをℓとすると
①$ℓ^2=$________が成り立つ。
◎右の直方体についてもとめよう!
②AGの長さは?
③EGの長さは?
④$\triangle AEG$の面積は?
※図は動画内参照
【数学】中3-64 三平方・平面図形への利用②(面積編)
単元:
#数学(中学生)#中1数学#中3数学#三平方の定理#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
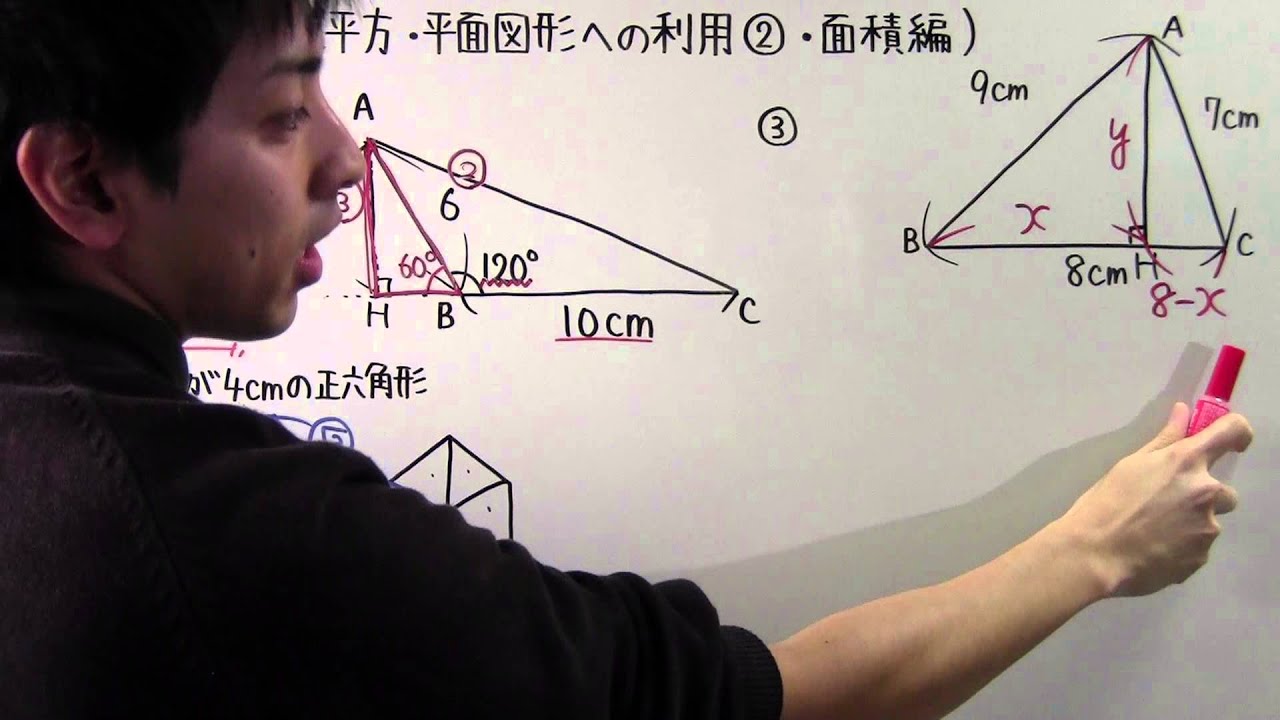
◎面積をもとめよう!
①
②1辺の長さが4cmの正六角形
③
※図は動画内参照
この動画を見る
◎面積をもとめよう!
①
②1辺の長さが4cmの正六角形
③
※図は動画内参照
【数学】中3-65 三平方・平面図形への利用③(円とのコラボ編)
単元:
#数学(中学生)#中3数学#円#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
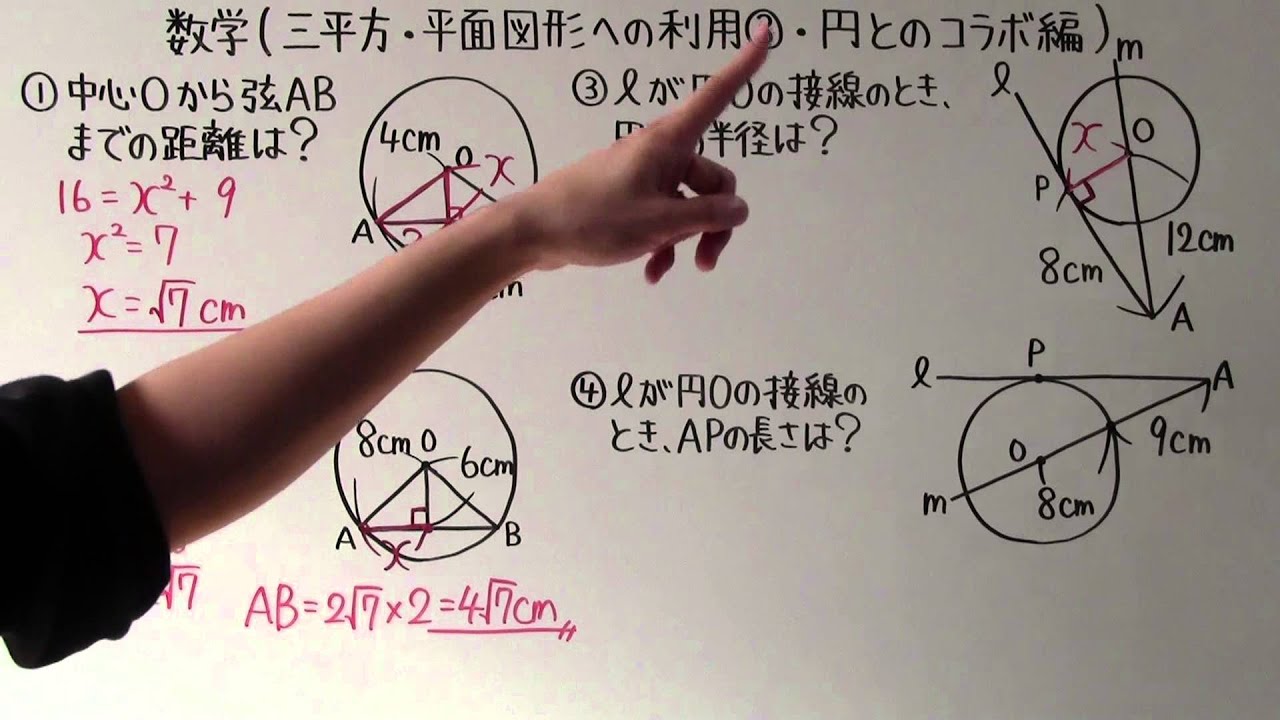
①中心Oから弦ABまでの距離は?
②弦ABの長さは?
③ℓが円Oの接線のとき、円Oの半径は?
④ℓが円Oの接線のとき、APの長さは?
※図は動画内参照
この動画を見る
①中心Oから弦ABまでの距離は?
②弦ABの長さは?
③ℓが円Oの接線のとき、円Oの半径は?
④ℓが円Oの接線のとき、APの長さは?
※図は動画内参照
【数学】中3-63 三平方・平面図形への利用①(基本編)

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
三角定規の辺の比は暗記しておこう!
①
②
◎xの値をもとめよう!
(③~⑤)
⑥1辺の長さが6cmの正三角形の面積は?
※①~⑤の図は動画内参照
この動画を見る
三角定規の辺の比は暗記しておこう!
①
②
◎xの値をもとめよう!
(③~⑤)
⑥1辺の長さが6cmの正三角形の面積は?
※①~⑤の図は動画内参照
【数学】中3-62 三平方の定理②(練習編)

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①2辺の長さが4cm、8cmの正方形の対角線の長さは?
②2つの対角線の長さが12cm、16cmのひし形の1辺の長さは?
③BDの長さは?
※図は動画内参照
④次の長さを③辺とすると㋐~㋒の中で直角三角形はどれ?
㋐5cm、8cm、6cm
㋑$2\sqrt{ 2 }cm、2\sqrt{ 3 }cm、2\sqrt{ 5 }cm$
㋒$2cm、2\sqrt{ 3 }cm、3cm$
この動画を見る
①2辺の長さが4cm、8cmの正方形の対角線の長さは?
②2つの対角線の長さが12cm、16cmのひし形の1辺の長さは?
③BDの長さは?
※図は動画内参照
④次の長さを③辺とすると㋐~㋒の中で直角三角形はどれ?
㋐5cm、8cm、6cm
㋑$2\sqrt{ 2 }cm、2\sqrt{ 3 }cm、2\sqrt{ 5 }cm$
㋒$2cm、2\sqrt{ 3 }cm、3cm$
【数学】中3-61 三平方の定理①(基本編)

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
左の直角三角形について①________が成り立つ。
これを三平本の定理という。
◎xの長さをもとめよう!
※図は動画内参照
この動画を見る
左の直角三角形について①________が成り立つ。
これを三平本の定理という。
◎xの長さをもとめよう!
※図は動画内参照
【小5 算数】 小5-40 分数のたし算・ひき算③ ・ 小数とのコラボ編
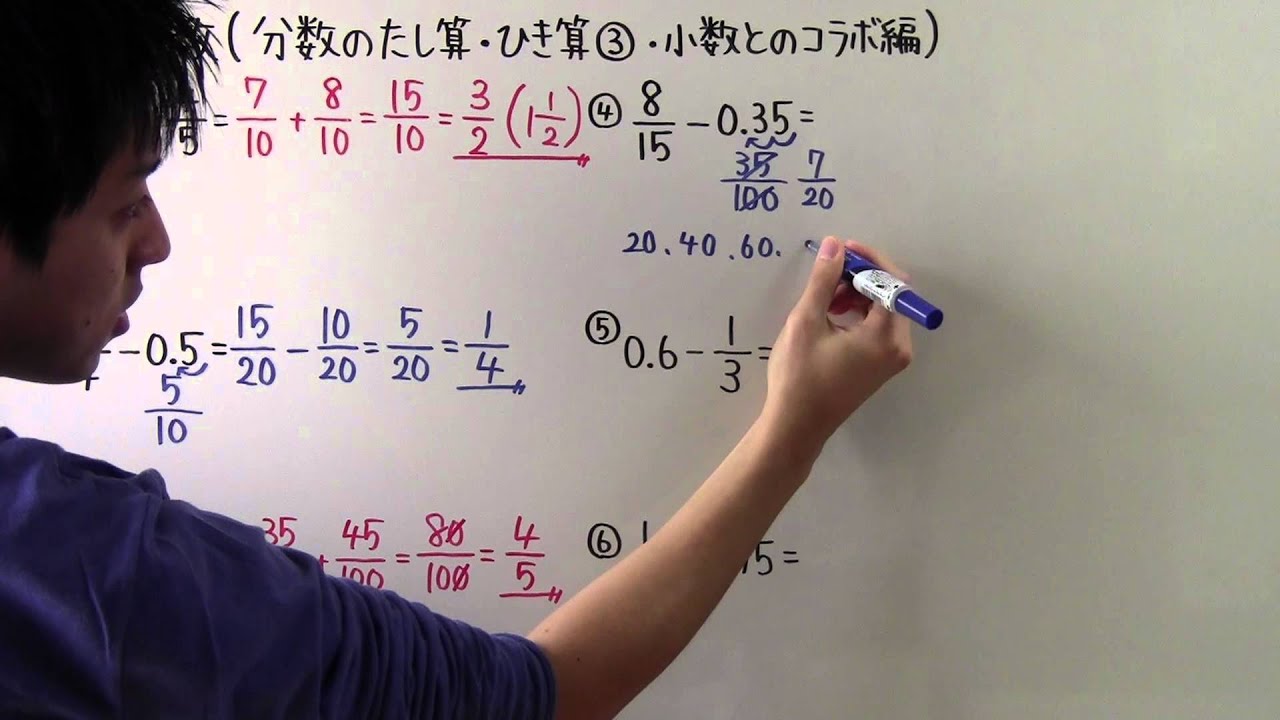
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$0.7+\displaystyle \frac{4}{5}=$
②$3\displaystyle \frac{3}{4}-0.5=$
③$2\displaystyle \frac{7}{20}+0.45=$
④$1\displaystyle \frac{8}{15}-0.35=$
⑤$0.6-\displaystyle \frac{1}{3}=$
⑥$\displaystyle \frac{1}{3}+0.75=$
この動画を見る
①$0.7+\displaystyle \frac{4}{5}=$
②$3\displaystyle \frac{3}{4}-0.5=$
③$2\displaystyle \frac{7}{20}+0.45=$
④$1\displaystyle \frac{8}{15}-0.35=$
⑤$0.6-\displaystyle \frac{1}{3}=$
⑥$\displaystyle \frac{1}{3}+0.75=$
【小5 算数】 小5-39 分数のたし算・ひき算② ・ 帯分数編
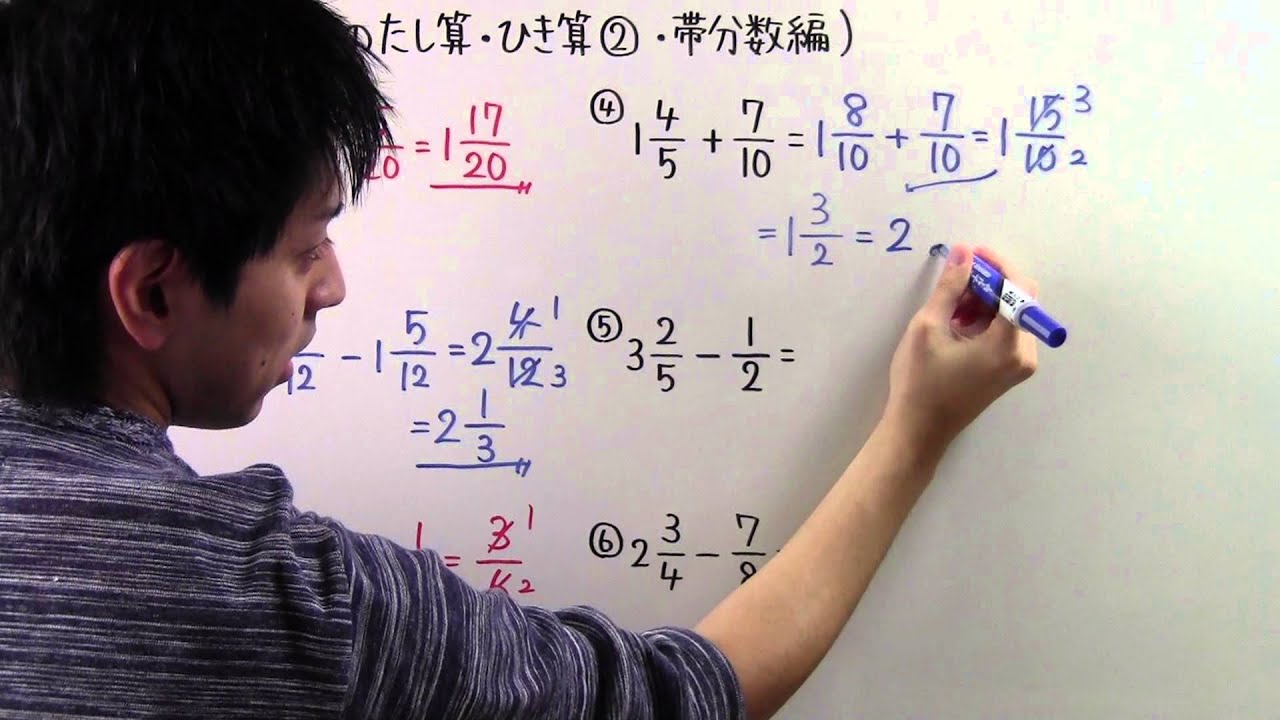
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$1\displaystyle \frac{3}{5}+\displaystyle \frac{1}{4}=$
②$3\displaystyle \frac{3}{4}-1\displaystyle \frac{5}{12}=$
③$2\displaystyle \frac{2}{3}-2\displaystyle \frac{1}{6}=$
④$1\displaystyle \frac{4}{5}+\displaystyle \frac{7}{10}=$
⑤$3\displaystyle \frac{2}{5}-\displaystyle \frac{1}{2}=$
⑥$2\displaystyle \frac{3}{4}-\displaystyle \frac{7}{8}=$
この動画を見る
①$1\displaystyle \frac{3}{5}+\displaystyle \frac{1}{4}=$
②$3\displaystyle \frac{3}{4}-1\displaystyle \frac{5}{12}=$
③$2\displaystyle \frac{2}{3}-2\displaystyle \frac{1}{6}=$
④$1\displaystyle \frac{4}{5}+\displaystyle \frac{7}{10}=$
⑤$3\displaystyle \frac{2}{5}-\displaystyle \frac{1}{2}=$
⑥$2\displaystyle \frac{3}{4}-\displaystyle \frac{7}{8}=$
【小5 算数】 小5-38 分数のたし算・ひき算① ・ 基本編

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$\displaystyle \frac{3}{7}+\displaystyle \frac{2}{7}=$
②$\displaystyle \frac{2}{3}+\displaystyle \frac{1}{2}=$
③$\displaystyle \frac{7}{5}-\displaystyle \frac{2}{3}=$
④$\displaystyle \frac{4}{5}-\displaystyle \frac{3}{10}=$
⑤$\displaystyle \frac{5}{14}+\displaystyle \frac{1}{2}=$
⑥$\displaystyle \frac{2}{3}-\displaystyle \frac{4}{9}=$
⑦$\displaystyle \frac{3}{4}-\displaystyle \frac{1}{6}+\displaystyle \frac{2}{3}=$
この動画を見る
①$\displaystyle \frac{3}{7}+\displaystyle \frac{2}{7}=$
②$\displaystyle \frac{2}{3}+\displaystyle \frac{1}{2}=$
③$\displaystyle \frac{7}{5}-\displaystyle \frac{2}{3}=$
④$\displaystyle \frac{4}{5}-\displaystyle \frac{3}{10}=$
⑤$\displaystyle \frac{5}{14}+\displaystyle \frac{1}{2}=$
⑥$\displaystyle \frac{2}{3}-\displaystyle \frac{4}{9}=$
⑦$\displaystyle \frac{3}{4}-\displaystyle \frac{1}{6}+\displaystyle \frac{2}{3}=$
【小5 算数】 小5-37 分数の技④ ・ 時間と分数編

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
分→時間、秒→分にするときには、分母に①____をつける!
◎時間の単位を変えてみよう!
②7分=____________時間
③15分=____________時間
④36秒=____________分
⑤150秒=____________分
⑥1時間18分=____________時間
⑦3時間=____________分
⑧7分=____________秒
⑨168秒=____________分
この動画を見る
分→時間、秒→分にするときには、分母に①____をつける!
◎時間の単位を変えてみよう!
②7分=____________時間
③15分=____________時間
④36秒=____________分
⑤150秒=____________分
⑥1時間18分=____________時間
⑦3時間=____________分
⑧7分=____________秒
⑨168秒=____________分
【小5 算数】 小5-36 分数の技③ ・ 通分編

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①____をそろえることを通分といって②____算を使うんだ!
◎( )の中の分数を通分しよう!
③$(\displaystyle \frac{2}{3},\displaystyle \frac{1}{4})=( , )$
④$(\displaystyle \frac{3}{2},\displaystyle \frac{5}{8})=( , )$
⑤$(1\displaystyle \frac{5}{6},2\displaystyle \frac{1}{4})=( , )$
⑥$(\displaystyle \frac{1}{2},\displaystyle \frac{2}{3},\displaystyle \frac{5}{9})=( , )$
◎$□$にあてはまる等号や不等号を書こう!
⑦$\displaystyle \frac{3}{5}□\displaystyle \frac{2}{3}$
⑧$\displaystyle \frac{3}{4}□\displaystyle \frac{7}{12}$
⑨$\displaystyle \frac{10}{15}□\displaystyle \frac{6}{9}$
この動画を見る
①____をそろえることを通分といって②____算を使うんだ!
◎( )の中の分数を通分しよう!
③$(\displaystyle \frac{2}{3},\displaystyle \frac{1}{4})=( , )$
④$(\displaystyle \frac{3}{2},\displaystyle \frac{5}{8})=( , )$
⑤$(1\displaystyle \frac{5}{6},2\displaystyle \frac{1}{4})=( , )$
⑥$(\displaystyle \frac{1}{2},\displaystyle \frac{2}{3},\displaystyle \frac{5}{9})=( , )$
◎$□$にあてはまる等号や不等号を書こう!
⑦$\displaystyle \frac{3}{5}□\displaystyle \frac{2}{3}$
⑧$\displaystyle \frac{3}{4}□\displaystyle \frac{7}{12}$
⑨$\displaystyle \frac{10}{15}□\displaystyle \frac{6}{9}$
【小5 算数】 小5-35 分数の技② ・ 約分編

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
分母と分子を同じ数で①____ことを約分っていうんだ!
◎次の文数を約分しよう!
②$\displaystyle \frac{4}{6}=$
③$\displaystyle \frac{24}{16}=$
④$2\displaystyle \frac{15}{18}=$
⑤$\displaystyle \frac{21}{28}=$
⑥$\displaystyle \frac{56}{72}=$
⑦$\displaystyle \frac{84}{156}=$
⑧次の文数の中で$\displaystyle \frac{9}{12}$と同じ大きさの分数に〇をつけよう!
$\displaystyle \frac{4}{5}, \displaystyle \frac{6}{8}, \displaystyle \frac{10}{15},
\displaystyle \frac{10}{13}, \displaystyle \frac{3}{4}$
この動画を見る
分母と分子を同じ数で①____ことを約分っていうんだ!
◎次の文数を約分しよう!
②$\displaystyle \frac{4}{6}=$
③$\displaystyle \frac{24}{16}=$
④$2\displaystyle \frac{15}{18}=$
⑤$\displaystyle \frac{21}{28}=$
⑥$\displaystyle \frac{56}{72}=$
⑦$\displaystyle \frac{84}{156}=$
⑧次の文数の中で$\displaystyle \frac{9}{12}$と同じ大きさの分数に〇をつけよう!
$\displaystyle \frac{4}{5}, \displaystyle \frac{6}{8}, \displaystyle \frac{10}{15},
\displaystyle \frac{10}{13}, \displaystyle \frac{3}{4}$
【小5 算数】 小5-34 分数の技① ・ 基本編

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
分数は、分母と分子を①____でかけたり、わったりしていいんだよ!
◎$□$にあてはまる数を書こう!
②$\displaystyle \frac{3}{4}=\displaystyle \frac{□}{8}$
③$\displaystyle \frac{2}{3}=\displaystyle \frac{□}{9}$
④$\displaystyle \frac{10}{12}=\displaystyle \frac{□}{6}$
⑤$\displaystyle \frac{1}{5}=\displaystyle \frac{□}{10}=\displaystyle \frac{4}{□}$
⑥$\displaystyle \frac{6}{9}=\displaystyle \frac{□}{3}=\displaystyle \frac{□}{15}$
⑦$\displaystyle \frac{6}{12}=\displaystyle \frac{□}{14}$
この動画を見る
分数は、分母と分子を①____でかけたり、わったりしていいんだよ!
◎$□$にあてはまる数を書こう!
②$\displaystyle \frac{3}{4}=\displaystyle \frac{□}{8}$
③$\displaystyle \frac{2}{3}=\displaystyle \frac{□}{9}$
④$\displaystyle \frac{10}{12}=\displaystyle \frac{□}{6}$
⑤$\displaystyle \frac{1}{5}=\displaystyle \frac{□}{10}=\displaystyle \frac{4}{□}$
⑥$\displaystyle \frac{6}{9}=\displaystyle \frac{□}{3}=\displaystyle \frac{□}{15}$
⑦$\displaystyle \frac{6}{12}=\displaystyle \frac{□}{14}$
【小5 算数】 小5-33 多角形の角
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
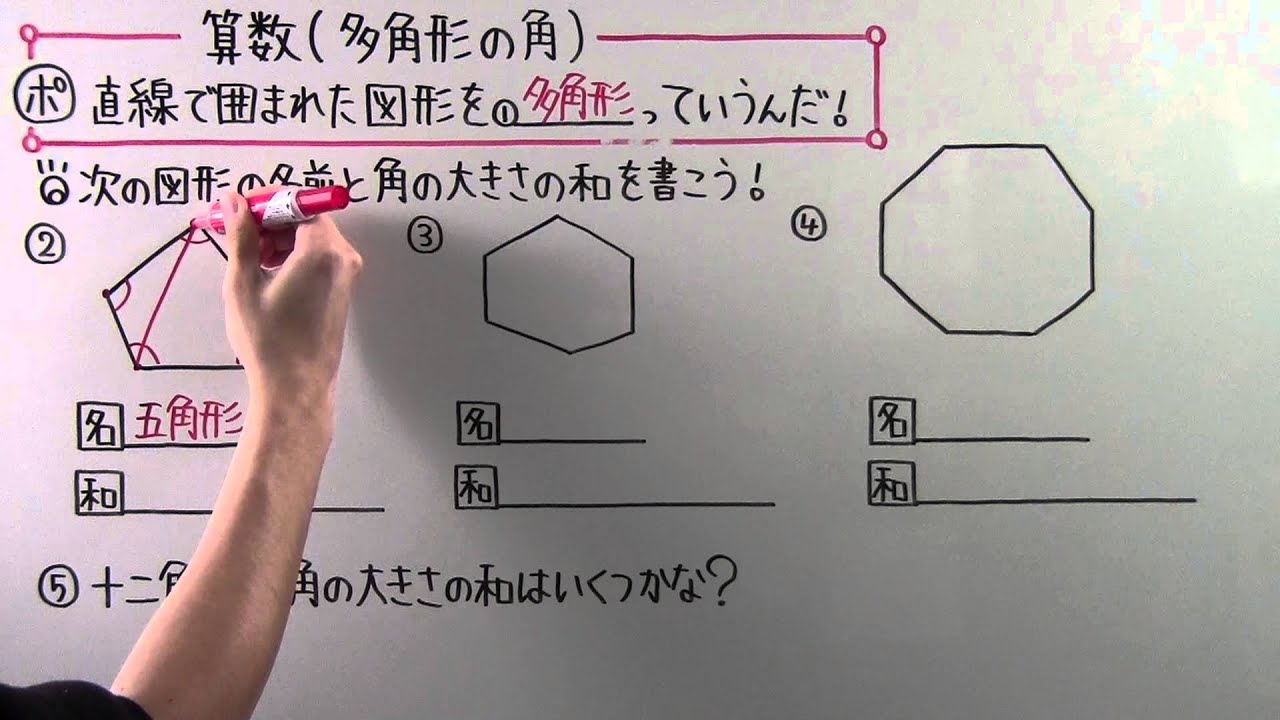
直線で囲まれた図形を①____っていうんだ!
◎次の図形の名前と角の大きさの和を書こう!
②
[名]____
[和]________
③
[名]____
[和]________
④
[名]____
[和]________
※図は動画内参照
⑤十二角形の角の大きさの和はいくつかな?
この動画を見る
直線で囲まれた図形を①____っていうんだ!
◎次の図形の名前と角の大きさの和を書こう!
②
[名]____
[和]________
③
[名]____
[和]________
④
[名]____
[和]________
※図は動画内参照
⑤十二角形の角の大きさの和はいくつかな?
【小5 算数】 小5-31 三角形の角

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
3つの角度をたすと①____になるよ!
◎角度の計算で求めよう!
※図は動画内参照
この動画を見る
3つの角度をたすと①____になるよ!
◎角度の計算で求めよう!
※図は動画内参照
【小5 算数】 小5-32 四角形の角
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
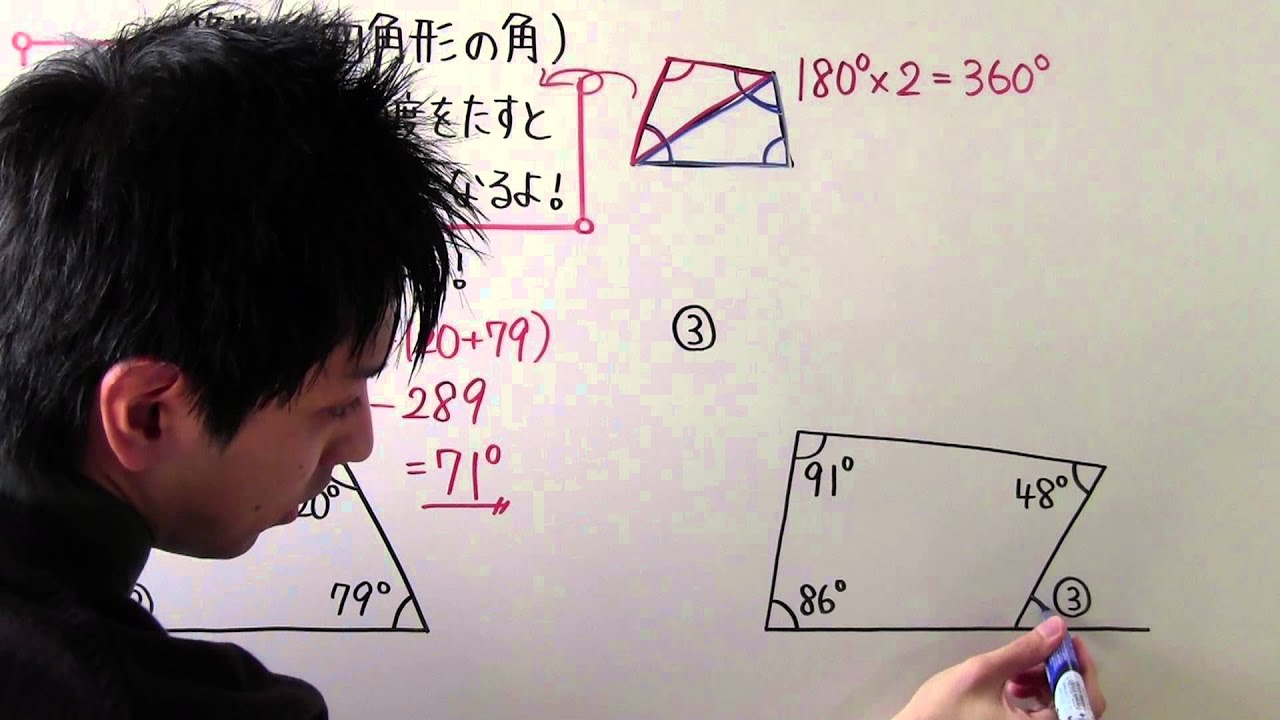
4つの角度をたすと①____になるよ!
◎角度の計算で求めよう!
※図は動画内参照
この動画を見る
4つの角度をたすと①____になるよ!
◎角度の計算で求めよう!
※図は動画内参照
【数学】中2-60 証明のしくみ

単元:
#数学(中学生)#中2数学#平行と合同#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\boxed{1}$
[仮]・・・①______
[結]・・・②______
$\boxed{2}$どれとどれの合同でやるの?
③______と______
$\boxed{3}$すでに同じだと分かっている辺と角に印をつける。
④右上の図に印をつけよう!
$\boxed{4}$合同条件を決める。
⑤_________________
$\boxed{5}$書く!!
⑥$AO=CO,\triangle OAB= \triangle OCD$ならば、
$AB=CD$であることを証明しよう!
【宣言】
_________________で
【理由】
____より _________________・・・①
_________________・・・②
____より _________________・・・③
【合同条件】
①、②、③より _________________から
_________________
【結論】
____より _________________
※図は動画内参照
この動画を見る
$\boxed{1}$
[仮]・・・①______
[結]・・・②______
$\boxed{2}$どれとどれの合同でやるの?
③______と______
$\boxed{3}$すでに同じだと分かっている辺と角に印をつける。
④右上の図に印をつけよう!
$\boxed{4}$合同条件を決める。
⑤_________________
$\boxed{5}$書く!!
⑥$AO=CO,\triangle OAB= \triangle OCD$ならば、
$AB=CD$であることを証明しよう!
【宣言】
_________________で
【理由】
____より _________________・・・①
_________________・・・②
____より _________________・・・③
【合同条件】
①、②、③より _________________から
_________________
【結論】
____より _________________
※図は動画内参照
【数学】中2-59 仮定と結論

単元:
#数学(中学生)#中2数学#平行と合同
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
『$a=b,b=c$ならば、$a=c$である』の文の、
仮定は①____、結論は②____。
ちなみに証明するとき、仮定は③____アイテムで、
結論は④____アイテムなんだ!
◎次の文の仮定には____、結論には‗‗‗‗‗‗‗を引こう!
⑤$\triangle ABC \equiv \triangle DEF$ならば、$\angle BAC=\angle EDF$である。
⑥$ℓ//m,m//n$ならば、$ℓ//n$である。
⑦2つの直線が平行ならば、錯角は等しい。
⑧$a=b$ならば、$ac=bc$である。
この動画を見る
『$a=b,b=c$ならば、$a=c$である』の文の、
仮定は①____、結論は②____。
ちなみに証明するとき、仮定は③____アイテムで、
結論は④____アイテムなんだ!
◎次の文の仮定には____、結論には‗‗‗‗‗‗‗を引こう!
⑤$\triangle ABC \equiv \triangle DEF$ならば、$\angle BAC=\angle EDF$である。
⑥$ℓ//m,m//n$ならば、$ℓ//n$である。
⑦2つの直線が平行ならば、錯角は等しい。
⑧$a=b$ならば、$ac=bc$である。
【数学】中2-58 三角形の合同③ 合同探し編

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎合同な三角形を記号を使って表し、合同条件も書こう!
①$AB=AD,\angle BAC= \angle DAC$
②$AB=CD,AB//CD$
③$AD=AE,\angle ADC=\angle AEB$
※図は動画内参照
この動画を見る
◎合同な三角形を記号を使って表し、合同条件も書こう!
①$AB=AD,\angle BAC= \angle DAC$
②$AB=CD,AB//CD$
③$AD=AE,\angle ADC=\angle AEB$
※図は動画内参照
【数学】中2-57 三角形の合同② 応用編

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の三角形はすべて合同といえる?
①一辺の長さが6cmの正方形
②2つの内角が60°と70°の三角形
③等しい辺の長さが10cmの二等辺三角形
◎$\triangle ABC$と$\triangle DFE$で、あと1つどんな条件を加えれば合同といえる?
④$AB=DE、AC=DF$
⑤$\angle ABC= \angle DEF、BC=EF$
※図は動画内参照
この動画を見る
◎次の三角形はすべて合同といえる?
①一辺の長さが6cmの正方形
②2つの内角が60°と70°の三角形
③等しい辺の長さが10cmの二等辺三角形
◎$\triangle ABC$と$\triangle DFE$で、あと1つどんな条件を加えれば合同といえる?
④$AB=DE、AC=DF$
⑤$\angle ABC= \angle DEF、BC=EF$
※図は動画内参照
【数学】中2-56 三角形の合同① 基本編

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
【ポイント】
三角形の合同条件は3種類!!
①____がそれぞれ等しいとき
②____________がそれぞれ等しいとき
③____________がそれぞれ等しいとき
④右の三角形から合同なものを選び、記号を使って表そう!
(合同条件はポイントの番号から選ぶ)
※図は動画内参照
この動画を見る
【ポイント】
三角形の合同条件は3種類!!
①____がそれぞれ等しいとき
②____________がそれぞれ等しいとき
③____________がそれぞれ等しいとき
④右の三角形から合同なものを選び、記号を使って表そう!
(合同条件はポイントの番号から選ぶ)
※図は動画内参照
【数学】中2-55 角度チャレンジ Lv.3
【数学】中2-54 角度チャレンジ Lv.2

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
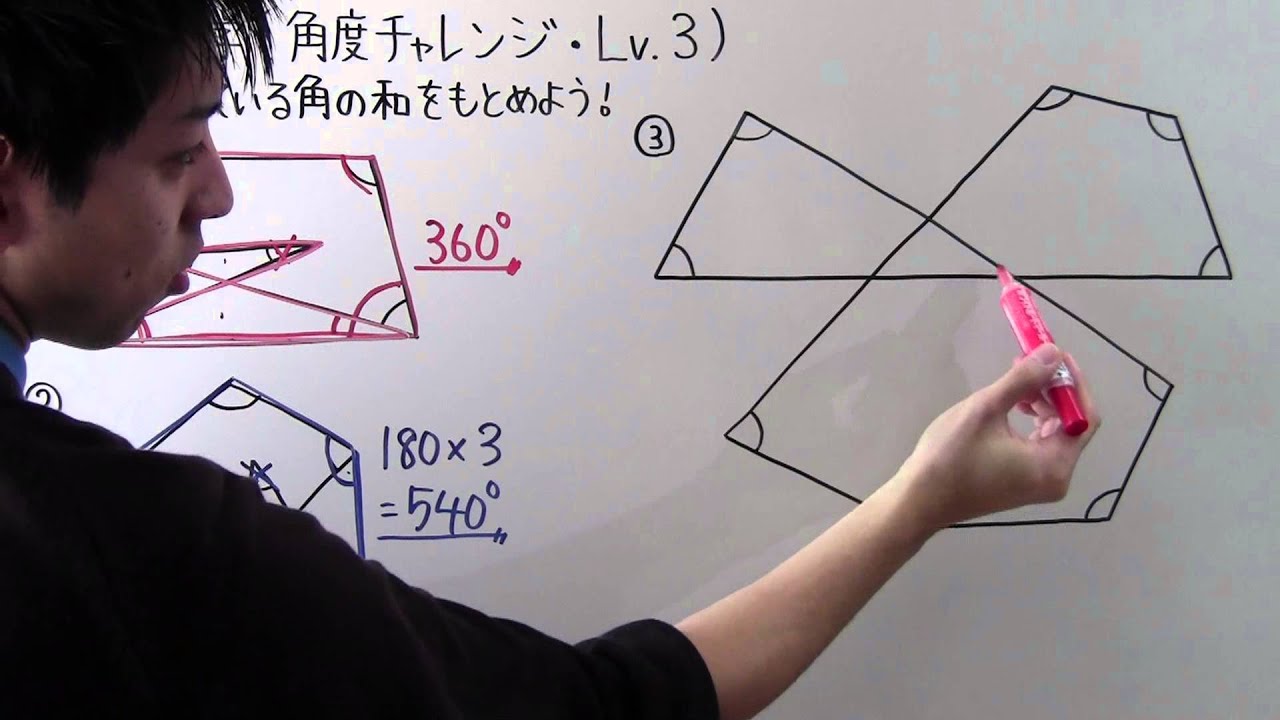
◎$\angle x,\angle y$の大きさをもとめよう!
①
②
③正五角形$ABCDE$
④$AB//CD,\angle BPQ$の二等分線と$\angle DQP$の二等分線の交点を$R$とする。
※図は動画内参照
この動画を見る
◎$\angle x,\angle y$の大きさをもとめよう!
①
②
③正五角形$ABCDE$
④$AB//CD,\angle BPQ$の二等分線と$\angle DQP$の二等分線の交点を$R$とする。
※図は動画内参照
【数学】中2-53 角度チャレンジ Lv.1

【数学】中2-52 多角形の内角と外角の和② 計算編

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①五角形の内角の和は?
②正十角形の1つの内角の大きさは?
③内角の和が1260°になるのは何角形?
④正十八角形の1つの外角の大きさは?
⑤1つの外角の大きさが24°になるのは正何角形?
⑥1つの内角の大きさが162°になるのは正何角形?
⑦内角の和が外角の和の6倍である多角形は何角形?
この動画を見る
①五角形の内角の和は?
②正十角形の1つの内角の大きさは?
③内角の和が1260°になるのは何角形?
④正十八角形の1つの外角の大きさは?
⑤1つの外角の大きさが24°になるのは正何角形?
⑥1つの内角の大きさが162°になるのは正何角形?
⑦内角の和が外角の和の6倍である多角形は何角形?
【数学】中2-51 多角形の内角と外角の和① 基本編
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
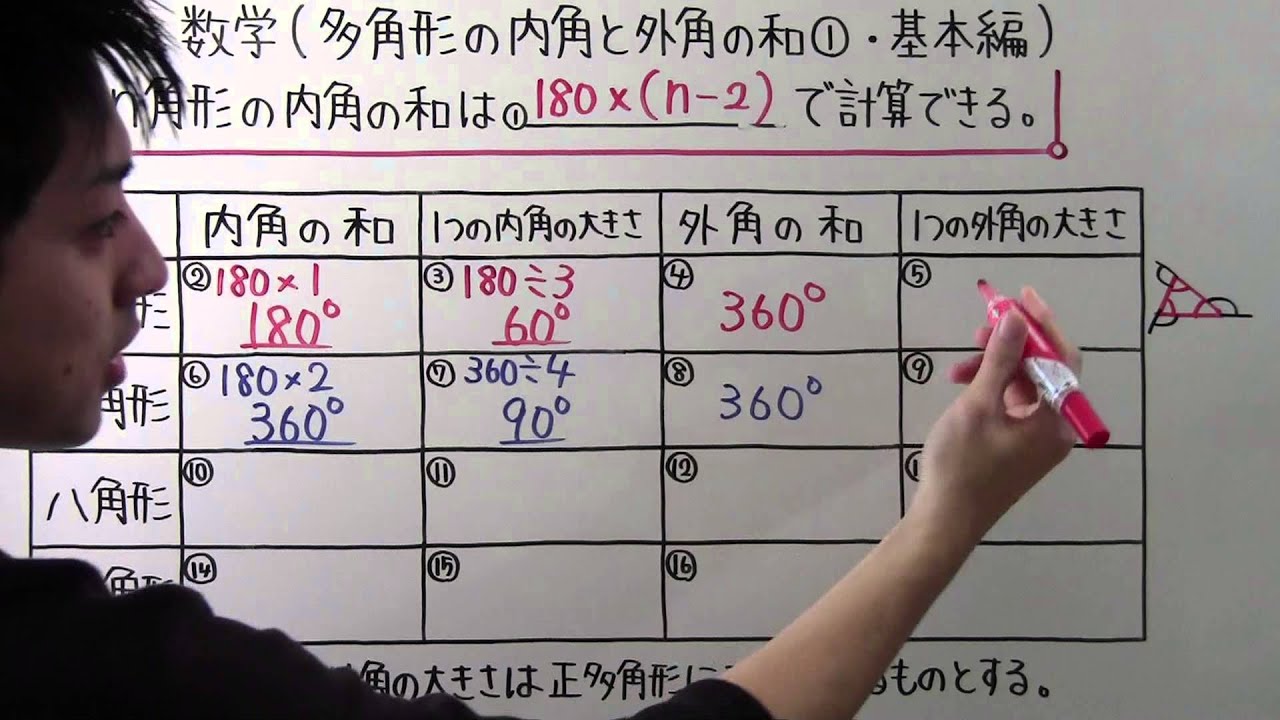
n角形の内角の和は①_____で計算できる。
1つの内角と外角の大きさは正多角形について考えるものとする。
※表は動画内参照
この動画を見る
n角形の内角の和は①_____で計算できる。
1つの内角と外角の大きさは正多角形について考えるものとする。
※表は動画内参照
【数学】中2-50 鋭角三角形と鈍角三角形

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
0°から90°の角を①____、90°の角を②____、90°から180°の角を③____という。
①____三角形は『④____つの内角が⑤____である三角形』、②____三角形は『⑥__つの内角が⑦__である三角形』、③____三角形は『⑧__つの内角が⑨__である三角形』!!
◎2つの内角が次の大きさのとき、どの三角形になる?
⑩32°、78°
⑪15°、123°
⑫35°、24°
⑬51°、39°
この動画を見る
0°から90°の角を①____、90°の角を②____、90°から180°の角を③____という。
①____三角形は『④____つの内角が⑤____である三角形』、②____三角形は『⑥__つの内角が⑦__である三角形』、③____三角形は『⑧__つの内角が⑨__である三角形』!!
◎2つの内角が次の大きさのとき、どの三角形になる?
⑩32°、78°
⑪15°、123°
⑫35°、24°
⑬51°、39°


