受験算数の森
受験算数の森
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
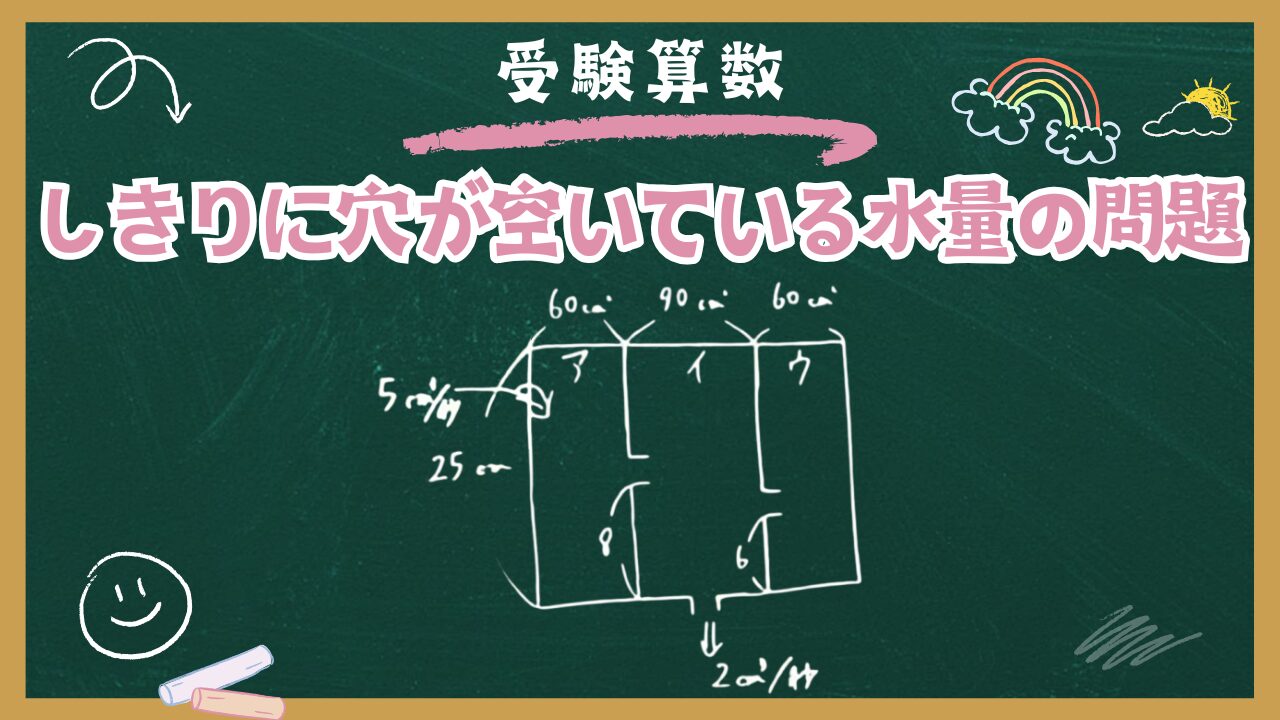
【受験算数】変化のグラフ：⑧しきりに穴がある
単元：
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
受験算数の森
問題文全文(内容文)：
大問1
縦10cm、横21cm、高さ25cmの直方体の容器が図のように、2枚の板で左から6cm、さらに 9cmのところで、ア、イ、ウに垂直に区切られ ています。左の板には下から8cm、右の板には下から6cmのところにそれぞれ穴があいています。また、イの底には水が入っていれば、毎秒 2㎤で水が出ていく仕掛けの穴があいていま す。いま、アのところに毎秒5㎤で水を入れはじめたとします。ただし、容器、板の厚さは考えずに、板の穴はその位置まで達した水がとどまることなく、すべて流れ出るのに十分な大きさの穴とします。次の問いに答えなさい。
(1) アのところの深さが5㎝になるのは、水を入れはじめてから何秒後ですか。
(2) 3分36秒後のイのところの深さは、何㎝ですか。
(3) ウのところの深さが1cmになるのは、何分何秒後ですか。
(4) 水を入れはじめて5分16秒後に水を入れるのをやめ、3分間止めてからふたたび水を入れはじめました。ふたたび水を入れはじめてから、さらに2分後、ア、 イ、ウの容器には、それぞれ何cmの深さまで水が入っていますか。
大問2
縦10cm、横20cm、高さ18cmの直方体の容器が図のように、2枚の板で左から6cm、さらに 8cmのところで、ア、イ、ウに垂直に区切られ ています。左の板には下から10cm、右の板には下から8cmのところにそれぞれ穴があいています。また、イの底には水が入っていれば、毎秒 2㎤で水が出ていく仕掛けの穴があいていま す。いま、アのところに毎秒6㎤で水を入れはじめたとします。ただし、容器、板の厚さは考えずに、板の穴はその位置まで達した水がとどまることなく、すべて流れ出るのに十分な大きさの穴とします。次の問いに答えなさい。
(1) アのところの深さが6㎝になるのは、水を入れはじめてから何秒後ですか。
(2) 2分40秒後のイのところの深さは、何㎝ですか。
(3) ウのところの深さが1cmになるのは、何分何秒後ですか。
(4) 水を入れはじめて4分50秒後に水を入れるのをやめ、4分間止めてからふたたび水を入れはじめました。ふたたび水を入れはじめてから、さらに3分後、ア、 イ、ウの容器には、それぞれ何cmの深さまで水が入っていますか。
この動画を見る
大問1
縦10cm、横21cm、高さ25cmの直方体の容器が図のように、2枚の板で左から6cm、さらに 9cmのところで、ア、イ、ウに垂直に区切られ ています。左の板には下から8cm、右の板には下から6cmのところにそれぞれ穴があいています。また、イの底には水が入っていれば、毎秒 2㎤で水が出ていく仕掛けの穴があいていま す。いま、アのところに毎秒5㎤で水を入れはじめたとします。ただし、容器、板の厚さは考えずに、板の穴はその位置まで達した水がとどまることなく、すべて流れ出るのに十分な大きさの穴とします。次の問いに答えなさい。
(1) アのところの深さが5㎝になるのは、水を入れはじめてから何秒後ですか。
(2) 3分36秒後のイのところの深さは、何㎝ですか。
(3) ウのところの深さが1cmになるのは、何分何秒後ですか。
(4) 水を入れはじめて5分16秒後に水を入れるのをやめ、3分間止めてからふたたび水を入れはじめました。ふたたび水を入れはじめてから、さらに2分後、ア、 イ、ウの容器には、それぞれ何cmの深さまで水が入っていますか。
大問2
縦10cm、横20cm、高さ18cmの直方体の容器が図のように、2枚の板で左から6cm、さらに 8cmのところで、ア、イ、ウに垂直に区切られ ています。左の板には下から10cm、右の板には下から8cmのところにそれぞれ穴があいています。また、イの底には水が入っていれば、毎秒 2㎤で水が出ていく仕掛けの穴があいていま す。いま、アのところに毎秒6㎤で水を入れはじめたとします。ただし、容器、板の厚さは考えずに、板の穴はその位置まで達した水がとどまることなく、すべて流れ出るのに十分な大きさの穴とします。次の問いに答えなさい。
(1) アのところの深さが6㎝になるのは、水を入れはじめてから何秒後ですか。
(2) 2分40秒後のイのところの深さは、何㎝ですか。
(3) ウのところの深さが1cmになるのは、何分何秒後ですか。
(4) 水を入れはじめて4分50秒後に水を入れるのをやめ、4分間止めてからふたたび水を入れはじめました。ふたたび水を入れはじめてから、さらに3分後、ア、 イ、ウの容器には、それぞれ何cmの深さまで水が入っていますか。
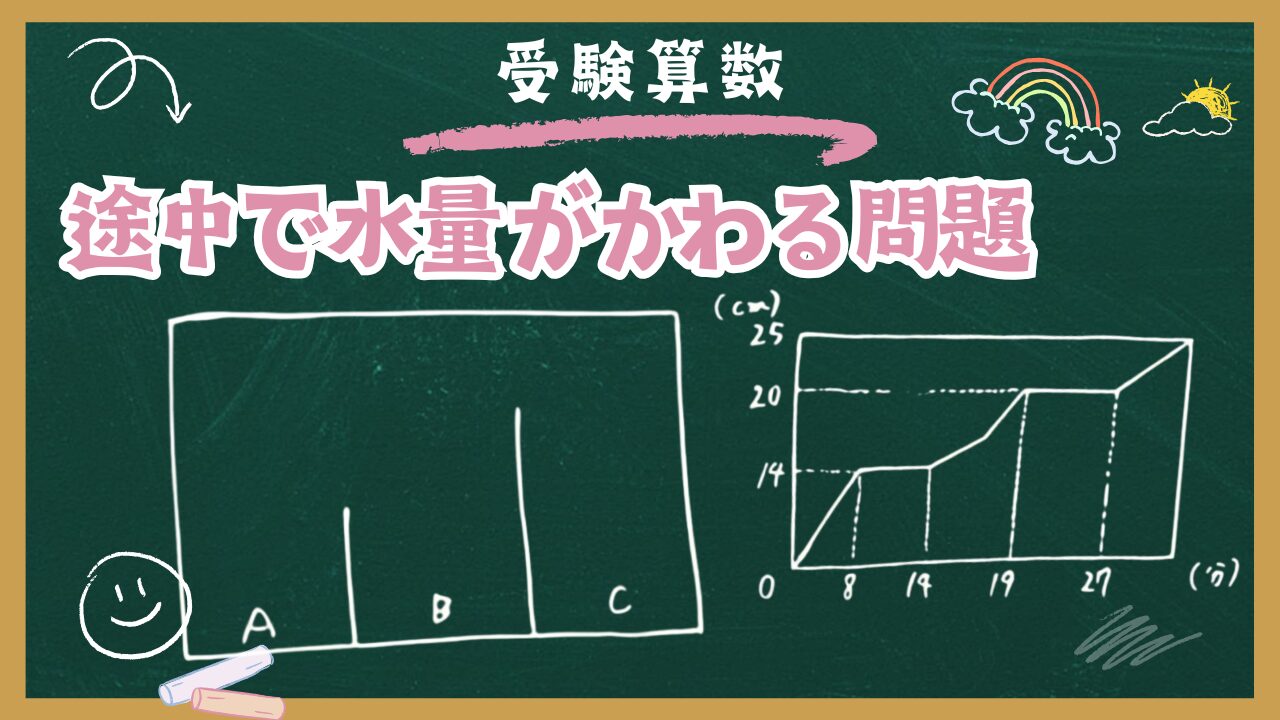
【受験算数】変化のグラフ：⑦途中で水量がかわる
単元：
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
受験算数の森
問題文全文(内容文)：
大問1
下の図のような直方体の水そうに、底面と垂直になるように長方形のしきり板 を2枚入れて底面を3つの長方形に分け、蛇口に近い方からA、B、Cとします。 蛇口からAの部分に、一定の割合で静かに水を入れ始め、途中から入れる水の量を 3/2倍に変えて水そうがいっぱいになるまで水を入れました。このとき、底面がA の部分の水面の高さと、水を入れ始めてからの時間の関係は、下の図2のグラフのようになりました。
次の□に当てはまる数を求めなさい。ただし、しきり板の厚さは考えないも のとします。
(1) 図1の「あ」に当てはまる数は□です。
(2) 蛇口から入れる水の量を3/2倍に変えたのは、水を入れ始めてから□分後です。
(3) 水そうがいっぱいになるのは、水を入れ始めてから□分□秒後です。
大問2
下の図のような直方体の水そうに、底面と垂直になるように長方形のしきり板 を2枚入れて底面を3つの長方形に分け、蛇口に近い方からA、B、Cとします。 蛇口からAの部分に、一定の割合で静かに水を入れ始め、途中から入れる水の量を 5/3倍に変えて水そうがいっぱいになるまで水を入れました。このとき、底面がA の部分の水面の高さと、水を入れ始めてからの時間の関係は、下の図2のグラフのようになりました。
次の□に当てはまる数を求めなさい。ただし、しきり板の厚さは考えないも のとします。
(1) 図1の「あ」に当てはまる数は□です。
(2) 蛇口から入れる水の量を5/3倍に変えたのは、水を入れ始めてから□分後です。
(3) 水そうがいっぱいになるのは、水を入れ始めてから□分□秒後です。
この動画を見る
大問1
下の図のような直方体の水そうに、底面と垂直になるように長方形のしきり板 を2枚入れて底面を3つの長方形に分け、蛇口に近い方からA、B、Cとします。 蛇口からAの部分に、一定の割合で静かに水を入れ始め、途中から入れる水の量を 3/2倍に変えて水そうがいっぱいになるまで水を入れました。このとき、底面がA の部分の水面の高さと、水を入れ始めてからの時間の関係は、下の図2のグラフのようになりました。
次の□に当てはまる数を求めなさい。ただし、しきり板の厚さは考えないも のとします。
(1) 図1の「あ」に当てはまる数は□です。
(2) 蛇口から入れる水の量を3/2倍に変えたのは、水を入れ始めてから□分後です。
(3) 水そうがいっぱいになるのは、水を入れ始めてから□分□秒後です。
大問2
下の図のような直方体の水そうに、底面と垂直になるように長方形のしきり板 を2枚入れて底面を3つの長方形に分け、蛇口に近い方からA、B、Cとします。 蛇口からAの部分に、一定の割合で静かに水を入れ始め、途中から入れる水の量を 5/3倍に変えて水そうがいっぱいになるまで水を入れました。このとき、底面がA の部分の水面の高さと、水を入れ始めてからの時間の関係は、下の図2のグラフのようになりました。
次の□に当てはまる数を求めなさい。ただし、しきり板の厚さは考えないも のとします。
(1) 図1の「あ」に当てはまる数は□です。
(2) 蛇口から入れる水の量を5/3倍に変えたのは、水を入れ始めてから□分後です。
(3) 水そうがいっぱいになるのは、水を入れ始めてから□分□秒後です。
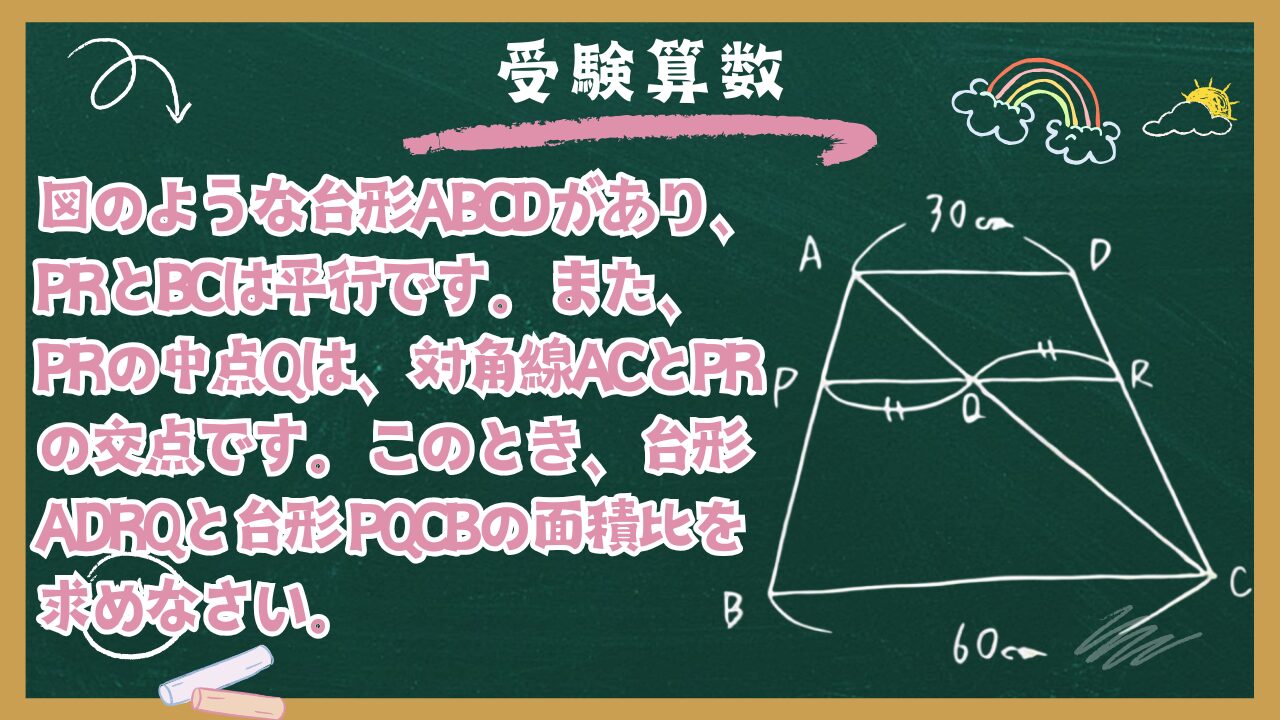
【受験算数】拡大・縮小：⑧2つの台形の面積比
単元：
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
受験算数の森
問題文全文(内容文)：
大問1
図のような台形ABCDがあり、PRとBCは平行です。また、PRの中点Qは、対角線ACとPRの交点です。このとき、台形ADRQと台形 PQCBの面積比を求めなさい。
大問2
図のような台形ABCDがあり、PRとBCは平行です。また、PRの中点Qは、対角線ACとPRの交点です。このとき、台形ADRQと台形 PQCBの面積比を求めなさい。
この動画を見る
大問1
図のような台形ABCDがあり、PRとBCは平行です。また、PRの中点Qは、対角線ACとPRの交点です。このとき、台形ADRQと台形 PQCBの面積比を求めなさい。
大問2
図のような台形ABCDがあり、PRとBCは平行です。また、PRの中点Qは、対角線ACとPRの交点です。このとき、台形ADRQと台形 PQCBの面積比を求めなさい。
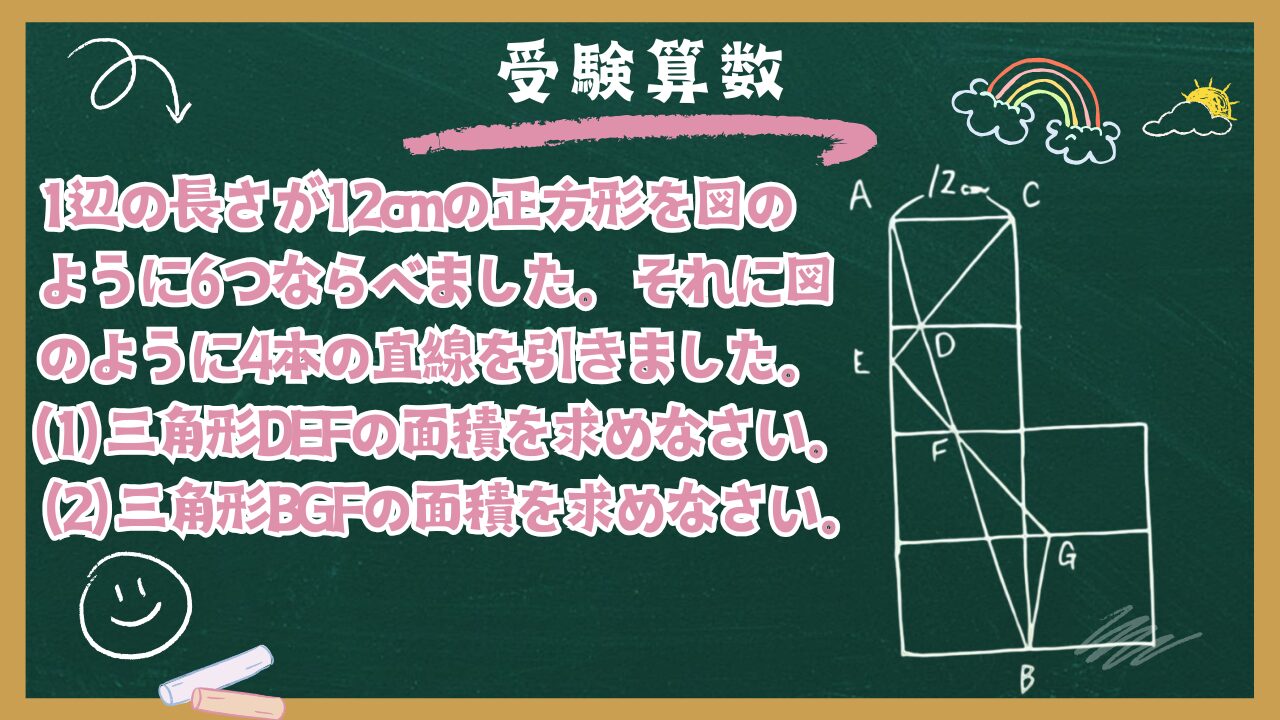
【受験算数】拡大・縮小：⑧正方形で作る図形
単元：
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
受験算数の森
問題文全文(内容文)：
大問1
1辺の長さが12cmの正方形を図のように6つならべました。それに図のように4本の直線を引きました。このとき次の問いに答えなさい。
(1) 三角形DEFの面積を求めなさい。
(2) 三角形BGFの面積を求めなさい。
大問2
1辺の長さが12cmの正方形を図のように6つならべました。それに図のように5本の直線を引きました。このとき次の問いに答えなさい。
(1) 三角形DEFの面積を求めなさい。
(2) 三角形BGFの面積を求めなさい。
この動画を見る
大問1
1辺の長さが12cmの正方形を図のように6つならべました。それに図のように4本の直線を引きました。このとき次の問いに答えなさい。
(1) 三角形DEFの面積を求めなさい。
(2) 三角形BGFの面積を求めなさい。
大問2
1辺の長さが12cmの正方形を図のように6つならべました。それに図のように5本の直線を引きました。このとき次の問いに答えなさい。
(1) 三角形DEFの面積を求めなさい。
(2) 三角形BGFの面積を求めなさい。
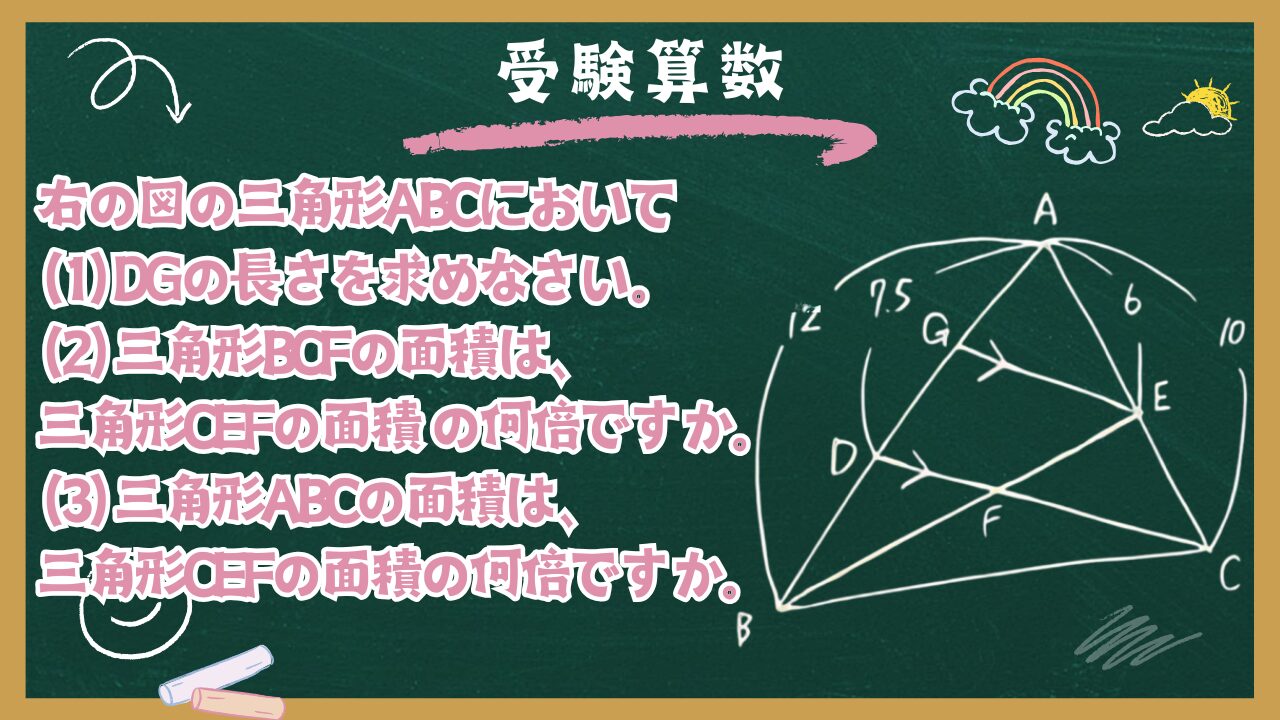
【受験算数】拡大・縮小：⑦平行線と相似4
単元：
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
受験算数の森
問題文全文(内容文)：
大問1
右の図の三角形ABCにおいて、AB=12cm, AC=10cmです。AB、AC上に点D、Eをそれぞれ AD=7.5cm、AE=6cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、 BEとCDの交点をFとします。次の問いに答えなさい。
(1) DGの長さを求めなさい。
(2) 三角形BCFの面積は、三角形CEFの面積 の何倍ですか。
(3) 三角形ABCの面積は、三角形CEFの面積の何倍ですか。
大問2
右の図の三角形ABCにおいて、AB=10cm, AC=8です。AB、AC上に点D、Eをそれぞれ AD=6.4cm、 AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、 BEとCDの交点をFとします。次の問いに答えなさい。
(1) DGの長さを求めなさい。
(2) 三角形BCFの面積は、三角形CEFの面積 の何倍ですか。
(3) 三角形ABCの面積は、三角形CEFの面積の何倍ですか。
この動画を見る
大問1
右の図の三角形ABCにおいて、AB=12cm, AC=10cmです。AB、AC上に点D、Eをそれぞれ AD=7.5cm、AE=6cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、 BEとCDの交点をFとします。次の問いに答えなさい。
(1) DGの長さを求めなさい。
(2) 三角形BCFの面積は、三角形CEFの面積 の何倍ですか。
(3) 三角形ABCの面積は、三角形CEFの面積の何倍ですか。
大問2
右の図の三角形ABCにおいて、AB=10cm, AC=8です。AB、AC上に点D、Eをそれぞれ AD=6.4cm、 AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、 BEとCDの交点をFとします。次の問いに答えなさい。
(1) DGの長さを求めなさい。
(2) 三角形BCFの面積は、三角形CEFの面積 の何倍ですか。
(3) 三角形ABCの面積は、三角形CEFの面積の何倍ですか。
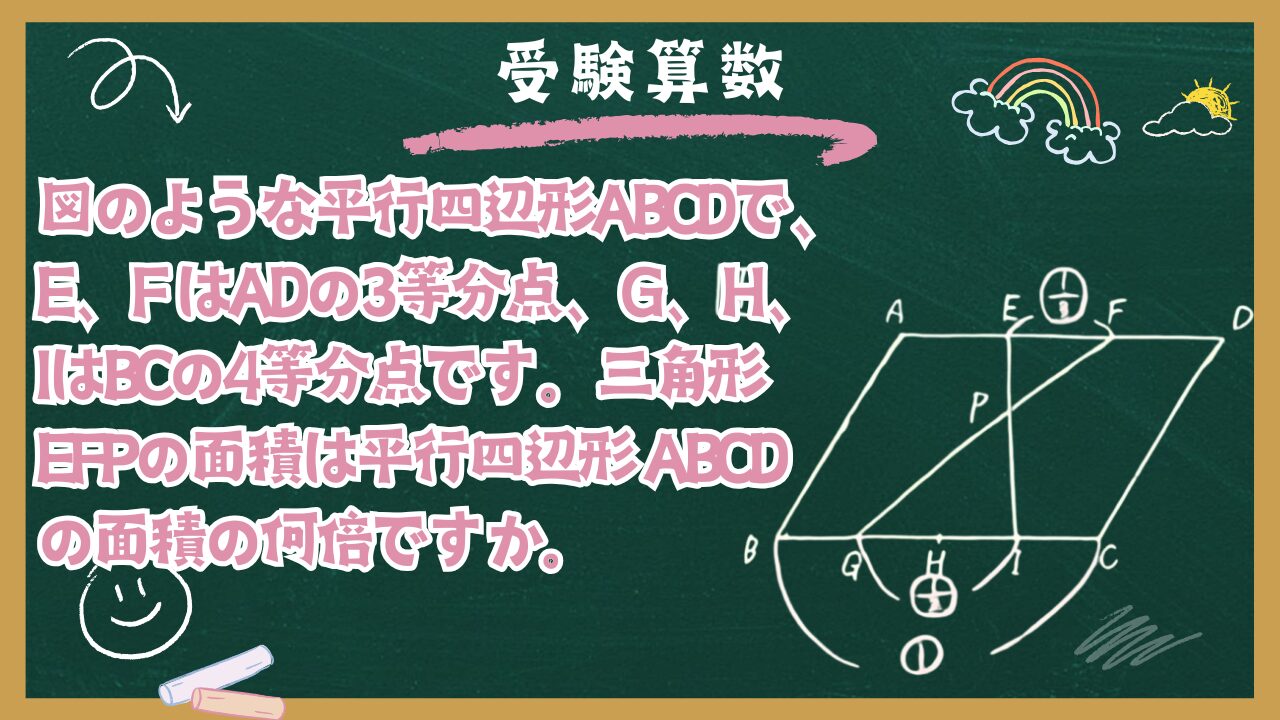
【受験算数】拡大・縮小：⑦平行線と相似3
単元：
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
受験算数の森
問題文全文(内容文)：
大問1
図のような平行四辺形ABCDで、E、F はADの3等分点、G、H、IはBCの4等分点です。三角形EFPの面積は平行四辺形 ABCDの面積の何倍ですか。
大問2
図のような平行四辺形ABCDで、E、F、GはADの4等分点、H、I、J、KはBCの5等分点です。三角形PEGの面積は平行四辺形ABCDの面積の何倍ですか。
この動画を見る
大問1
図のような平行四辺形ABCDで、E、F はADの3等分点、G、H、IはBCの4等分点です。三角形EFPの面積は平行四辺形 ABCDの面積の何倍ですか。
大問2
図のような平行四辺形ABCDで、E、F、GはADの4等分点、H、I、J、KはBCの5等分点です。三角形PEGの面積は平行四辺形ABCDの面積の何倍ですか。
【受験算数】小数・分数：⑧大きさ比べ
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他#約数・倍数を利用する問題
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
受験算数の森
問題文全文(内容文)：
大問1
分数を小数で表し、小数第3位を四捨五入したとき、0.04となるものはたくさんあります。そのうちで分子が1となるものを考えるとき、最も小さな分数は(1/A)で、 最も大きいものは(1/B)です。
また、分母と分子の和が450となる既約分数(約分できない分数)はCとDです。A、B、C、Dにあてはまる数を書きなさい。
大問2
分数を小数で表し、小数第3位を四捨五入したとき、0.03となるものはたくさんあります。そのうちで分子が1となるものを考えるとき、最も小さな分数は(1/A)で、 最も大きいものは(1/B)です。
また、分母と分子の和が56となる既約分数(約分できない分数)はCとDとEです。 A、B、C、D、Eにあてはまる数を書きなさい。
この動画を見る
大問1
分数を小数で表し、小数第3位を四捨五入したとき、0.04となるものはたくさんあります。そのうちで分子が1となるものを考えるとき、最も小さな分数は(1/A)で、 最も大きいものは(1/B)です。
また、分母と分子の和が450となる既約分数(約分できない分数)はCとDです。A、B、C、Dにあてはまる数を書きなさい。
大問2
分数を小数で表し、小数第3位を四捨五入したとき、0.03となるものはたくさんあります。そのうちで分子が1となるものを考えるとき、最も小さな分数は(1/A)で、 最も大きいものは(1/B)です。
また、分母と分子の和が56となる既約分数(約分できない分数)はCとDとEです。 A、B、C、D、Eにあてはまる数を書きなさい。
【受験算数】小数・分数：⑧単位分数の和
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
受験算数の森
問題文全文(内容文)：
大問1
今から何千年も前のエジプトの人々が、分数を分母の異なる単位分数の和で表した記録がたくさん発見されています。(単位分数とは$\displaystyle \frac{1}{2}、\frac{1}{3}、\frac{1}{4}…$のように分子が1の分数をいいます。)
$\displaystyle \frac{4}{5}=\frac{1}{2}+\frac{1}{4}+\frac{1}{20} \frac{3}{8}=\frac{1}{3}+\frac{1}{24} \frac{8}{9}=\frac{1}{2}+\frac{1}{3}+\frac{1}{18}$ のようなものです。
このような表し方として、次のような方法が考えられます。たとえば$\displaystyle \frac{4}{5}$について 考えると、$\displaystyle \frac{4}{5}$は$\displaystyle \frac{1}{2}$より大きいのでまず$\displaystyle \frac{1}{2}$をとると、$\displaystyle \frac{4}{5}-\frac{1}{2}=\frac{3}{10}、\frac{3}{10}$から$\displaystyle \frac{1}{3}$はとれないので$\displaystyle \frac{1}{4}$をとると、$\displaystyle \frac{3}{10}-\frac{1}{4}=\frac{1}{20}$、したがって$\displaystyle \frac{4}{5}=\frac{1}{2}+\frac{1}{4}+\frac{1}{20}$と
できます。
この方法で次の分数を単位分数の和で表しなさい。
(1) $\displaystyle \frac{3}{4}$
(2) $\displaystyle \frac{4}{7}$
(3) $\displaystyle \frac{11}{35}$
大問2
この方法で次の分数を単位分数の和で表しなさい。
(1) $\displaystyle \frac{2}{7}$
(2) $\displaystyle \frac{11}{12}$
(3) $\displaystyle \frac{5}{13}$
この動画を見る
大問1
今から何千年も前のエジプトの人々が、分数を分母の異なる単位分数の和で表した記録がたくさん発見されています。(単位分数とは$\displaystyle \frac{1}{2}、\frac{1}{3}、\frac{1}{4}…$のように分子が1の分数をいいます。)
$\displaystyle \frac{4}{5}=\frac{1}{2}+\frac{1}{4}+\frac{1}{20} \frac{3}{8}=\frac{1}{3}+\frac{1}{24} \frac{8}{9}=\frac{1}{2}+\frac{1}{3}+\frac{1}{18}$ のようなものです。
このような表し方として、次のような方法が考えられます。たとえば$\displaystyle \frac{4}{5}$について 考えると、$\displaystyle \frac{4}{5}$は$\displaystyle \frac{1}{2}$より大きいのでまず$\displaystyle \frac{1}{2}$をとると、$\displaystyle \frac{4}{5}-\frac{1}{2}=\frac{3}{10}、\frac{3}{10}$から$\displaystyle \frac{1}{3}$はとれないので$\displaystyle \frac{1}{4}$をとると、$\displaystyle \frac{3}{10}-\frac{1}{4}=\frac{1}{20}$、したがって$\displaystyle \frac{4}{5}=\frac{1}{2}+\frac{1}{4}+\frac{1}{20}$と
できます。
この方法で次の分数を単位分数の和で表しなさい。
(1) $\displaystyle \frac{3}{4}$
(2) $\displaystyle \frac{4}{7}$
(3) $\displaystyle \frac{11}{35}$
大問2
この方法で次の分数を単位分数の和で表しなさい。
(1) $\displaystyle \frac{2}{7}$
(2) $\displaystyle \frac{11}{12}$
(3) $\displaystyle \frac{5}{13}$
【受験算数】小数・分数：⑦循環小数応用
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
受験算数の森
問題文全文(内容文)：
大問1
$\displaystyle \frac{1}{9}=(1÷9)=0.1111…、\frac{1}{99}=(1÷99)=0.010101…、\frac{1}{999} =(1÷999)=0.001001001…$です。次の問いに答えなさい。
(1) 次の小数を分数で表しなさい。
① 0.36363636…
② 0.040740740740…
③ 0.481818181
(2) 次の計算の結果を小数で表しなさい。
① $\displaystyle \frac{1}{9}+\frac{23}{99}$
② $\displaystyle \frac{2}{90}+\frac{34}{99}$
(3)$\displaystyle \frac{150}{1111}$を小数て表したとき、小数第30位の数は何ですか。
大問2
$\displaystyle \frac{1}{9}=(1÷9)=0.1111…、\frac{1}{99}=(1÷99)=0.010101…、\frac{1}{999} =(1÷999)=0.001001001…$です。次の問いに答えなさい。
(1) 次の小数を分数で表しなさい。
① 0.25252525…
② 0.518518518…
③ 0.216161616…
(2) 次の計算の結果を小数で表しなさい。
① $\displaystyle \frac{2}{9}+\frac{35}{99}$
② $\displaystyle \frac{5}{90}+\frac{21}{999}$
(3) $\displaystyle \frac{13}{37}$を小数で表したとき、小数第二位の数は何ですか。
この動画を見る
大問1
$\displaystyle \frac{1}{9}=(1÷9)=0.1111…、\frac{1}{99}=(1÷99)=0.010101…、\frac{1}{999} =(1÷999)=0.001001001…$です。次の問いに答えなさい。
(1) 次の小数を分数で表しなさい。
① 0.36363636…
② 0.040740740740…
③ 0.481818181
(2) 次の計算の結果を小数で表しなさい。
① $\displaystyle \frac{1}{9}+\frac{23}{99}$
② $\displaystyle \frac{2}{90}+\frac{34}{99}$
(3)$\displaystyle \frac{150}{1111}$を小数て表したとき、小数第30位の数は何ですか。
大問2
$\displaystyle \frac{1}{9}=(1÷9)=0.1111…、\frac{1}{99}=(1÷99)=0.010101…、\frac{1}{999} =(1÷999)=0.001001001…$です。次の問いに答えなさい。
(1) 次の小数を分数で表しなさい。
① 0.25252525…
② 0.518518518…
③ 0.216161616…
(2) 次の計算の結果を小数で表しなさい。
① $\displaystyle \frac{2}{9}+\frac{35}{99}$
② $\displaystyle \frac{5}{90}+\frac{21}{999}$
(3) $\displaystyle \frac{13}{37}$を小数で表したとき、小数第二位の数は何ですか。
【受験算数】速さに関する問題(D2)：平均の速さ2
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#5年算数D-支援#中学受験教材#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
A地とB地の間を、行きは時速30km、帰りは時速□kmで往復すると、往復の平均の速さは時速36kmになります。
この動画を見る
A地とB地の間を、行きは時速30km、帰りは時速□kmで往復すると、往復の平均の速さは時速36kmになります。
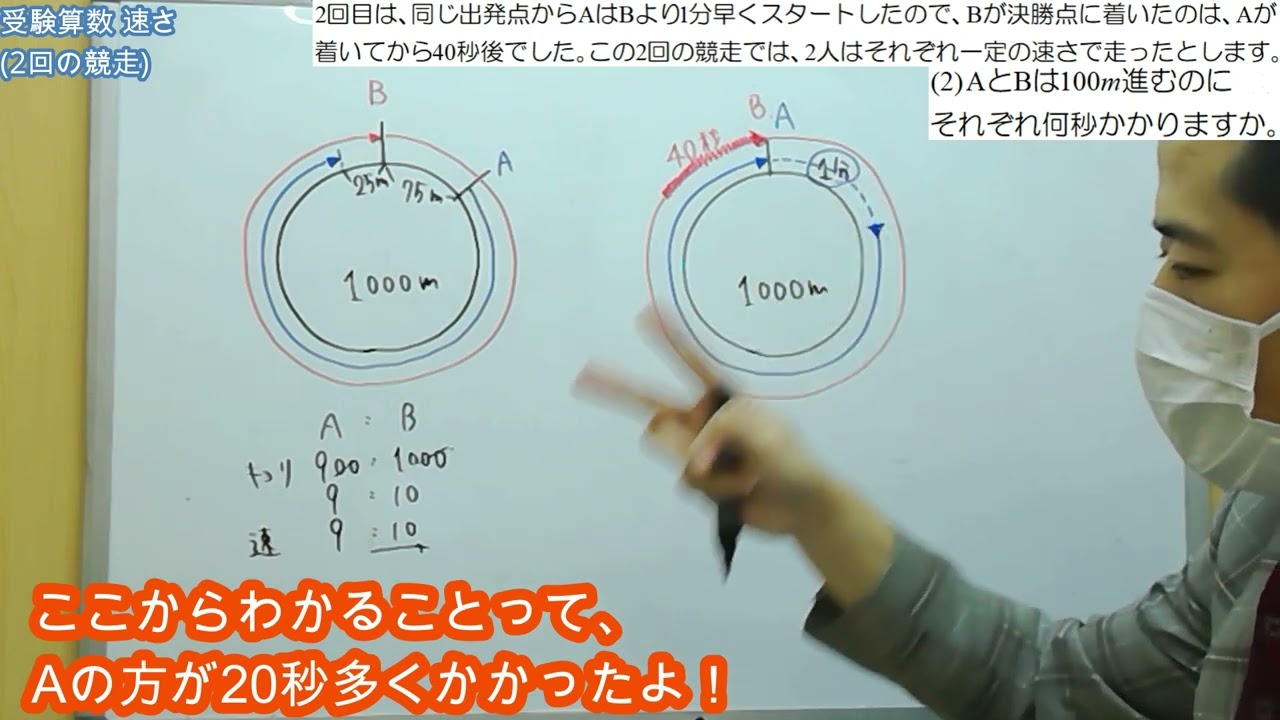
【受験算数】速さに関する問題(D1)：2回の競走
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#5年算数D-支援#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
A、B2人が1000mある池の周囲を一周する競走を2回おこないました。1回目は、AはBより75mだけ出発点を先に進め、Bの出発点を決勝点として同時にスタートしましたが、Bが決勝点に着いたときにはAはまだ25m残していました。2回目は、同じ出発点からAはBより1分早くスタートしたので、Bが決勝点に着いたのは、Aが着いてから40秒後でした。この2回の競走では、2人はそれぞれ一定の速さで走ったとします。次の問いに答えなさい。
(1)AとBの速さの比を求めなさい。
(2)AとBは100m進むのにそれぞれ何秒かかりますか。
この動画を見る
A、B2人が1000mある池の周囲を一周する競走を2回おこないました。1回目は、AはBより75mだけ出発点を先に進め、Bの出発点を決勝点として同時にスタートしましたが、Bが決勝点に着いたときにはAはまだ25m残していました。2回目は、同じ出発点からAはBより1分早くスタートしたので、Bが決勝点に着いたのは、Aが着いてから40秒後でした。この2回の競走では、2人はそれぞれ一定の速さで走ったとします。次の問いに答えなさい。
(1)AとBの速さの比を求めなさい。
(2)AとBは100m進むのにそれぞれ何秒かかりますか。
【受験算数】速さに関する問題(C4)：途中で出会う
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#5年算数D-支援#中学受験教材#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
大川君はA地からB地に向かって、小山君はB地からA地に向かって、同時に歩き始めました。2人は歩き始めてから28分後にP地点で出会いました。大川君は出会ってから20分後にB地に着きました。そのとき、小山君はA地の手前960mのところを歩いていました。
(1)大川君と小山君の速さの比は何対何ですか。
(2)A地とB地は何m離れていますか。
(3)P地点はA地から何mのところですか。
この動画を見る
大川君はA地からB地に向かって、小山君はB地からA地に向かって、同時に歩き始めました。2人は歩き始めてから28分後にP地点で出会いました。大川君は出会ってから20分後にB地に着きました。そのとき、小山君はA地の手前960mのところを歩いていました。
(1)大川君と小山君の速さの比は何対何ですか。
(2)A地とB地は何m離れていますか。
(3)P地点はA地から何mのところですか。
【受験算数】速さに関する問題(C3)：バス停まで歩く
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#5年算数D-支援#中学受験教材#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
太郎くんは家からバス停まで歩き、7分待ったあとバスに乗って駅に着きました。家を出てから駅に着くまでにかかった時間は23分でした。帰りは駅から行きと同じ道を歩いて65分で家に着きました。バスの速さは分速550m、歩く速さは時速3.6kmとします。
(1)家から駅までの道のりは何mですか。
(2)家からバス停までの道のりは何mですか。
この動画を見る
太郎くんは家からバス停まで歩き、7分待ったあとバスに乗って駅に着きました。家を出てから駅に着くまでにかかった時間は23分でした。帰りは駅から行きと同じ道を歩いて65分で家に着きました。バスの速さは分速550m、歩く速さは時速3.6kmとします。
(1)家から駅までの道のりは何mですか。
(2)家からバス停までの道のりは何mですか。
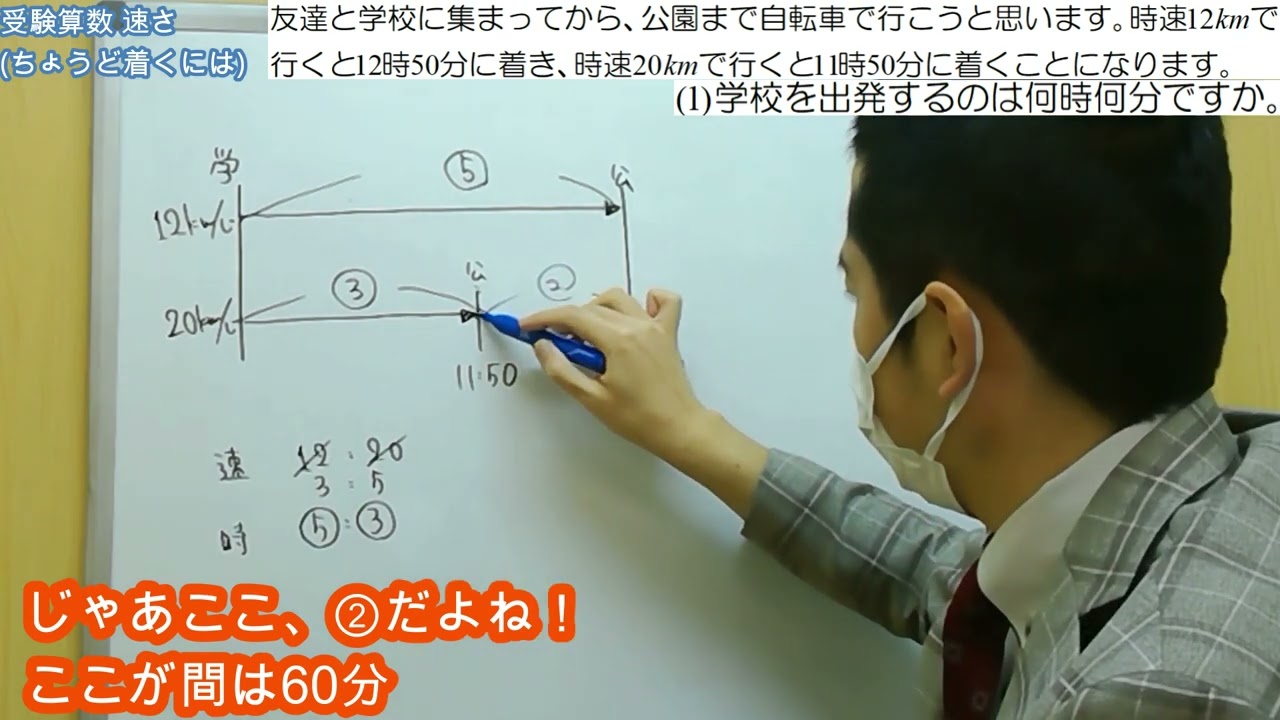
【受験算数】速さに関する問題(C2)：ちょうど着くには
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#5年算数D-支援#中学受験教材#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
友達と学校に集まってから、公園まで自転車で行こうと思います。時速12kmで行くと12時50分に着き、時速20kmで行くと11時50分に着くことになります。
(1)学校を出発するのは何時何分ですか。
(2)学校から公園までの距離は何kmですか。
(3)ちょうど12時に着くようにするには、時速何kmで行けばよいですか。
この動画を見る
友達と学校に集まってから、公園まで自転車で行こうと思います。時速12kmで行くと12時50分に着き、時速20kmで行くと11時50分に着くことになります。
(1)学校を出発するのは何時何分ですか。
(2)学校から公園までの距離は何kmですか。
(3)ちょうど12時に着くようにするには、時速何kmで行けばよいですか。
【SPX小5算数51-F04】速さに関する問題(C1)：引き返す【SPX W-支援】
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#中学受験教材#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
P地とQ地は1km離れています。太郎くんが毎分90mの速さで、次郎くんが毎分70mの速さで同時にP地を出発してQ地に向かいました。太郎くんがQ地に着いてすぐに引き返すと、次郎くんと出会うのはP地から何m離れた地点ですか。
この動画を見る
P地とQ地は1km離れています。太郎くんが毎分90mの速さで、次郎くんが毎分70mの速さで同時にP地を出発してQ地に向かいました。太郎くんがQ地に着いてすぐに引き返すと、次郎くんと出会うのはP地から何m離れた地点ですか。
【SPX小5算数51-F04】速さに関する問題(B4)：平均の速さ【SPX W-支援】
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#中学受験教材#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
A地とB地の間を、行きは時速7km、帰りは時速5kmで往復しました。この時、往復の平均の速さは時速何kmですか。
この動画を見る
A地とB地の間を、行きは時速7km、帰りは時速5kmで往復しました。この時、往復の平均の速さは時速何kmですか。
【SPX小5算数51-F04】速さに関する問題(B3)：池の周りを回る: 和差算の利用【SPX W-支援】
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#中学受験教材#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
池の周囲を1周する道があります。A君とB君が同時に同じところを出発して同じ方向に回ると、70分後にA君はB君にはじめて追いつき、同時に同じところを出発して反対方向に回ると、30分後に2人ははじめて出会いました。A君、B君がこの道を1周するのにかかる時間はそれぞれ何分ですか 。
この動画を見る
池の周囲を1周する道があります。A君とB君が同時に同じところを出発して同じ方向に回ると、70分後にA君はB君にはじめて追いつき、同時に同じところを出発して反対方向に回ると、30分後に2人ははじめて出会いました。A君、B君がこの道を1周するのにかかる時間はそれぞれ何分ですか 。
【SPX小5算数51-F04】速さに関する問題(B2)：往復する 【SPX W-支援】
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#中学受験教材#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
太郎くんはA地とB地の間を自転車で往復しました。行きは時速12kmで、帰りは時速20kmで走ったら、全部で4時間かかりました。
(1)行きは何時間何分かかりましたか。
(2)A地とB地の間の距離は何kmですか。
この動画を見る
太郎くんはA地とB地の間を自転車で往復しました。行きは時速12kmで、帰りは時速20kmで走ったら、全部で4時間かかりました。
(1)行きは何時間何分かかりましたか。
(2)A地とB地の間の距離は何kmですか。
【SPX小5算数51-F04】速さに関する問題(B1)：引き返す 【SPX W-支援】
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#中学受験教材#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
A地点とB地点は1200m離れています。太郎くんと次郎くんが同時にA地点を出発してB地点に向かいました。太郎くんがB地点に着いてすぐ引き返すと、B地点から200m離れたところで次郎くんと出会いました。太郎くんと次郎くんの速さの比をもっとも簡単な整数の比で求めなさい。
この動画を見る
A地点とB地点は1200m離れています。太郎くんと次郎くんが同時にA地点を出発してB地点に向かいました。太郎くんがB地点に着いてすぐ引き返すと、B地点から200m離れたところで次郎くんと出会いました。太郎くんと次郎くんの速さの比をもっとも簡単な整数の比で求めなさい。
【予習シリーズ算数・小6上】部活の人数比から総人数【割合と比の文章題】
単元：
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
教材：
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師：
受験算数の森
問題文全文(内容文)：
ある中学の生徒数について、次のことが分かっています。
・男子と女子の人数の比は6:5
・部活動をしている人については、男子と女子の人数の比は8:7
・部活動をしていない人については、男子と女子の人数の比は4:3
・部活動をしている人は、男女合わせて300人
この中学校の生徒数は全部で何人ですか。
この動画を見る
ある中学の生徒数について、次のことが分かっています。
・男子と女子の人数の比は6:5
・部活動をしている人については、男子と女子の人数の比は8:7
・部活動をしていない人については、男子と女子の人数の比は4:3
・部活動をしている人は、男女合わせて300人
この中学校の生徒数は全部で何人ですか。
【予習シリーズ算数・小6上】売買損益と線分図【割合と比の文章題】
単元：
#算数(中学受験)#文章題#売買損益と食塩水
教材：
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師：
受験算数の森
問題文全文(内容文)：
ある品物を□円で仕入れ、仕入れ値の2割の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の１割引きにしたところ、品物は売れて利益は１６０円になりました。
この動画を見る
ある品物を□円で仕入れ、仕入れ値の2割の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の１割引きにしたところ、品物は売れて利益は１６０円になりました。
【SPX小5算数51-F04】速さに関する問題(A4)：途中で速さが変わる 【SPX W-支援】
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#中学受験教材#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
A地点からB地点を通ってC地点まで3.3kmの道があります。花子さんは、A地点からB地点まで分速60m、B地点からC地点まで分速75mで歩いたところ52分かかりました。A地点からB地点までの距離は何mですか。
この動画を見る
A地点からB地点を通ってC地点まで3.3kmの道があります。花子さんは、A地点からB地点まで分速60m、B地点からC地点まで分速75mで歩いたところ52分かかりました。A地点からB地点までの距離は何mですか。
【SPX小5算数51-F04】速さに関する問題(A3)：池の周りを回る 【SPX W-支援】
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#中学受験教材
指導講師：
受験算数の森
問題文全文(内容文)：
池の周囲を一周する道があります。この道を一周するのにAは24分、Bは40分かかります。
(1)２人が同時に同じところを出発して反対の方向に進むと、何分後にはじめて出会いますか。
(2)２人が同時に同じところを出発して同じ方向に進むと、AがBにはじめて追いつくのは何分後ですか。
この動画を見る
池の周囲を一周する道があります。この道を一周するのにAは24分、Bは40分かかります。
(1)２人が同時に同じところを出発して反対の方向に進むと、何分後にはじめて出会いますか。
(2)２人が同時に同じところを出発して同じ方向に進むと、AがBにはじめて追いつくのは何分後ですか。
【SPX小5算数51-F04】速さに関する問題(A2)：同時に着く 【SPX W-支援】
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#中学受験教材#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
Aさんは家から学校まで徒歩で、Bさんは家から学校まで自転車で通っています。Aさんの時速は3.6km、Bさんの時速は16.2㎞です。今日、二人は同じ時刻にそれぞれの家を出発し、同時に学校につきました。Aさんの家から学校までは800mです。Bさんの家から学校までは何mですか。
この動画を見る
Aさんは家から学校まで徒歩で、Bさんは家から学校まで自転車で通っています。Aさんの時速は3.6km、Bさんの時速は16.2㎞です。今日、二人は同じ時刻にそれぞれの家を出発し、同時に学校につきました。Aさんの家から学校までは800mです。Bさんの家から学校までは何mですか。
【SPX小5算数51-F04】速さに関する問題(A1)：学校に行く 【SPX W-支援】
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#中学受験教材#5年算数W-支援
指導講師：
受験算数の森
問題文全文(内容文)：
兄と弟は同時に家を出発して、家から1800m離れた学校までそれぞれ一定の速さで進みました。兄が学校についたとき、弟は学校まであと300mのところにいました。兄と弟の速さの比は何対何ですか。
この動画を見る
兄と弟は同時に家を出発して、家から1800m離れた学校までそれぞれ一定の速さで進みました。兄が学校についたとき、弟は学校まであと300mのところにいました。兄と弟の速さの比は何対何ですか。
【SPX小5算数51-24】仕事算(D4)：クラスで稲刈り【D-支援確認編】
単元：
#算数(中学受験)#文章題#仕事算とニュートン算
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
受験算数の森
問題文全文(内容文)：
あるクラスで水田Aと水田Bの稲刈りをしました。水田Aは水田Bの2倍の広さです。初めの1時間は全員で水田Aの稲刈りをし、次の1時間は、クラスを半分ずつに分けて、一方が水田A、もう一方が水田Bの稲刈りをしました。その結果、水田Aはちょうど刈り終えましたが、水田Bの方は終わらなかったので、何人か残って稲刈りをしたところ、さらに40分かかりました。次の問いに答えなさい。
(1)初めの1時間で刈ったのは、水田A全体の何分のいくつですか。
(2)最後の40分で刈ったところを、全員で刈っていたら何分かかりますか。
(3)クラスの人数は何人ですか。ただし、このクラスは25人以上35人以下です。
この動画を見る
あるクラスで水田Aと水田Bの稲刈りをしました。水田Aは水田Bの2倍の広さです。初めの1時間は全員で水田Aの稲刈りをし、次の1時間は、クラスを半分ずつに分けて、一方が水田A、もう一方が水田Bの稲刈りをしました。その結果、水田Aはちょうど刈り終えましたが、水田Bの方は終わらなかったので、何人か残って稲刈りをしたところ、さらに40分かかりました。次の問いに答えなさい。
(1)初めの1時間で刈ったのは、水田A全体の何分のいくつですか。
(2)最後の40分で刈ったところを、全員で刈っていたら何分かかりますか。
(3)クラスの人数は何人ですか。ただし、このクラスは25人以上35人以下です。
【SPX小5算数51-24】仕事算(D3)：2人ずつの仕事算【D-支援確認編】
単元：
#算数(中学受験)#文章題#仕事算とニュートン算
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
受験算数の森
問題文全文(内容文)：
ある仕事をするのに、AとB2人では48日、BとC2人では40日、CとA2人では60日かかります。この仕事をA1人ですると何日かかりますか。
この動画を見る
ある仕事をするのに、AとB2人では48日、BとC2人では40日、CとA2人では60日かかります。この仕事をA1人ですると何日かかりますか。
【SPX小5算数51-24】仕事算(D2)：仕事算(応用)【D-支援確認編】
単元：
#算数(中学受験)#文章題#仕事算とニュートン算
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
受験算数の森
問題文全文(内容文)：
AとBとCの3人で働けば16日で終わる仕事があります。もし、Cが4日休めば、その分をAとBの2人が1日多く働くか、またはB1人が5日多く働かなければ、この仕事は終わりません。
(1)Cが1人でこの仕事を終わらせるには、何日働けばよいですか。
(2)Aが1人でこの仕事を終わらせるには、何日働けばよいですか。
この動画を見る
AとBとCの3人で働けば16日で終わる仕事があります。もし、Cが4日休めば、その分をAとBの2人が1日多く働くか、またはB1人が5日多く働かなければ、この仕事は終わりません。
(1)Cが1人でこの仕事を終わらせるには、何日働けばよいですか。
(2)Aが1人でこの仕事を終わらせるには、何日働けばよいですか。
【SPX小5算数51-24】仕事算(D1)：大人と子ども【D-支援確認編】
単元：
#算数(中学受験)#文章題#仕事算とニュートン算
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
受験算数の森
問題文全文(内容文)：
ある仕事をするのに、大人3人ですると終わるまでに10日かかり、子ども5人ですると終わるまでに9日かかります。
(1)大人1人と子ども1人の1日あたりの仕事量の比を、最も簡単な整数の比で答えなさい。
(2)この仕事を、大人4人と子ども3人で同時にすると、終わるまでに何日かかりますか。
この動画を見る
ある仕事をするのに、大人3人ですると終わるまでに10日かかり、子ども5人ですると終わるまでに9日かかります。
(1)大人1人と子ども1人の1日あたりの仕事量の比を、最も簡単な整数の比で答えなさい。
(2)この仕事を、大人4人と子ども3人で同時にすると、終わるまでに何日かかりますか。
【SPX小5算数51-24】仕事算(C4)：2本の管を使う【D-支援確認編】
単元：
#算数(中学受験)#文章題#仕事算とニュートン算
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
受験算数の森
問題文全文(内容文)：
ある水そうに水を入れるのに、A管で16分入れた後、B管で3分入れると満水になります。また、A管で4分入れた後、B管で17分入れても満水になります。
(1)A管とB管から1分間に入れることができる水の量の比を、最も簡単な整数の比で答えなさい。
(2)はじめからA管とB管の2本の管を使って水を入れると、何分で満水になりますか。
この動画を見る
ある水そうに水を入れるのに、A管で16分入れた後、B管で3分入れると満水になります。また、A管で4分入れた後、B管で17分入れても満水になります。
(1)A管とB管から1分間に入れることができる水の量の比を、最も簡単な整数の比で答えなさい。
(2)はじめからA管とB管の2本の管を使って水を入れると、何分で満水になりますか。