推理と論証
推理と論証
福田のおもしろ数学185〜8枚の硬貨から1枚の偽物を天秤を使って見抜こう
単元：
#算数(中学受験)#推理と論証#推理と論証
指導講師：
福田次郎
問題文全文(内容文)：
8枚の区別のつかない硬貨のなかに、本物よりも軽い偽物が1枚混じっている。
おもりなしの天秤を使って偽物を見つけ出すためには、最小で南海天秤を使えばよいでしょうか。
この動画を見る
8枚の区別のつかない硬貨のなかに、本物よりも軽い偽物が1枚混じっている。
おもりなしの天秤を使って偽物を見つけ出すためには、最小で南海天秤を使えばよいでしょうか。
予習シリーズ算数６年上P188「練習問題」①
単元：
#算数(中学受験)#推理と論証#推理と論証
教材：
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師：
重吉
問題文全文(内容文)：
生徒5人Aさん、Bさん、Cさん、Dさん、Eさんの発言を基に、それぞれ学年と性別を求めよ
【発言内容】
・Bさんは5年生です
・Cさんは学年が違い、性別も違います
・5年生は3人います、そのうち女子は1人、男子は2人います
・6年生は2人います
・Aさんは女性です
・AさんとDさんは同学年です
この動画を見る
生徒5人Aさん、Bさん、Cさん、Dさん、Eさんの発言を基に、それぞれ学年と性別を求めよ
【発言内容】
・Bさんは5年生です
・Cさんは学年が違い、性別も違います
・5年生は3人います、そのうち女子は1人、男子は2人います
・6年生は2人います
・Aさんは女性です
・AさんとDさんは同学年です
予習シリーズ算数6年上P184「ステップアップ演習」①
単元：
#算数(中学受験)#推理と論証#推理と論証
指導講師：
重吉
問題文全文(内容文)：
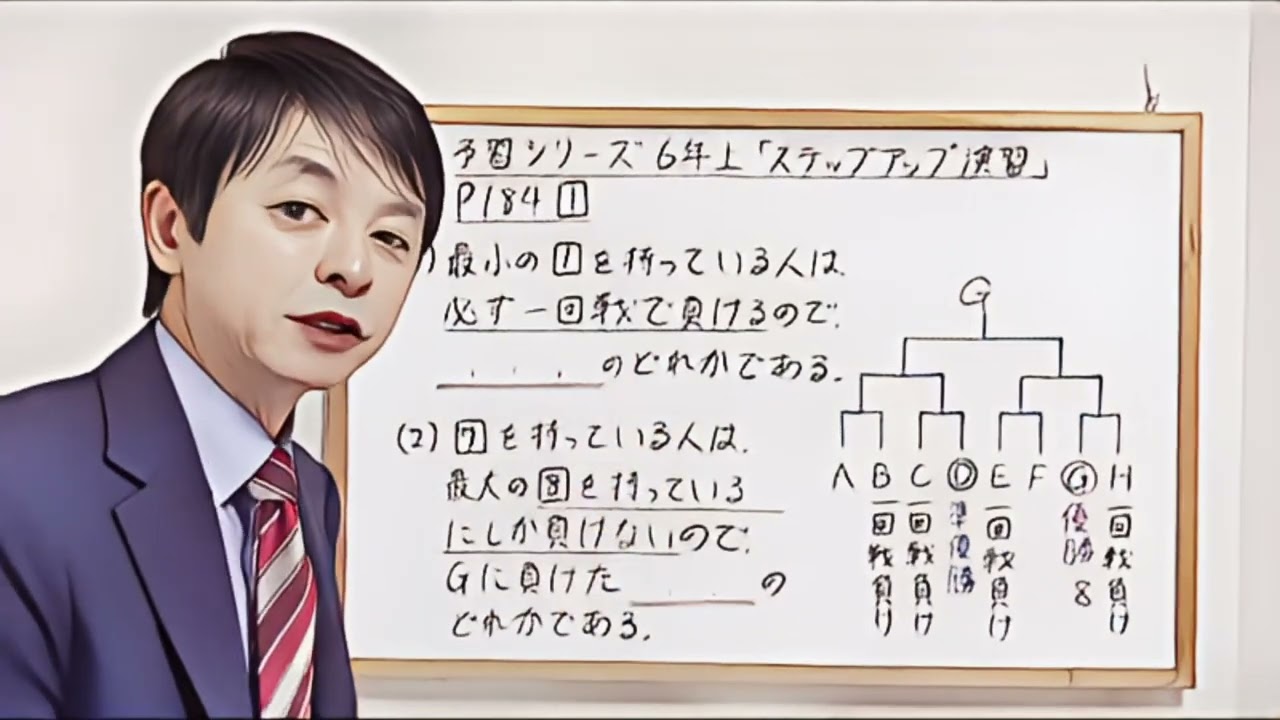
トーナメント票があり、AさんからHさんたちはそれぞれ、1～8の数字を持っています
大きい数字を持っている方が勝ちとなり、8人の中でGさんが優勝しました
AさんからHさんまでがそれぞなんの数字を持っていたか求めなさい
この動画を見る
トーナメント票があり、AさんからHさんたちはそれぞれ、1～8の数字を持っています
大きい数字を持っている方が勝ちとなり、8人の中でGさんが優勝しました
AさんからHさんまでがそれぞなんの数字を持っていたか求めなさい
福田の数学〜京都大学2023年理系第６問〜チェビシェフの多項式と論証(PART2)
単元：
#式の計算（単項式・多項式・式の四則計算）#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#その他#推理と論証#推理と論証#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{6}$ pを3以上の素数とする。また、θを実数とする。
(1)$\cos3\theta$と$\cos4\theta$を$\cos\theta$の式として表せ。
(2)$\cos\theta$=$\frac{1}{p}$のとき、θ=$\frac{m}{n}$・$\pi$となるような正の整数m,nが存在するか否かを理由をつけて判定せよ。
チェビシェフの多項式
$\cos n\theta$=$T_n$($\cos\theta$)を満たすn次の多項式$T_n(x)$が存在し、その係数はすべて整数であり、最高次の係数が$2^{n-1}$である。
これが、すべての自然数nについて成り立つことを数学的帰納法で証明せよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{6}$ pを3以上の素数とする。また、θを実数とする。
(1)$\cos3\theta$と$\cos4\theta$を$\cos\theta$の式として表せ。
(2)$\cos\theta$=$\frac{1}{p}$のとき、θ=$\frac{m}{n}$・$\pi$となるような正の整数m,nが存在するか否かを理由をつけて判定せよ。
チェビシェフの多項式
$\cos n\theta$=$T_n$($\cos\theta$)を満たすn次の多項式$T_n(x)$が存在し、その係数はすべて整数であり、最高次の係数が$2^{n-1}$である。
これが、すべての自然数nについて成り立つことを数学的帰納法で証明せよ。
2023京都大学理系過去問
福田の数学〜京都大学2023年理系第６問〜チェビシェフの多項式と論証(PART1)
単元：
#式の計算（単項式・多項式・式の四則計算）#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#その他#推理と論証#推理と論証#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{6}$ pを3以上の素数とする。また、θを実数とする。
(1)$\cos3\theta$と$\cos4\theta$を$\cos\theta$の式として表せ。
(2)$\cos\theta$=$\frac{1}{p}$のとき、θ=$\frac{m}{n}$・$\pi$となるような正の整数m,nが存在するか否かを理由をつけて判定せよ。
チェビシェフの多項式
$\cos n\theta$=$T_n$($\cos\theta$)を満たすn次の多項式$T_n(x)$が存在し、その係数はすべて整数であり、最高次の係数が$2^{n-1}$である。
これが、すべての自然数nについて成り立つことを数学的帰納法で証明せよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{6}$ pを3以上の素数とする。また、θを実数とする。
(1)$\cos3\theta$と$\cos4\theta$を$\cos\theta$の式として表せ。
(2)$\cos\theta$=$\frac{1}{p}$のとき、θ=$\frac{m}{n}$・$\pi$となるような正の整数m,nが存在するか否かを理由をつけて判定せよ。
チェビシェフの多項式
$\cos n\theta$=$T_n$($\cos\theta$)を満たすn次の多項式$T_n(x)$が存在し、その係数はすべて整数であり、最高次の係数が$2^{n-1}$である。
これが、すべての自然数nについて成り立つことを数学的帰納法で証明せよ。
2023京都大学理系過去問
福田の1.5倍速演習〜合格する重要問題010〜千葉大学2015年度理系数学第６問〜論証と剰余類
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#推理と論証#推理と論証#千葉大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
k,m,nを自然数とする。以下の問いに答えよ。
(1)$2^k$を7で割った余りが4であるとする。このとき、kを3で割った余りは
2であることを示せ。
(2)$4m+5n$が3で割り切れるとする。このとき、$2^{mn}$を7で割った余りは
4ではないことを示せ。
2015千葉大学理系過去問
この動画を見る
k,m,nを自然数とする。以下の問いに答えよ。
(1)$2^k$を7で割った余りが4であるとする。このとき、kを3で割った余りは
2であることを示せ。
(2)$4m+5n$が3で割り切れるとする。このとき、$2^{mn}$を7で割った余りは
4ではないことを示せ。
2015千葉大学理系過去問
福田の数学〜慶應義塾大学2022年看護医療学部第２問(3)〜平方数を３で割った余りに関する論証
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#集合と命題（集合・命題と条件・背理法）#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#推理と論証#推理と論証#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\large\boxed{2}}$(3)次の2つの命題を証明せよ。
$(\textrm{i})$整数nが3の倍数でないならば、$n^2$を3で割った時の余りは1である。
$(\textrm{ii})$3つの整数$x,y,z$が等式$x^2+y^2=z^2$を満たすならば、
xとyの少なくとも一方は3の倍数である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{2}}$(3)次の2つの命題を証明せよ。
$(\textrm{i})$整数nが3の倍数でないならば、$n^2$を3で割った時の余りは1である。
$(\textrm{ii})$3つの整数$x,y,z$が等式$x^2+y^2=z^2$を満たすならば、
xとyの少なくとも一方は3の倍数である。
2022慶應義塾大学看護医療学科過去問
福田の数学〜大阪大学2022年理系第２問〜三角関数と論証
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#推理と論証#推理と論証#大阪大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\alpha=\frac{2\pi}{7}$とする。以下の問いに答えよ。
(1)$\cos4\alpha=\cos3\alpha$であることを示せ。
(2)$f(x)=8x^3+4x^2-4x-1$とするとき、$f(\cos\alpha)=0$が成り立つことを示せ。
(3)$\cos\alpha$は無理数であることを示せ。
2022大阪大学理系過去問
この動画を見る
$\alpha=\frac{2\pi}{7}$とする。以下の問いに答えよ。
(1)$\cos4\alpha=\cos3\alpha$であることを示せ。
(2)$f(x)=8x^3+4x^2-4x-1$とするとき、$f(\cos\alpha)=0$が成り立つことを示せ。
(3)$\cos\alpha$は無理数であることを示せ。
2022大阪大学理系過去問
【中学受験算数】論理問題！ウソつきを探せ！ 【毎日１題！中学受験算数１２】
単元：
#算数(中学受験)#推理と論証#推理と論証
指導講師：
こばちゃん塾
問題文全文(内容文)：
A,B,Cの3人が競争をした後、3人に順位を聞いてみると次のように答えました。
A「C君が1着だった」、B「僕よりA君が速かった」、C「Bさんは3着だった」
この3人のうち、1人だけがうそを言っています。
A,B,Cを正しい順番で並べなさい。
この動画を見る
A,B,Cの3人が競争をした後、3人に順位を聞いてみると次のように答えました。
A「C君が1着だった」、B「僕よりA君が速かった」、C「Bさんは3着だった」
この3人のうち、1人だけがうそを言っています。
A,B,Cを正しい順番で並べなさい。
【中学受験算数】超簡単！みんな苦手な論理問題を一瞬で解く裏技！ 【毎日１題！中学受験算数１１】
単元：
#算数(中学受験)#推理と論証#推理と論証
指導講師：
こばちゃん塾
問題文全文(内容文)：
A,B,C,Dの4人が算数のテストを受け、得点の高い順に順位をつけました。Aは一番でも4番でもなく、BはDよりも得点が高く、Cは3番でした。4人を得点の高い順に答えなさい。
この動画を見る
A,B,C,Dの4人が算数のテストを受け、得点の高い順に順位をつけました。Aは一番でも4番でもなく、BはDよりも得点が高く、Cは3番でした。4人を得点の高い順に答えなさい。