 アルゴリズムの表し方とプログラムの設計
アルゴリズムの表し方とプログラムの設計
 アルゴリズムの表し方とプログラムの設計
アルゴリズムの表し方とプログラムの設計
【情報Ⅰ】サイコロゲームのプログラムを解説

単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計
指導講師:
理数個別チャンネル
問題文全文(内容文):
第3問 次の問い(問1~3)に答えよ。
問1
次の生徒(A)と生徒(B)の会話文を読み,空欄 ア・ウ に当てはまる数字を答えよ。また,空欄 イ・エ に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
A:昨日の放課後,友人Cとサイコロを使ったゲームで盛り上がったのですが,今から一緒にそのサイコロゲームをしませんか?
B:いいですね。どんなゲームなのかルールを教えてください。
A:参加プレイヤーは1つのサイコロを5回振ります。サイコロを振った際の出目(出目)が奇数(1,3,5)であれば2ポイントが得点に加算されます。サイコロの出目が偶数(2,4,6)であれば3ポイントが得点から減算されます。この作業を5回繰り返したときの最終的な得点が最も高い人の勝ちというシンプルなゲームです。
B:なるほど,シンプルなルールですね。
A:例えば,サイコロを2回振った際の出目が3,4の順である場合の得点は,奇数が1回,偶数が1回出ているので,得点は-1点となり,残り3回サイコロを振った出目が1,5,4の順に出た場合の最終的な得点は[ア]点となります。
B:得点の計算方法も理解できたので,2人で今から対決してみませんか?
A:いいですね。でも,サイコロを持っていないので,情報の授業で学習したプログラミングを使って,このゲームをパソコン上で動くようにしてみましょう。
B:そうですね。せっかく授業で学んだプログラミングの知識をここで発揮しましょう。まずは何から考えていけばよいと思いますか?
A:今回使用するサイコロの目を出力する必要があるため,関数のプログラムを作って,サイコロを再現する方法を考えましょう。以下は,乱数を使う場合の関数の説明です。
【関数の説明と例】
乱数(値)・・・0から引数として与えられた値までの範囲内で,ランダムな数値が生成され,その値が戻り値となる。
例:引数が3なら戻り値は0から3までの整数となる。
A:例えば,乱数(2)という関数を実行すると,[イ]が戻り値の候補となります。サイコロの出目は1から6なので,関数にも少し工夫が必要です。
B:サイコロの出目を再現できるようになったら,次はサイコロの出目が奇数か偶数かを判定するプログラムが必要ですね。
A:偶数か奇数かを判定する方法は,判定したい値を[ウ]で割った余りを調べるとよいですね。奇数の場合は[ウ]で割った余りが1,偶数の場合は[ウ]で割った余りが0になります。例えば,3は奇数であり,4は偶数であることが判定できます。
B:この判定を行うとると,プログラムの中で余りを計算する必要がありますが,どうしたらいいですか?
A:プログラムには色々な演算子(表1)があります。これらの演算子を利用して余りを求めることができますね。
表1 演算子の種類と使用例
| 種類 | 演算子 | 計算例 | 答え |
| 加算 | + | 1+2 | 3 |
| 減算 | - | 5-3 | 2 |
| 乗算 | × | 3×2 | 6 |
| 除算 | / | 8/2 | 4 |
| 余り | % | 7%2 | 1 |
B:例えば,2つの値を足す場合は+の演算子を使い,割り算を行う場合は[エ]の演算子を使えばいいですね。
A:その通りです。演算子を使い分けることで,さまざまな計算を行うことができます。
[イ]の解答群
⓪ 0,2 ① 1,2 ② 0,1,2 ③ 1,2,3
[エ]の解答群
⓪ + ① - ② × ③ / ④ %
問2 次の文章の空欄 オ~ケ に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
B: うーん,もう少しプログラムを作るうえでヒントが欲しいですね。全体的な流れがわかるといいのですが。
A: それでは簡単なフローチャートを考えてみましょう(図1)。サイコロゲームの流れは,サイコロを振り,出目が偶数か奇数かを判定して,得点を計算する,といった行動を5回繰り返していますね。
(図1 サイコロゲームのフローチャート)
始め
score = 0
5回繰り返す
サイコロを振る
└─ NO → scoreから3減算
└─ YES → scoreに2加算
(分岐の菱形の中:オ)
得点表示
終わり
B: フローチャートは処理の流れが可視化されて,わかりやすいですね。分岐には オ を入れればいいですね。
AさんとBさんは,これまでのヒントからプログラムを考えてみた(図2)。変数scoreには得点を求めるため初期値として0を,変数diceにはサイコロの目を求める関数を設定している。
(図2 サイコロゲームの得点を計算するプログラム)
(01) score = 0
(02) i を 1 から カ ながら繰り返す:
(03) dice = キ
(04) もし ク ならば:
(05) score = ケ + 2
(06) そうでなければ:
(07) score = ケ - 3
(08) 表示する(”得点:”, score)
オ の解答群
⓪ 出目が偶数 ① 出目が奇数 ② score が 0 ③ score が 1
カ の解答群
⓪ 5まで1ずつ増やし ① 6まで1ずつ増やし ② 5まで1ずつ減らし ③ 6まで1ずつ減らし
キ の解答群
⓪ 乱数(5) ① 乱数(6) ② 乱数(5) + 1 ③ 乱数(6) + 1
ク の解答群
⓪ dice % 2 == 0 ① dice % 2 == 1 ② score % 2 == 0 ③ score % 2 == 1
ケ の解答群
⓪ score ① dice ② i ③ i + 1
問3 次の文章を参考に,図3のプログラムの空欄【コ—シ】に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
A: プログラム(図2)が完成しました。これでサイコロゲームがコンピュータでも実行できるようになりました。
B: プログラムを動かしてみましょう。【2人でプログラムを実行してみた】
【実行結果】
Aさんの表示 得点:0
Bさんの表示 得点:5
A: きちんと動きました。Bさんの勝ちですね。もう少し白熱するようにゲームの要素を追加しませんか? 最後に特定の条件を満たした場合にボーナスポイントを与えるのはどうでしょうか?
B: いいアイデアですね。それでは,偶数の出目が5回のうち4回以上出現した場合,現在の得点に10点を追加するのはどうでしょう?
A: 最後に大逆転が起きる可能性が出てきますね。
B: そうすると,プログラムを少し改変する必要がありますね。
A: まず(02)行目に偶数の出目が出た回数をカウントするための変数 gusu を設定します。初期値には0を設定し,(09)行目には偶数の出現回数をカウントするプログラムを追加したのが,偶数の出現回数を追加したプログラム(図3)です。
(図3)
(01) score = 0
(02) gusu = 0
(03) i を 1 から 5 まで 1 ずつ増やしながら繰り返す:
(04) dice = キ
(05) もし ク ならば:
(06) score = ケ + 2
(07) そうでなければ:
(08) score = ケ - 3
(09) gusu = コ
(10) 表示する(”偶数回数:”, gusu)
(11) 表示する(”最終スコア:”, score)
B: さらに,ボーナスポイントを加算する条件を設定する必要がありますね。
【追加条件】
もし サ ならば:
score = ケ + 10
(図4 追加条件のプログラム)
A: 追加条件のプログラム(図4)は偶数の出現回数を追加したプログラム(図3)の シ 行目の下に入れると完成ですね。
生徒(A)と生徒(B)は最後にプログラムを実行したところ,正しく得点が計算されていることを確認できた。
A: プログラムを作るのは大変だけど,一度作ると繰り返し行う計算を自動化することで時間を短縮することができますね。
B: さらにルールを途中で変更できる場合,プログラムを少し改変するだけで何度も繰り返し使えると再利用性や拡張性も高いですね。情報の授業でプログラミングを学習してよかったですね。
【コ】の解答群
⓪ gusu ① gusu + 1 ② gusu + score ③ gusu + dice
【サ】の解答群
⓪ gusu > 4 ① gusu < 4 ② gusu >= 4 ③ gusu <= 4
【シ】の解答群
⓪ 3 ① 5 ② 8 ③ 9
この動画を見る
第3問 次の問い(問1~3)に答えよ。
問1
次の生徒(A)と生徒(B)の会話文を読み,空欄 ア・ウ に当てはまる数字を答えよ。また,空欄 イ・エ に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
A:昨日の放課後,友人Cとサイコロを使ったゲームで盛り上がったのですが,今から一緒にそのサイコロゲームをしませんか?
B:いいですね。どんなゲームなのかルールを教えてください。
A:参加プレイヤーは1つのサイコロを5回振ります。サイコロを振った際の出目(出目)が奇数(1,3,5)であれば2ポイントが得点に加算されます。サイコロの出目が偶数(2,4,6)であれば3ポイントが得点から減算されます。この作業を5回繰り返したときの最終的な得点が最も高い人の勝ちというシンプルなゲームです。
B:なるほど,シンプルなルールですね。
A:例えば,サイコロを2回振った際の出目が3,4の順である場合の得点は,奇数が1回,偶数が1回出ているので,得点は-1点となり,残り3回サイコロを振った出目が1,5,4の順に出た場合の最終的な得点は[ア]点となります。
B:得点の計算方法も理解できたので,2人で今から対決してみませんか?
A:いいですね。でも,サイコロを持っていないので,情報の授業で学習したプログラミングを使って,このゲームをパソコン上で動くようにしてみましょう。
B:そうですね。せっかく授業で学んだプログラミングの知識をここで発揮しましょう。まずは何から考えていけばよいと思いますか?
A:今回使用するサイコロの目を出力する必要があるため,関数のプログラムを作って,サイコロを再現する方法を考えましょう。以下は,乱数を使う場合の関数の説明です。
【関数の説明と例】
乱数(値)・・・0から引数として与えられた値までの範囲内で,ランダムな数値が生成され,その値が戻り値となる。
例:引数が3なら戻り値は0から3までの整数となる。
A:例えば,乱数(2)という関数を実行すると,[イ]が戻り値の候補となります。サイコロの出目は1から6なので,関数にも少し工夫が必要です。
B:サイコロの出目を再現できるようになったら,次はサイコロの出目が奇数か偶数かを判定するプログラムが必要ですね。
A:偶数か奇数かを判定する方法は,判定したい値を[ウ]で割った余りを調べるとよいですね。奇数の場合は[ウ]で割った余りが1,偶数の場合は[ウ]で割った余りが0になります。例えば,3は奇数であり,4は偶数であることが判定できます。
B:この判定を行うとると,プログラムの中で余りを計算する必要がありますが,どうしたらいいですか?
A:プログラムには色々な演算子(表1)があります。これらの演算子を利用して余りを求めることができますね。
表1 演算子の種類と使用例
| 種類 | 演算子 | 計算例 | 答え |
| 加算 | + | 1+2 | 3 |
| 減算 | - | 5-3 | 2 |
| 乗算 | × | 3×2 | 6 |
| 除算 | / | 8/2 | 4 |
| 余り | % | 7%2 | 1 |
B:例えば,2つの値を足す場合は+の演算子を使い,割り算を行う場合は[エ]の演算子を使えばいいですね。
A:その通りです。演算子を使い分けることで,さまざまな計算を行うことができます。
[イ]の解答群
⓪ 0,2 ① 1,2 ② 0,1,2 ③ 1,2,3
[エ]の解答群
⓪ + ① - ② × ③ / ④ %
問2 次の文章の空欄 オ~ケ に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
B: うーん,もう少しプログラムを作るうえでヒントが欲しいですね。全体的な流れがわかるといいのですが。
A: それでは簡単なフローチャートを考えてみましょう(図1)。サイコロゲームの流れは,サイコロを振り,出目が偶数か奇数かを判定して,得点を計算する,といった行動を5回繰り返していますね。
(図1 サイコロゲームのフローチャート)
始め
score = 0
5回繰り返す
サイコロを振る
└─ NO → scoreから3減算
└─ YES → scoreに2加算
(分岐の菱形の中:オ)
得点表示
終わり
B: フローチャートは処理の流れが可視化されて,わかりやすいですね。分岐には オ を入れればいいですね。
AさんとBさんは,これまでのヒントからプログラムを考えてみた(図2)。変数scoreには得点を求めるため初期値として0を,変数diceにはサイコロの目を求める関数を設定している。
(図2 サイコロゲームの得点を計算するプログラム)
(01) score = 0
(02) i を 1 から カ ながら繰り返す:
(03) dice = キ
(04) もし ク ならば:
(05) score = ケ + 2
(06) そうでなければ:
(07) score = ケ - 3
(08) 表示する(”得点:”, score)
オ の解答群
⓪ 出目が偶数 ① 出目が奇数 ② score が 0 ③ score が 1
カ の解答群
⓪ 5まで1ずつ増やし ① 6まで1ずつ増やし ② 5まで1ずつ減らし ③ 6まで1ずつ減らし
キ の解答群
⓪ 乱数(5) ① 乱数(6) ② 乱数(5) + 1 ③ 乱数(6) + 1
ク の解答群
⓪ dice % 2 == 0 ① dice % 2 == 1 ② score % 2 == 0 ③ score % 2 == 1
ケ の解答群
⓪ score ① dice ② i ③ i + 1
問3 次の文章を参考に,図3のプログラムの空欄【コ—シ】に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
A: プログラム(図2)が完成しました。これでサイコロゲームがコンピュータでも実行できるようになりました。
B: プログラムを動かしてみましょう。【2人でプログラムを実行してみた】
【実行結果】
Aさんの表示 得点:0
Bさんの表示 得点:5
A: きちんと動きました。Bさんの勝ちですね。もう少し白熱するようにゲームの要素を追加しませんか? 最後に特定の条件を満たした場合にボーナスポイントを与えるのはどうでしょうか?
B: いいアイデアですね。それでは,偶数の出目が5回のうち4回以上出現した場合,現在の得点に10点を追加するのはどうでしょう?
A: 最後に大逆転が起きる可能性が出てきますね。
B: そうすると,プログラムを少し改変する必要がありますね。
A: まず(02)行目に偶数の出目が出た回数をカウントするための変数 gusu を設定します。初期値には0を設定し,(09)行目には偶数の出現回数をカウントするプログラムを追加したのが,偶数の出現回数を追加したプログラム(図3)です。
(図3)
(01) score = 0
(02) gusu = 0
(03) i を 1 から 5 まで 1 ずつ増やしながら繰り返す:
(04) dice = キ
(05) もし ク ならば:
(06) score = ケ + 2
(07) そうでなければ:
(08) score = ケ - 3
(09) gusu = コ
(10) 表示する(”偶数回数:”, gusu)
(11) 表示する(”最終スコア:”, score)
B: さらに,ボーナスポイントを加算する条件を設定する必要がありますね。
【追加条件】
もし サ ならば:
score = ケ + 10
(図4 追加条件のプログラム)
A: 追加条件のプログラム(図4)は偶数の出現回数を追加したプログラム(図3)の シ 行目の下に入れると完成ですね。
生徒(A)と生徒(B)は最後にプログラムを実行したところ,正しく得点が計算されていることを確認できた。
A: プログラムを作るのは大変だけど,一度作ると繰り返し行う計算を自動化することで時間を短縮することができますね。
B: さらにルールを途中で変更できる場合,プログラムを少し改変するだけで何度も繰り返し使えると再利用性や拡張性も高いですね。情報の授業でプログラミングを学習してよかったですね。
【コ】の解答群
⓪ gusu ① gusu + 1 ② gusu + score ③ gusu + dice
【サ】の解答群
⓪ gusu > 4 ① gusu < 4 ② gusu >= 4 ③ gusu <= 4
【シ】の解答群
⓪ 3 ① 5 ② 8 ③ 9
【情報Ⅰ】最小硬貨枚数を計算するプログラムを解説

単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の生徒(S)と先生(T)の会話文を読み、空欄〔ア〕に当てはまる数字をマークせよ。
また、空欄〔イ〕〜〔エ〕に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。ただし、空欄〔ウ〕・〔エ〕は解答の順序は問わない
S:この前、お客さんが460円の商品を買うのに、510円を払って、釣り銭を50円受け取っていたのを見て、授業で勉強したプログラミングで、そんな「上手な払い方」を計算するプログラムを作ってみたいなと思いました。
T:いいですね。「上手な払い方」とは何を考える必要がありますね。
S:普通は手持ちの硬貨の枚数を少なくするような払い方でしょうか。
T:そうですね。ただ、ここでは、客が支払う枚数と釣り銭を受け取る枚数の合計を最小にする払い方を考えてみませんか?客も店も十分な枚数の効果を持っていると仮定しましょう。計算を簡単にするために、100円以下の買い物とし、使う硬貨は1円玉、5円玉、10円玉、50円玉、100円玉のみで500円玉は使わない場合を考えてみましょう。
例えば、46円をちょうど支払う場合、支払い枚数はどうなりますか?
S:46円を支払うには、10円玉4枚、5円玉1枚、1円玉1枚という6枚で払い方が最小の枚数になります。
T:そうですね。一方、同じ46円を支払うのに、51円を支払って釣り銭5円受け取る払い方では、支払いに2枚、釣り銭に1枚で、合計3枚の硬貨のやりとりになります。こうすると交換する硬貨の枚数の合計が最小になりますね。
S:これが上手な払い方ですね。
T:そうです。このように、客と店員が交換する硬貨の合計が最小となる枚数、すなわち「最小交換硬貨枚数」の計算を考えましょう。
S:どうやって考えればいいかなぁ。
T:ここでは、次の関数のプログラムを作り、それを使う方法を考えてみましょう。目標の金額を釣り銭無くちょうど支払うために必要な最小の硬貨枚数を求める関数です。
【関数の説明と例】
枚数(金額)…引数として「金額」が与えられ、ちょうどその金額となる硬貨の組合せの中で、枚数が最小となる硬貨枚数が戻り値となる関数。
例:8円は「5円玉が1枚と1円玉が3枚」の組合せで最小の硬貨枚数になるので、枚数(8)の値は4となる。
これは、例えば、枚数(46)=〔ア〕 と計算してくれるような関数です。これを使って最小交換硬貨枚数の計算を考えてみましょう。例えば、46円を支払うのに、51円払って5円の釣り銭を受け取る払い方をした場合、客と店員の間で交換される硬貨枚数の合計は、この関数を使うと、どのように計算できますか?
S:〔イ〕で求められますね。
T:一般に、商品の価格x円に対して釣り銭y円を0,1,2,・・・と変化させて、それぞれの場合に必要な硬貨の枚数の合計を
枚数(〔ウ〕)+枚数(〔エ〕)と計算し、一番小さな値を最小交換硬貨枚数とすればよいのです。
S:なるほど。それで、釣り銭yはいくらまで調べればよいでしょうか?
T:面白い数字パズルですね。まあ、詳しくは今度考えるとして、今回は100円以下の商品なのでyは99まで調べれば十分でしょう。
【イの解答群】
⓪ 枚数(51)+枚数(5)
① 枚数(46)+枚数(5)
② 枚数(51)−枚数(5)
③ 枚数(46)−枚数(5)
【ウ・エの解答群】
⓪ x
① y
② x+y
③ x−y
問2
次の文章の空欄〔オ〕〜〔コ〕に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
S:まずは、関数「枚数(金額)」のプログラムを作るために、与えられた金額ちょうどになる最小の硬貨枚数を計算するプログラムを考えてみます。もう少しヒントが欲しいなぁ。
T:金額に対して、高額の硬貨から使うように考えて枚数と残金を計算していくとよいでしょう。また、金額に対して、ある額の硬貨が何枚まで使えて、残金がいくらになるかを計算するには、整数値の商を求める演算「÷」とその余りを求める演算「%」が使えるでしょう。例えば、46円に対して10円玉が何枚まで使えるかは〔オ〕で、その際にいくら残るかは〔カ〕で求めることができますね。
S:なるほど!あとは自分でできそうです。
Sさんは、先生(T)との会話からヒントを得て、変数 kingaku に与えられた目標の金額(100円以下)に対し、その金額ちょうどになる最小の硬貨枚数を計算するプログラムを考えてみた(図1)。ここでは例として目標の金額を46円としている。
配列 kouka に硬貨の単位を小さい順に設定している。なお、配列の添え字は0から始まるものとする。最低額の硬貨が1円玉なのでkouka[0]の値は1となる。
先生(T)のヒントに従い、高額の硬貨から何枚まで使えるかを計算する方針で、(4)〜(6)行目のような繰り返し文にした。この繰り返しで、変数 maisu に支払う硬貨の枚数の合計が計算され、変数 nokori に残りいくら支払えればよいか、という残金が計算される。
実行してみると〔ア〕が表示されたので、正しく計算できていることが分かる。いろいろな例で試してみたが、すべて正しく計算できていることを確認できた。
(図1)目標の金額ちょうどになる最小の硬貨枚数を計算するプログラム
(1) kouka = [1,5,10,50,100]
(2) kingaku = 46
(3) maisu = 0, nokori = kingaku
(4) 〔i〕を 〔キ〕 ながら繰り返す:
(5) maisu = 〔ク〕 + 〔ケ〕
(6) nokori = 〔コ〕
(7) 表示する(maisu)
【オ・カの解答群】
⓪ 46 ÷ 10 + 1
① 46 % 10 − 1
② 46 ÷ 10
③ 46 % 10
【キの解答群】
⓪ 5から1まで1ずつ減らし
① 4から0まで1ずつ減らし
② 0から4まで1ずつ増やし
③ 1から5まで1ずつ増やし
【クの解答群】
⓪ 1
① maisu
② i
③ nokori
【ケ・コの解答群】
⓪ nokori ÷ Kouka[i]
① nokori % Kouka[i]
② maisu ÷ Kouka[i]
③ maisu % Kouka[i]
問3
次の文章を参考に、図2のプログラムの空欄〔サ〕〜〔タ〕に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。ただし、空欄〔ス〕・〔セ〕は解答の順序は問わない。
T:プログラム(図1)ができたようですね。それを使えば、関数「枚数(金額)」のプログラムができます。関数の引数として与えられる金額の値をプログラム(図1)の変数 kingaku に設定し、(7)行目の代わりに変数 maisu の値を関数の戻り値とすれば、関数「枚数(金額)」のプログラムとなります。では、その関数を使って最小交換硬貨枚数を計算するプログラムを作ってみましょう。ここでも、100円以下の買い物として考えてみます。
【関数の説明(再掲)】
枚数(金額)…引数として「金額」が与えられ、ちょうどその金額となる硬貨の組合せの中で、枚数が最小となる硬貨枚数が戻り値となる関数。
Sさんは、図2のようなプログラムを作成した。変数 kakaku に与えられる商品の価格に対して、釣り銭を変数 tsuri を用意し、妥当な tsuri のすべての値に対して交換する硬貨の枚数を調べ、その最小値を求めるプログラムである。なお、ここでは例として商品の価格を46円としている。
このプログラムでは、先生(T)のアドバイスに従い、釣り銭無しの場合も含め、99円までのすべての釣り銭に対し、その釣り銭になるように支払う場合に交換される硬貨の枚数を求め、その最小値を最小交換硬貨枚数として計算している。
最小値の計算では、これまでの払い方での最小枚数を変数 min_maisu に記憶しておき、それより少ない枚数の払い方が出るたびに更新している。min_maisuの初期値には、十分大きな値として100を用いている。100円以下の買い物では、使う硬貨の枚数は100枚を超えないからである。
(図2)最小交換硬貨枚数を求めるプログラム
(1) kakaku = 46
(2) min_maisu = 100
(3) 〔サ〕を 〔ジ〕 から 99 まで1ずつ増やしながら繰り返す:
(4) shiharai = kakaku + tsuri
(5) maisu = 〔ス〕 + 〔セ〕
(6) もし 〔ソ〕 < min_maisu ならば:
(7) 〔タ〕 = 〔ソ〕
(8) 表示する(min_maisu)
このプログラムを実行してみたところ3が表示された。46円を支払うときの最小交換硬貨枚数は、支払いで50円玉が1枚、1円玉が1枚、釣り銭で5円玉が1枚の計3枚なので、正しく計算できていることが分かる。同様に、kakaku の値をいろいろと変えて実行してみたところ、すべて正しく計算できていることを確認できた。
【サ・ソ・タの解答群】
⓪ maisu
① min_maisu
② shiharai
③ tsuri
【シの解答群】
⓪ 0
① 1
② 99
③ 100
【ス・セの解答群】
⓪ 枚数(shiharai)
① 枚数(kakaku)
② 枚数(tsuri)
③ shiharai
④ kakaku
⑤ tsuri
この動画を見る
次の生徒(S)と先生(T)の会話文を読み、空欄〔ア〕に当てはまる数字をマークせよ。
また、空欄〔イ〕〜〔エ〕に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。ただし、空欄〔ウ〕・〔エ〕は解答の順序は問わない
S:この前、お客さんが460円の商品を買うのに、510円を払って、釣り銭を50円受け取っていたのを見て、授業で勉強したプログラミングで、そんな「上手な払い方」を計算するプログラムを作ってみたいなと思いました。
T:いいですね。「上手な払い方」とは何を考える必要がありますね。
S:普通は手持ちの硬貨の枚数を少なくするような払い方でしょうか。
T:そうですね。ただ、ここでは、客が支払う枚数と釣り銭を受け取る枚数の合計を最小にする払い方を考えてみませんか?客も店も十分な枚数の効果を持っていると仮定しましょう。計算を簡単にするために、100円以下の買い物とし、使う硬貨は1円玉、5円玉、10円玉、50円玉、100円玉のみで500円玉は使わない場合を考えてみましょう。
例えば、46円をちょうど支払う場合、支払い枚数はどうなりますか?
S:46円を支払うには、10円玉4枚、5円玉1枚、1円玉1枚という6枚で払い方が最小の枚数になります。
T:そうですね。一方、同じ46円を支払うのに、51円を支払って釣り銭5円受け取る払い方では、支払いに2枚、釣り銭に1枚で、合計3枚の硬貨のやりとりになります。こうすると交換する硬貨の枚数の合計が最小になりますね。
S:これが上手な払い方ですね。
T:そうです。このように、客と店員が交換する硬貨の合計が最小となる枚数、すなわち「最小交換硬貨枚数」の計算を考えましょう。
S:どうやって考えればいいかなぁ。
T:ここでは、次の関数のプログラムを作り、それを使う方法を考えてみましょう。目標の金額を釣り銭無くちょうど支払うために必要な最小の硬貨枚数を求める関数です。
【関数の説明と例】
枚数(金額)…引数として「金額」が与えられ、ちょうどその金額となる硬貨の組合せの中で、枚数が最小となる硬貨枚数が戻り値となる関数。
例:8円は「5円玉が1枚と1円玉が3枚」の組合せで最小の硬貨枚数になるので、枚数(8)の値は4となる。
これは、例えば、枚数(46)=〔ア〕 と計算してくれるような関数です。これを使って最小交換硬貨枚数の計算を考えてみましょう。例えば、46円を支払うのに、51円払って5円の釣り銭を受け取る払い方をした場合、客と店員の間で交換される硬貨枚数の合計は、この関数を使うと、どのように計算できますか?
S:〔イ〕で求められますね。
T:一般に、商品の価格x円に対して釣り銭y円を0,1,2,・・・と変化させて、それぞれの場合に必要な硬貨の枚数の合計を
枚数(〔ウ〕)+枚数(〔エ〕)と計算し、一番小さな値を最小交換硬貨枚数とすればよいのです。
S:なるほど。それで、釣り銭yはいくらまで調べればよいでしょうか?
T:面白い数字パズルですね。まあ、詳しくは今度考えるとして、今回は100円以下の商品なのでyは99まで調べれば十分でしょう。
【イの解答群】
⓪ 枚数(51)+枚数(5)
① 枚数(46)+枚数(5)
② 枚数(51)−枚数(5)
③ 枚数(46)−枚数(5)
【ウ・エの解答群】
⓪ x
① y
② x+y
③ x−y
問2
次の文章の空欄〔オ〕〜〔コ〕に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
S:まずは、関数「枚数(金額)」のプログラムを作るために、与えられた金額ちょうどになる最小の硬貨枚数を計算するプログラムを考えてみます。もう少しヒントが欲しいなぁ。
T:金額に対して、高額の硬貨から使うように考えて枚数と残金を計算していくとよいでしょう。また、金額に対して、ある額の硬貨が何枚まで使えて、残金がいくらになるかを計算するには、整数値の商を求める演算「÷」とその余りを求める演算「%」が使えるでしょう。例えば、46円に対して10円玉が何枚まで使えるかは〔オ〕で、その際にいくら残るかは〔カ〕で求めることができますね。
S:なるほど!あとは自分でできそうです。
Sさんは、先生(T)との会話からヒントを得て、変数 kingaku に与えられた目標の金額(100円以下)に対し、その金額ちょうどになる最小の硬貨枚数を計算するプログラムを考えてみた(図1)。ここでは例として目標の金額を46円としている。
配列 kouka に硬貨の単位を小さい順に設定している。なお、配列の添え字は0から始まるものとする。最低額の硬貨が1円玉なのでkouka[0]の値は1となる。
先生(T)のヒントに従い、高額の硬貨から何枚まで使えるかを計算する方針で、(4)〜(6)行目のような繰り返し文にした。この繰り返しで、変数 maisu に支払う硬貨の枚数の合計が計算され、変数 nokori に残りいくら支払えればよいか、という残金が計算される。
実行してみると〔ア〕が表示されたので、正しく計算できていることが分かる。いろいろな例で試してみたが、すべて正しく計算できていることを確認できた。
(図1)目標の金額ちょうどになる最小の硬貨枚数を計算するプログラム
(1) kouka = [1,5,10,50,100]
(2) kingaku = 46
(3) maisu = 0, nokori = kingaku
(4) 〔i〕を 〔キ〕 ながら繰り返す:
(5) maisu = 〔ク〕 + 〔ケ〕
(6) nokori = 〔コ〕
(7) 表示する(maisu)
【オ・カの解答群】
⓪ 46 ÷ 10 + 1
① 46 % 10 − 1
② 46 ÷ 10
③ 46 % 10
【キの解答群】
⓪ 5から1まで1ずつ減らし
① 4から0まで1ずつ減らし
② 0から4まで1ずつ増やし
③ 1から5まで1ずつ増やし
【クの解答群】
⓪ 1
① maisu
② i
③ nokori
【ケ・コの解答群】
⓪ nokori ÷ Kouka[i]
① nokori % Kouka[i]
② maisu ÷ Kouka[i]
③ maisu % Kouka[i]
問3
次の文章を参考に、図2のプログラムの空欄〔サ〕〜〔タ〕に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。ただし、空欄〔ス〕・〔セ〕は解答の順序は問わない。
T:プログラム(図1)ができたようですね。それを使えば、関数「枚数(金額)」のプログラムができます。関数の引数として与えられる金額の値をプログラム(図1)の変数 kingaku に設定し、(7)行目の代わりに変数 maisu の値を関数の戻り値とすれば、関数「枚数(金額)」のプログラムとなります。では、その関数を使って最小交換硬貨枚数を計算するプログラムを作ってみましょう。ここでも、100円以下の買い物として考えてみます。
【関数の説明(再掲)】
枚数(金額)…引数として「金額」が与えられ、ちょうどその金額となる硬貨の組合せの中で、枚数が最小となる硬貨枚数が戻り値となる関数。
Sさんは、図2のようなプログラムを作成した。変数 kakaku に与えられる商品の価格に対して、釣り銭を変数 tsuri を用意し、妥当な tsuri のすべての値に対して交換する硬貨の枚数を調べ、その最小値を求めるプログラムである。なお、ここでは例として商品の価格を46円としている。
このプログラムでは、先生(T)のアドバイスに従い、釣り銭無しの場合も含め、99円までのすべての釣り銭に対し、その釣り銭になるように支払う場合に交換される硬貨の枚数を求め、その最小値を最小交換硬貨枚数として計算している。
最小値の計算では、これまでの払い方での最小枚数を変数 min_maisu に記憶しておき、それより少ない枚数の払い方が出るたびに更新している。min_maisuの初期値には、十分大きな値として100を用いている。100円以下の買い物では、使う硬貨の枚数は100枚を超えないからである。
(図2)最小交換硬貨枚数を求めるプログラム
(1) kakaku = 46
(2) min_maisu = 100
(3) 〔サ〕を 〔ジ〕 から 99 まで1ずつ増やしながら繰り返す:
(4) shiharai = kakaku + tsuri
(5) maisu = 〔ス〕 + 〔セ〕
(6) もし 〔ソ〕 < min_maisu ならば:
(7) 〔タ〕 = 〔ソ〕
(8) 表示する(min_maisu)
このプログラムを実行してみたところ3が表示された。46円を支払うときの最小交換硬貨枚数は、支払いで50円玉が1枚、1円玉が1枚、釣り銭で5円玉が1枚の計3枚なので、正しく計算できていることが分かる。同様に、kakaku の値をいろいろと変えて実行してみたところ、すべて正しく計算できていることを確認できた。
【サ・ソ・タの解答群】
⓪ maisu
① min_maisu
② shiharai
③ tsuri
【シの解答群】
⓪ 0
① 1
② 99
③ 100
【ス・セの解答群】
⓪ 枚数(shiharai)
① 枚数(kakaku)
② 枚数(tsuri)
③ shiharai
④ kakaku
⑤ tsuri
【情報Ⅰ】大学入学共通テスト対応プログラム表記で学ぶ!条件分岐の基礎からくじ引きプログラムまで解説

単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計
指導講師:
理数個別チャンネル
問題文全文(内容文):
問1 次の文章を読み、空欄ア〜キに入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
生徒:今度の文化祭でくじ引き大会をすることになりました。せっかくなので、くじ引きプログラミングを作りたいのですが、何から始めたらいいんですか。
先生:それはいいですね! まずは、大学入学共通テスト用のプログラム表記を使って条件分岐から学んでいきましょう。
例えば、正六面体のサイコロを振って3が出たら「当たり!」と表示し、それ以外なら「はずれ」と表示されるプログラムは次のようになります。
(01) saikoro = 3 # サイコロの出目
(02) もし ア ならば:
(03) 表示する(“当たり!”)
(04) そうでなければ:
(05) 表示する(“はずれ”)
生徒:なるほど! サイコロの出目が1なら「1等」、2〜3なら「2等」、それ以外なら「はずれ」と表示するのは、次のようになりますね。
(01) saikoro = 3 # サイコロの出目
(02) もし イ ならば:
(03) 表示する(“1等”)
(04) そうでなくもし ウ ならば:
(05) 表示する(“2等”)
(06) そうでなければ:
(07) 表示する(“はずれ”)
ア・イ・ウの解答群
| 0 saikoro == 0 | 1 saikoro == 1 | 2 saikoro == 2 |
| 3 saikoro == 3 | 4 saikoro <= 3 | 5 saikoro <= 3 |
| 6 saikoro > 3 | 7 saikoro < 3 |
先生:その通り。このままだと1行目の変数saikoroの値を手入力する必要があるので、乱数を使うといいですね。次の乱数関数を使っていきましょう。
f 乱数の説明
乱数(n)…0から引数として与えられた整数の中からランダムに1つ返却する。
生徒:ということは,1行目を以下のように変更すればよいですね。
(01) saikoro = エ
エ の解答群
| 0 乱数(6) | 1 乱数(5) | 2 乱数(6)+1 | 3 乱数(5)+1 |
先生:その通り。では今度は配列を使って景品を表示するプログラムを作成していきましょう。サイコロの目の数に対応するように配列Keihinを作成します。はずれの場合も,アメを渡すとしましょう。
配列名:Keihin プラモ ポテチ チョコ アメ アメ アメ
このとき添字が0から始まるとした場合,先頭から数えて3番目のチョコの要素を取り出したい場合は以下のように記述すればいいですね。
item = オ
オ の解答群
| 0 Keihin+3 | 1 Keihin[3] | 2 Keihin[2] | 3 Keihin[0] |
先生:実際はサイコロの目と対応しているので,景品を表示する場合は9行目のように記述します。
(01) Keihin = ["プラモ","ポテチ","チョコ","アメ","アメ","アメ"]
(02) saikoro = エ # サイコロの出目
(03) もし イ ならば:
(04) 表示する(“1等”)
(05) そうでなくもし ウ ならば:
(06) 表示する(“2等”)
(07) そうでなければ:
(08) 表示する(“はずれ”)
(09) 表示する(“景品:”, カ)
カ の解答群
| 0 Keihin[saikoro] | 1 Keihin[saikoro-1] | 2 Keihin[1] | 3 Keihin[saikoro+1] |
生徒:完成しましたね! ただ、一人3回くじを引かせたいです。
先生:それなら、処理全体を繰り返し文で囲むといいですね。3行目の処理で、何回目のくじ引きかも表示するようにしましょう。
(01) Keihin = ["プラモ","ポテチ","チョコ","アメ","アメ","アメ"]
(02) i を キ
(03) 表示する(i+1,"回目")
(04) saikoro = エ # サイコロの出目
(05) もし イ ならば:
(06) 表示する(“1等”)
(07) そうでなくもし ウ ならば:
(08) 表示する(“2等”)
(09) そうでなければ:
(10) 表示する(“はずれ”)
(11) 表示する(“景品:”, カ)
キ の解答群
| 0 0から2まで1ずつ増やしながら繰り返す |
| 1 0から3まで1ずつ増やしながら繰り返す |
| 2 2から6まで1ずつ減らしながら繰り返す |
| 3 1から3まで1ずつ増やしながら繰り返す |
生徒:ループの中に条件分岐があると難しく感じますが、1つ1つを順番に作っていったので理解できました!
先生:大学入学共通テストの「情報Ⅰ」でも、このように入れ子構造で出題される可能性があります。いきなり全体を見ると難しく感じますが、処理の内容を1つ1つ押さえて、この構造に慣れていきましょう。
この動画を見る
問1 次の文章を読み、空欄ア〜キに入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
生徒:今度の文化祭でくじ引き大会をすることになりました。せっかくなので、くじ引きプログラミングを作りたいのですが、何から始めたらいいんですか。
先生:それはいいですね! まずは、大学入学共通テスト用のプログラム表記を使って条件分岐から学んでいきましょう。
例えば、正六面体のサイコロを振って3が出たら「当たり!」と表示し、それ以外なら「はずれ」と表示されるプログラムは次のようになります。
(01) saikoro = 3 # サイコロの出目
(02) もし ア ならば:
(03) 表示する(“当たり!”)
(04) そうでなければ:
(05) 表示する(“はずれ”)
生徒:なるほど! サイコロの出目が1なら「1等」、2〜3なら「2等」、それ以外なら「はずれ」と表示するのは、次のようになりますね。
(01) saikoro = 3 # サイコロの出目
(02) もし イ ならば:
(03) 表示する(“1等”)
(04) そうでなくもし ウ ならば:
(05) 表示する(“2等”)
(06) そうでなければ:
(07) 表示する(“はずれ”)
ア・イ・ウの解答群
| 0 saikoro == 0 | 1 saikoro == 1 | 2 saikoro == 2 |
| 3 saikoro == 3 | 4 saikoro <= 3 | 5 saikoro <= 3 |
| 6 saikoro > 3 | 7 saikoro < 3 |
先生:その通り。このままだと1行目の変数saikoroの値を手入力する必要があるので、乱数を使うといいですね。次の乱数関数を使っていきましょう。
f 乱数の説明
乱数(n)…0から引数として与えられた整数の中からランダムに1つ返却する。
生徒:ということは,1行目を以下のように変更すればよいですね。
(01) saikoro = エ
エ の解答群
| 0 乱数(6) | 1 乱数(5) | 2 乱数(6)+1 | 3 乱数(5)+1 |
先生:その通り。では今度は配列を使って景品を表示するプログラムを作成していきましょう。サイコロの目の数に対応するように配列Keihinを作成します。はずれの場合も,アメを渡すとしましょう。
配列名:Keihin プラモ ポテチ チョコ アメ アメ アメ
このとき添字が0から始まるとした場合,先頭から数えて3番目のチョコの要素を取り出したい場合は以下のように記述すればいいですね。
item = オ
オ の解答群
| 0 Keihin+3 | 1 Keihin[3] | 2 Keihin[2] | 3 Keihin[0] |
先生:実際はサイコロの目と対応しているので,景品を表示する場合は9行目のように記述します。
(01) Keihin = ["プラモ","ポテチ","チョコ","アメ","アメ","アメ"]
(02) saikoro = エ # サイコロの出目
(03) もし イ ならば:
(04) 表示する(“1等”)
(05) そうでなくもし ウ ならば:
(06) 表示する(“2等”)
(07) そうでなければ:
(08) 表示する(“はずれ”)
(09) 表示する(“景品:”, カ)
カ の解答群
| 0 Keihin[saikoro] | 1 Keihin[saikoro-1] | 2 Keihin[1] | 3 Keihin[saikoro+1] |
生徒:完成しましたね! ただ、一人3回くじを引かせたいです。
先生:それなら、処理全体を繰り返し文で囲むといいですね。3行目の処理で、何回目のくじ引きかも表示するようにしましょう。
(01) Keihin = ["プラモ","ポテチ","チョコ","アメ","アメ","アメ"]
(02) i を キ
(03) 表示する(i+1,"回目")
(04) saikoro = エ # サイコロの出目
(05) もし イ ならば:
(06) 表示する(“1等”)
(07) そうでなくもし ウ ならば:
(08) 表示する(“2等”)
(09) そうでなければ:
(10) 表示する(“はずれ”)
(11) 表示する(“景品:”, カ)
キ の解答群
| 0 0から2まで1ずつ増やしながら繰り返す |
| 1 0から3まで1ずつ増やしながら繰り返す |
| 2 2から6まで1ずつ減らしながら繰り返す |
| 3 1から3まで1ずつ増やしながら繰り返す |
生徒:ループの中に条件分岐があると難しく感じますが、1つ1つを順番に作っていったので理解できました!
先生:大学入学共通テストの「情報Ⅰ」でも、このように入れ子構造で出題される可能性があります。いきなり全体を見ると難しく感じますが、処理の内容を1つ1つ押さえて、この構造に慣れていきましょう。
2025年5月実施共通テスト模試「情報Ⅰ」大問3解説!

単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計#探索と整列のプログラム#プログラムによる動的シミュレーション
指導講師:
理数個別チャンネル
問題文全文(内容文):
2025年5月実施共通テスト模試「情報Ⅰ」大問3解説!
この動画を見る
2025年5月実施共通テスト模試「情報Ⅰ」大問3解説!
239 変数に文字列を代入する:文字列同士の足し算ってどういうこと!? #shorts
単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計#基本的なプログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
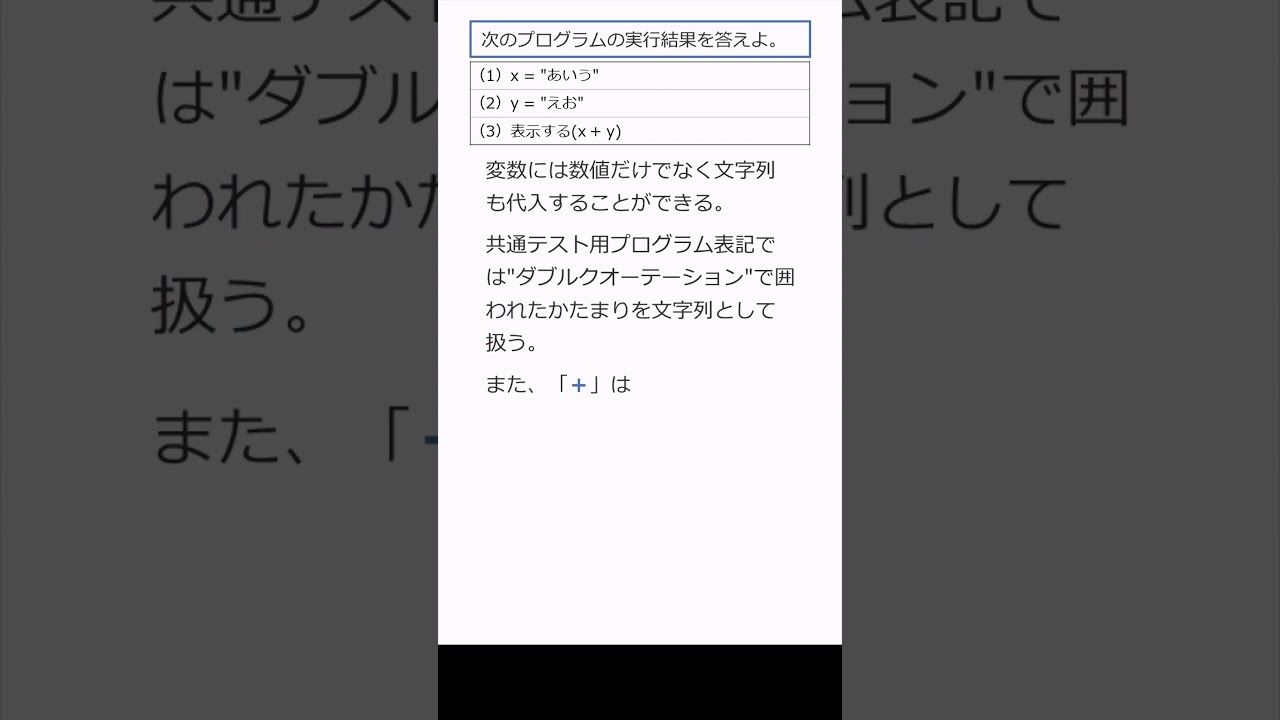
次のプログラムの実行結果を答えよ。
この動画を見る
次のプログラムの実行結果を答えよ。
237 x=x*xの実行結果とは:数学とプログラムの違いに注意しよう! #shorts
単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計#基本的なプログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
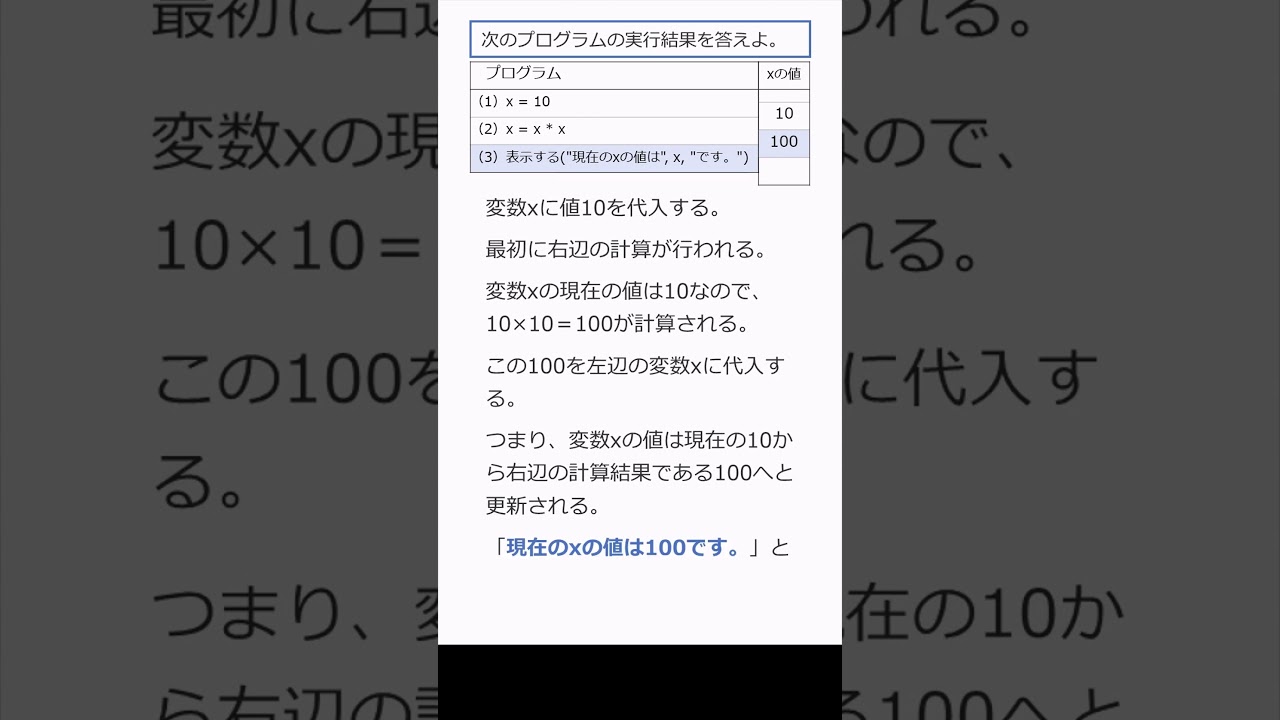
次のプログラムの実行結果を答えよ。
(1)x = 10
(2)x = x * x
(3)表示する("現在のxの値は", x, "です。")
この動画を見る
次のプログラムの実行結果を答えよ。
(1)x = 10
(2)x = x * x
(3)表示する("現在のxの値は", x, "です。")
236 x=x+1ってどういうこと!?:自身の値を更新するプログラム #shorts
単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計#基本的なプログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
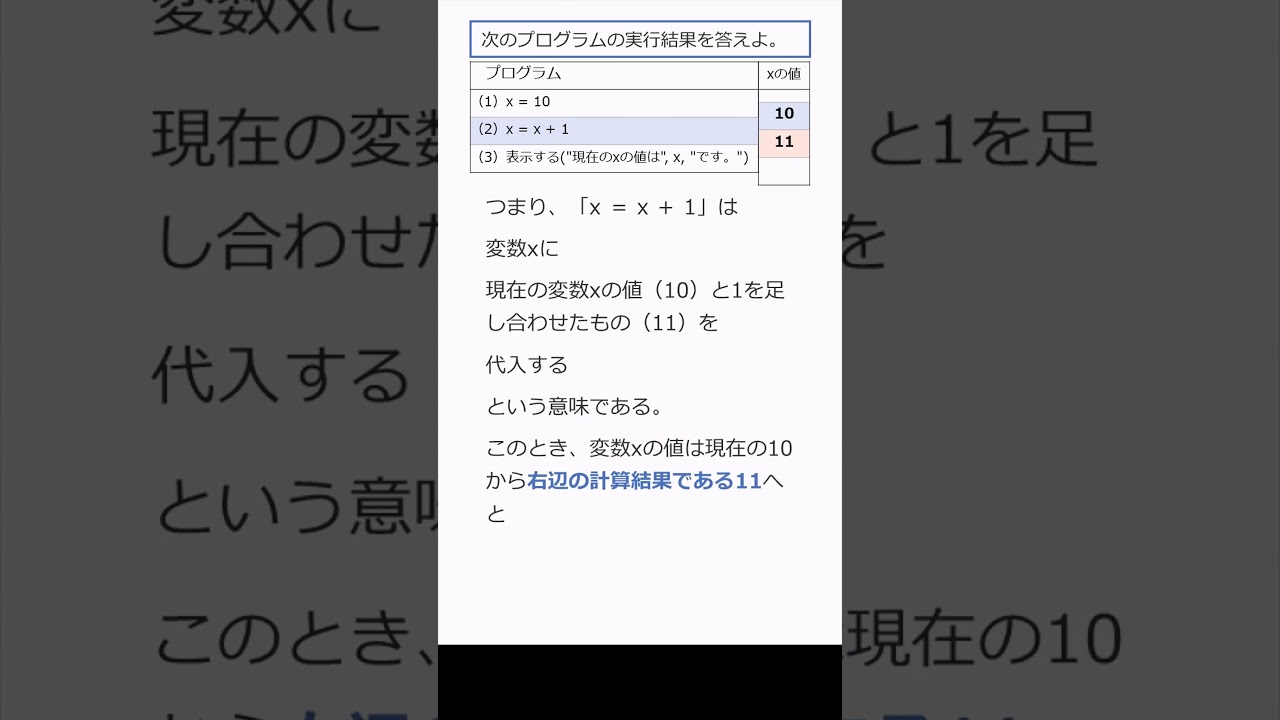
次のプログラムの実行結果を答えよ。
(1)x = 10
(2)x = x + 1
(3)表示する("現在のxの値は", x, "です。")
この動画を見る
次のプログラムの実行結果を答えよ。
(1)x = 10
(2)x = x + 1
(3)表示する("現在のxの値は", x, "です。")
235 変数の値の入れ替える基本技:一時待避用の変数tmpを使いこなそう! #shorts

単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計#基本的なプログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
次のプログラムの実行結果を答えよ。
(1)x = 1
(2)y = 2
(3)tmp = x
(4)x = y
(5)y = tmp
(6)表示する("現在のxの値は", x, "です。")
(7)表示する("現在のyの値は", y, "です。")
この動画を見る
次のプログラムの実行結果を答えよ。
(1)x = 1
(2)y = 2
(3)tmp = x
(4)x = y
(5)y = tmp
(6)表示する("現在のxの値は", x, "です。")
(7)表示する("現在のyの値は", y, "です。")
234 変数に別の変数の値を代入する:値の更新(上書き)をマスターしよう! #shorts

単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計#基本的なプログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
次のプログラムの実行結果を答えよ。
(1)x = 1
(2)y = 2
(3)x = y
(4)表示する("現在のxの値は", x, "です。")
(5)表示する("現在のyの値は", y, "です。")
この動画を見る
次のプログラムの実行結果を答えよ。
(1)x = 1
(2)y = 2
(3)x = y
(4)表示する("現在のxの値は", x, "です。")
(5)表示する("現在のyの値は", y, "です。")
233 値を代入した変数に別の値を代入する:上から下へと実行されていくプログラムの基本! #shorts
単元:
#情報Ⅰ(高校生)#デジタル#プログラミング#アルゴリズムの表し方とプログラムの設計#基本的なプログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
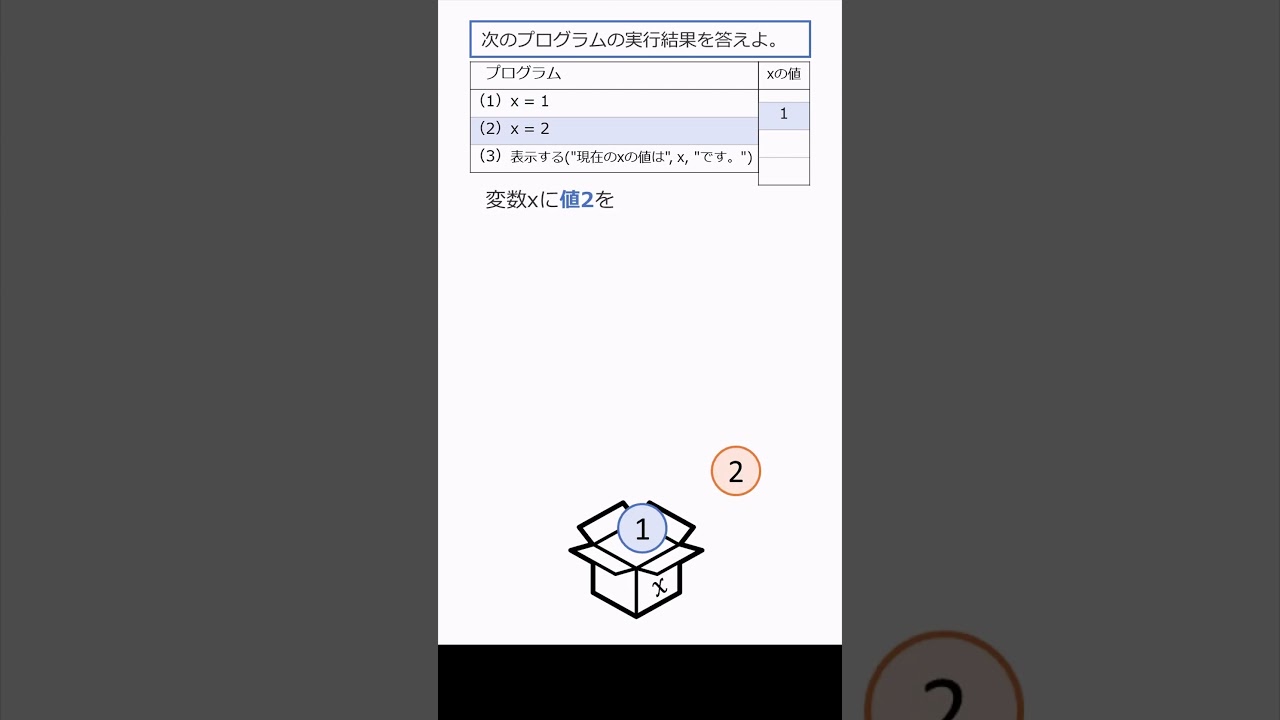
次のプログラムの実行結果を答えよ。
(1)x = 1
(2)x = 2
(3)表示する("現在のxの値は", x, "です。")
この動画を見る
次のプログラムの実行結果を答えよ。
(1)x = 1
(2)x = 2
(3)表示する("現在のxの値は", x, "です。")
232 プログラムでの計算順にご注意!:小さなミスでまったく違う結果になってしまうプログラムの繊細さ #shorts
単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計#基本的なプログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
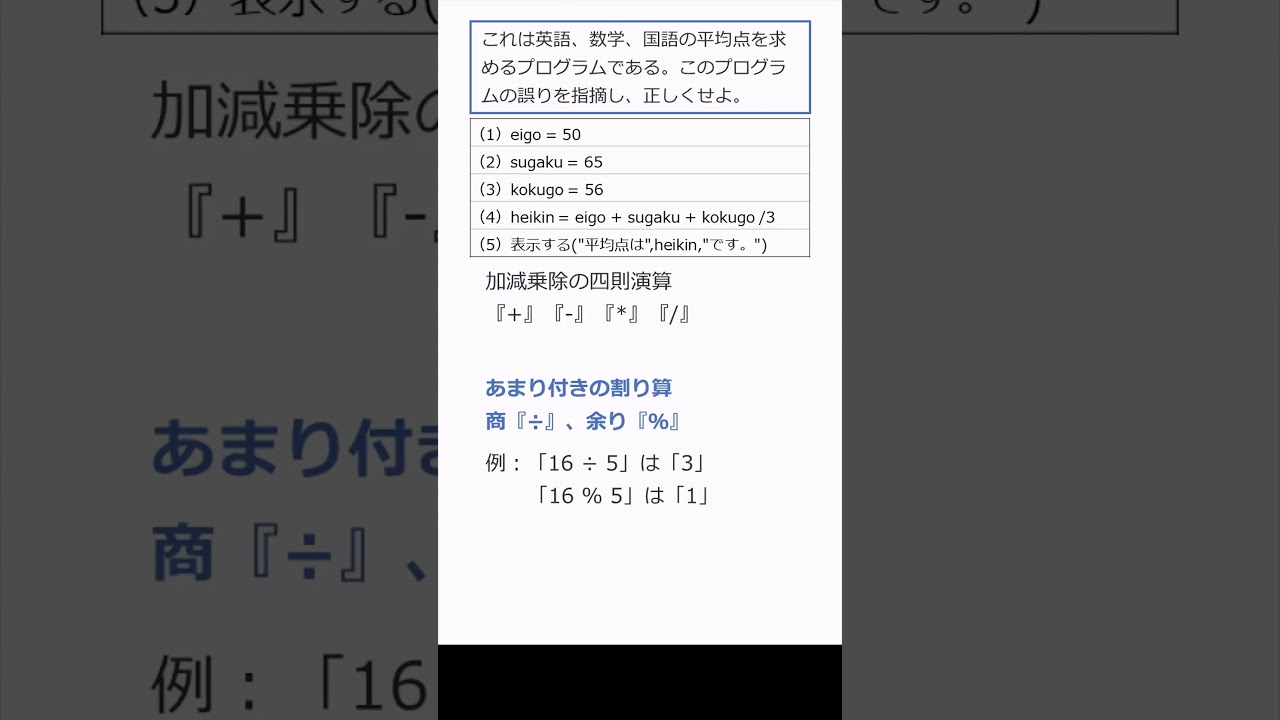
これは英語、数学、国語の平均点を求めるプログラムである。このプログラムの誤りを指摘し、正しくせよ。
(1)eigo = 50
(2)sugaku = 65
(3)kokugo = 56
(4)heikin = eigo + sugaku + kokugo /3
(5)表示する("平均点は",heikin,"です。")
この動画を見る
これは英語、数学、国語の平均点を求めるプログラムである。このプログラムの誤りを指摘し、正しくせよ。
(1)eigo = 50
(2)sugaku = 65
(3)kokugo = 56
(4)heikin = eigo + sugaku + kokugo /3
(5)表示する("平均点は",heikin,"です。")
231-2 変数はラベル!?:箱だけでは表現しきれない部分もスッキリ理解! #shorts
単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計#基本的なプログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
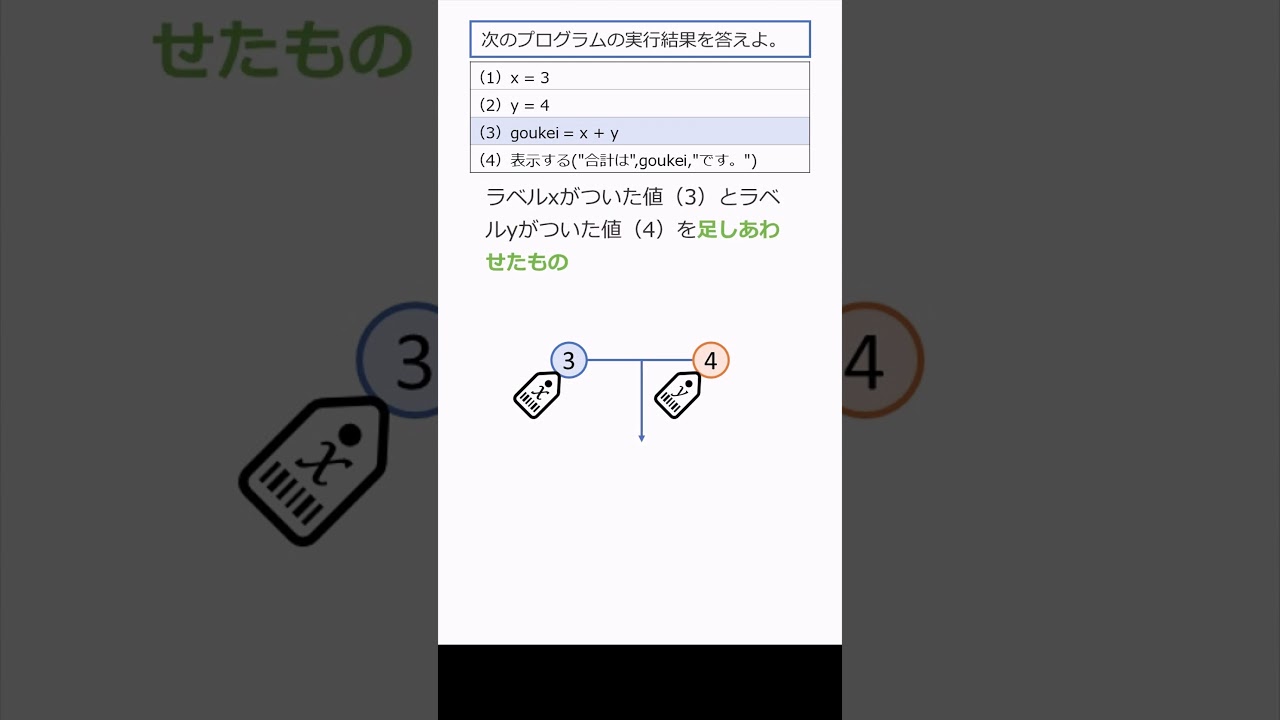
次のプログラムの実行結果を答えよ。
(1)x = 3
(2)y = 4
(3)goukei = x + y
(4)表示する("合計は",goukei,"です。")
この動画を見る
次のプログラムの実行結果を答えよ。
(1)x = 3
(2)y = 4
(3)goukei = x + y
(4)表示する("合計は",goukei,"です。")
231‐1 変数は箱!?:プログラムの第一歩を踏み出そう! #shorts

単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計#基本的なプログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
次のプログラムの実行結果を答えよ。
(1)x = 3
(2)y = 4
(3)goukei = x + y
(4)表示する("合計は",goukei,"です。")
この動画を見る
次のプログラムの実行結果を答えよ。
(1)x = 3
(2)y = 4
(3)goukei = x + y
(4)表示する("合計は",goukei,"です。")
【情報Ⅰ】数値の大きいフローチャートの読み取り #shorts #情報 #フローチャート #模試 #プログラミング
単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計#基本的なプログラミング#探索と整列のプログラム#プログラムによる動的シミュレーション
指導講師:
理数個別チャンネル
問題文全文(内容文):
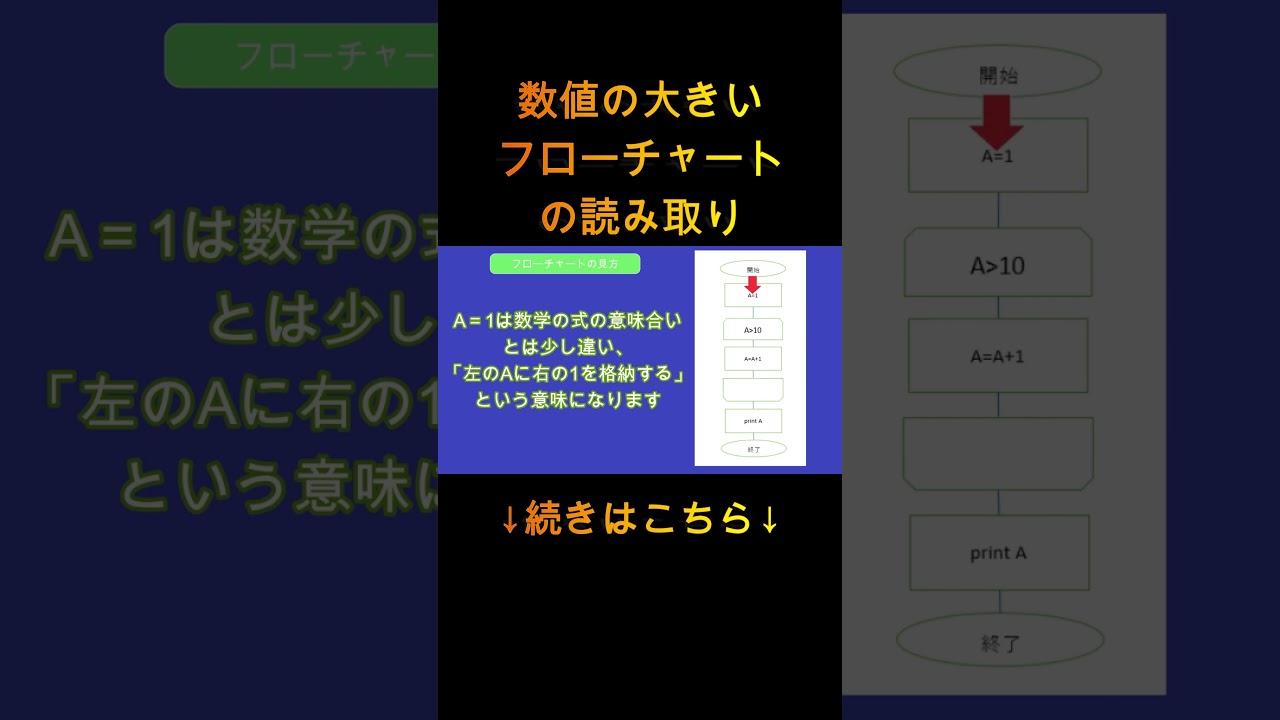
フローチャートの問題、および解説です
数値が大きくなった場合の考え方について学びましょう
この動画を見る
フローチャートの問題、および解説です
数値が大きくなった場合の考え方について学びましょう
