【高校物理】毎日原子9日目【共通テストまで毎日19時投稿】 - 質問解決D.B.（データベース）

　【高校物理】毎日原子9日目【共通テストまで毎日19時投稿】 - 質問解決D.B.（データベース）

質問解決D.B.（データベース） > 動画投稿 > 理科(高校生) > 物理 > 原子 > 【高校物理】毎日原子9日目【共通テストまで毎日19時投稿】

【高校物理】毎日原子9日目【共通テストまで毎日19時投稿】

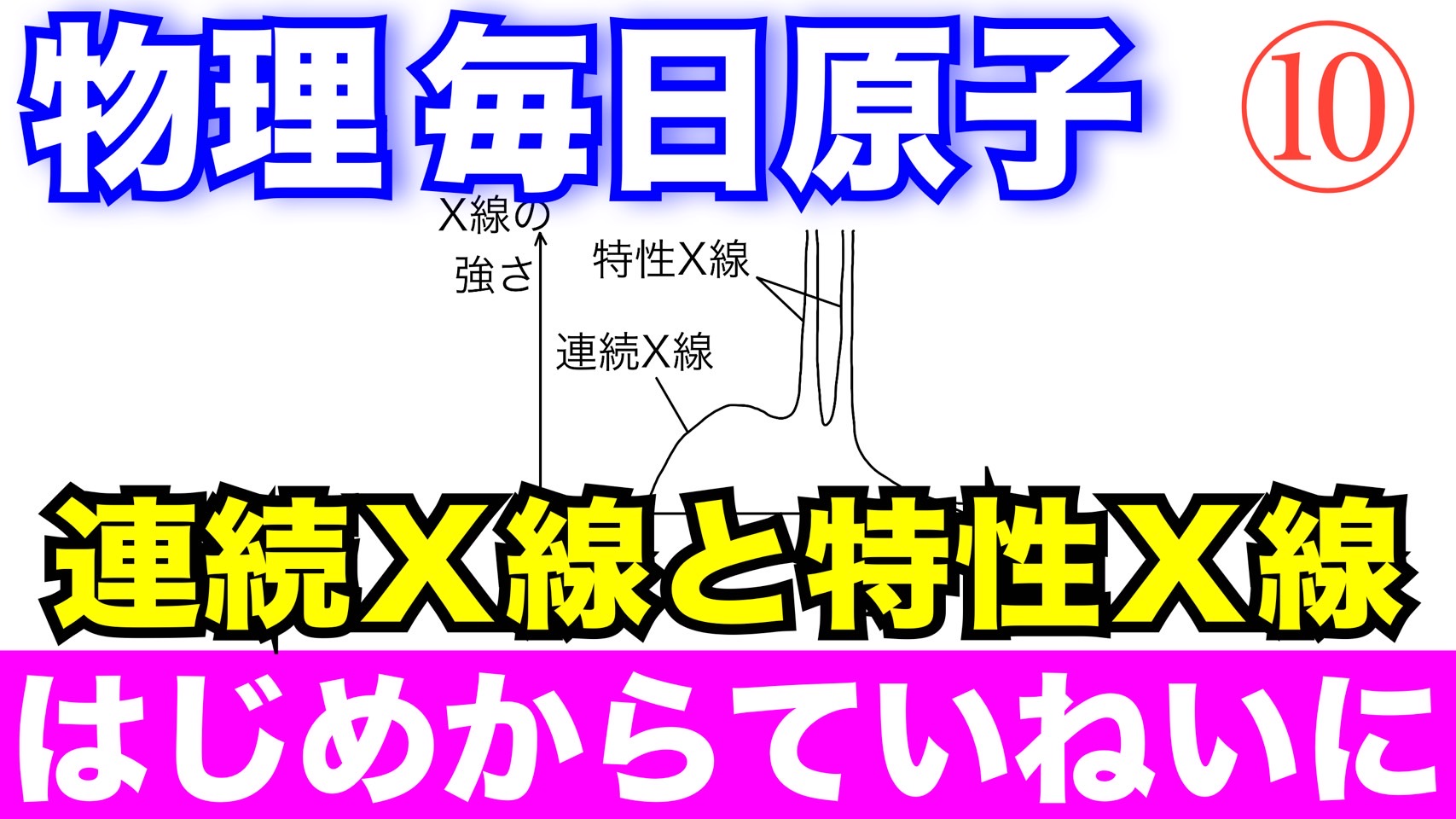
問題文全文(内容文)：
定常状態の水素原子では、質量m、電気量－eの電子が、電気量+eの原子核（陽子）の周りを、半径r、速さvで等速円運動していると考えられる。クーロンの法則の比例定数をkとすると、円運動の式は（１）となる。また、電子は粒子であると同時に、波の性質ももっていて、プランク定数を h とすると、その波長λはλ＝（２）となる。この波動性に対して、ボーアは（３）の条件を満たしていると考えた。ただし、nは自然数とする。以上の関係式からrとnの関係に注目すると、rは（４）に比例し、軌道半径はnによって定まる不連続な値しかとり得ないことがわかった。

チャプター：

0:00 オープニング
0:31 ボーアの原子模型の流れ
5:20 解説開始！
15:07 本日の宿題

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
定常状態の水素原子では、質量m、電気量－eの電子が、電気量+eの原子核（陽子）の周りを、半径r、速さvで等速円運動していると考えられる。クーロンの法則の比例定数をkとすると、円運動の式は（１）となる。また、電子は粒子であると同時に、波の性質ももっていて、プランク定数を h とすると、その波長λはλ＝（２）となる。この波動性に対して、ボーアは（３）の条件を満たしていると考えた。ただし、nは自然数とする。以上の関係式からrとnの関係に注目すると、rは（４）に比例し、軌道半径はnによって定まる不連続な値しかとり得ないことがわかった。

投稿日：2024.01.12

＜シリーズ動画（毎日原子【共通テストまで毎日19時投稿】）＞

【高校物理】毎日原子10日目【共通テストまで毎日19時投稿】

アイキャッチ画像

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
X線管において、初速度0の電子を電圧1.5kVで加速し、陽極金属に衝突させると、X線が発生して、図のようなスペクトルが得られた。電気素量を$1.6×10^{-19}$［C］、プランク定数を$6.6×10^{-34}$［J・s］、真空中の光速を$3.0×10^8$［m/s］とする。次の各問に答えよ。
（1）加速された電子のもつエネルギーは何eVか。
（2）連続X線の最短波長はいくらか。
（3）加速電圧を3倍にしたとき、次の値は何倍になるか。
① 連続X線の最短波長　　　　② 特性X線の波長

宿題
右図は、X線管によって発生したX線のスペクトルである。プランク定数をh、光速をcとする。
（1）右図の①、②に適当な語句を入れよ。
（2）初速度0で陰極を出た電子（電気量−e）を電圧Vで加速し、陰極に当てたとき、陰極から放出されるX線光子の持つ最大エネルギーを求めよ。
（3）（2）のとき、X線の最短波長λ₀はいくらか。
（4） ②Ｘ線の波長をλ₁、λ₂とすると、加速電圧Ｖを大きくしても変化しないのは、λ₀、λ₁、λ₂ のどれか。

この動画を見る　

【高校物理】毎日原子5日目「放射線の進路」の宿題を解いてみた【番外編】

アイキャッチ画像

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
図のように，真空中に放射線源と磁石を配置した。α線，β線，γ線の放射線が放射線源から鉛直上向きに飛び出したとすると，各々の放射線の進路はどのようになるか，図の（a）～（c）から選べ。

この動画を見る　

【高校物理】毎日原子6日目「光電効果」の宿題を解いてみた【番外編】

アイキャッチ画像

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
仕事関数が1.8[eV]の金属の表面に真空中での波長が$4.0×10^{-7}$[m]の光を当てる。真空中の光の速さをc=$3.0×10^8$[m/s]，プランク定数をh=$6.6×10^{-34}$[J・s]，電気素量を$1.6×10^{-19}$[C]とする。この光の光子１個のエネルギーは□.□[eV]である。金属の表面から飛び出した光電子の最大の運動エネルギーは□.□[eV]である。

この動画を見る　

【高校物理】毎日原子8日目【共通テストまで毎日19時投稿】

アイキャッチ画像

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
図のように格子面の間隔（格子定数）が$d$で、原子が規則的に配列している結晶に、波長$λ$の特性$X$線が格子面に対して角$\theta$で入射している。
（1）格子面1、格子面2で反射した２つのX線の経路差を$d、\theta$を用いて表せ。
（2）反射$X$線の強めあう条件を、$d、\theta、λ$、正の数$n（＝1、2、…）$を用いて表せ。
（3） $θ$を0°から大きくしていくと、$\theta＝\theta_0$のとき、はじめて反射$X$線が強めあった。格子定数$d$を、$\theta_0、λ$を用いて表せ。

この動画を見る　

【高校物理】毎日原子３日目「半減期」の宿題を解いてみた【番外編】

アイキャッチ画像

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
古代遺跡から発掘された植物体内の$^{14}C$ の$^{12}C$ に対する割合は，大気中のそれの0.71倍であった。この発掘された植物は今からおよそ何年前に生育していたものと推定されるか。これを有効数字2桁で表すとき，次の式中の空欄ア〜ウに入れる数字として最も適当なものを答えよ。ただし，$^{14}C$ のβ崩壊の半減期は$5.73×10^3$年であり，大気中の$^{14}C$ と$^{12}C$ の割合は常に一定とする。また，$\frac{1}{\sqrt{2}}＝0.71$である。$ □ ．□×10^□$

この動画を見る　

【高校物理】毎日原子7日目【共通テストまで毎日19時投稿】

アイキャッチ画像

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
図のように、波長λ［m］のX線を質量m［kg］の静止している電子に向けて入射したとき、電子は図のθの方向に速さv〔m/s）でたたき出され、入射線はθ’の方向に波長でλ’［m］となって散乱されたとする。プランク定数をh［J・s］、光速をc［m/s］とする。
（1） X線の入射方向の運動量保存則を表せ。
（2） X線の入射方向に垂直な方向の運動量保存則を表せ。
（3）衝突前後のエネルギー保存の法則を表せ。

宿題
真空中に静止していた質量 m［kg］の電子に波長λ［m］のX線光子を衝突させる。
電子はX線の入射方向 θ の角をなす方向に速さ v［m/s］ではね飛ばされ、X線光子は
入射方向と垂直な方向に波長λ’［m］となって散乱された。光速をc［m/s］、プラ
ンク定数をh［J・s］とする。
（１）衝突前後のエネルギー保存則を表せ。
（２）X線の入射方向に関する運動量保存則を表せ。
（３）X線の入射方向に垂直な方向に関する運動量保存則を表せ。

この動画を見る　

【高校物理】毎日原子6日目【共通テストまで毎日19時投稿】

アイキャッチ画像

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
仕事関数が2.0[eV]の金属の表面に波長$4.0×10^{-7}$[m]の光を当てた。プランク定数をh=$6.6×10^{-34}$[J・s]、真空中の光の速さをc=$3.0×10^8$[m/s]、電気素量を$1.6×10^{-19}$[C]とする。金属の表面から飛び出してくる電子の運動エネルギーの最大値は□.□[eV]である。

宿題
仕事関数が1.8[eV]の金属の表面に真空中での波長が$4.0×10^{-7}$[m]の光を当てる。真空中の光の速さをc=$3.0×10^8$[m/s]，プランク定数をh=$6.6×10^{-34}$[J・s]，電気素量を$1.6×10^{-19}$[C]とする。この光の光子１個のエネルギーは□.□[eV]である。金属の表面から飛び出した光電子の最大の運動エネルギーは□.□[eV]である。

この動画を見る　

【高校物理】毎日原子5日目【共通テストまで毎日19時投稿】

アイキャッチ画像

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
α線，β線，γ線すべてを含む放射線に，図に示す向きに電場Eを加えた。このときのα線，β線，γ線各々の進路を図の（ア）～（ウ）の中から選べ。

宿題
図のように，真空中に放射線源と磁石を配置した。α線，β線，γ線の放射線が放射線源から鉛直上向きに飛び出したとすると，各々の放射線の進路はどのようになるか，図の（a）～（c）から選べ。

この動画を見る　

【高校物理】毎日原子4日目【共通テストまで毎日19時投稿】

アイキャッチ画像

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
核融合反応 $_1^2H+ _1^2H→_Z^AX + _1^1H$で得られる原子核Xの質量数Aと原子番号Zはそれぞれ□と□である□と□の核子1個当たりの結合エネルギーをそれぞれ1.1 MeVと2.8MeVとすると，この反応で放出されるエネルギーは□．□MeV となる。

宿題
$^2H$と$^3H$の原子核が反応して$^4He$と中性子ができた。$^2H$，$^3H$，$^4He$の核子1個あたりの結合エネルギーは，それぞれ1.1MeV，2.8MeV，7.1MeVである。この反応で解放されるエネルギーは□MeVである。

この動画を見る　

【高校物理】毎日原子3日目【共通テストまで毎日19時投稿】

アイキャッチ画像

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
$_{239}$Puは半減期$2.4×10^4$〔年〕で崩壊する放射性物質である。崩壊せずに残っている$_{239}$Puの量がもとの10%になるまでに要する年数ｔを有効数字2桁で表せ。ただし、$log_{10}2＝0.30$とする。

宿題
古代遺跡から発掘された植物体内の$^{14}$Cの$^{12}$Cに対する割合は，大気中のそれの0.71倍であった。この発掘された植物は今からおよそ何年前に生育していたものと推定されるか。これを有効数字2桁で表すとき，次の式中の空欄ア〜ウに入れる数字として最も適当なものを答えよ。ただし，$^{14}$Cのβ崩壊の半減期は$5.73×10^3$年であり，大気中の$^{14}$Cと$^{12}$Cの割合は常に一定とする。また，$\frac{1}{\sqrt{2}}＝0.71$である。 $□ ．□×10^□$

この動画を見る　

【高校物理】毎日原子2日目【共通テストまで毎日19時投稿】

アイキャッチ画像

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
次のような反応で原子核Xが生成された。
$_{92}^{235}$U+$_0^1$n→$_{42}^{103}$Mo+X+2$_0^1$n
原子核Xの原子番号は□、中性子数は□、質量数は□である。

【宿題】
核反応$_2^4$He+$_{13}^{27}$Al→X+$_0^1$nで得られる原子核Xの質量数と原子番号と中性子数はそれぞれ□、□、□である。

この動画を見る　

【高校物理】毎日原子1日目【共通テストまで毎日19時投稿】

アイキャッチ画像

単元： #物理#大学入試過去問(物理)#理科(高校生)#原子

指導講師：理数個別チャンネル

問題文全文(内容文)：
ウラン原子核$_{92}^{235}$Uは$\alpha$崩壊を□回、$\beta$崩壊を□回おこない鉛原子核$_{82}^{207}$Pbへと崩壊する。
【宿題】
$_{92}^{238}$Uは$_{86}^{218}$Rnになるまでに$\alpha$崩壊を□回、$\beta$崩壊を□回行う。

この動画を見る　

PAGE TOP