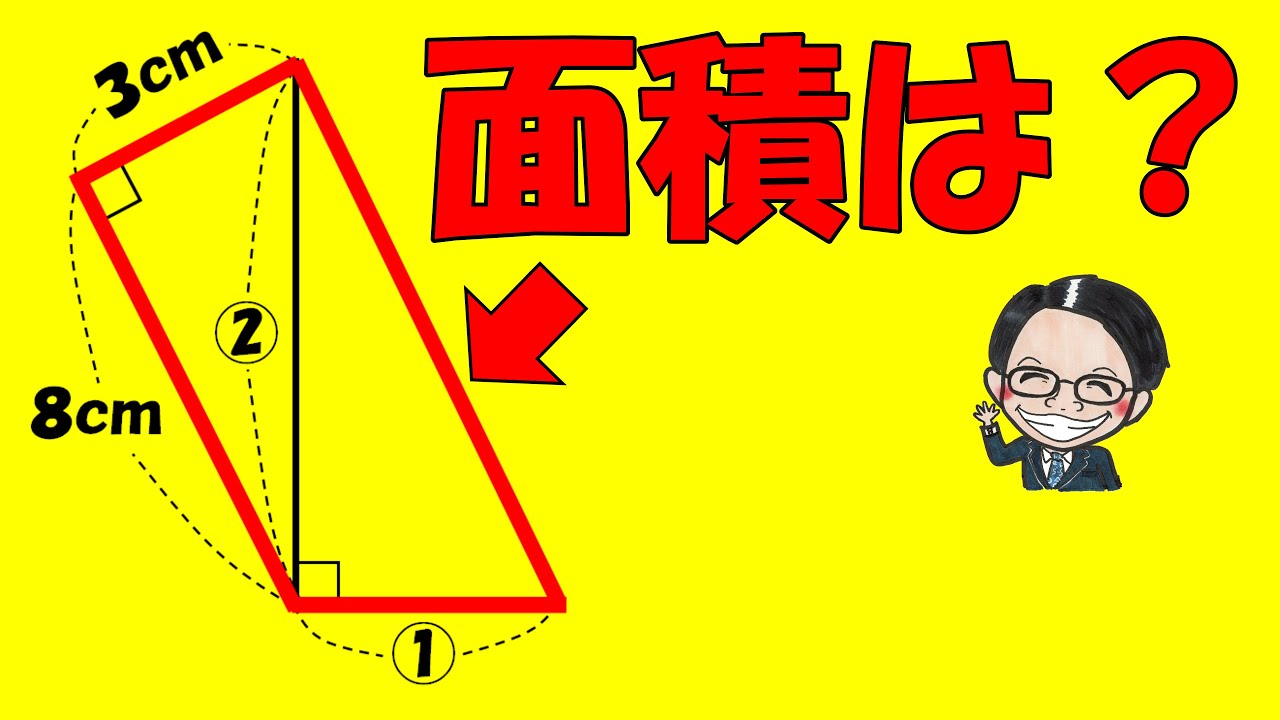
問題文全文(内容文):
小4 算数 わり算の筆算③ (472÷15)
以下の問に答えよ
$\begin{array}{rrrrrr}
①&21\enclose{longdiv}{169\phantom{0}} &
②&51\enclose{longdiv}{355\phantom{0}} &
③&23\enclose{longdiv}{182\phantom{0}} \\
④&16\enclose{longdiv}{130\phantom{0}} &
⑤&15\enclose{longdiv}{472\phantom{0}} &
⑥&23\enclose{longdiv}{652\phantom{0}} \\
\end{array}$
※図は動画内参照
小4 算数 わり算の筆算③ (472÷15)
以下の問に答えよ
$\begin{array}{rrrrrr}
①&21\enclose{longdiv}{169\phantom{0}} &
②&51\enclose{longdiv}{355\phantom{0}} &
③&23\enclose{longdiv}{182\phantom{0}} \\
④&16\enclose{longdiv}{130\phantom{0}} &
⑤&15\enclose{longdiv}{472\phantom{0}} &
⑥&23\enclose{longdiv}{652\phantom{0}} \\
\end{array}$
※図は動画内参照
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
小4 算数 わり算の筆算③ (472÷15)
以下の問に答えよ
$\begin{array}{rrrrrr}
①&21\enclose{longdiv}{169\phantom{0}} &
②&51\enclose{longdiv}{355\phantom{0}} &
③&23\enclose{longdiv}{182\phantom{0}} \\
④&16\enclose{longdiv}{130\phantom{0}} &
⑤&15\enclose{longdiv}{472\phantom{0}} &
⑥&23\enclose{longdiv}{652\phantom{0}} \\
\end{array}$
※図は動画内参照
小4 算数 わり算の筆算③ (472÷15)
以下の問に答えよ
$\begin{array}{rrrrrr}
①&21\enclose{longdiv}{169\phantom{0}} &
②&51\enclose{longdiv}{355\phantom{0}} &
③&23\enclose{longdiv}{182\phantom{0}} \\
④&16\enclose{longdiv}{130\phantom{0}} &
⑤&15\enclose{longdiv}{472\phantom{0}} &
⑥&23\enclose{longdiv}{652\phantom{0}} \\
\end{array}$
※図は動画内参照
投稿日:2012.09.13