【中学受験問題に挑戦】97 （”大人”は頭の体操） 三角形の中におうぎ形（面積問題） - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 平面図形 > 【中学受験問題に挑戦】97　（”大人”は頭の体操）　三角形の中におうぎ形（面積問題）

【中学受験問題に挑戦】97　（”大人”は頭の体操）　三角形の中におうぎ形（面積問題）

問題文全文(内容文)：
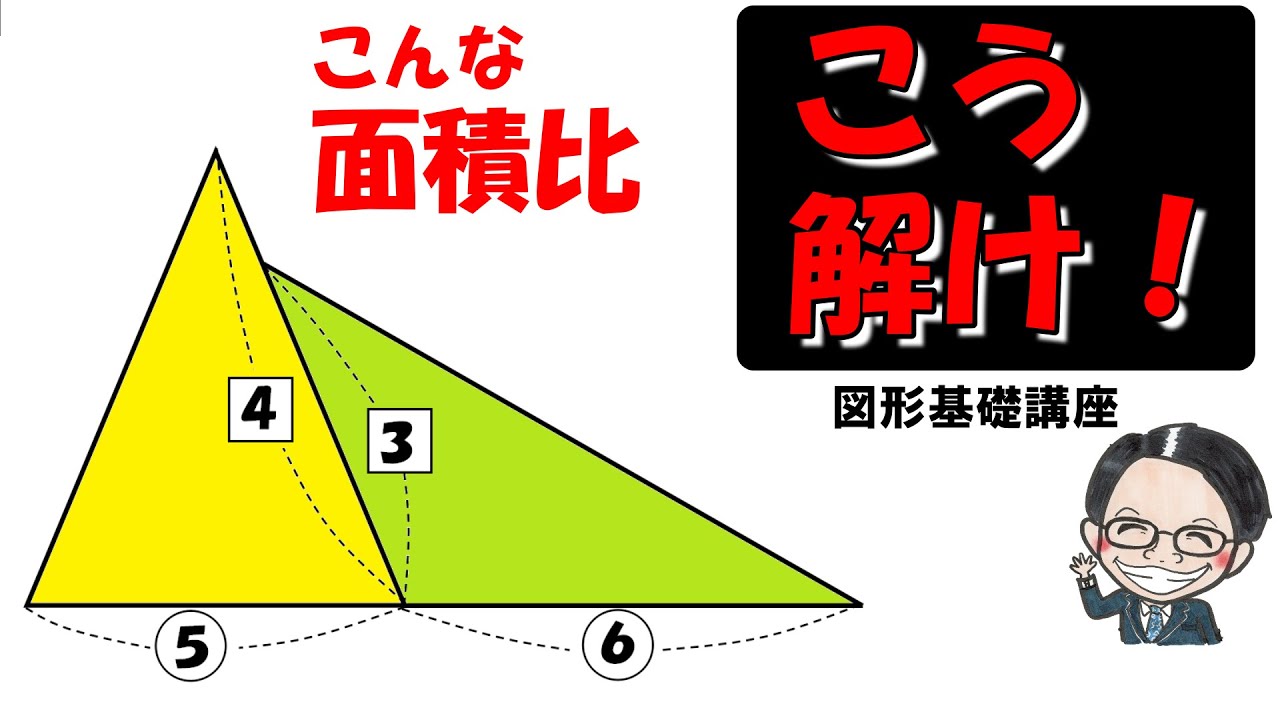
緑色の部分の面積を求めよ。
三角形とおうぎ形2つを組み合わせ、
AM=BMは対等です。

※上記は辺の長さの関係です。
※円周率=3.14

※図は動画内参照
単元： #算数(中学受験)#平面図形
指導講師： 算数・数学ちゃんねる
問題文全文(内容文)：
緑色の部分の面積を求めよ。
三角形とおうぎ形2つを組み合わせ、
AM=BMは対等です。

※上記は辺の長さの関係です。
※円周率=3.14

※図は動画内参照
投稿日：2024.03.20

＜関連動画＞

小学生で解ける図の面積を求めよ～三平方の定理禁止～【ジュニア算数オリンピック】

アイキャッチ画像
単元： #算数(中学受験)#算数オリンピック
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
三平方の定理を使わずに面積を求めよ
この動画を見る　

○○を知っていればすぐ解ける！定番テクニックが生きる素晴らしい１題！【中学受験算数】【オリジナル問題】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： こばちゃん塾
問題文全文(内容文)：
下図のxは何度？（図は正確とは限りません）
＊図は動画内参照
この動画を見る　

2023年東邦大学付属東邦中学校算数「相似、面積」

アイキャッチ画像
単元： #算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#東邦大学付属東邦中学
指導講師： 重吉
問題文全文(内容文)：
2023年東邦大学付属東邦中学校算数「相似、面積」
長方形があり、影がついた部分の面積を求めよ。
※動画内の図を参照
この動画を見る　

中学受験算数「約数と公約数③（素数と素因数分解）」小学４年生～６年生対象【毎日配信】

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
指導講師： 中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
第20回約数と公約数③ (素数と素因数分解)

例1
次の整数を素因数分解しなさい。

(1) 24

(2) 63

(3) 160

例2
1から25までの整数について、次の問いに答えなさい。

(1)約数が2個の整数は、何個ありますか。

(2)約数が3個の整数は、何個ありますか。

(3)約数が奇数個の整数は何個ありますか。
この動画を見る　

【SAPIX小5算数51-24】仕事算(B1)：途中で休む【デイリーサポート確認編】

アイキャッチ画像
単元： #算数(中学受験)#文章題#仕事算とニュートン算
教材： #SPX#5年算数D-支援#中学受験教材
指導講師： 受験算数の森
問題文全文(内容文)：
ともみさんなら9日で、まいさんなら15日で仕上げる仕事があります。この仕事を2人で一緒に始めましたが、途中でともみさんが何日か休んだため、この仕事を仕上げるのに10日かかりました。ともみさんが休んだのは何日ですか。
この動画を見る　
PAGE TOP