中学１年生で勉強する資料の分析を１本の動画にまとめてみました【新学習指導要領】

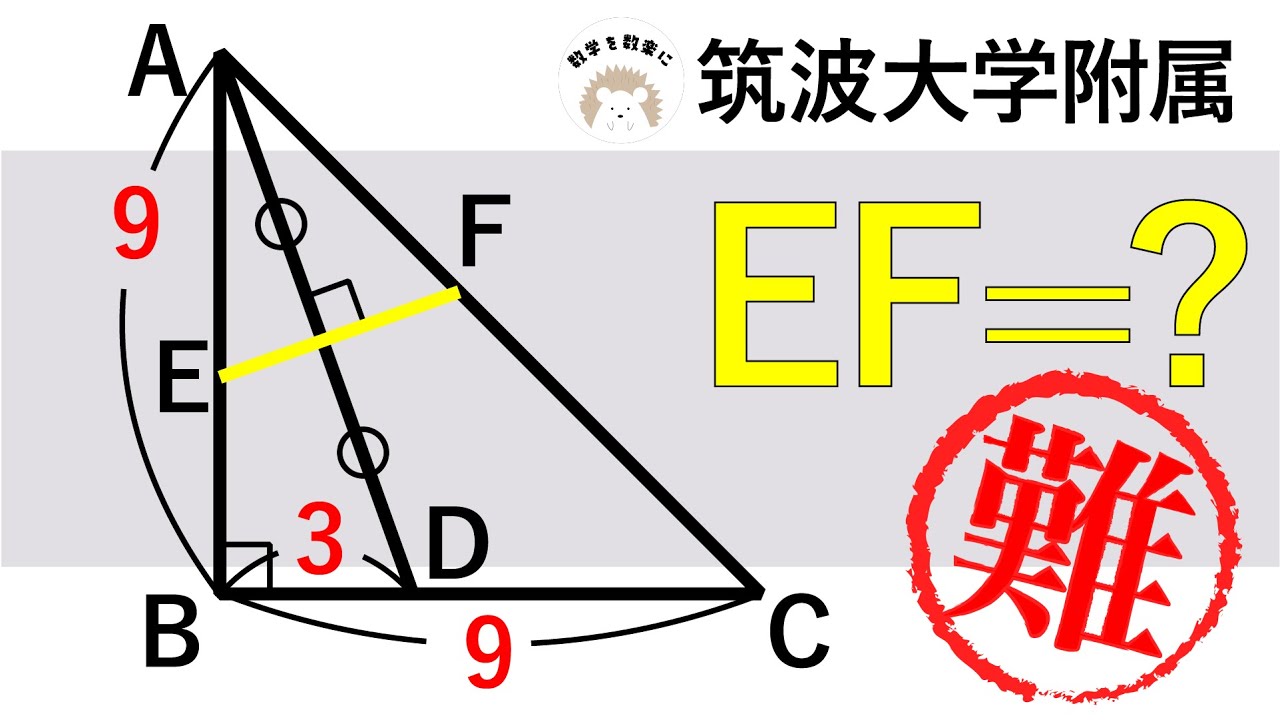
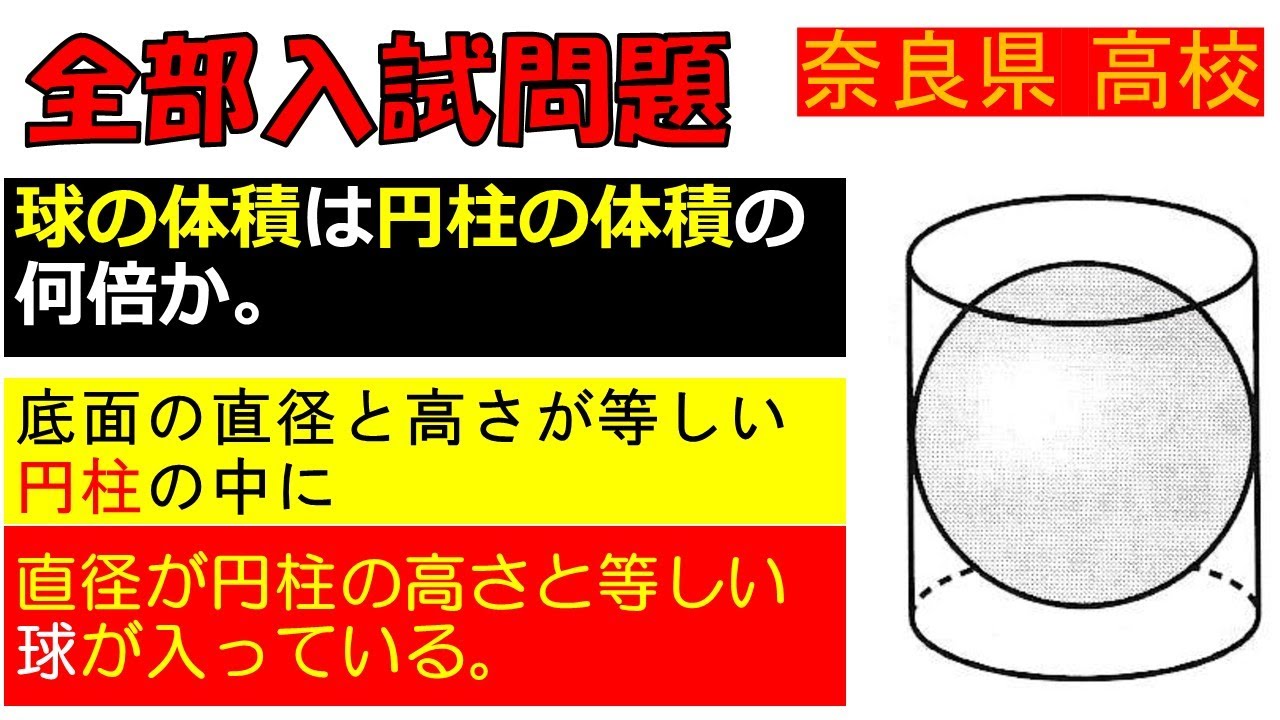
問題文全文(内容文)：
資料の分析と活用のまとめ

右の表1を(①)表という。　※表は動画参照
資料を整理するために用いる区間を(②)
区間の幅を(③)、(➁)の真ん中の値を(④)、その(➁)に入っている資料の個数を(⑤)といい
その(➁)に入っている資料の個数を(⑤)といい、(⑤)の合計に対する割合を(⑥)という。

また、表2のような柱状グラフを(⑦)といい、
それぞれの長方形の上の辺の中点を結んだものを(⑧)線という。

単元： #数学(中学生)#中１数学#資料の活用

指導講師：とある男が授業をしてみた

投稿日：2020.03.19

＜関連動画＞

文字式のイメージはどう？

単元： #数学(中学生)#中１数学#文字と式

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
下記質問の解説動画です
文字式の計算が分からないです
$a+b+c=?$

この動画を見る　

中学受験解き方は高校受験の解き方より難しい

単元： #算数(中学受験)#数学(中学生)#中１数学#平面図形#平面図形その他#平面図形

指導講師：数学を数楽に

問題文全文(内容文)：
$x=?$

この動画を見る　

【中１　数学】　　１－①⑦　文字の計算（加法・減法）

単元： #数学(中学生)#中１数学#文字と式

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
中1 数学　文字の計算（加法・減法）
左の式から右の式を～
（例）$5x-3$ 、 $2x+7$
足すと…
$5x-3+2x+7$
引くと…
$5x-3-(2x+7)$

次の計算をせよ
① $-5x+2x=$
② $-5a-3a=$
③ $x-\dfrac{1}{3}x=$
④ $5x-2+3x=$
⑤ $-7x-x+2y+3y=$
⑥ $+9x-5x^2-3x=$

この動画を見る　

中１数学「四則の混じった文字式の表し方①」【毎日配信】

単元： #数学(中学生)#中１数学#文字と式

指導講師：中学受験算数・高校受験数学けいたくチャンネル

問題文全文(内容文)：
四則の混じった文字式の表し方①に関して解説していきます。

この動画を見る　

【中1 数学】中1-34 方程式の利用あわせて編

単元： #数学(中学生)#中１数学#方程式

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
①150円の梨と120円の桃を合わせて15個買うと、2070円でした。
梨と桃をそれぞれ何個買ったかな？

②370円のケーキと180円のプリンを合わせて8個買い、150円に箱に入れてもらうと、全部で2160円でした。
ケーキとプリンをそれぞれ何個買ったかな？

③とある中学生の人数は、男女合わせて450人で、男子は女子より16人少ない。
男子と女子の人数は何人？

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 中学１年生で勉強する資料の分析を１本の動画にまとめてみました【新学習指導要領】

＜関連動画＞

文字式のイメージはどう？

中学受験解き方は高校受験の解き方より難しい

【中１ 数学】 １－①⑦ 文字の計算（加法・減法）

中１数学「四則の混じった文字式の表し方①」【毎日配信】

【中1 数学】中1-34 方程式の利用 あわせて編