問題文全文(内容文):
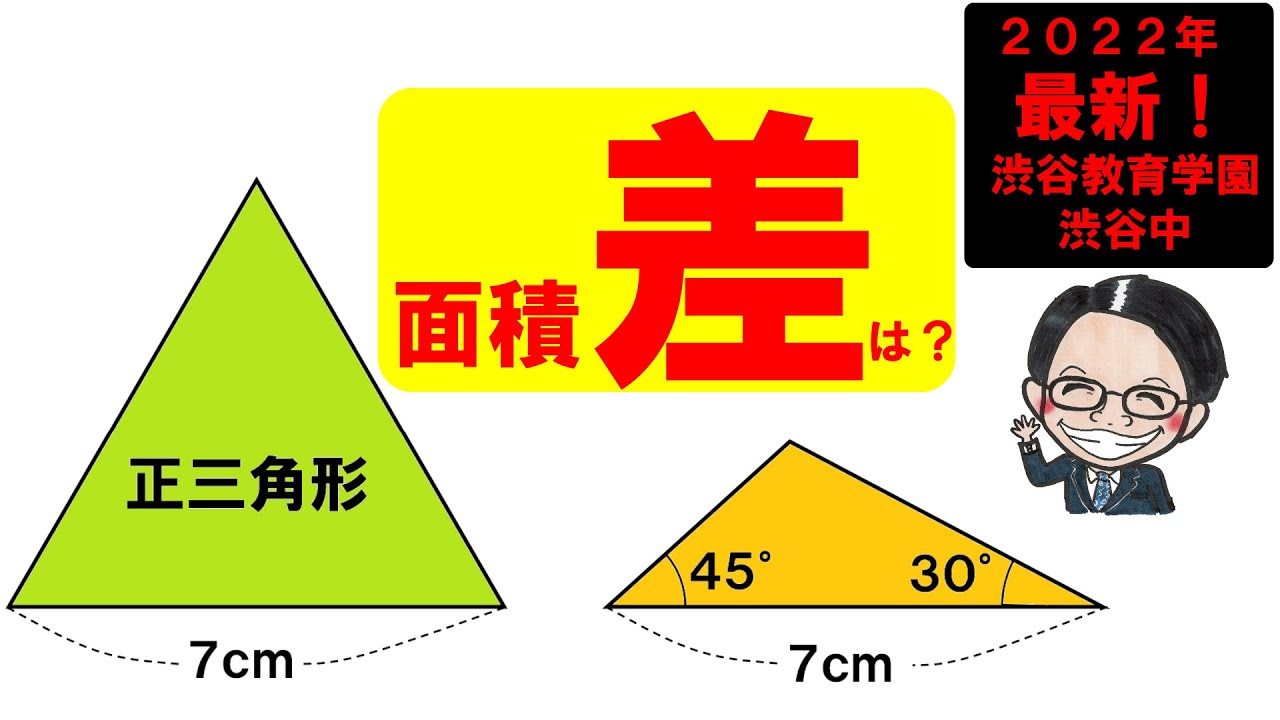
右図の三角形ABCにおいて、AB=12cm、AC=9cmです。AB,AC上に点D,EをそれぞれAD=8.1cm、AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、BEとCDの交点をFとします。次の問いに答えなさい。
(3)三角形ABCの面積は、三角形CEFの面積の何倍ですか。
右図の三角形ABCにおいて、AB=12cm、AC=9cmです。AB,AC上に点D,EをそれぞれAD=8.1cm、AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、BEとCDの交点をFとします。次の問いに答えなさい。
(3)三角形ABCの面積は、三角形CEFの面積の何倍ですか。
チャプター:
00:00 オープニング
00:05 問題解説
03:00 エンディング
単元:
#算数(中学受験)#平面図形#平面図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図の三角形ABCにおいて、AB=12cm、AC=9cmです。AB,AC上に点D,EをそれぞれAD=8.1cm、AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、BEとCDの交点をFとします。次の問いに答えなさい。
(3)三角形ABCの面積は、三角形CEFの面積の何倍ですか。
右図の三角形ABCにおいて、AB=12cm、AC=9cmです。AB,AC上に点D,EをそれぞれAD=8.1cm、AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、BEとCDの交点をFとします。次の問いに答えなさい。
(3)三角形ABCの面積は、三角形CEFの面積の何倍ですか。
投稿日:2022.09.25