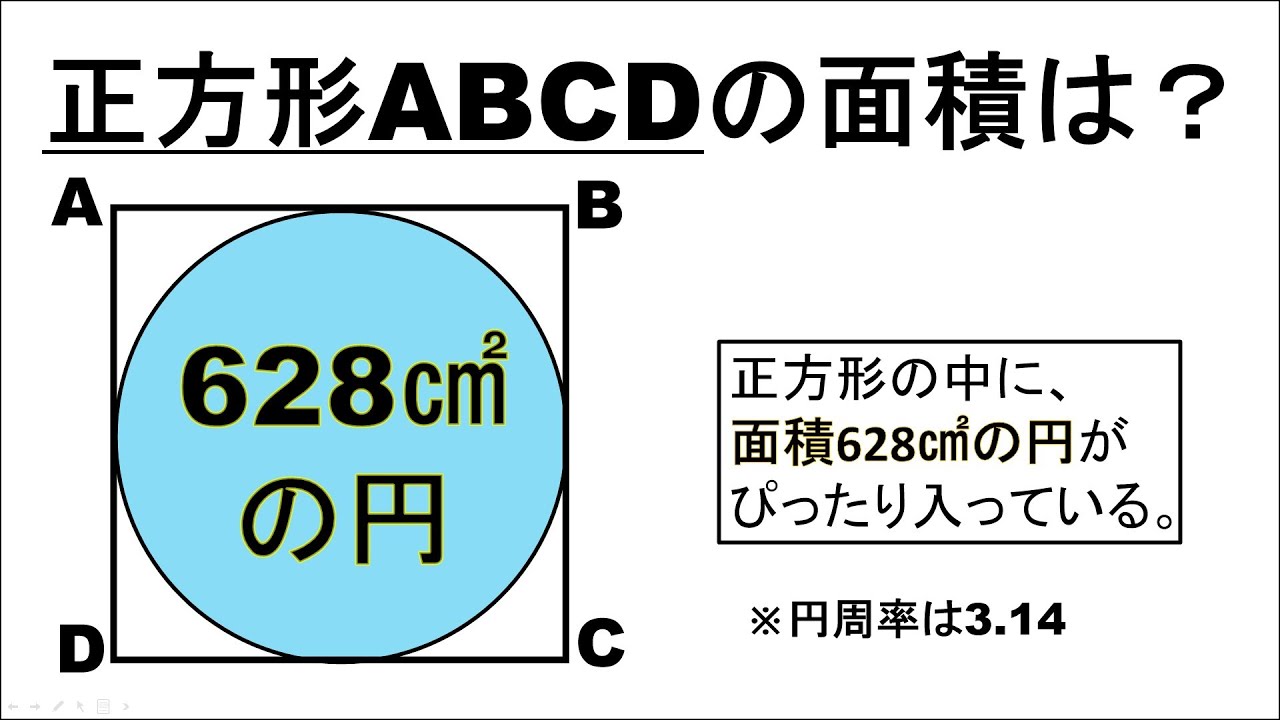
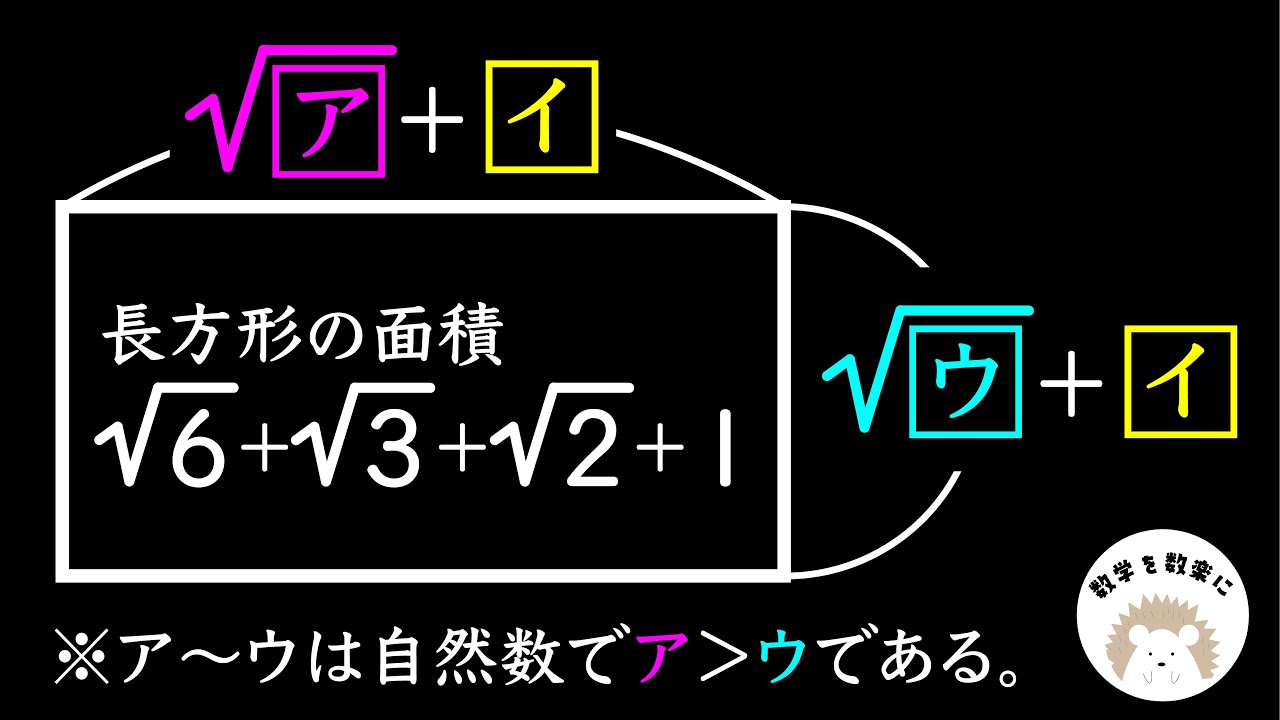
問題文全文(内容文):
大問1
(2)2桁の整数A、Bがあります。AとBの最大公約数は6、最小公倍数は360です。AはBより大きいとき、Aにあてはまる数をすべて求めなさい。
(3) 500円硬貨,100円硬貨,50円硬貨がたくさんあります。これらの硬貨を使って1600円を支払う
方法は何通りありますか。ただし、使わない硬貨があってもよいものとします。
(4) ある学校の入学試験の合格者は受験者全体の40%で、合格者の平均点は合格最低点より12点高く、不合格者の平均点は合格最低点より13点低かったです。また、受験者全体の平均点は60点でした。このとき、合格最低点を求めなさい。
大問1
(2)2桁の整数A、Bがあります。AとBの最大公約数は6、最小公倍数は360です。AはBより大きいとき、Aにあてはまる数をすべて求めなさい。
(3) 500円硬貨,100円硬貨,50円硬貨がたくさんあります。これらの硬貨を使って1600円を支払う
方法は何通りありますか。ただし、使わない硬貨があってもよいものとします。
(4) ある学校の入学試験の合格者は受験者全体の40%で、合格者の平均点は合格最低点より12点高く、不合格者の平均点は合格最低点より13点低かったです。また、受験者全体の平均点は60点でした。このとき、合格最低点を求めなさい。
単元:
#算数(中学受験)#過去問解説(学校別)#早稲田実業中等部
指導講師:
重吉
問題文全文(内容文):
大問1
(2)2桁の整数A、Bがあります。AとBの最大公約数は6、最小公倍数は360です。AはBより大きいとき、Aにあてはまる数をすべて求めなさい。
(3) 500円硬貨,100円硬貨,50円硬貨がたくさんあります。これらの硬貨を使って1600円を支払う
方法は何通りありますか。ただし、使わない硬貨があってもよいものとします。
(4) ある学校の入学試験の合格者は受験者全体の40%で、合格者の平均点は合格最低点より12点高く、不合格者の平均点は合格最低点より13点低かったです。また、受験者全体の平均点は60点でした。このとき、合格最低点を求めなさい。
大問1
(2)2桁の整数A、Bがあります。AとBの最大公約数は6、最小公倍数は360です。AはBより大きいとき、Aにあてはまる数をすべて求めなさい。
(3) 500円硬貨,100円硬貨,50円硬貨がたくさんあります。これらの硬貨を使って1600円を支払う
方法は何通りありますか。ただし、使わない硬貨があってもよいものとします。
(4) ある学校の入学試験の合格者は受験者全体の40%で、合格者の平均点は合格最低点より12点高く、不合格者の平均点は合格最低点より13点低かったです。また、受験者全体の平均点は60点でした。このとき、合格最低点を求めなさい。
投稿日:2025.02.14