 過去問解説(学校別)
過去問解説(学校別)
 過去問解説(学校別)
過去問解説(学校別)
福田のおもしろ数学057〜灘中学の問題〜展開図を見て体積を求めよう
単元:
#算数(中学受験)#過去問解説(学校別)#灘中学校
指導講師:
福田次郎
問題文全文(内容文):
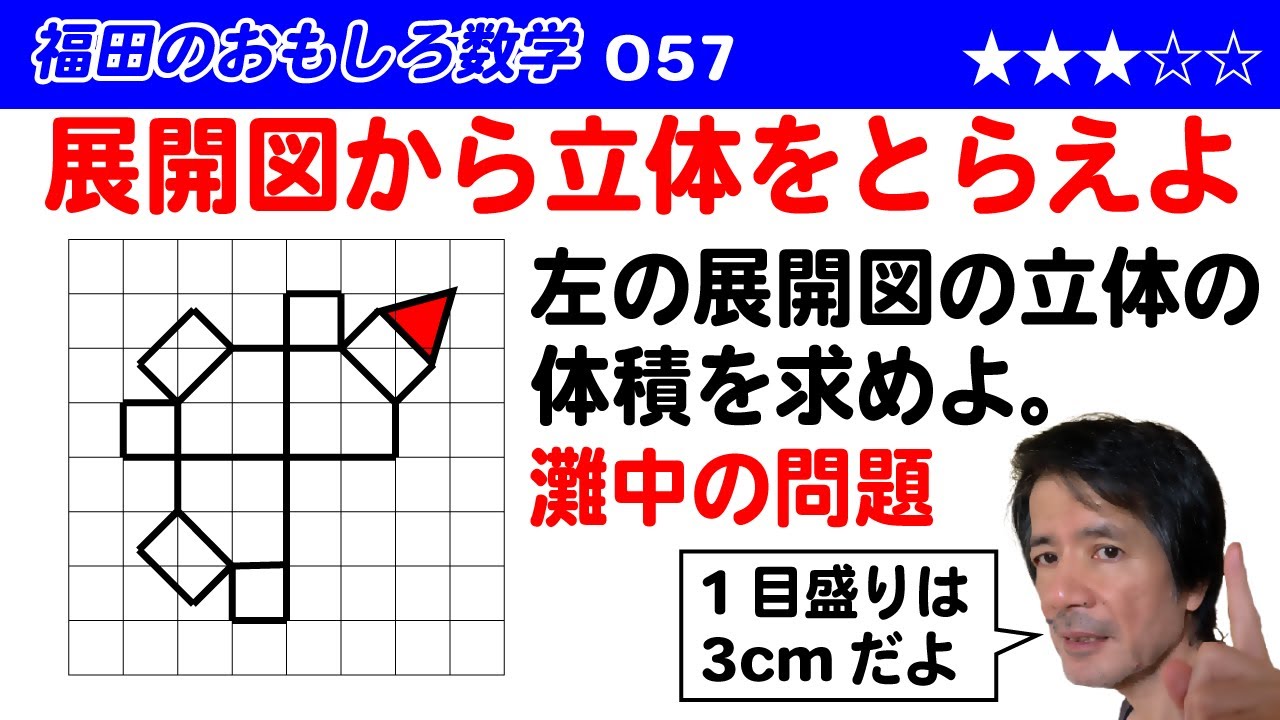
ある立体の展開図を、幅が 3cm の方眼紙にかくと、次の図のようになった。斜線をつけた三角形は正三角形である。また正方形でない四角形の面はすべて長方形である。この立体の体積を求めよ。
※図は動画内参照
この動画を見る
ある立体の展開図を、幅が 3cm の方眼紙にかくと、次の図のようになった。斜線をつけた三角形は正三角形である。また正方形でない四角形の面はすべて長方形である。この立体の体積を求めよ。
※図は動画内参照
【2024年神戸女学院中(算数)】平面図形の問題
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#神戸女学院中学
指導講師:
受験算数の森
問題文全文(内容文):
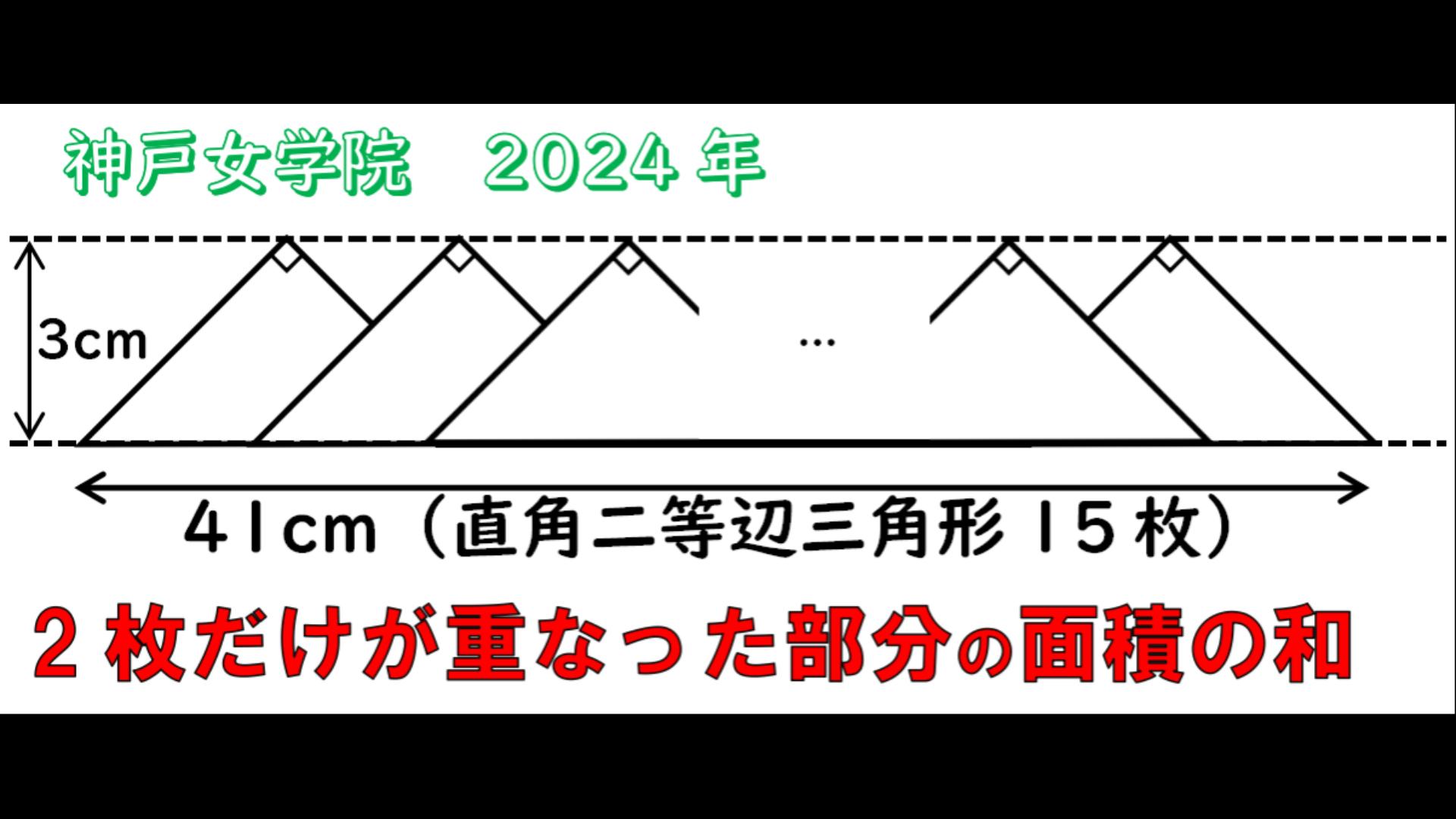
同じ大きさの直角二等辺三角形を並べます。図のように15枚を等間隔に並べたとき、2枚だけが重なった部分の面積の和を求めなさい。
この動画を見る
同じ大きさの直角二等辺三角形を並べます。図のように15枚を等間隔に並べたとき、2枚だけが重なった部分の面積の和を求めなさい。
【2024年渋谷幕張中(算数)】平面図形の問題
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#渋谷教育学園幕張中学校
指導講師:
受験算数の森
問題文全文(内容文):
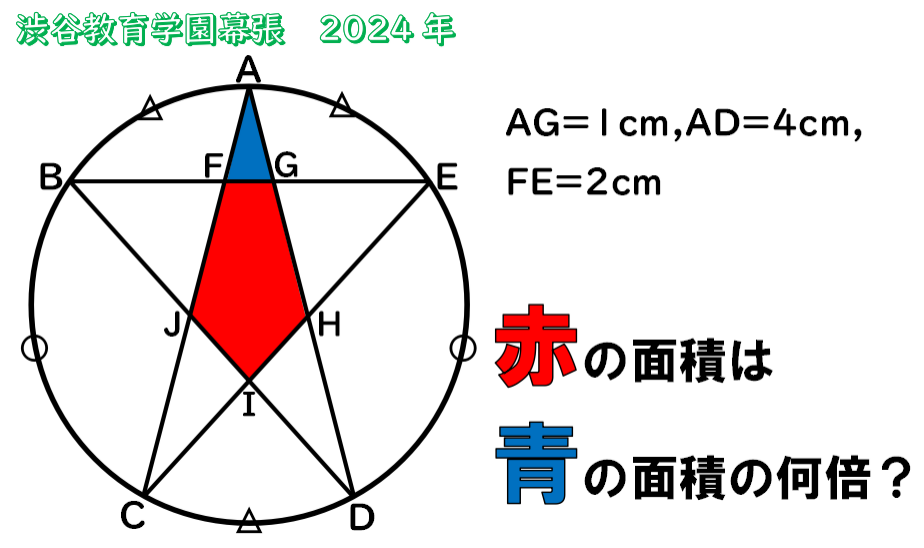
図のように、円周を5つの点A,B,C,D,Eで区切ったとき、△をつけた3つの曲線部分AB,CD,AEの長さは等しく、〇をつけた2つの曲線部分BC,DEの長さは等しくなりました。また、直線AGの長さは1cm、直線ADの長さは4cm、直線FEの長さは2cmです。次の問いに答えなさい。
(1)直線FGの長さは何cmですか。
(2)直線HIと直線ICの長さの比を、最も簡単な整数の比で答えなさい。
(3)五角形FGHIJの面積は、三角形AFGの面積の何倍ですか。
この動画を見る
図のように、円周を5つの点A,B,C,D,Eで区切ったとき、△をつけた3つの曲線部分AB,CD,AEの長さは等しく、〇をつけた2つの曲線部分BC,DEの長さは等しくなりました。また、直線AGの長さは1cm、直線ADの長さは4cm、直線FEの長さは2cmです。次の問いに答えなさい。
(1)直線FGの長さは何cmですか。
(2)直線HIと直線ICの長さの比を、最も簡単な整数の比で答えなさい。
(3)五角形FGHIJの面積は、三角形AFGの面積の何倍ですか。
【受験算数】慶應義塾中等部2018第3問(3)

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#慶應義塾中等部
指導講師:
理数個別チャンネル
問題文全文(内容文):
1辺の長さがそれぞれ21cmと27cmの正三角形が重なってできる六角形に色をつけました。色をつけた六角形の向かい合う辺がそれぞれ平行の時、色をつけた六角形の周りの長さは▢cmである。
この動画を見る
1辺の長さがそれぞれ21cmと27cmの正三角形が重なってできる六角形に色をつけました。色をつけた六角形の向かい合う辺がそれぞれ平行の時、色をつけた六角形の周りの長さは▢cmである。
【受験算数】慶應義塾中等部2018第3問(1)

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#慶應義塾中等部
指導講師:
理数個別チャンネル
問題文全文(内容文):
長方形を対角線で折り返しました。角アと角イが8:5である時、角Xの大きさは▢°である。
この動画を見る
長方形を対角線で折り返しました。角アと角イが8:5である時、角Xの大きさは▢°である。
【受験算数】早稲田中学校 2019年(第1回)大問2(2)図形問題台形とおうぎ形
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#早稲田中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
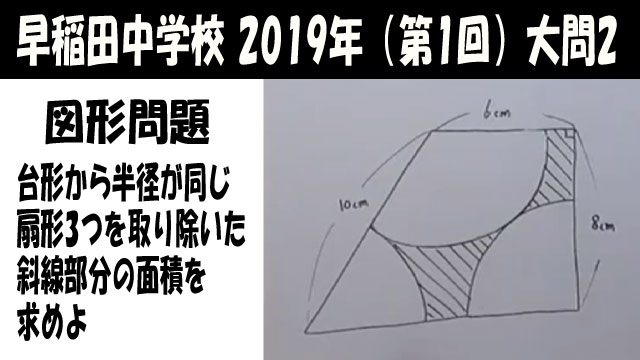
台形から半径が同じ扇形3つを取り除いた斜線部分の面積を求めよ
この動画を見る
台形から半径が同じ扇形3つを取り除いた斜線部分の面積を求めよ
【受験算数】神奈川大学附属2022B日程過去問売買損益

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#神奈川大学附属中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
りんご1個80円でいくつか仕入れ、3600円の利益を見込んで定価をつけて売り始めました。しかし、そのうちの10個が売れ残ったため、実際の利益は2400円となった。このとき定価は何円ですか。
この動画を見る
りんご1個80円でいくつか仕入れ、3600円の利益を見込んで定価をつけて売り始めました。しかし、そのうちの10個が売れ残ったため、実際の利益は2400円となった。このとき定価は何円ですか。
【受験算数】『聖光の2022年入試問題【場合の数】を丁寧に解いてみた』

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#聖光学院中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
1~5までの数字が書かれた赤・白・青の3色の玉が1個ずつ合計15個あります。
(1)15個の玉の中から5個の玉を選んで一列に並べる並べ方のうち、左から順に赤・赤・白・白・白と並ぶような玉の並べ方は全部で何通りありますか?
(2)15個の玉の中から3個の玉を選んで一列に並べます。玉に書かれた数字を左から百の位・十の位・一の位として3桁の数字を作る時、
【ア】3桁の数字が144となるような玉の並べ方は全部で何通りありますか?
【イ】3桁の数字が18の倍数となるような玉の並べ方は全部で何通りありますか?
(3)15個の玉の中から4個の玉を選んで一列に並べ、玉に書かれた数字を左から千の位・百の位・十の位・一の位として4桁の数を作ることを考えます。今、ある4個の玉を選んだところ、それぞれの並べ方から作られる数の総和は106656となりました。玉に書かれている4つの数字の組み合わせとして考えられるものを全て答えなさい。
この動画を見る
1~5までの数字が書かれた赤・白・青の3色の玉が1個ずつ合計15個あります。
(1)15個の玉の中から5個の玉を選んで一列に並べる並べ方のうち、左から順に赤・赤・白・白・白と並ぶような玉の並べ方は全部で何通りありますか?
(2)15個の玉の中から3個の玉を選んで一列に並べます。玉に書かれた数字を左から百の位・十の位・一の位として3桁の数字を作る時、
【ア】3桁の数字が144となるような玉の並べ方は全部で何通りありますか?
【イ】3桁の数字が18の倍数となるような玉の並べ方は全部で何通りありますか?
(3)15個の玉の中から4個の玉を選んで一列に並べ、玉に書かれた数字を左から千の位・百の位・十の位・一の位として4桁の数を作ることを考えます。今、ある4個の玉を選んだところ、それぞれの並べ方から作られる数の総和は106656となりました。玉に書かれている4つの数字の組み合わせとして考えられるものを全て答えなさい。
【中学受験算数】『渋渋の2022年入試の良問を丁寧に解説してみた』

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#渋谷教育学園渋谷中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
渋谷教育学園渋谷中2022入試問題大問3
(1)頂角30度、等辺の長さが5cmの二等辺三角形の面積はいくつか?
(2)1辺の長さが7cmの正三角形と、角度が45度、30度、底辺が7cmの三角形の面積の差はいくつか?(動画の図を参照)
(3)1辺9cmの正方形の内部にある、正三角形2つと正方形1つの面積の和はいくつか?(動画の図を参照)
この動画を見る
渋谷教育学園渋谷中2022入試問題大問3
(1)頂角30度、等辺の長さが5cmの二等辺三角形の面積はいくつか?
(2)1辺の長さが7cmの正三角形と、角度が45度、30度、底辺が7cmの三角形の面積の差はいくつか?(動画の図を参照)
(3)1辺9cmの正方形の内部にある、正三角形2つと正方形1つの面積の和はいくつか?(動画の図を参照)
【中学受験算数】『駒東の2021年入試の良問を勢いで解説してみた』

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#文章題#文章題その他#駒場東邦中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
駒場東邦中2021年算数入試問題大問大問4
2021、6564のように連続した2桁の数を並べた4桁の整数を考える。
(1)このような整数は全部で何個あるか?
(2)このような整数全ての平均はいくつか?
(3)このような4桁の整数のうち、47の倍数を全て求めよ。
この動画を見る
駒場東邦中2021年算数入試問題大問大問4
2021、6564のように連続した2桁の数を並べた4桁の整数を考える。
(1)このような整数は全部で何個あるか?
(2)このような整数全ての平均はいくつか?
(3)このような4桁の整数のうち、47の倍数を全て求めよ。
【算数】小学生すごすぎ!灘中学の入試問題解いてみた【中学受験】 #Shorts

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#灘中学校
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
15÷4=3.75,15÷125=0.12のように15をある正の整数で割るとき、ちょうど小数第2位を求めたところで割り算が終わる。
このような正の整数は4と125を含めて$□$個である。
この動画を見る
15÷4=3.75,15÷125=0.12のように15をある正の整数で割るとき、ちょうど小数第2位を求めたところで割り算が終わる。
このような正の整数は4と125を含めて$□$個である。
【算数】灘中学の整数問題を解いてみた【中学受験】 #Shorts

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#灘中学校
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
異なる4つの整数を小さい方から順に並べ、隣り合った2数の和を求めると、それぞれ28,32,59であった。4つの整数の中で最も大きい数は$□$である。
この動画を見る
異なる4つの整数を小さい方から順に並べ、隣り合った2数の和を求めると、それぞれ28,32,59であった。4つの整数の中で最も大きい数は$□$である。
【算数】小学生すごすぎ!連続する5つの整数の積【中学受験】 #Shorts

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#灘中学校
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
連続した5つの整数の積が2441880であるとき、これら5つの整数のうち最も小さいものを求めよ。
この動画を見る
連続した5つの整数の積が2441880であるとき、これら5つの整数のうち最も小さいものを求めよ。
【算数】これを小学生が解く!?中高生解けますか?【中学受験】 #Shorts

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#灘中学校
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
5桁の36の倍数で、2,3,5のどれもがいずれかの桁に現れる整数のうち、最も小さいものを求めよ。
この動画を見る
5桁の36の倍数で、2,3,5のどれもがいずれかの桁に現れる整数のうち、最も小さいものを求めよ。
【受験算数】数の性質:海城過去問~積と最大公約数から整数を求める!【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#過去問解説(学校別)#海城中学
教材:
#予習シリーズ#予習シリーズ算数・小5上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2けたの整数が2つあります。この2つの整数の積は4080,最大公約数は4です。この2つの整数を求めなさい。
この動画を見る
2けたの整数が2つあります。この2つの整数の積は4080,最大公約数は4です。この2つの整数を求めなさい。
【受験算数】海城過去問~正六角形と正三角形の面積を比べる

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#海城中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
周の長さが6㎝の正六角形の面積は、周の長さが6㎝の正三角形の面積の何倍ですか。
この動画を見る
周の長さが6㎝の正六角形の面積は、周の長さが6㎝の正三角形の面積の何倍ですか。
【受験算数】豊島岡過去問~正方形をはみ出る円の面積の求め方

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#豊島岡女子学園中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
2010年豊島岡大問2(4)の図形問題です。
右の図のように、1辺の長さが3㎝の正方形の辺をそれぞれ3等分した点をすべて通る円があります。この円の面積は何㎠ですか。
この動画を見る
2010年豊島岡大問2(4)の図形問題です。
右の図のように、1辺の長さが3㎝の正方形の辺をそれぞれ3等分した点をすべて通る円があります。この円の面積は何㎠ですか。
【受験算数】筑駒の2022年入試の難問をガチ解説してみた

単元:
#過去問解説(学校別)#筑波大学附属駒場中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
[4]整理番号1~545の545人のお客さんが1列に並んでいて、3か所の窓口で受付をする。
1人に対してあきら君の窓口は10秒、さとし君の窓口は13秒、たかし君の窓口は15秒かかる。
お客さんは、整理番号の小さい順に、3か所の窓口のうち空いている窓口で受付を行う。
どの窓口も、受付しているお客さんが終わったら、すぐに次のお客さんの受付が始まる。
1か所の窓口に同時に2人以上のお客さんが行くことはない。
開場と同時に、整理番号①のお客さんがあきら君の窓口に、②のお客さんがさとし君の窓口に、③のお客さんがたかし君の窓口に行くとして次の問いに答えなさい。
(1)あきら君が受付をするちょうど30人目のお客さんの整理番号を答えなさい。
(2)(ア)整理番号165のお客さんの受付が終わるのは開場から何秒後ですか?
(イ)整理番号165のお客さんの受付をするのは、あきら君・さとし君・たかし君の誰ですか?
開場からしばらくして、窓口のあきら君・さとし君・たかし君のうちの一人が、あるお客さんの受付を終えると同時にゆたか君と交代しました。ゆたか君がお客さん1人に対してかかる時間は8秒です。この結果、開場からちょうど2022秒後に、整理番号545のお客さんの受付が終わりました。
(3)ゆたか君は、開場から何秒後にあきら君・さとし君・ゆたか君のうちの誰と交代しましたか?
この動画を見る
[4]整理番号1~545の545人のお客さんが1列に並んでいて、3か所の窓口で受付をする。
1人に対してあきら君の窓口は10秒、さとし君の窓口は13秒、たかし君の窓口は15秒かかる。
お客さんは、整理番号の小さい順に、3か所の窓口のうち空いている窓口で受付を行う。
どの窓口も、受付しているお客さんが終わったら、すぐに次のお客さんの受付が始まる。
1か所の窓口に同時に2人以上のお客さんが行くことはない。
開場と同時に、整理番号①のお客さんがあきら君の窓口に、②のお客さんがさとし君の窓口に、③のお客さんがたかし君の窓口に行くとして次の問いに答えなさい。
(1)あきら君が受付をするちょうど30人目のお客さんの整理番号を答えなさい。
(2)(ア)整理番号165のお客さんの受付が終わるのは開場から何秒後ですか?
(イ)整理番号165のお客さんの受付をするのは、あきら君・さとし君・たかし君の誰ですか?
開場からしばらくして、窓口のあきら君・さとし君・たかし君のうちの一人が、あるお客さんの受付を終えると同時にゆたか君と交代しました。ゆたか君がお客さん1人に対してかかる時間は8秒です。この結果、開場からちょうど2022秒後に、整理番号545のお客さんの受付が終わりました。
(3)ゆたか君は、開場から何秒後にあきら君・さとし君・ゆたか君のうちの誰と交代しましたか?
【受験算数】早稲田中過去問解説:図形の問題と思いきや場合の数!

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#早稲田中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
2007年早稲田中学大問2(2)の問題です。
下の図2のように、高さが6㎝の正三角形の内部の点Pから辺BC、CA、ABへ垂線を引き、その長さをそれぞれxcm、ycm、zcmとします。
x、y、zがすべて整数であるような点Pは全部で何個ありますか。
この動画を見る
2007年早稲田中学大問2(2)の問題です。
下の図2のように、高さが6㎝の正三角形の内部の点Pから辺BC、CA、ABへ垂線を引き、その長さをそれぞれxcm、ycm、zcmとします。
x、y、zがすべて整数であるような点Pは全部で何個ありますか。
【受験算数】早稲田中過去問解説:円の中の三角形の面積を求める

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#早稲田中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
2007年早稲田中学②大問2(2)です。
図2の点A、B、C、D、E、F、G、Hは半径5㎝の円の周を8等分する点です。三角形ABDの面積は何㎠ですか。
この動画を見る
2007年早稲田中学②大問2(2)です。
図2の点A、B、C、D、E、F、G、Hは半径5㎝の円の周を8等分する点です。三角形ABDの面積は何㎠ですか。
【第46問】栄東中学2020年の入試問題【気付けばスッキリ!受験算数】

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#栄東中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
2020桁の777…777を37で割ったあまりを求めよ
※3×37=111を利用せよ
この動画を見る
2020桁の777…777を37で割ったあまりを求めよ
※3×37=111を利用せよ
【第45問】かえつ有明中学2010年の入試問題【気付けばスッキリ!受験算数】

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#かえつ有明中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
137,194,289をある整数で割ると余りがすべて等しくなる。
この整数を求めよ。
この動画を見る
137,194,289をある整数で割ると余りがすべて等しくなる。
この整数を求めよ。
【第44問】駒場東邦中学2014年の入試問題【気付けばスッキリ!受験算数】
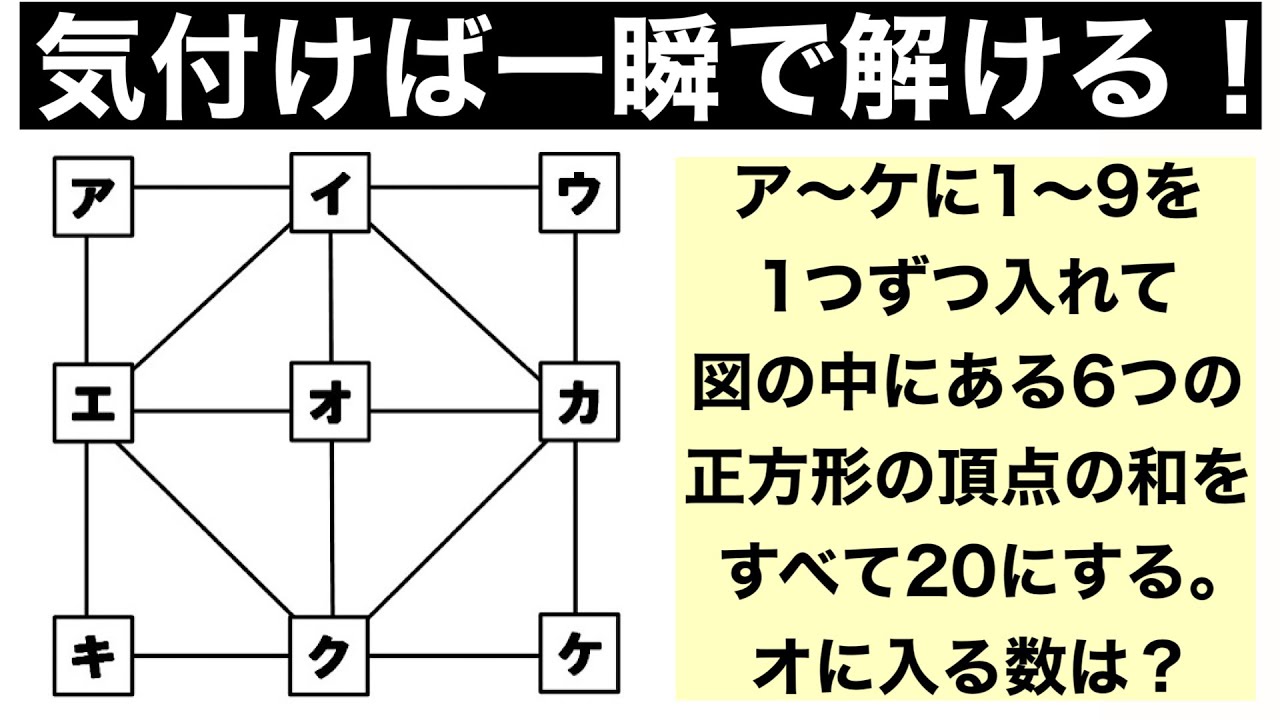
単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#駒場東邦中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
ア~ケに1~9を1つずつ入れて図の中にある6つの正方形の頂点の和をすべて20にするとき、オに入る数は?
この動画を見る
ア~ケに1~9を1つずつ入れて図の中にある6つの正方形の頂点の和をすべて20にするとき、オに入る数は?
【第43問】栄東中学2020年の入試問題【気付けばスッキリ!受験算数】
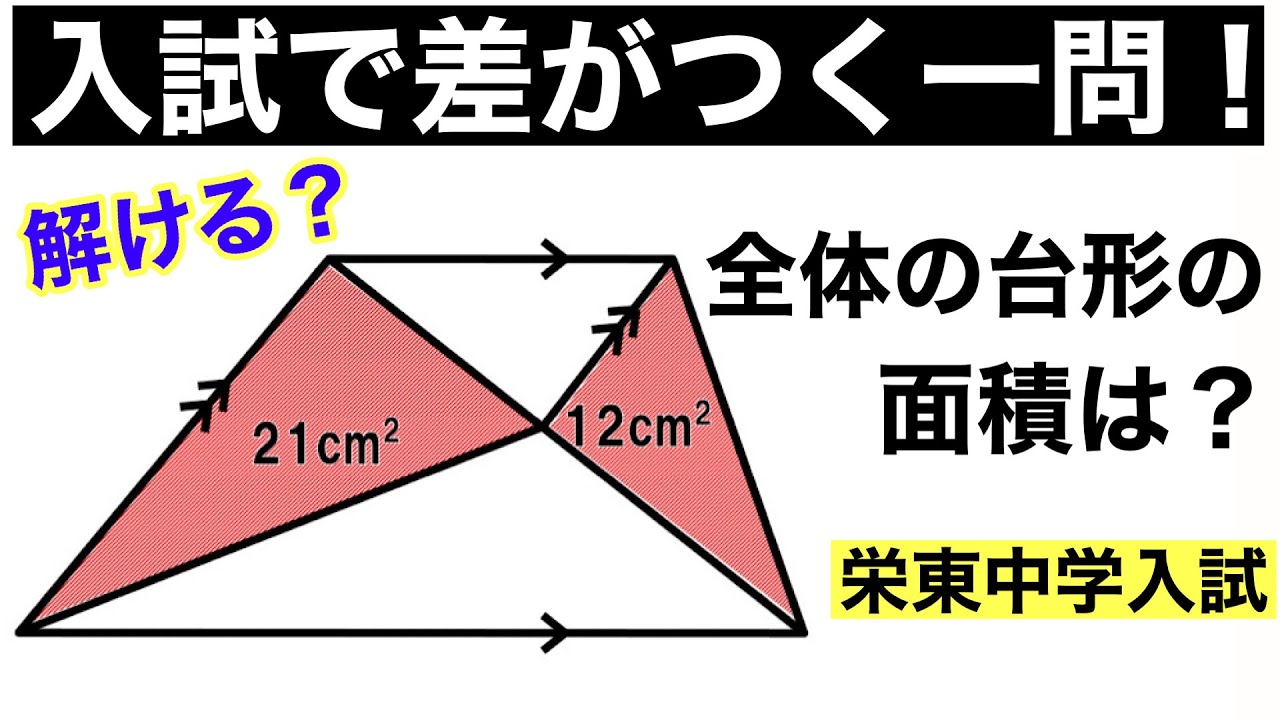
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#栄東中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
全体の台形の面積は?
この動画を見る
全体の台形の面積は?
【第42問】山手学院中学2019年の入試問題【気付けばスッキリ!受験算数】
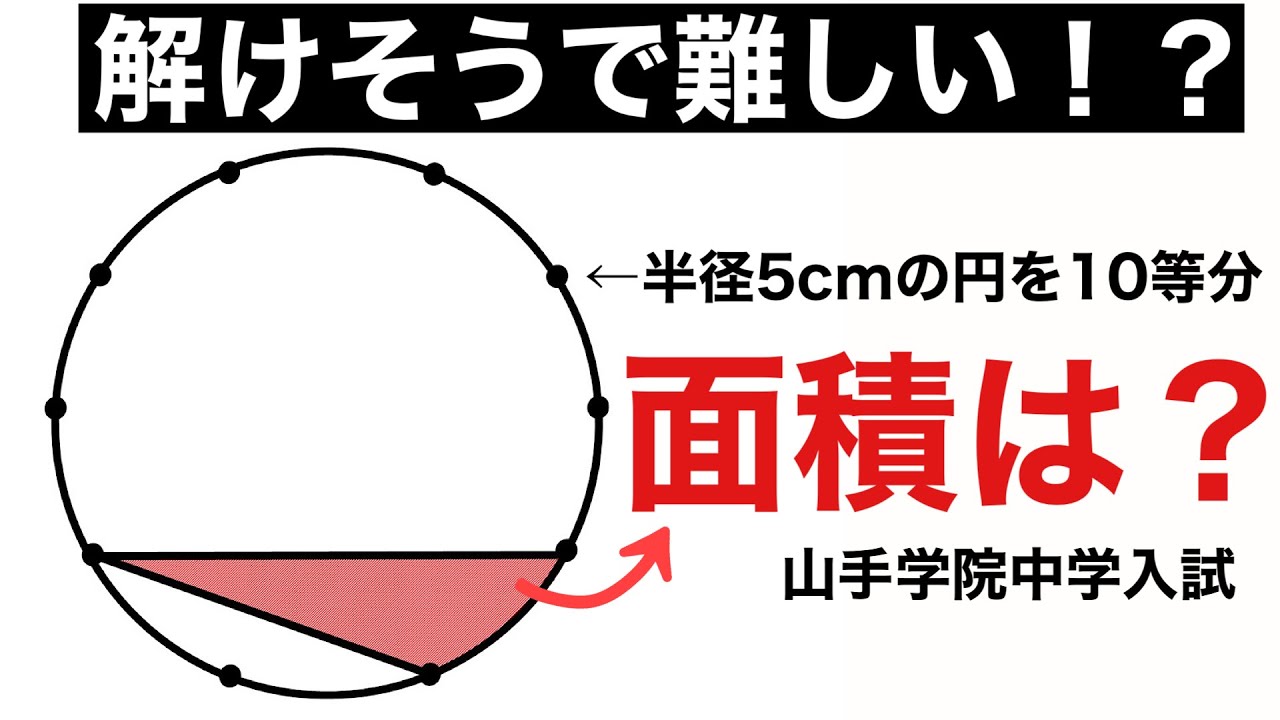
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#山手学院中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
半径5cmの円を10等分した点
色の部分の面積は?
この動画を見る
半径5cmの円を10等分した点
色の部分の面積は?
【第41問】東大寺学園中学2017年の入試問題【気付けばスッキリ!受験算数】
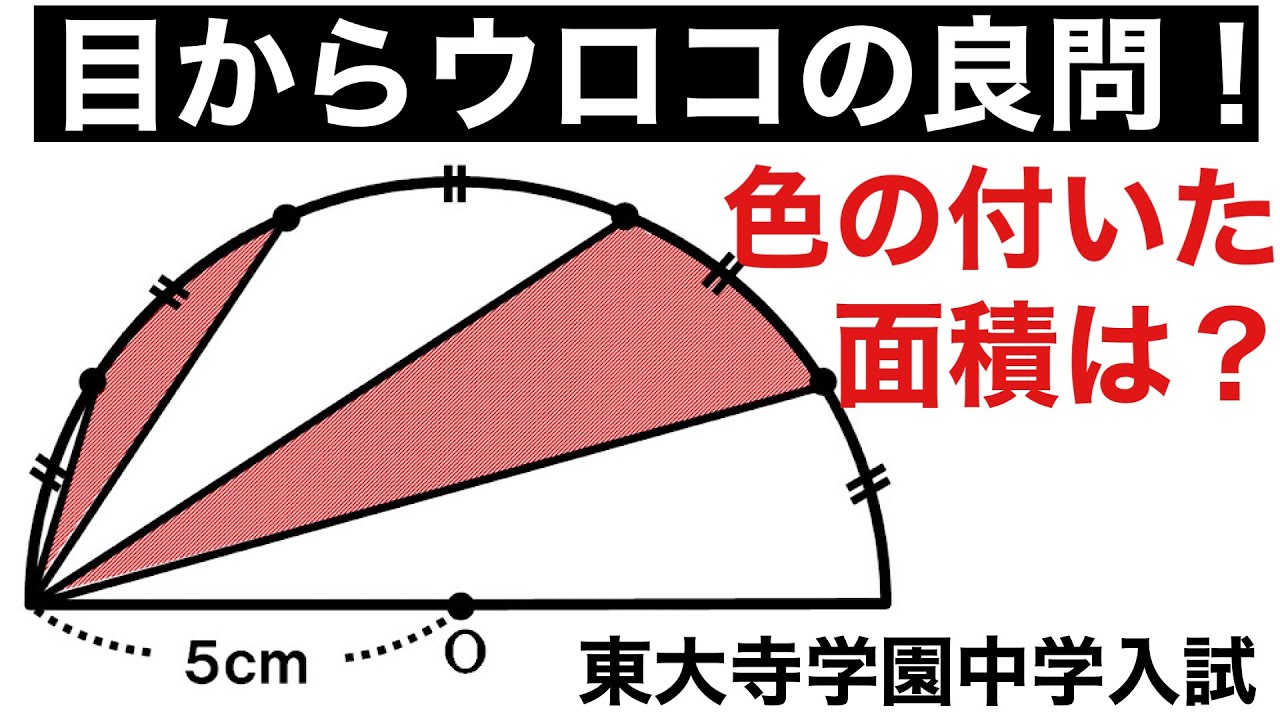
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#東大寺学園中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
色のついた部分の面積は?
この動画を見る
色のついた部分の面積は?
【第40問】西大和学園中学2020年の入試問題【気付けばスッキリ!受験算数】

【第39問】四天王寺中学2020年の入試問題【気付けばスッキリ!受験算数】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#四天王寺中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
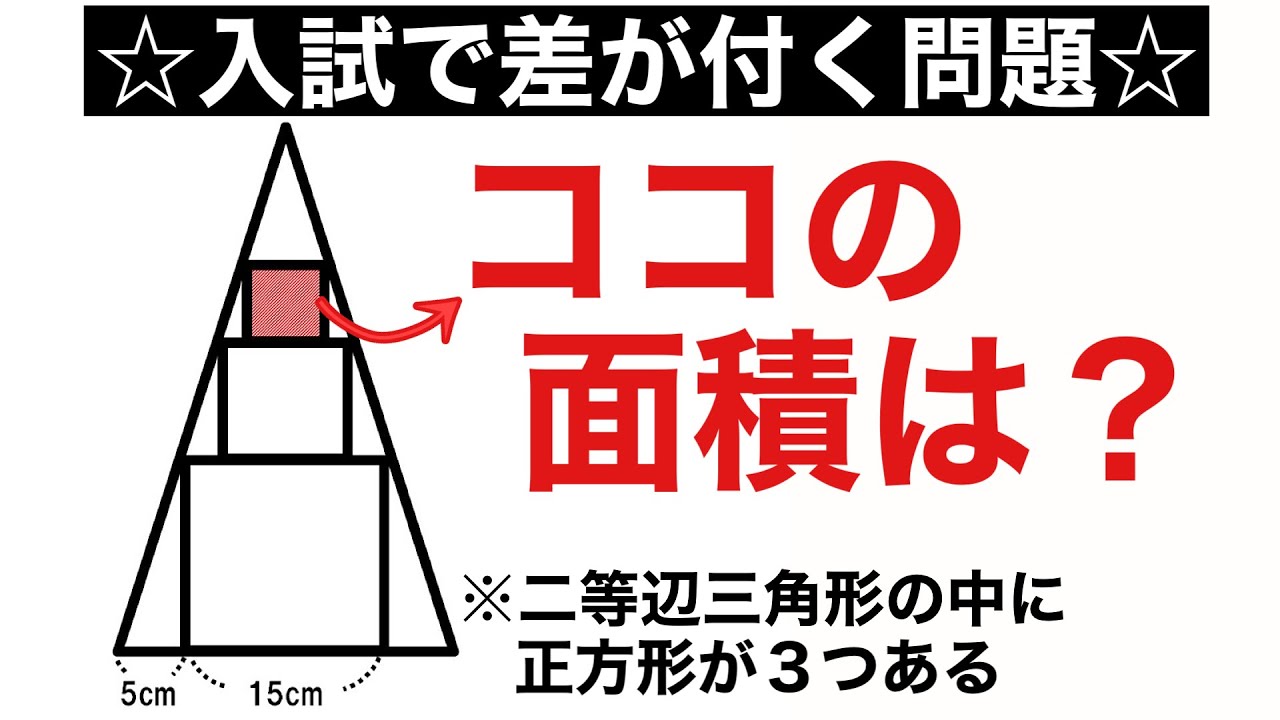
問題文全文(内容文):
ココの面積は?
この動画を見る
ココの面積は?
【第38問】洗足学園中学2020年の入試問題【気付けばスッキリ!受験算数】
単元:
#過去問解説(学校別)#洗足学園中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
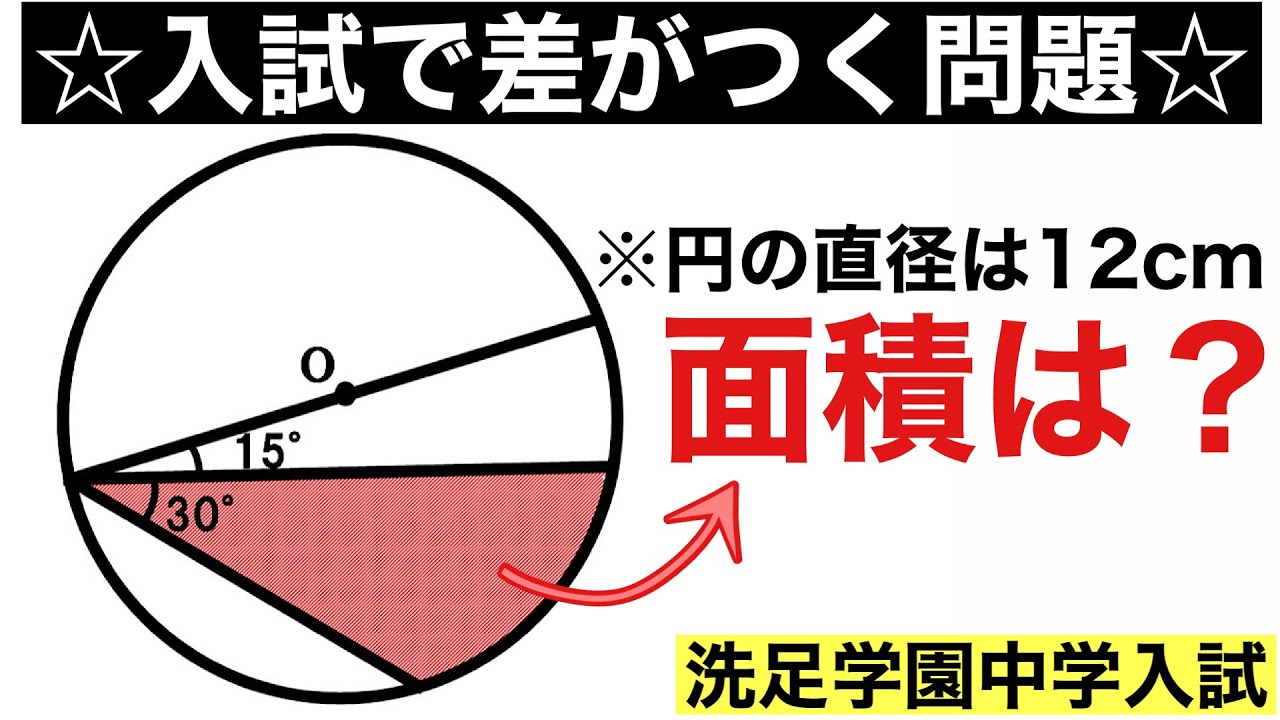
洗足学園中学2020年の入試問題解説
円の問題はまずこれをしましょう!
この動画を見る
洗足学園中学2020年の入試問題解説
円の問題はまずこれをしましょう!
【第34問】学習院女子中等科2020年の入試問題【気付けばスッキリ!受験算数】

単元:
#過去問解説(学校別)#学習院女子中等科
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
直線100本を書いたとき最も多い交点は何個??
きまりを見つけましょう!
この動画を見る
直線100本を書いたとき最も多い交点は何個??
きまりを見つけましょう!
