問題文全文(内容文):
①右の図1のような$\triangle ABC$があります。
点$D、E$はそれぞれ辺$AB、BC$上の点で、$\angle BDE =\angle ACB$です。
$AD = 2cm 、 DB = 8cm 、 BE = 6cm$のとき、$EC$の長さを求めなさい。
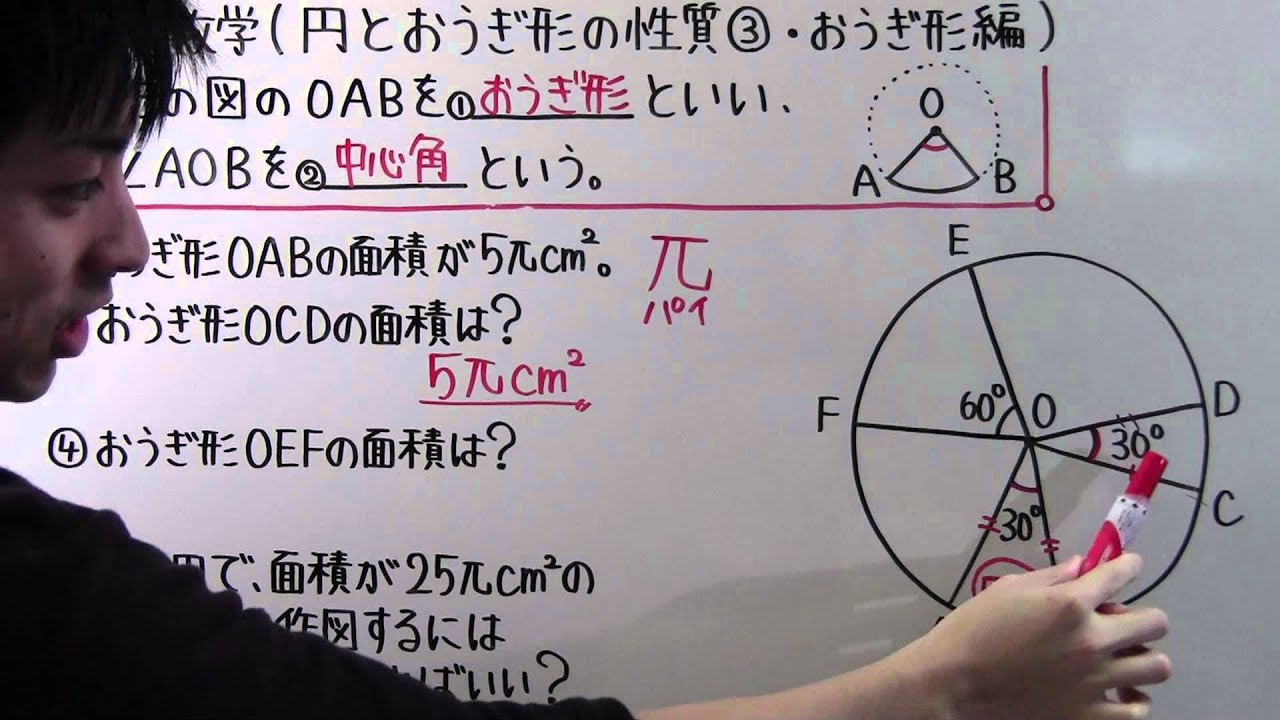
② 右の図2は、正方形$ABCD$と、おうぎ形$BAC$、おうぎ形$CBD$を組み合わせたものです。
点$E$は$\stackrel{\huge\frown}{AC}$と$\stackrel{\huge\frown}{BD}$との交点です。
正方形$ABCD$の1辺の長さが$12cm$のとき、$\stackrel{\huge\frown}{BE}$の長さを求めなさい。 ただし、円周率は$\pi$とします。
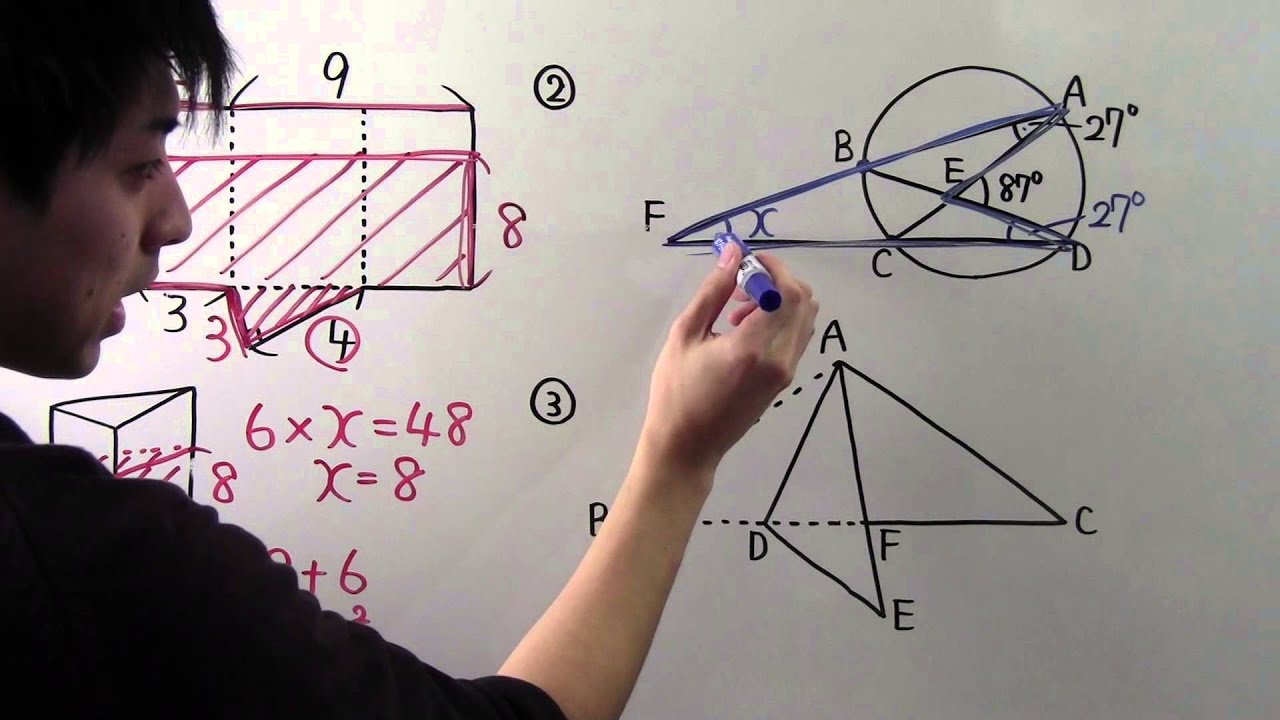
③右の図3のような四角形$ABCD$があり、対角線$AC$と対角線$BD$との交点を$E$とする。
線分$BE$上に、2点$B、E$と異なる点$F$をとり、直線$AF$と辺$BC$との交点を$G$とする。
四角形$ABCD$の面積が$50cm²$、$△AGC$の面積が$30cm$、
$BF:FD=3:4、AF:FG=2:1$であるとき、$△ACD$の面積は何$cm^2$か。
図は動画内参照
①右の図1のような$\triangle ABC$があります。
点$D、E$はそれぞれ辺$AB、BC$上の点で、$\angle BDE =\angle ACB$です。
$AD = 2cm 、 DB = 8cm 、 BE = 6cm$のとき、$EC$の長さを求めなさい。
② 右の図2は、正方形$ABCD$と、おうぎ形$BAC$、おうぎ形$CBD$を組み合わせたものです。
点$E$は$\stackrel{\huge\frown}{AC}$と$\stackrel{\huge\frown}{BD}$との交点です。
正方形$ABCD$の1辺の長さが$12cm$のとき、$\stackrel{\huge\frown}{BE}$の長さを求めなさい。 ただし、円周率は$\pi$とします。
③右の図3のような四角形$ABCD$があり、対角線$AC$と対角線$BD$との交点を$E$とする。
線分$BE$上に、2点$B、E$と異なる点$F$をとり、直線$AF$と辺$BC$との交点を$G$とする。
四角形$ABCD$の面積が$50cm²$、$△AGC$の面積が$30cm$、
$BF:FD=3:4、AF:FG=2:1$であるとき、$△ACD$の面積は何$cm^2$か。
図は動画内参照
単元:
#数学(中学生)#中1数学#中2数学#中3数学#円#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図1のような$\triangle ABC$があります。
点$D、E$はそれぞれ辺$AB、BC$上の点で、$\angle BDE =\angle ACB$です。
$AD = 2cm 、 DB = 8cm 、 BE = 6cm$のとき、$EC$の長さを求めなさい。
② 右の図2は、正方形$ABCD$と、おうぎ形$BAC$、おうぎ形$CBD$を組み合わせたものです。
点$E$は$\stackrel{\huge\frown}{AC}$と$\stackrel{\huge\frown}{BD}$との交点です。
正方形$ABCD$の1辺の長さが$12cm$のとき、$\stackrel{\huge\frown}{BE}$の長さを求めなさい。 ただし、円周率は$\pi$とします。
③右の図3のような四角形$ABCD$があり、対角線$AC$と対角線$BD$との交点を$E$とする。
線分$BE$上に、2点$B、E$と異なる点$F$をとり、直線$AF$と辺$BC$との交点を$G$とする。
四角形$ABCD$の面積が$50cm²$、$△AGC$の面積が$30cm$、
$BF:FD=3:4、AF:FG=2:1$であるとき、$△ACD$の面積は何$cm^2$か。
図は動画内参照
①右の図1のような$\triangle ABC$があります。
点$D、E$はそれぞれ辺$AB、BC$上の点で、$\angle BDE =\angle ACB$です。
$AD = 2cm 、 DB = 8cm 、 BE = 6cm$のとき、$EC$の長さを求めなさい。
② 右の図2は、正方形$ABCD$と、おうぎ形$BAC$、おうぎ形$CBD$を組み合わせたものです。
点$E$は$\stackrel{\huge\frown}{AC}$と$\stackrel{\huge\frown}{BD}$との交点です。
正方形$ABCD$の1辺の長さが$12cm$のとき、$\stackrel{\huge\frown}{BE}$の長さを求めなさい。 ただし、円周率は$\pi$とします。
③右の図3のような四角形$ABCD$があり、対角線$AC$と対角線$BD$との交点を$E$とする。
線分$BE$上に、2点$B、E$と異なる点$F$をとり、直線$AF$と辺$BC$との交点を$G$とする。
四角形$ABCD$の面積が$50cm²$、$△AGC$の面積が$30cm$、
$BF:FD=3:4、AF:FG=2:1$であるとき、$△ACD$の面積は何$cm^2$か。
図は動画内参照
投稿日:2017.12.26