問題文全文(内容文)：
①$13 + 3\times (- 6)$を計算せよ。

②$3(2a + 3) - 2(5a + 4)$ を計算せよ。

③$a = - 3 , b = 4$とき、$3a^2-5b$の値を求めよ。

④$\dfrac{30}{\sqrt5}+\sqrt{20}$を計算せよ。

⑤ 1次方程式$3x-8=7x+16$を解け。

⑥2次方程式$(x + 1) ^ 2 = x + 13$を解け。

⑦関数$y =\dfrac{2}{3}x^2$について、
$x$の変域が$-1\leqq x \leqq 3$のときの$y$の変域を求めよ。

⑧$\boxed{1},\boxed{3},\boxed{5},\boxed{7},\boxed{9}$のカードが1枚ずつある。
この5枚のカードから、同時に2枚のカードを取り出すとき、
その2枚のカードにかかれている数の和が10以上になる確率を求めよ。
ただし、どのカードを取り出すことも同様に確からしいものとする。

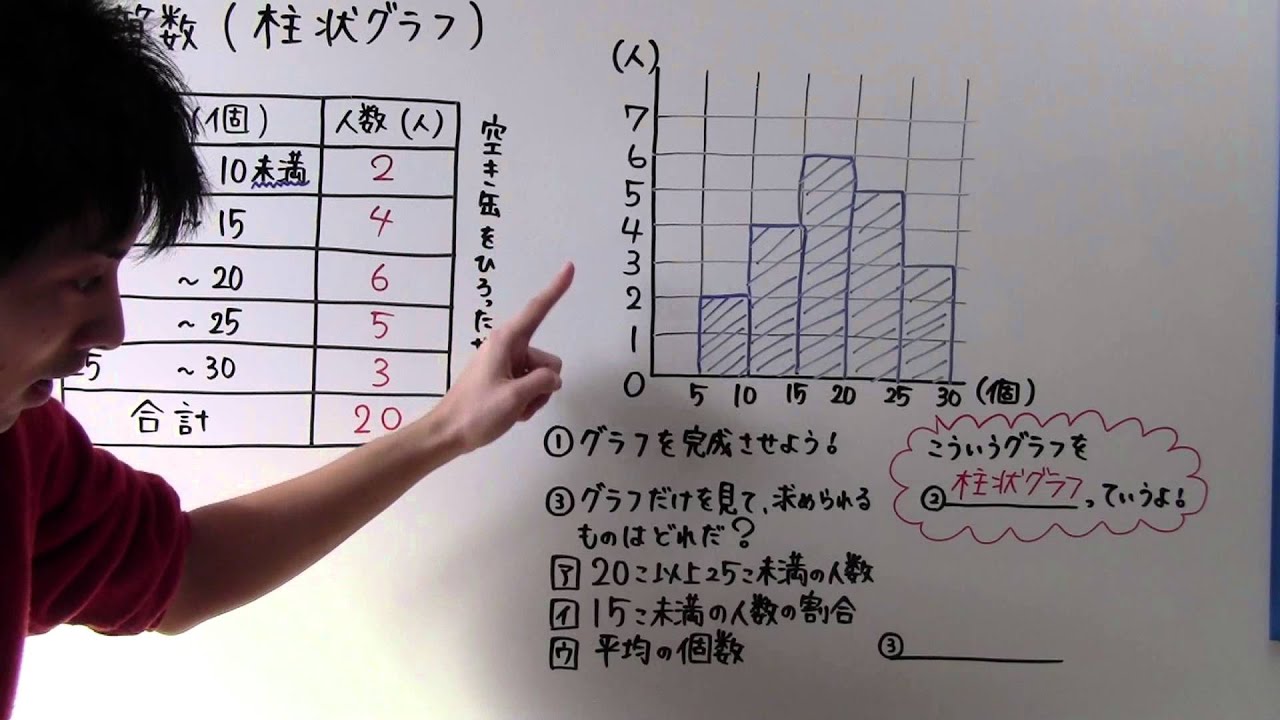
⑨右の表は、A中学校とB中学校の生徒を対象に、
携帯電話やスマートフォンの1日あたりの使用時間を調査し、
その結果を度数分布表に整理したものである。
この表をもとに、A中学校とB中学校の「0時間以上1時間未満」の階級の相対度数のうち、
大きい方の相対度数を四捨五入して小数第2位まで求めよ。

図は動画内参照