問題文全文(内容文):
中1~第46回 対称移動~
例題
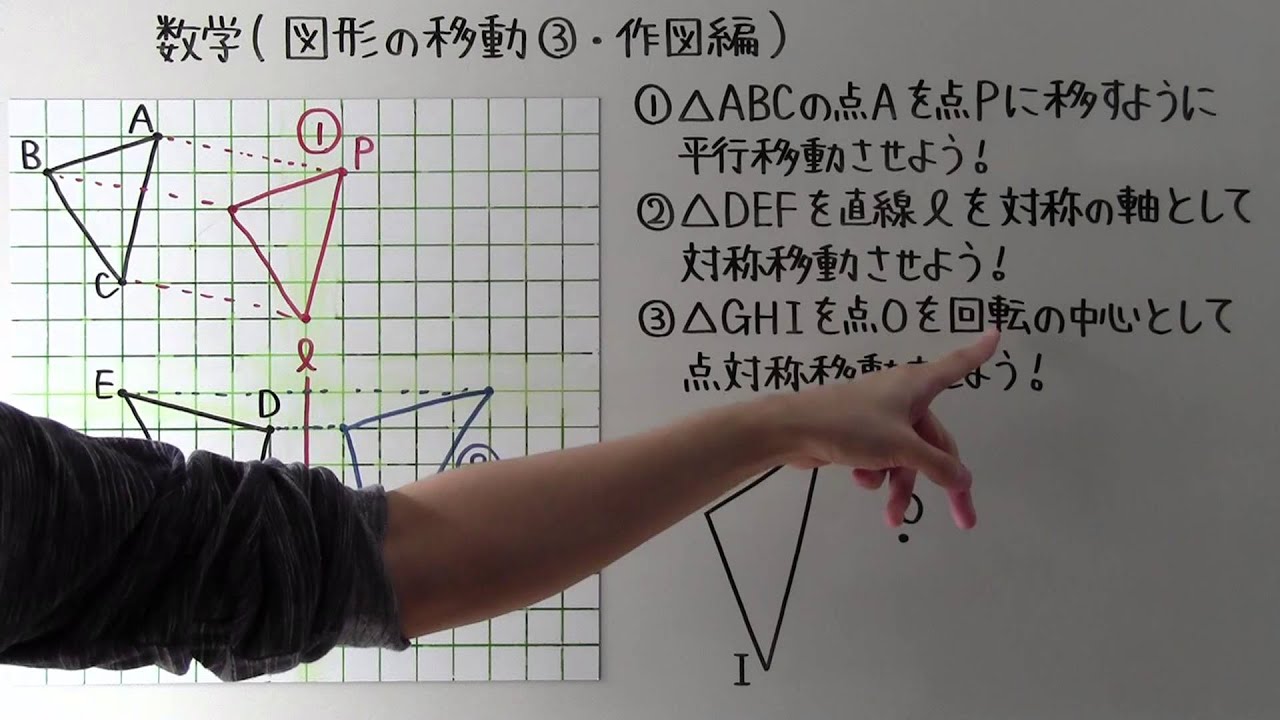
次の図の△DEFは△ABCを直線しを対称の軸として対称移動させたものだ。
(1) 直線ℓと垂直な線分を すべて答えなさい。
(2)線分ABと等しい線分を 答えなさい。
(3)線分BRと等しい線分を 答えなさい。
中1~第46回 対称移動~
例題
次の図の△DEFは△ABCを直線しを対称の軸として対称移動させたものだ。
(1) 直線ℓと垂直な線分を すべて答えなさい。
(2)線分ABと等しい線分を 答えなさい。
(3)線分BRと等しい線分を 答えなさい。
単元:
#数学(中学生)#中1数学#平面図形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第46回 対称移動~
例題
次の図の△DEFは△ABCを直線しを対称の軸として対称移動させたものだ。
(1) 直線ℓと垂直な線分を すべて答えなさい。
(2)線分ABと等しい線分を 答えなさい。
(3)線分BRと等しい線分を 答えなさい。
中1~第46回 対称移動~
例題
次の図の△DEFは△ABCを直線しを対称の軸として対称移動させたものだ。
(1) 直線ℓと垂直な線分を すべて答えなさい。
(2)線分ABと等しい線分を 答えなさい。
(3)線分BRと等しい線分を 答えなさい。
投稿日:2020.11.22