【視聴者様リクエスト動画】円錐の中心角と側面積を一瞬で求める超便利公式！どうして成り立つかも説明します！ - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 立体図形 > 体積・表面積・回転体・水量・変化のグラフ > 【視聴者様リクエスト動画】円錐の中心角と側面積を一瞬で求める超便利公式！どうして成り立つかも説明します！

【視聴者様リクエスト動画】円錐の中心角と側面積を一瞬で求める超便利公式！どうして成り立つかも説明します！

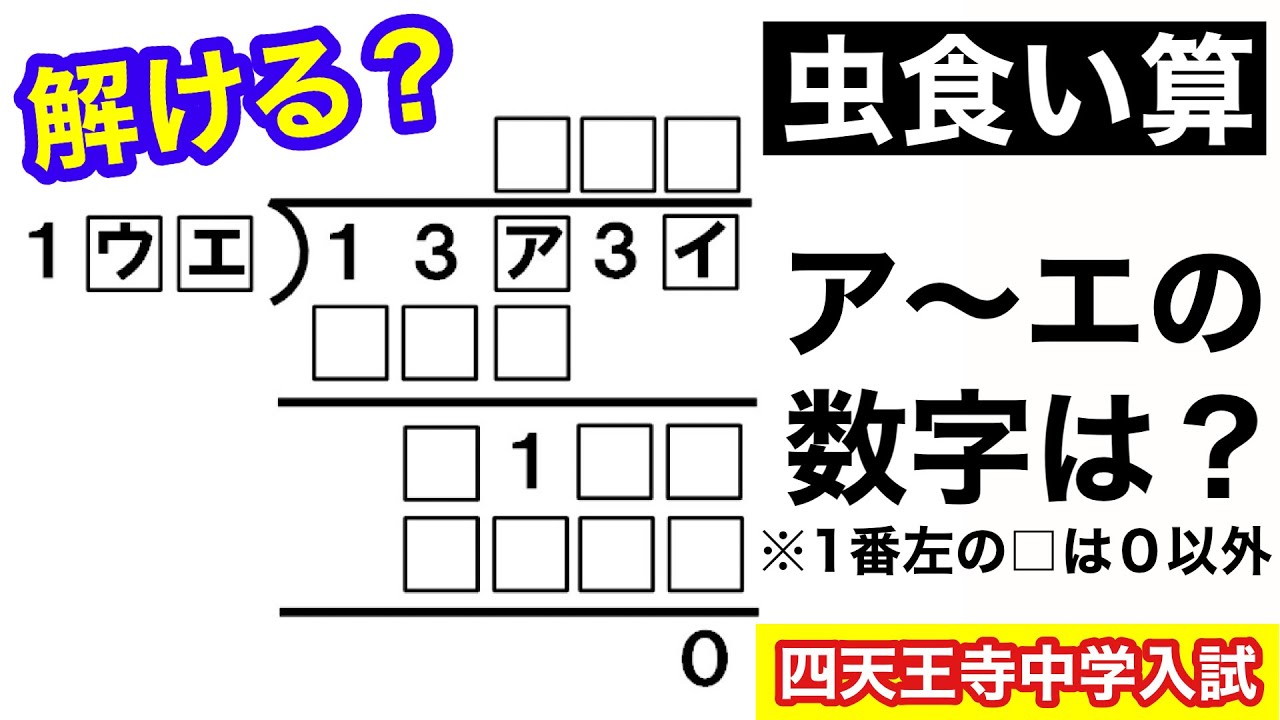
問題文全文(内容文)：
円錐の中心角と側面積を求める公式解説
チャプター：

0:00　導入
1:22　円すいの中心角を求める超便利公式　成り立ち説明
4:26　円すいの中心角を求める超便利公式　提示
5:23　円すいの側面積を求める超便利公式　成り立ち説明
6:53　円すいの側面積を求める超便利公式　提示
8:32　エンディング

単元： #算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師： こばちゃん塾
問題文全文(内容文)：
円錐の中心角と側面積を求める公式解説
投稿日：2020.03.10

＜関連動画＞

n角形の内角と外角の和の簡単な求め方！【図形問題基礎講座44】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： こばちゃん塾
問題文全文(内容文)：
例1　下の五角形で㋐は何度？

例2　印をつけた5つの角の和は何度？

単元卒業テスト
下図の印をつけた7つの角の和は何度？

＊図は動画内参照
この動画を見る　

【受験算数】第１問あるきまりにしたがって、数が並んでいます。□にあてはまる数を答えなさい。（１）１，５，９，１３，１７，□，２５，…（２）１，３，９，２７，８１，□，７２９，…

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材： #SPX#5年算数D-支援#中学受験教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
第１問
あるきまりにしたがって、数が並んでいます。□にあてはまる数を答えなさい。
（１）１，５，９，１３，１７，□，２５，…
（２）１，３，９，２７，８１，□，７２９，…
（３）１，３，６，１０，１５，□，２８，…
（４）１，４，９，１６，２５，□，４９，…

第２問
あるきまりにしたがって、数が並んでいます。□にあてはまる数を答えなさい。
（１）１，５，９，１３，１７，□，２５，…
（２）１，３，９，２７，８１，□，７２９，…
（３）１，３，６，１０，１５，□，２８，…
（４）１，４，９，１６，２５，□，４９，…
この動画を見る　

○○に気づけば超簡単！小学生の知識だけで解けますか？【中学受験算数】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： こばちゃん塾
問題文全文(内容文)：
下図の半円の面積は?(円周率は3.14)

図は動画内参照
この動画を見る　

【裏技】×99の計算テクニック

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#数学(中学生)#数学(高校生)
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
×99の計算テクニック
この動画を見る　

予習シリーズ算数6年上　第13回数と規則性(2)重要問題１，２

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材： #予習シ#予習シ・算数・小6上#中学受験教材
指導講師： 重吉
問題文全文(内容文)：
数と規則性(2)
1 60をわると6あまる整数をすべて答えなさい。
2 次の整数の組の最大公約数を求めなさい。
(1)(30,48)
(2)(112,196,252)
この動画を見る　
Back to top