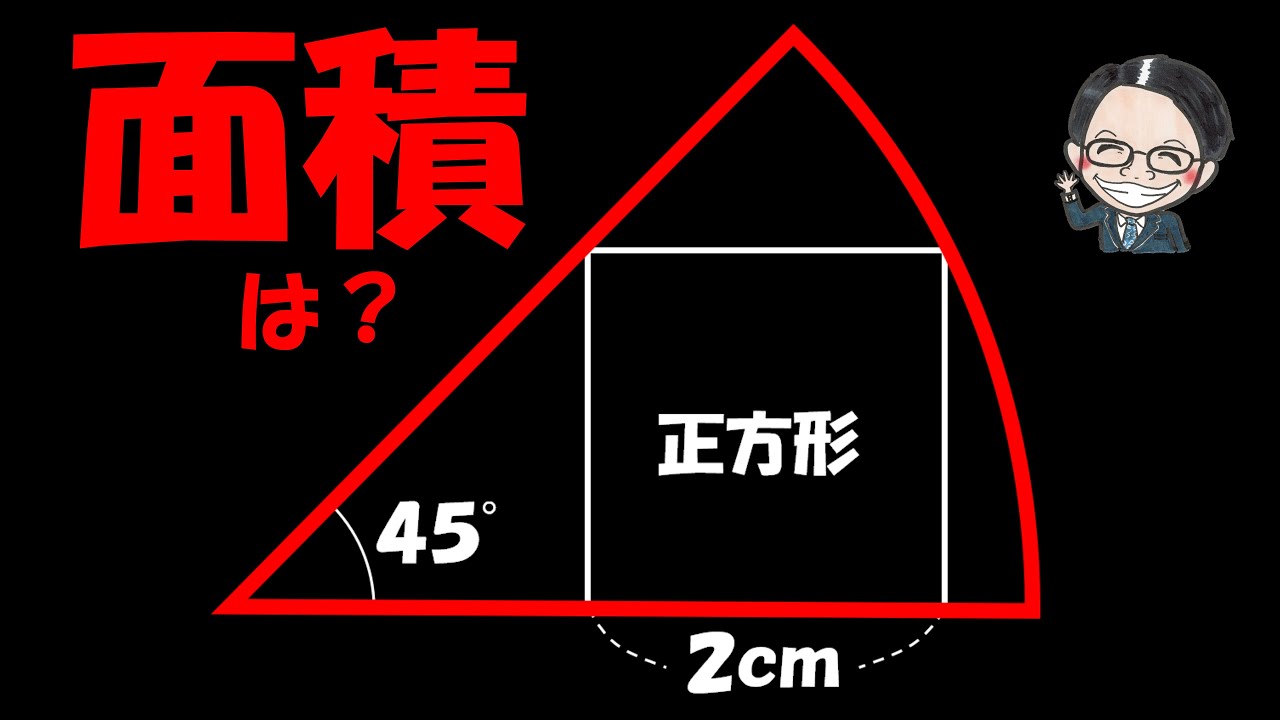
問題文全文(内容文):
①$e^{i \pi}+1=0$
②$\displaystyle \frac{a^2u}{at^2}=v^2 \frac{a^2u}{ax^2}$
③底辺$\times$高さ$\div 2$
④$x=\frac{-b \pm \sqrt{ b^2-4ac }}{2a}$
⑤$E=mc^2$
⑥$2 \pi r$
⑦$\displaystyle \frac{av}{at}+(v・\triangledown)v=-\frac{1}{p}\triangledown p+v \triangledown ^2v+f(x,t)$
⑧$\frac{4\pi r^3}{3}$
①$e^{i \pi}+1=0$
②$\displaystyle \frac{a^2u}{at^2}=v^2 \frac{a^2u}{ax^2}$
③底辺$\times$高さ$\div 2$
④$x=\frac{-b \pm \sqrt{ b^2-4ac }}{2a}$
⑤$E=mc^2$
⑥$2 \pi r$
⑦$\displaystyle \frac{av}{at}+(v・\triangledown)v=-\frac{1}{p}\triangledown p+v \triangledown ^2v+f(x,t)$
⑧$\frac{4\pi r^3}{3}$
単元:
#算数(中学受験)#その他#その他#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
①$e^{i \pi}+1=0$
②$\displaystyle \frac{a^2u}{at^2}=v^2 \frac{a^2u}{ax^2}$
③底辺$\times$高さ$\div 2$
④$x=\frac{-b \pm \sqrt{ b^2-4ac }}{2a}$
⑤$E=mc^2$
⑥$2 \pi r$
⑦$\displaystyle \frac{av}{at}+(v・\triangledown)v=-\frac{1}{p}\triangledown p+v \triangledown ^2v+f(x,t)$
⑧$\frac{4\pi r^3}{3}$
①$e^{i \pi}+1=0$
②$\displaystyle \frac{a^2u}{at^2}=v^2 \frac{a^2u}{ax^2}$
③底辺$\times$高さ$\div 2$
④$x=\frac{-b \pm \sqrt{ b^2-4ac }}{2a}$
⑤$E=mc^2$
⑥$2 \pi r$
⑦$\displaystyle \frac{av}{at}+(v・\triangledown)v=-\frac{1}{p}\triangledown p+v \triangledown ^2v+f(x,t)$
⑧$\frac{4\pi r^3}{3}$
投稿日:2024.04.30