2023高校入試数学解説78問目面積比愛知県 - 質問解決D.B.（データベース）

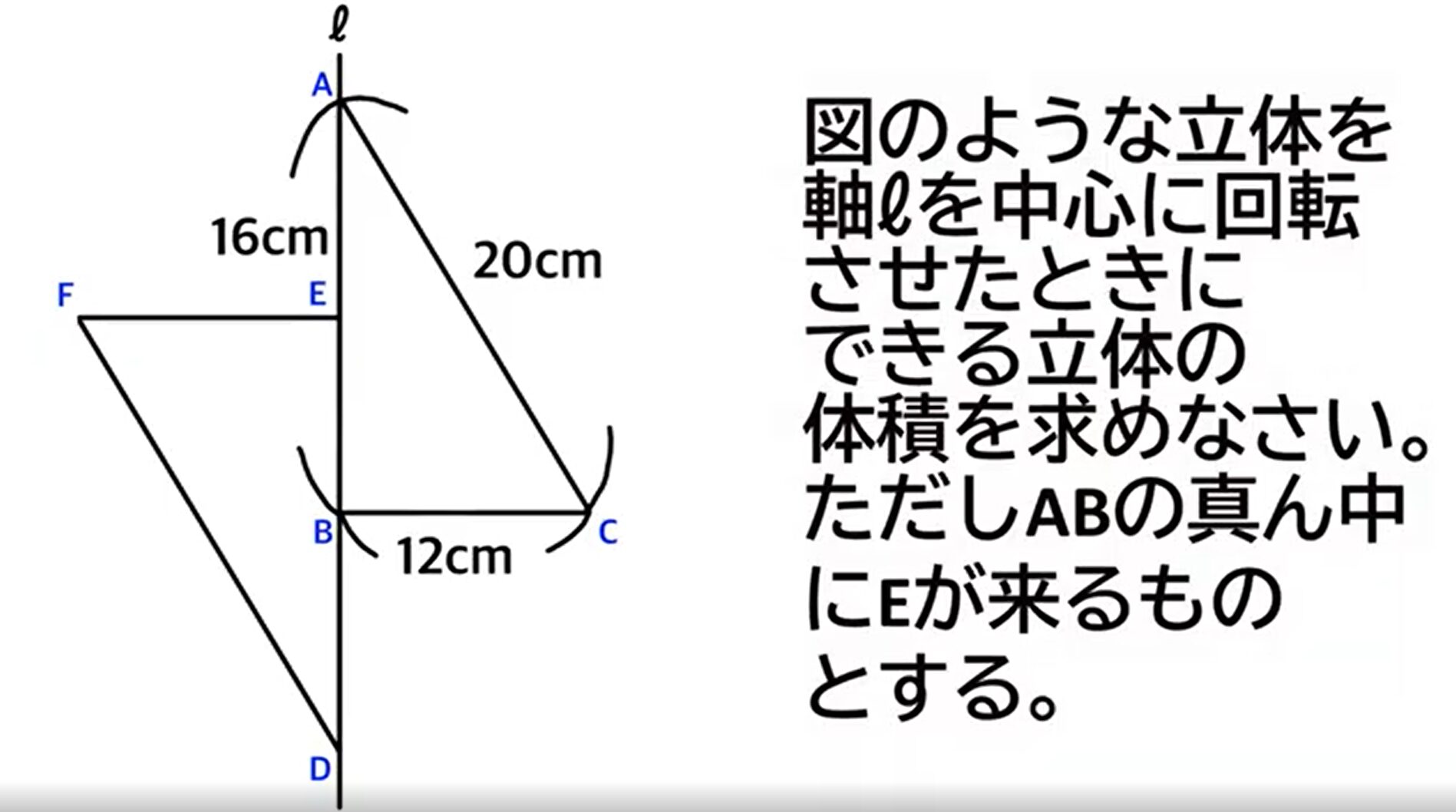
問題文全文(内容文)：
△DGHの面積は？
＊図は動画内参照

2023愛知県

単元： #数学(中学生)#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)

指導講師：数学を数楽に

問題文全文(内容文)：
△DGHの面積は？
＊図は動画内参照

2023愛知県

投稿日：2023.02.23

単元： #その他#立体図形#体積・表面積・回転体・水量・変化のグラフ#数学(高校生)#教員採用試験

指導講師：ますただ

問題文全文(内容文)：
$\boxed{4}$
領域$\sqrt x+\sqrt y \leqq 1$を
$y=x$を中心とする回転体の体積$V$を求めよ.
図は動画内参照

この動画を見る　

単元： #算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ

指導講師：中学受験算数・高校受験数学けいたくチャンネル

問題文全文(内容文)：
第54回水面の高さ④

例題
次の図のような容器に、深さ4cmまで水が入っています。

(1)この容器に入っている水の体積は何㎤ですか？

(2)この容器を、三角形ABCが底面になるように置いたとき、水面の高さは何cm になりますか。

この動画を見る　

単元： #算数(中学受験)#過去問解説(学校別)#立体図形#体積・表面積・回転体・水量・変化のグラフ#東京都市大学付属中学

指導講師：理数個別チャンネル

問題文全文(内容文)：
たて12cm、横6cmの長方形から、右図のように三角形を切り取ってできた図形を、直線lを軸にして1回転してできる図形の体積を求めよう。ただし円周率は3.14とします。

この動画を見る　

単元： #算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ

教材： #予習シ#予習シ・算数・小6上#中学受験教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
下の台形を、直線ℓを軸にして１回転させてできる立体について、次の問いに答えなさい。
⑴ 体積は何㎤ですか。
⑵ 表面積は何㎠ですか。

この動画を見る　

単元： #算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ

指導講師：こばちゃん塾

問題文全文(内容文)：
例1　下の円すいの側面の面積と中心角は？

例2　下の円すいは何回転で元の位置に戻る？

単元卒業テスト
下図はある立体の展開図でおうぎ形と半円です。□は何㎝？

＊図は動画内参照

この動画を見る　