問題文全文(内容文)：
センター試験まであと20日！
「ベストを出すためのメンタル調整術」についてお話しています。

問題文全文(内容文)：
${\large第4問}$
点$O$を原点とする座標空間に2点
$A(3,　3,　-6),$　$B(2+2\sqrt3,$　$2-2\sqrt3,　-4)$
をとる。3点$O,A,B$の定める平面を$\alpha$とする。また、$\alpha$に含まれる点$C$は

$\overrightarrow{ OA } \bot \overrightarrow{ OC },$　$\overrightarrow{ OB }・\overrightarrow{ OC }=24$　$\cdots$①

を満たすとする。

(1)　$|\overrightarrow{ OA }|=\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }},$　$|\overrightarrow{ OB }|=\boxed{\ \ ウ\ \ }\sqrt{\boxed{\ \ エ\ \ }}$であり、
$\overrightarrow{ OA }・\overrightarrow{ OB }=\boxed{\ \ オカ\ \ }$である。

(2)点$C$は平面$\alpha$上にあるので、実数$s,$　$t$を用いて、$\overrightarrow{ OC }=s\ \overrightarrow{ OA }+t\ \overrightarrow{ OB }$と
表すことができる。このとき、①から$s=\displaystyle \frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケ\ \ }},$　$t=\boxed{\ \ コ\ \ }$である。
したがって、$|\overrightarrow{ OC }|=\boxed{\ \ サ\ \ }\sqrt{\boxed{\ \ シ\ \ }}$である。

(3)$\overrightarrow{ CB }=\left(\boxed{\ \ ス\ \ },　\boxed{\ \ セ\ \ },　\boxed{\ \ ソタ\ \ }\right)$である。したがって、平面$\alpha$上の
四角形$OABC$は$\boxed{\ \ チ\ \ }$。
$\boxed{\ \ チ\ \ }$に当てはまるものを、次の⓪～④のうちから一つ選べ。
ただし、少なくとも一組の対辺が平行な四角形を台形という。

⓪正方形である
①正方形ではないが、長方形である
②長方形ではないが、平行四辺形である
③平行四辺形ではないが、台形である
④台形ではない

$\overrightarrow{ OA } \bot \overrightarrow{ OC }$であるので、四角形$OABC$の面積は$\boxed{\ \ ツテ\ \ }$である。

(4)$\overrightarrow{ OA } \bot \overrightarrow{ OD },$　$\overrightarrow{ OC }・\overrightarrow{ OD }=2\sqrt6$かつ$z$座標が1であるような点$D$の座標は
$(\boxed{\ \ ト\ \ }+\displaystyle \frac{\sqrt{\boxed{\ \ ナ\ \ }}}{\boxed{\ \ ニ\ \ }},$$　\boxed{\ \ ヌ\ \ }+\displaystyle \frac{\sqrt{\boxed{\ \ ネ\ \ }}}{\boxed{\ \ ノ\ \ }},　1)$
である。このとき$\angle COD=\boxed{\ \ ハヒ\ \ }°$である。
3点$O,C,D$の定める平面を$\beta$とする。$\alpha$と$\beta$は垂直であるので、三角形
$ABC$を底面とする四面体$DABC$の高さは$\sqrt{\boxed{\ \ フ\ \ }}$である。したがって、
四面体$DABC$の体積は$\boxed{\ \ ヘ\ \ }\sqrt{\boxed{\ \ ホ\ \ }}$　である。

2020センター試験過去問

問題文全文(内容文)：
${\large第5問}$
$\triangle ABC$において、辺$BC$を$7:1$に内分する点を$D$とし、辺$AC$を$7:1$に
内分する点を$E$とする。線分$AD$と線分$BE$の交点を$F$とし、直線$CF$
と辺$AB$の交点を$G$とすると

$\displaystyle \frac{GB}{AG}=\boxed{\ \ ア\ \ },　\displaystyle \frac{FD}{AF}=\displaystyle \frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }},$$　\displaystyle \frac{FC}{GF}=\displaystyle \frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$

である。したがって

$\displaystyle \frac{\triangle CDGの面積}{\triangle BFGの面積}=\displaystyle \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キク\ \ }}\displaystyle$

となる。

4点$B,D,F,G$が同一円周上にあり、かつ$FD=1$のとき

$AB=\boxed{\ \ ケコ\ \ }$

である。さらに、$AE=3\sqrt7$とするとき、$AE・AC=\boxed{\ \ サシ\ \ }$であり

$\angle AEG=\boxed{\ \ ス\ \ }$

である。$\boxed{\ \ ス\ \ }$に当てはまるものを、次の⓪～③のうちから一つ選べ。
⓪$\angle BGE$
①$\angle ADB$
②$\angle ABC$
③$\angle BAD$

2020センター試験過去問

問題文全文(内容文)：
${\large第5問}$
ある市の市立図書館の利用状況について調査を行った。

(1)ある高校の生徒720人全員を対象に、ある1週間に市立図書館で借りた本の
冊数について調査を行った。
その結果、1冊も借りなかった生徒が612人、1冊借りた生徒が54人、
2冊借りた生徒が36人であり、3冊借りた生徒が18人であった。
4冊以上借りた生徒はいなかった。

この高校の生徒から1人を無作為に選んだ時、その生徒が借りた本の冊数
を表す確率変数を$X$とする。

このとき、$X$の平均(期待値)は$E(X)=\displaystyle \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$であり、$X^2$の平均は
$E(X^2)=\displaystyle \frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。よって、$X$の標準偏差は
$\sigma(X)=\displaystyle \frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}\displaystyle$ である。

(2)市内の高校生全員を母集団とし、ある1週間に市立図書館を利用した生徒の
割合(母比率)を$p$とする。この母集団から600人を無作為に選んだ時、その
1週間に市立図書館を利用した生徒の数を確率変数$Y$で表す。

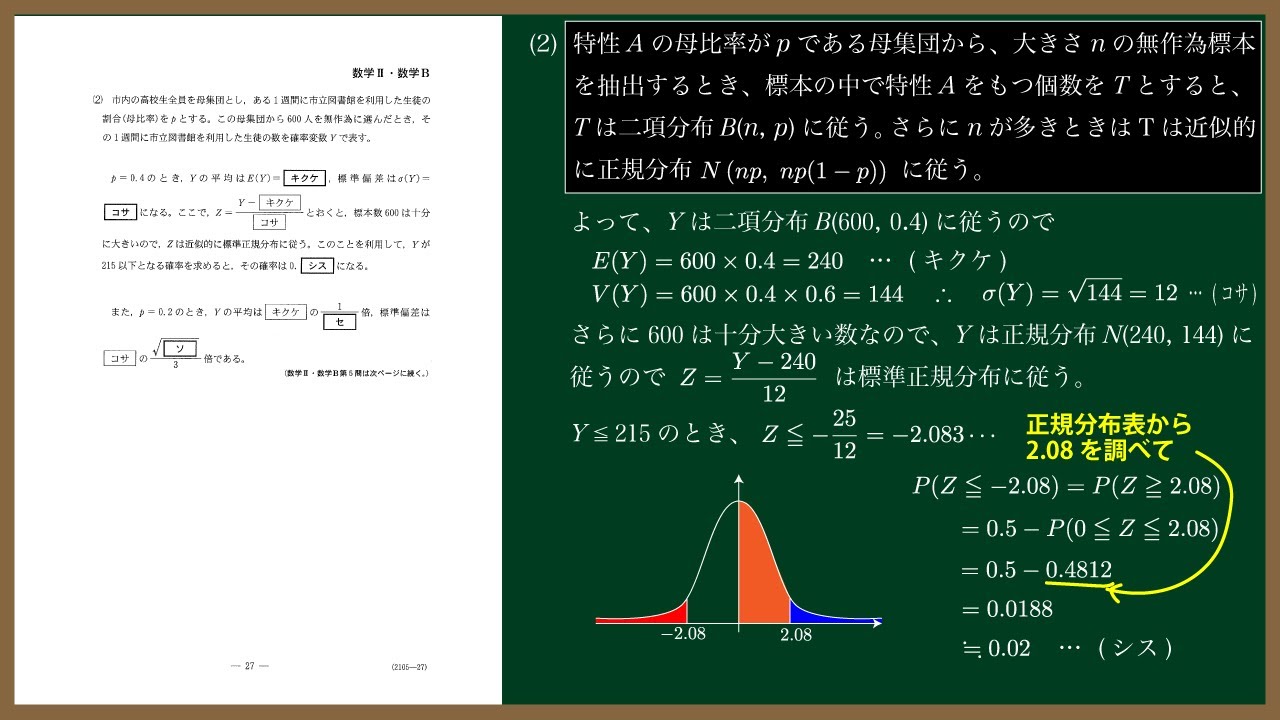
$p=0.4$のとき、$Y$の平均は$E(Y)=\boxed{\ \ キクケ\ \ }$、標準偏差は$\sigma(Y)=\boxed{\ \ コサ\ \ }$
になる。ここで、$Z=\displaystyle \frac{Y-\boxed{\ \ キクケ\ \ }}{\boxed{\ \ コサ\ \ }}\displaystyle$ とおくと、標本数600は
十分に大きいので、$Z$は近似的に標準正規分布に従う。このことを利用して、
$Y$が215以下となる確率を求めると、その確率は$0.\boxed{\ \ シス\ \ }$になる。

また、$p=0.2$のとき、$Y$の平均は$\boxed{\ \ キクケ\ \ }$の$\displaystyle \frac{1}{\boxed{\ \ セ\ \ }}$倍、
標準偏差は$\boxed{\ \ コサ\ \ }$の$\displaystyle \frac{\sqrt{\boxed{\ \ ソ\ \ }}}{3}$倍である。

(3)市立図書館に利用者登録のある高校生全員を母集団とする。1回あたりの
利用時間(分)を表す確率変数を$W$とし、$W$は母平均$m$,母標準偏差30の分布
に従うとする。この母集団から大きさ$n$の標本$W_1,W_2,\ldots,W_n$を無作為に
抽出した。
利用時間が60分をどの程度超えるかについて調査するために
$U_1=W_1-60,　U_2=W_2-60,　\ldots,　U_n=W_n-60$
とおくと、確率変数$U_1,U_2, \cdots, U_n$の平均と標準偏差はそれぞれ
$E(U_1)=E(U_2)=\cdots=E(U_n)$$=m-\boxed{\ \ タチ\ \ }$
$\sigma(U_1)=\sigma(U_2)=\cdots=\sigma(U_n)$$=\boxed{\ \ ツテ\ \ }$
である。

ここで、$t=m-60$として、$t$に対する信頼度95％の信頼区間を求めよう。
この母集団から無作為抽出された100人の生徒に対して$U_1,U_2, \cdots,U_m$の
値を調べたところ、その標本平均の値が50分であった。標本数は十分大きい
ことを利用して、この信頼区間を求めると
$\boxed{\ \ トナ\ \ }.\boxed{\ \ ニ\ \ } \leqq t \leqq \boxed{\ \ ヌネ\ \ }.\boxed{\ \ ノ\ \ }$
になる。

2020センター試験過去問

問題文全文(内容文)：
センター前日のあなたへ伝えたい言葉
「諦めるな！」ということについてお話しています。