地球ショートケーキは何キロカロリー？

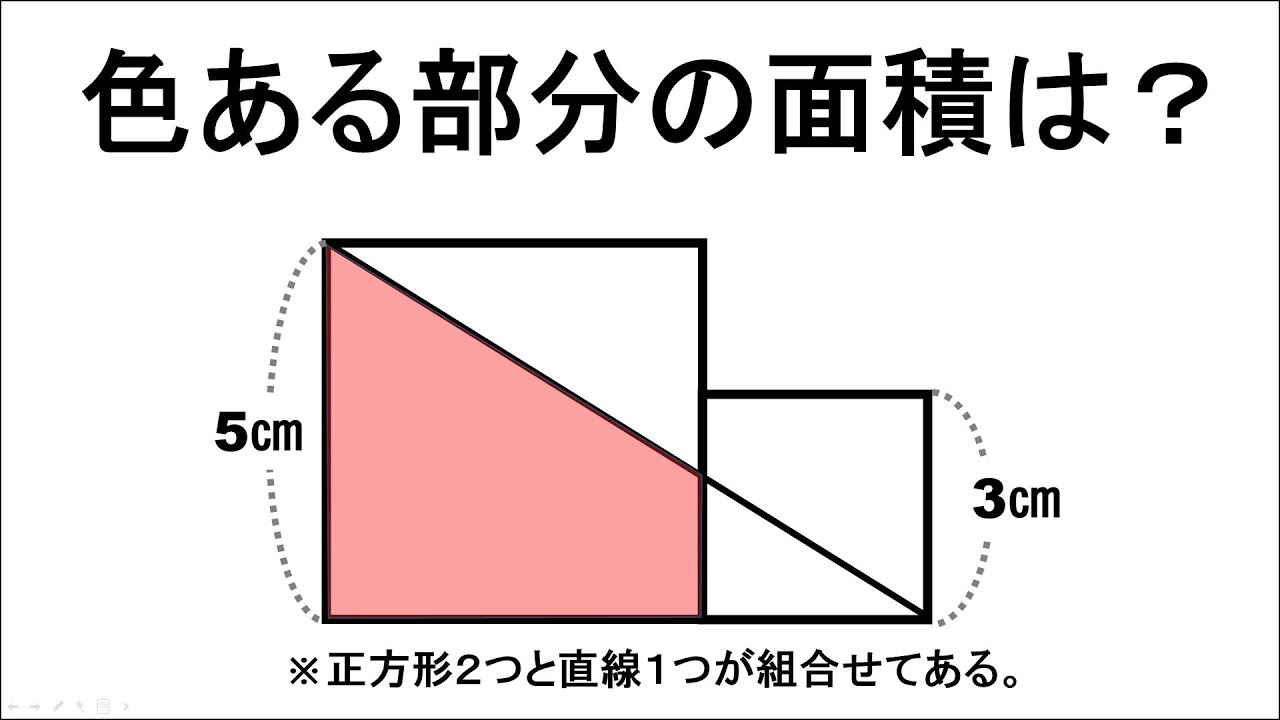
問題文全文(内容文)：
すとぷりの曲で「地球くらいのショートケーキを食べたら」ってあるんですけど，何キロカロリーか解説していきます。

単元： #算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
すとぷりの曲で「地球くらいのショートケーキを食べたら」ってあるんですけど，何キロカロリーか解説していきます。

投稿日：2023.12.31

＜関連動画＞

約数の和　　愛知高校

単元： #計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)

指導講師：数学を数楽に

問題文全文(内容文)：
p,qは素数。積pqの正の約数の和が18のとき
pq=?
愛知高等学校

この動画を見る　

灘中　整数問題

単元： #算数(中学受験)#計算と数の性質#数の性質その他#過去問解説(学校別)#灘中学校

指導講師：鈴木貫太郎

問題文全文(内容文)：
灘中学校過去問題
連続する4つの数(0,1,2,3),(1,2,3,4)~(6,7,8,9)から3つの数を選んで3桁の数を作る。その3桁の数と残りの数を3で割ったときの余りが同じになるものは全部で何個か。

この動画を見る　

【中学受験算数】解けたら天才！？私が解けなかった超難問の正方形問題！！【毎日１題中学受験算数８２】

単元： #算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#灘中学校

指導講師：こばちゃん塾

問題文全文(内容文)：
1⃣左図の正方形2つの面積の合計が58㎠のとき、xは何㎝？

2⃣左図の四角形ABCD、ECFGが、ともに正方形のとき、四角形ABCDの面積は？

3⃣左図の正方形ABCDの1辺の長さは？

＊図は動画内参照

この動画を見る　

【小3算数-15】大きな数と数直線

単元： #算数(中学受験)#計算と数の性質#いろいろな計算

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
算数(大きな数と数直線)

ポイント
数直線は①目もりでいくつふえるかをチェックしよう!

※数直線は動画を参照

この動画を見る　

【受験算数】図形の移動(1)：（練習❶）2点の移動距離の差を考える【予習シリーズ算数・小5下】

単元： #算数(中学受験)#平面図形#図形の移動

教材： #予習シ#予習シ算数・小5下#中学受験教材#図形の移動

指導講師：理数個別チャンネル

問題文全文(内容文)：
右図のような台形ABCDの辺上を、点Pは毎秒4cmの速さでAからCまで、点Qは毎秒1cmの速さでAからDまで、同時に出発してそれぞれ矢印の方向に動きます。次の問に答えなさい。
(1)四角形ABPQが長方形になるのは、2点が出発してから何秒後ですか。
(2)四角形QPCDが平行四辺形になるのは、2点が出発してから何秒後ですか。

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 地球ショートケーキは何キロカロリー？

＜関連動画＞

約数の和 愛知高校

灘中 整数問題

【中学受験算数】解けたら天才！？私が解けなかった超難問の正方形問題！！【毎日１題中学受験算数８２】

【小3算数-15】大きな数と数直線

【受験算数】図形の移動(1)：（練習❶）2点の移動距離の差を考える【予習シリーズ算数・小5下】