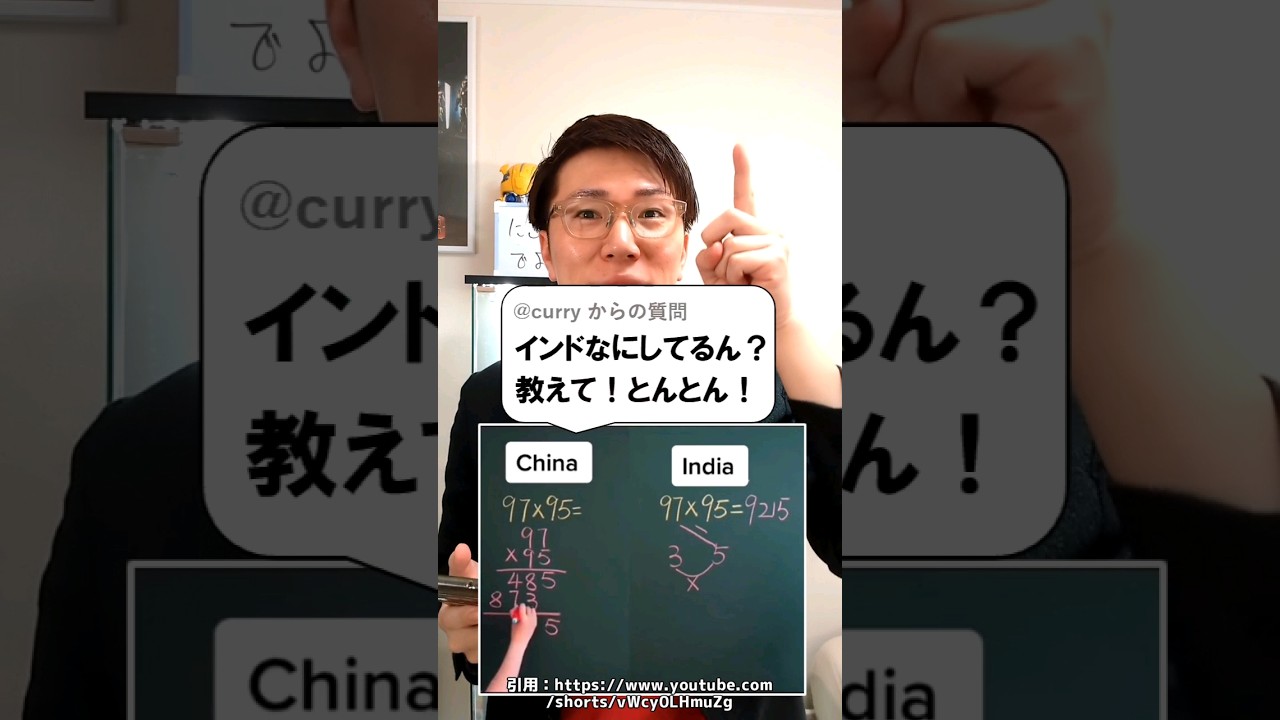
問題文全文(内容文):
64個の小さな立方体を積み重ねて、右図のような大きな立方体を作ります。次に、この大きな立方体の上の面から垂直に、下の面までつきぬける穴を、右図の上の面の4つの黒丸の位置からあけます。他の面からも同じようにして、向かい側の面につきぬける穴を、それぞれ右図の黒丸の位置から開けます。このとき、おのおのの小さな立方体について考えると、1つも穴の開いていない立方体、1方向にだけ穴の開いている立方体、2方向に穴の開いている立方体、3方向に穴の開いている立方体の4種類に分けられます。
これらの個数をそれぞれ求めなさい。
64個の小さな立方体を積み重ねて、右図のような大きな立方体を作ります。次に、この大きな立方体の上の面から垂直に、下の面までつきぬける穴を、右図の上の面の4つの黒丸の位置からあけます。他の面からも同じようにして、向かい側の面につきぬける穴を、それぞれ右図の黒丸の位置から開けます。このとき、おのおのの小さな立方体について考えると、1つも穴の開いていない立方体、1方向にだけ穴の開いている立方体、2方向に穴の開いている立方体、3方向に穴の開いている立方体の4種類に分けられます。
これらの個数をそれぞれ求めなさい。
チャプター:
0:00 オープニング
0:04 説明
単元:
#算数(中学受験)#立体図形#立体図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
受験算数の森
問題文全文(内容文):
64個の小さな立方体を積み重ねて、右図のような大きな立方体を作ります。次に、この大きな立方体の上の面から垂直に、下の面までつきぬける穴を、右図の上の面の4つの黒丸の位置からあけます。他の面からも同じようにして、向かい側の面につきぬける穴を、それぞれ右図の黒丸の位置から開けます。このとき、おのおのの小さな立方体について考えると、1つも穴の開いていない立方体、1方向にだけ穴の開いている立方体、2方向に穴の開いている立方体、3方向に穴の開いている立方体の4種類に分けられます。
これらの個数をそれぞれ求めなさい。
64個の小さな立方体を積み重ねて、右図のような大きな立方体を作ります。次に、この大きな立方体の上の面から垂直に、下の面までつきぬける穴を、右図の上の面の4つの黒丸の位置からあけます。他の面からも同じようにして、向かい側の面につきぬける穴を、それぞれ右図の黒丸の位置から開けます。このとき、おのおのの小さな立方体について考えると、1つも穴の開いていない立方体、1方向にだけ穴の開いている立方体、2方向に穴の開いている立方体、3方向に穴の開いている立方体の4種類に分けられます。
これらの個数をそれぞれ求めなさい。
投稿日:2024.05.13