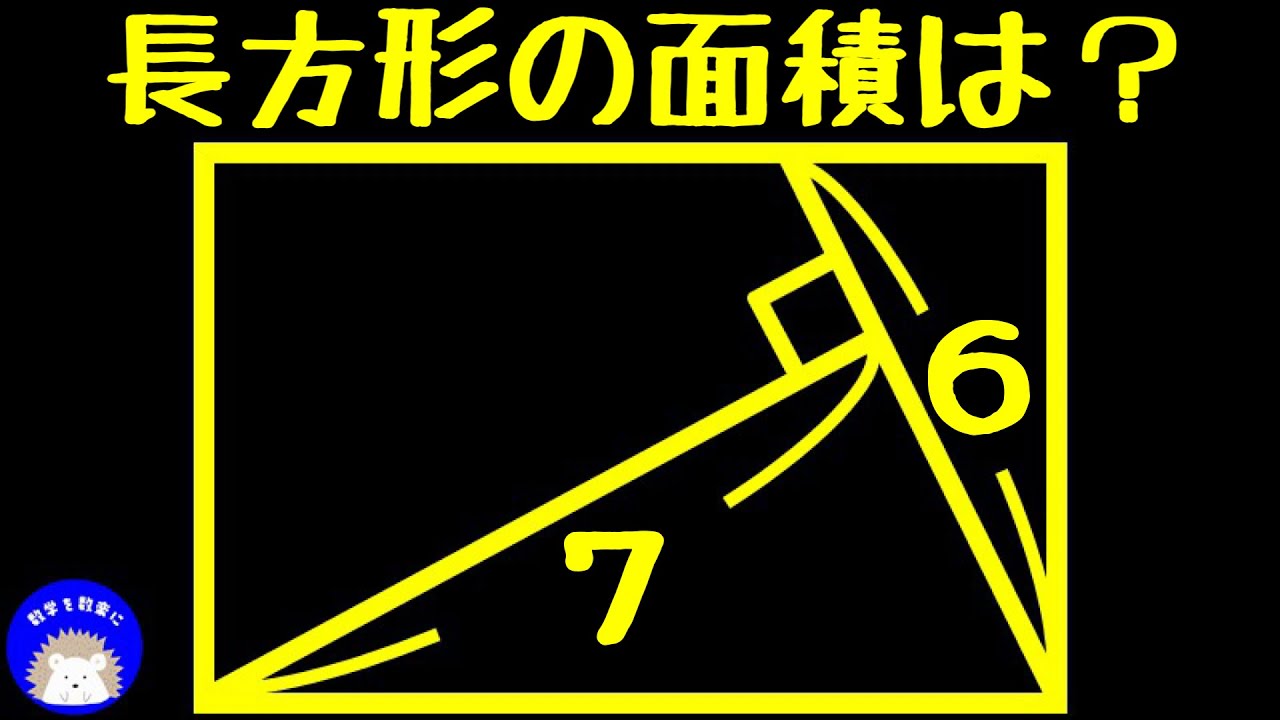
問題文全文(内容文):
理論上ドミノでスカイツリー倒せる...
理論上ドミノでスカイツリー倒せる...
単元:
#算数(中学受験)#立体図形#立体図形その他
指導講師:
【楽しい授業動画】あきとんとん
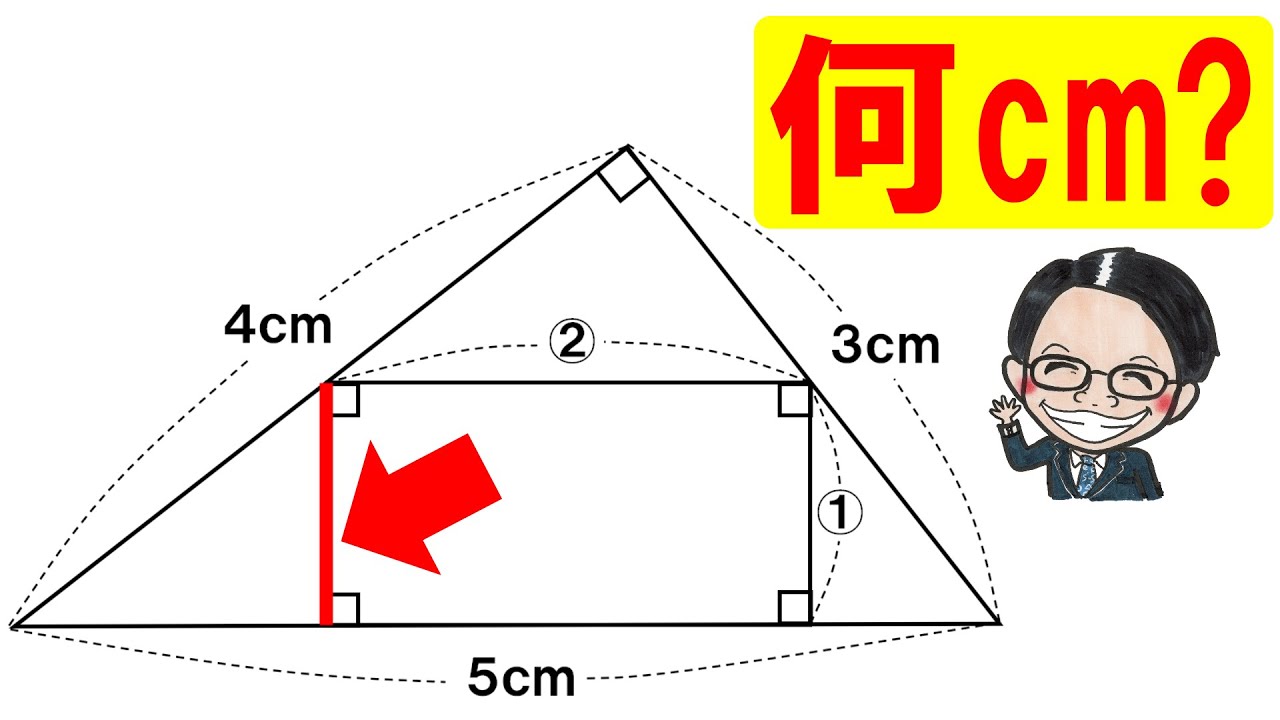
問題文全文(内容文):
理論上ドミノでスカイツリー倒せる...
理論上ドミノでスカイツリー倒せる...
投稿日:2022.07.24