【小３ 算数】 小３－２１ 何十・何百のかけ算 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 計算と数の性質 > いろいろな計算 > 【小３　算数】　　小３－２１　　何十・何百のかけ算

【小３　算数】　　小３－２１　　何十・何百のかけ算

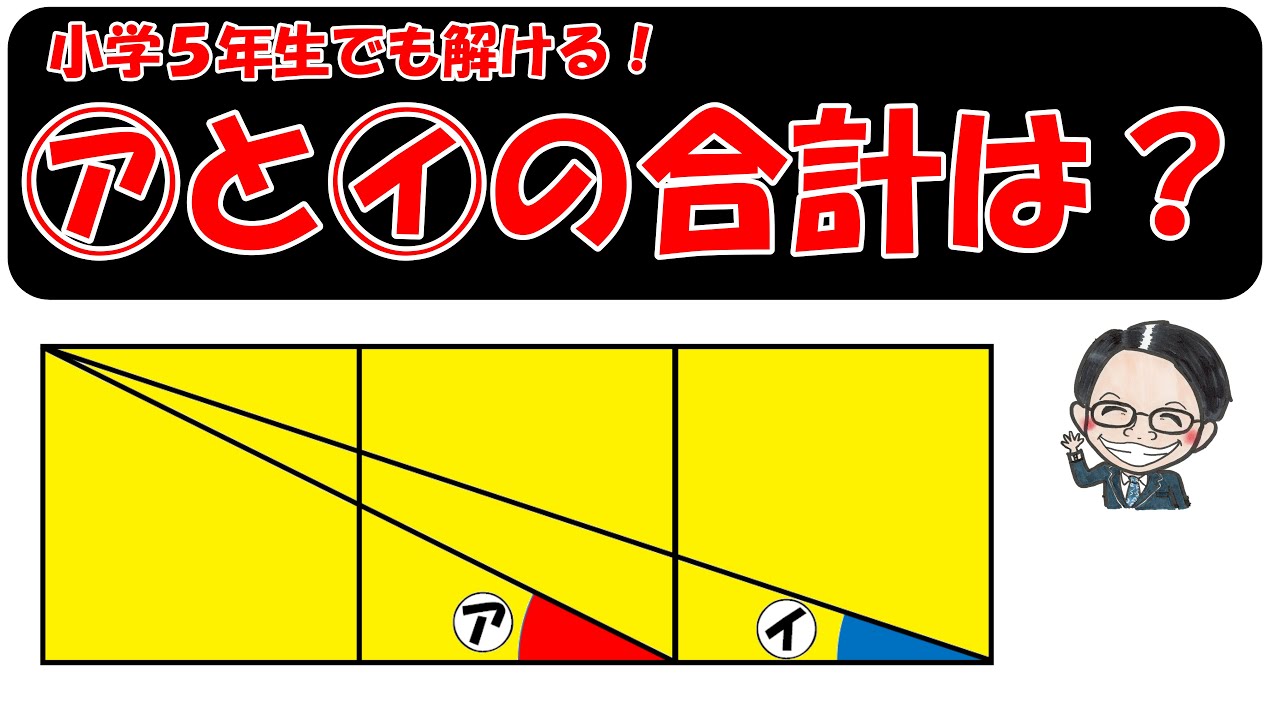
問題文全文(内容文)：
50や700みたいに0のあるかけ算のときは
0に待っていてもらおう！

◎暗算しよう！
①$30 \times 2 =$
②$40 \times 6 =$
③$500 \times 3 =$
④$600 \times 5 =$
⑤$90 \times 3 =$
⑥$30 \times 3 =$
⑦$800 \times 7 =$
⑧$60 \times 7 =$
⑨$5 \times 20 =$
⑩$40 \times 30 =$
⑪$600 \times 60 =$
単元： #算数(中学受験)#計算と数の性質#いろいろな計算
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
50や700みたいに0のあるかけ算のときは
0に待っていてもらおう！

◎暗算しよう！
①$30 \times 2 =$
②$40 \times 6 =$
③$500 \times 3 =$
④$600 \times 5 =$
⑤$90 \times 3 =$
⑥$30 \times 3 =$
⑦$800 \times 7 =$
⑧$60 \times 7 =$
⑨$5 \times 20 =$
⑩$40 \times 30 =$
⑪$600 \times 60 =$
投稿日：2013.09.04

＜関連動画＞

中学受験算数「濃度算の応用①（食塩水の入れ替え）」小学４年生～６年生対象【毎日配信】

アイキャッチ画像
単元： #算数(中学受験)#文章題#売買損益と食塩水
指導講師： 中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
第71回濃度算の応用 ①(食塩水の入れ替え)

例題
2つの容器A,Bがあり、Aには200g、Bには300gの食塩水が入っています。
Aから100gくみ出してBに入れ、よくかき混ぜてBから200gくみ出してAに 入れたら、Aは6%,Bは7%の食塩水になりました。
はじめA.Bに入っていた食塩水の濃度は、それぞれ何% でしたか。
この動画を見る　

4÷5=8が成り立つ理由

アイキャッチ画像
単元： #計算と数の性質#いろいろな計算
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
4÷5=8が成り立つ理由を解説していきます.
この動画を見る　

【中学受験問題に挑戦】　56（”大人”は頭の体操）　等分した三角形の辺の長さ

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： 算数・数学ちゃんねる
問題文全文(内容文)：
等分した三角形の辺の長さ問題を解説していきます。
この動画を見る　

規則性　東大寺学園　2021

アイキャッチ画像
単元： #計算と数の性質#数学(中学生)#規則性（周期算・方陣算・数列・日暦算・N進法）#高校入試過去問(数学)
指導講師： 数学を数楽に
問題文全文(内容文)：
2021は上から何段目の左から何番目？
＊図は動画内参照

2021東大寺学園高等学校
この動画を見る　

【受験算数】慶應義塾中等部2018第3問(1)

アイキャッチ画像
単元： #算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#慶應義塾中等部
指導講師： 理数個別チャンネル
問題文全文(内容文)：
長方形を対角線で折り返しました。角アと角イが8：5である時、角Xの大きさは▢°である。
この動画を見る　
PAGE TOP