とある男が授業をしてみた
とある男が授業をしてみた
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【数Ⅲ-139】部分積分①
単元：
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(部分積分①)
Q.次の不定積分を求めよ
①$\int xcosxdx$
➁$\int (x+3)cos2xdx$
③$\int x^2 sinxdx$
この動画を見る
数Ⅲ(部分積分①)
Q.次の不定積分を求めよ
①$\int xcosxdx$
➁$\int (x+3)cos2xdx$
③$\int x^2 sinxdx$
【数Ⅲ-138】置換積分③
単元：
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(置換積分③)
Q.次の不定積分を求めよ
①$\int (2x+1)(x^2+x-3)^3dx$
➁$\int \frac{2x}{\sqrt{x^2-4}}dx$
③$\int \frac{tanx}{cosx}dx$
この動画を見る
数Ⅲ(置換積分③)
Q.次の不定積分を求めよ
①$\int (2x+1)(x^2+x-3)^3dx$
➁$\int \frac{2x}{\sqrt{x^2-4}}dx$
③$\int \frac{tanx}{cosx}dx$
【数Ⅲ-137】置換積分②
単元：
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
Q,次の不定積分を求めよ
①$\int x\sqrt{x+1}dx$
➁$\int(2x-1)(x+1)^3dx$
③$\int \frac{x}{\sqrt{2x+1}}dx$
この動画を見る
Q,次の不定積分を求めよ
①$\int x\sqrt{x+1}dx$
➁$\int(2x-1)(x+1)^3dx$
③$\int \frac{x}{\sqrt{2x+1}}dx$
【数Ⅲ-136】置換積分①
単元：
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(置換積分①)
Q.次の不定積分を求めよ
①$\int(4x-1)^3dx$
➁$\int sin(2θ +\frac{\pi}{3})dθ$
③$\int^3 \sqrt{2-x}dx$
④$\int \frac{1}{1-3x}dx$
⑤$\int \frac{2x}{x^2+1}dx$
⑥$\int \frac{1}{tanx}dx$
この動画を見る
数Ⅲ(置換積分①)
Q.次の不定積分を求めよ
①$\int(4x-1)^3dx$
➁$\int sin(2θ +\frac{\pi}{3})dθ$
③$\int^3 \sqrt{2-x}dx$
④$\int \frac{1}{1-3x}dx$
⑤$\int \frac{2x}{x^2+1}dx$
⑥$\int \frac{1}{tanx}dx$
【数Ⅲ-135】不定積分③(指数関数編)
単元：
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(不定積分③・指数関数編)
③$\int (4e^x+3)dx$
④$\int (5^x-2^x)dx$
⑤$\int e^{3x}dx$
この動画を見る
数Ⅲ(不定積分③・指数関数編)
③$\int (4e^x+3)dx$
④$\int (5^x-2^x)dx$
⑤$\int e^{3x}dx$
【数Ⅲ-134】不定積分②(三角関数編)
単元：
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(不定積分➁・三角関数編)
⑤$\int (4sin x-3cos x)dx$
⑥$\int \frac{cos^3x+5}{cos^2x}dx$
⑦$\int \frac{1}{tan^2x}dx$
この動画を見る
数Ⅲ(不定積分➁・三角関数編)
⑤$\int (4sin x-3cos x)dx$
⑥$\int \frac{cos^3x+5}{cos^2x}dx$
⑦$\int \frac{1}{tan^2x}dx$
【数Ⅲ-133】不定積分①(準備運動編)
単元：
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(不定積分①・準備運動編)
Q.次の不定積分を求めよ
①$\int 5x^2dx$
➁$\int (8x^3+x^2-6x+5)dx$
③$\int (\frac{1}{x^3}-\sqrt{x})dx$
④$\int (\frac{6x^4-3}{x^2})dx$
⑤$\int \frac{(x-1)^2}{x^3}dx$
⑥$\int (\frac{x-2}{x})^2dx$
この動画を見る
数Ⅲ(不定積分①・準備運動編)
Q.次の不定積分を求めよ
①$\int 5x^2dx$
➁$\int (8x^3+x^2-6x+5)dx$
③$\int (\frac{1}{x^3}-\sqrt{x})dx$
④$\int (\frac{6x^4-3}{x^2})dx$
⑤$\int \frac{(x-1)^2}{x^3}dx$
⑥$\int (\frac{x-2}{x})^2dx$
【数Ⅲ-132】近似式
単元：
#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(近似式)
$x≒0$のとき、次の関数について1次の近似式を求めよ。
①$\sqrt{1+3x}$
➁$\log (e+x)$
③$sin31°$の近似値を、1次の近似式を用いて少数第3位まで求めよ。
ただし$\sqrt{3}＝1.73,\pi=3.14$とする。
この動画を見る
数Ⅲ(近似式)
$x≒0$のとき、次の関数について1次の近似式を求めよ。
①$\sqrt{1+3x}$
➁$\log (e+x)$
③$sin31°$の近似値を、1次の近似式を用いて少数第3位まで求めよ。
ただし$\sqrt{3}＝1.73,\pi=3.14$とする。
【数Ⅲ-131】いろいろな量の変化率
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(いろいろな量の変化率)
①毎秒$3cm^2$の割合で表面積が増加している球がある。
この球の半径が$4cm$になった瞬間における体積の変化率を求めよ。
②右の図のような直円錐の容器に、毎秒$3cm^3$の割合で水を注ぐ。
水面の高さが$6cm$になったときの水面の上昇する速度を求めよ。
この動画を見る
数Ⅲ(いろいろな量の変化率)
①毎秒$3cm^2$の割合で表面積が増加している球がある。
この球の半径が$4cm$になった瞬間における体積の変化率を求めよ。
②右の図のような直円錐の容器に、毎秒$3cm^3$の割合で水を注ぐ。
水面の高さが$6cm$になったときの水面の上昇する速度を求めよ。
【数Ⅲ-130】速度と加速度③(円運動編)
単元：
#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(速度と加速度③・円運動編)
$o$が原点の座標平面上の動点$P$の時刻$t$における位置が$x=3\cos2t$、$y=3\sin2t$で表されるとき、次の問いに答えよ。
①速度$\vec{v},$加速度$\vec{a}$を求めよ。
②$\overrightarrow{OP} \perp \vec{v},\vec{v}\perp \vec{a}$を示せ。
この動画を見る
数Ⅲ(速度と加速度③・円運動編)
$o$が原点の座標平面上の動点$P$の時刻$t$における位置が$x=3\cos2t$、$y=3\sin2t$で表されるとき、次の問いに答えよ。
①速度$\vec{v},$加速度$\vec{a}$を求めよ。
②$\overrightarrow{OP} \perp \vec{v},\vec{v}\perp \vec{a}$を示せ。
【数Ⅲ-129】速度と加速度②(平面上の点の運動編)
単元：
#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(速度と加速度➁・平面上の点の運動編)
①座標平面上を運動する点$P(x,y)$の時刻$t$における座標が$x=e^t\cos t$、$y=e^t\sin t$であるとき、
点$P$の時刻$t$における速さ$\vec{v}$と加速度$\vec{a}$の大きさをそれぞれ求めよ
この動画を見る
数Ⅲ(速度と加速度➁・平面上の点の運動編)
①座標平面上を運動する点$P(x,y)$の時刻$t$における座標が$x=e^t\cos t$、$y=e^t\sin t$であるとき、
点$P$の時刻$t$における速さ$\vec{v}$と加速度$\vec{a}$の大きさをそれぞれ求めよ
【数Ⅲ-128】速度と加速度①(直線上の点の運動編)
単元：
#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(速度と加速度①・直線上の運動編)
地上から真上に投げ上げた物体の時刻$t$における高さが$h(t)=40t-5t^2$で表されるとき、次の問いに答えよ。
①速度$v(t)$、加速度$a(t)$を求めよ。
②最高到達点の高さを求めよ。
③地上に落下するときの速度を求めよ。
この動画を見る
数Ⅲ(速度と加速度①・直線上の運動編)
地上から真上に投げ上げた物体の時刻$t$における高さが$h(t)=40t-5t^2$で表されるとき、次の問いに答えよ。
①速度$v(t)$、加速度$a(t)$を求めよ。
②最高到達点の高さを求めよ。
③地上に落下するときの速度を求めよ。
【数Ⅲ-127】微分の方程式への応用
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(微分の方程式への応用)
$a$を定数とするとき、次の$x$についての方程式の異なる実数解の個数を調べよ。
①$e^x=x+a$
②$2x^3-ax^2+1$
この動画を見る
数Ⅲ(微分の方程式への応用)
$a$を定数とするとき、次の$x$についての方程式の異なる実数解の個数を調べよ。
①$e^x=x+a$
②$2x^3-ax^2+1$
【数Ⅲ-126】微分の不等式への応用②
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(微分の不等式への応用➁)
$x\gt0$のとき、不等式$\sqrt{1+x}\gt1+\frac{1}{2}x-\frac{1}{8}x^2$を証明せよ
この動画を見る
数Ⅲ(微分の不等式への応用➁)
$x\gt0$のとき、不等式$\sqrt{1+x}\gt1+\frac{1}{2}x-\frac{1}{8}x^2$を証明せよ
【数Ⅲ-125】微分の不等式への応用①
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数Ⅲ(微分の不等式への応用①)
①$x\gt1$のとき、不等式$2\sqrt{x}\gt\log x$を証明せよ
➁$x\gt1$のとき、不等式$\log x\leqq\frac{x}{e}$を証明せよ
この動画を見る
数Ⅲ(微分の不等式への応用①)
①$x\gt1$のとき、不等式$2\sqrt{x}\gt\log x$を証明せよ
➁$x\gt1$のとき、不等式$\log x\leqq\frac{x}{e}$を証明せよ
リクエスト頂いた規則性やっていきましょう【中学受験】
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
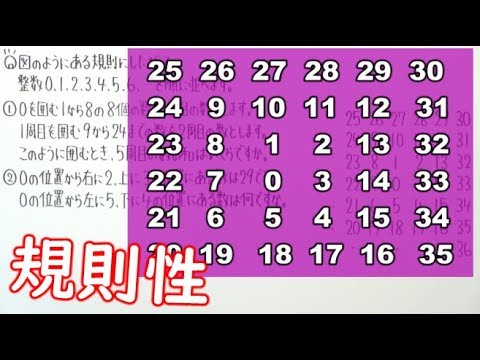
図のようにある規則にしたがって、整数0.1.2.3.4.5.6...を順に並べます。
①
0を囲む1から8の8個の数を1周目の数とします。
1周目を囲む9から24までの数を2周目の数とします。
このように囲むとき、5周目の数の和はいくらですか。
②
0の位置から右に2、上に3の位置にある数は29です。
0の位置から左に5、下に4の位置にある数は何ですか。
この動画を見る
図のようにある規則にしたがって、整数0.1.2.3.4.5.6...を順に並べます。
①
0を囲む1から8の8個の数を1周目の数とします。
1周目を囲む9から24までの数を2周目の数とします。
このように囲むとき、5周目の数の和はいくらですか。
②
0の位置から右に2、上に3の位置にある数は29です。
0の位置から左に5、下に4の位置にある数は何ですか。
中学入試の問題をやってみます【お試し】
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$12×(\frac{1}{2}-\frac{1}{3})-(\frac{1}{2}\div 0.75-\frac{4}{9})×9$
②$93-89+83-71+59-53+50-47+41-29+17-11+7$
③$(954-459-25×16+0.4)\div(\frac{1}{12}+\frac{1}{84}+\frac{1}{210}) $
④$(0.375×24+2.5×0.625×16)×19-25×12-125×16-1.4×190$
⑤$1×1×1+3+5+3×3×3+13+15+17+19+5×5×5+31+33+35+37+39+41$
この動画を見る
①$12×(\frac{1}{2}-\frac{1}{3})-(\frac{1}{2}\div 0.75-\frac{4}{9})×9$
②$93-89+83-71+59-53+50-47+41-29+17-11+7$
③$(954-459-25×16+0.4)\div(\frac{1}{12}+\frac{1}{84}+\frac{1}{210}) $
④$(0.375×24+2.5×0.625×16)×19-25×12-125×16-1.4×190$
⑤$1×1×1+3+5+3×3×3+13+15+17+19+5×5×5+31+33+35+37+39+41$
【理科】中2-1 炭酸水素ナトリウムを熱する実験 (撮り直ししました)
単元：
#理科(中学生)#化学
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
理科(炭酸水素ナトリウムを熱する実験)
ポイント
炭酸水素ナトリウム→①(個体)+➁(液体)＋③(気体)
このように1種類の物質が2種類以上の別の物質にわかれる変化を④という
<実験するときの3つの注意点〉
【1】⑤ために試験管の口を底より少し下げておく。
【2】⑥ために火を消す前に⑦から出しておく。
【3】最初は⑧ので1本目は使わない。
集めた気体の試験管に火のついた線香をいれると⑨、石灰水を入れてふると➉。
出てきた液体に⑪紙をつけると⑫色になる。
炭酸水素ナトリウムと熱した後の物質に⑬溶液を反応させると、それぞれ⑭色、⑮色になる。
この動画を見る
理科(炭酸水素ナトリウムを熱する実験)
ポイント
炭酸水素ナトリウム→①(個体)+➁(液体)＋③(気体)
このように1種類の物質が2種類以上の別の物質にわかれる変化を④という
<実験するときの3つの注意点〉
【1】⑤ために試験管の口を底より少し下げておく。
【2】⑥ために火を消す前に⑦から出しておく。
【3】最初は⑧ので1本目は使わない。
集めた気体の試験管に火のついた線香をいれると⑨、石灰水を入れてふると➉。
出てきた液体に⑪紙をつけると⑫色になる。
炭酸水素ナトリウムと熱した後の物質に⑬溶液を反応させると、それぞれ⑭色、⑮色になる。
【高校受験対策】数学-死守36
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#平方根
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守36
①$5+4 \times 6$を計算せよ
②$\frac{9}{5}\div 0.8-\frac{1}{2}$を計算せよ
③$\sqrt{60}\div \sqrt{5}+\sqrt{27}$を計算せよ
④比例式$3:4=(x-6):8$について$x$の値を求めよ。
⑤$3x^2+9x-12$を因数分解せよ。
⑥$n$を50以下の正の整数とするとき、$\sqrt{5n}$の値が整数となるような$n$の値をすべて求めよ。
⑦次の口と△にどんな自然数を入れても、計算の結果がつねに自然数 になるものはどれか。
下のア~エの中からあてはまるものをすべて答えよ。
ア 口＋△
イ 口-△
ウ 口×△
エ 口÷△
⑧大小2つのさいころを同時に投げる。
大きいさいころの出た目の数を$x$座標、小さいさいころの出た目の数を$y$座標とする点を$P(x,y)$とするとき、点$P$が1次関数$y=-x+8$のグラフ上の点となる確率を求めよ。
⑨右の図は半径$rcm$の球を切断して できた半球で、切断面の円周の長さは$4\pi cm$であった。
このとき$r$の値を求めよ。
また、この半球の体積は何$cm^3$か。 ただし$\pi$は円周率とする。
この動画を見る
高校受験対策・死守36
①$5+4 \times 6$を計算せよ
②$\frac{9}{5}\div 0.8-\frac{1}{2}$を計算せよ
③$\sqrt{60}\div \sqrt{5}+\sqrt{27}$を計算せよ
④比例式$3:4=(x-6):8$について$x$の値を求めよ。
⑤$3x^2+9x-12$を因数分解せよ。
⑥$n$を50以下の正の整数とするとき、$\sqrt{5n}$の値が整数となるような$n$の値をすべて求めよ。
⑦次の口と△にどんな自然数を入れても、計算の結果がつねに自然数 になるものはどれか。
下のア~エの中からあてはまるものをすべて答えよ。
ア 口＋△
イ 口-△
ウ 口×△
エ 口÷△
⑧大小2つのさいころを同時に投げる。
大きいさいころの出た目の数を$x$座標、小さいさいころの出た目の数を$y$座標とする点を$P(x,y)$とするとき、点$P$が1次関数$y=-x+8$のグラフ上の点となる確率を求めよ。
⑨右の図は半径$rcm$の球を切断して できた半球で、切断面の円周の長さは$4\pi cm$であった。
このとき$r$の値を求めよ。
また、この半球の体積は何$cm^3$か。 ただし$\pi$は円周率とする。
【高校受験対策】英語/2時間目
単元：
#中3英語#不定詞(疑問詞+to,It～for to,ask(tell,want)O to,too～to,enough～to,not to)#分詞(現在分詞の形容詞的用法、過去分詞の形容詞的用法)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①
A: Can you (to. think. good. of something) bring to the party?
B: How about bringing pizza?
➁
A: Will you carry this desk to the next room with me?
B: OK, but it (big. to. may, too, go. be) through the door.
③
I want ( ) to enjoy Japanese food.
1→ many people visit Japan
2→ Japan visiting many people
3→ many people visiting Japan
4→ many visiting Japan people
この動画を見る
①
A: Can you (to. think. good. of something) bring to the party?
B: How about bringing pizza?
➁
A: Will you carry this desk to the next room with me?
B: OK, but it (big. to. may, too, go. be) through the door.
③
I want ( ) to enjoy Japanese food.
1→ many people visit Japan
2→ Japan visiting many people
3→ many people visiting Japan
4→ many visiting Japan people
【高校受験対策】数学-図形25
単元：
#数学(中学生)#中３数学#三平方の定理
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
1辺の長さが$4cm$の正方形$ABCD$がある。同1・間2に答えなさい。
問1
右の図のように、点$P$が$A$を出発し、正方形$ABCD$の周上を、 毎秒$1cm$の速さで$B$、$C$を通って$D$まで移動する。
(1)(2)に 答えなさい。
(1)点$P$が$A$を出発してから6秒後の線分$AP$の長さを求めなさい。
(2) 点$P$が$CD$上にあり、四角形$ABCP$の面積が$10cm^2$となるのは、点$P$が$A$を出発してから何秒後か、求めなさい。
問2
下の図のように、正方形$ABCD$の外側に、正三角形$ABE$と$\angle CBF=90°$の直角三角形$BCF$をつくる。
辺$CF$の中点を$M$とし、$BF=4\sqrt{3}cm$であるとき、(1)・(2)に答えなさい。
(1)$△BDE$の面積を求めなさい
(2)線分$BM$と線分$DF$の交点を$Q$とするとき、$BQ:QM$を求めなさい。
この動画を見る
1辺の長さが$4cm$の正方形$ABCD$がある。同1・間2に答えなさい。
問1
右の図のように、点$P$が$A$を出発し、正方形$ABCD$の周上を、 毎秒$1cm$の速さで$B$、$C$を通って$D$まで移動する。
(1)(2)に 答えなさい。
(1)点$P$が$A$を出発してから6秒後の線分$AP$の長さを求めなさい。
(2) 点$P$が$CD$上にあり、四角形$ABCP$の面積が$10cm^2$となるのは、点$P$が$A$を出発してから何秒後か、求めなさい。
問2
下の図のように、正方形$ABCD$の外側に、正三角形$ABE$と$\angle CBF=90°$の直角三角形$BCF$をつくる。
辺$CF$の中点を$M$とし、$BF=4\sqrt{3}cm$であるとき、(1)・(2)に答えなさい。
(1)$△BDE$の面積を求めなさい
(2)線分$BM$と線分$DF$の交点を$Q$とするとき、$BQ:QM$を求めなさい。
【高校受験対策】数学-関数41
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、関数$y=\frac{1}{2}x^2$のグラフ上に2点$A$・$B$があり、点$A$の$x$座標は$-3$、点$B$は点$A$と$y$軸について対称である。
このとき次の問いに答えなさい。
問1
関数$y=\frac{1}{2}x^2$について、$x$の変域が$-3 \leqq x \leqq 4$のときの$y$の変域を求めなさい。
問2
$y$軸上に点$C$を、四角形$OBCA$がひし形となるようにとる。
このとき次の問いに答えなさい。
(1) 直線$AC$の式を求めなさい。
(2) 線分$AC$上に点$D$をとる。$△ODA$と四角形$OBCA$の面積比が$1:4$となるとき、点$D$の座標を求 めなさい。
この動画を見る
右の図のように、関数$y=\frac{1}{2}x^2$のグラフ上に2点$A$・$B$があり、点$A$の$x$座標は$-3$、点$B$は点$A$と$y$軸について対称である。
このとき次の問いに答えなさい。
問1
関数$y=\frac{1}{2}x^2$について、$x$の変域が$-3 \leqq x \leqq 4$のときの$y$の変域を求めなさい。
問2
$y$軸上に点$C$を、四角形$OBCA$がひし形となるようにとる。
このとき次の問いに答えなさい。
(1) 直線$AC$の式を求めなさい。
(2) 線分$AC$上に点$D$をとる。$△ODA$と四角形$OBCA$の面積比が$1:4$となるとき、点$D$の座標を求 めなさい。
【高校受験対策】数学-文章題6
単元：
#数学(中学生)#中１数学#文字と式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
2つの自然数$a$、$b$に対して、$a$を$b$で割ったときの商を$[a☆b]$、余りを$[a◎b]$で表すこととする。
ただし、商は0以上の整数とする。
例えば、20を3で割ると商が6、余りが2であるから、$[20☆3]=6$、$[20◎3]=2$となる。
また、 3を5で割ると商が0、余りが3であるから、$[3☆5]=0$、$[3◎5]=3$となる。
このとき次の間1~間4に答えなさい。
問1 次の(ア)、(イ)に入る数をそれぞれ書きなさい。
$[37☆7]=$(ア)、$[37◎7]=$(イ)
問2 $[a☆7]=7$を成り立たせる自然数は全部で何個あるか、求めなさい。
問3 $[a☆14]=3$・・①、$[a◎7]=3$・・➁とするとき、①、②をともに成り立たせる自然数$a$をすべて求めなさい。
問4 $[a◎3]=1$・・①、$[a◎4]=3$・・➁とするとき、①、②をともに成り立たせる自然数$a$のうち、2桁の自然数は全部で何個あるか求めなさい。
この動画を見る
2つの自然数$a$、$b$に対して、$a$を$b$で割ったときの商を$[a☆b]$、余りを$[a◎b]$で表すこととする。
ただし、商は0以上の整数とする。
例えば、20を3で割ると商が6、余りが2であるから、$[20☆3]=6$、$[20◎3]=2$となる。
また、 3を5で割ると商が0、余りが3であるから、$[3☆5]=0$、$[3◎5]=3$となる。
このとき次の間1~間4に答えなさい。
問1 次の(ア)、(イ)に入る数をそれぞれ書きなさい。
$[37☆7]=$(ア)、$[37◎7]=$(イ)
問2 $[a☆7]=7$を成り立たせる自然数は全部で何個あるか、求めなさい。
問3 $[a☆14]=3$・・①、$[a◎7]=3$・・➁とするとき、①、②をともに成り立たせる自然数$a$をすべて求めなさい。
問4 $[a◎3]=1$・・①、$[a◎4]=3$・・➁とするとき、①、②をともに成り立たせる自然数$a$のうち、2桁の自然数は全部で何個あるか求めなさい。
【高校受験対策】数学-関数40
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
下の図のように、関数$y=\frac{1}{3}x^2$のグラフ上に2点$A$、$B$がある。
点Ａの$x$座標は$-6$、点$B$の$x$座標は$3$であり、2点$A$、$B$を通る直線と$x$軸との交点を$C$とする。
このとき、次の間1~問6に答えなさい。
問1 点$B$の$y$座標を求めなさい。
問2 関数$y=\frac{1}{3}x^2$について、 $x$の変域が$-6 \leqq x \leqq 3$のときの$y$の変域を求めなさい。
問3 2点$A$、$B$を通る直線の式を求めなさい。
問4 点$C$の座標を求めなさい。
問5 $△OAB$の面積を求めなさい。
問6 $y=\frac{1}{3}x^2$のグラフ上に点$P$にある。$△POC$の面積が$△OAB$の面積と等しくなるような点$P$の$x$座標をすべて求めなさい。
この動画を見る
下の図のように、関数$y=\frac{1}{3}x^2$のグラフ上に2点$A$、$B$がある。
点Ａの$x$座標は$-6$、点$B$の$x$座標は$3$であり、2点$A$、$B$を通る直線と$x$軸との交点を$C$とする。
このとき、次の間1~問6に答えなさい。
問1 点$B$の$y$座標を求めなさい。
問2 関数$y=\frac{1}{3}x^2$について、 $x$の変域が$-6 \leqq x \leqq 3$のときの$y$の変域を求めなさい。
問3 2点$A$、$B$を通る直線の式を求めなさい。
問4 点$C$の座標を求めなさい。
問5 $△OAB$の面積を求めなさい。
問6 $y=\frac{1}{3}x^2$のグラフ上に点$P$にある。$△POC$の面積が$△OAB$の面積と等しくなるような点$P$の$x$座標をすべて求めなさい。
【高校受験対策】数学-規則性6
単元：
#数学(中学生)#中２数学#連立方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
図1のような、縦$acm$、横$bcm$の長方形の紙がある。
この長方形の紙に対して次のような【操作】を行う。ただし$a$、$b$は正の整数であり、$a \lt b$とする。
【操作】
長方形の紙から短い方の辺を1辺とする正方形を切り取る。
残った四角形が正方形でない場合には、その四角形からさらに同様の方法で正方形を切り取り、残った四角形が正方形になるまで繰り返す。
例えば、図2のように、$a$=3、$ b$=4の長方形の紙に対して【操作】を行うと、1辺3cmの正方形の紙が1枚、1辺1cmの正方形の紙が3枚、全部で4枚の正方形ができる。
このとき次の問1、間2、間3、間4に答えなさい。
問1
$a$=4、$b$=6の長方形の紙に対して【操作】を行ったとき、できた正方形のうち最も小さい正方形の 1辺の長さを求めなさい。
問2
$n$を正の整数とする。$a=n$、$b=3n+1$の長方形の紙に対して【操作】を行ったとき、正方形は全部で何枚できるか。$n$を用いて表しなさい。
問3
ある長方形の紙に対して【操作】を行ったところ、3種類の大きさの異なる正方形が全部で4枚できた。
これらの正方形は、1辺の長さが長い順に、12cmの正方形が1枚、$x$cmの正方形が1枚、$y$cmの正方形が2枚であった。
このとき、$x$、$y$の連立方程式をつくり、$x$、$y$の値を求めなさい。ただし、 途中の計算も書くこと。
問４
$b=56$の長方形の紙に対して【操作】を行ったところ、3種類の大きさの異なる正方形が全で5枚できた。このとき考えられる$a$の値をすべて求めなさい。
この動画を見る
図1のような、縦$acm$、横$bcm$の長方形の紙がある。
この長方形の紙に対して次のような【操作】を行う。ただし$a$、$b$は正の整数であり、$a \lt b$とする。
【操作】
長方形の紙から短い方の辺を1辺とする正方形を切り取る。
残った四角形が正方形でない場合には、その四角形からさらに同様の方法で正方形を切り取り、残った四角形が正方形になるまで繰り返す。
例えば、図2のように、$a$=3、$ b$=4の長方形の紙に対して【操作】を行うと、1辺3cmの正方形の紙が1枚、1辺1cmの正方形の紙が3枚、全部で4枚の正方形ができる。
このとき次の問1、間2、間3、間4に答えなさい。
問1
$a$=4、$b$=6の長方形の紙に対して【操作】を行ったとき、できた正方形のうち最も小さい正方形の 1辺の長さを求めなさい。
問2
$n$を正の整数とする。$a=n$、$b=3n+1$の長方形の紙に対して【操作】を行ったとき、正方形は全部で何枚できるか。$n$を用いて表しなさい。
問3
ある長方形の紙に対して【操作】を行ったところ、3種類の大きさの異なる正方形が全部で4枚できた。
これらの正方形は、1辺の長さが長い順に、12cmの正方形が1枚、$x$cmの正方形が1枚、$y$cmの正方形が2枚であった。
このとき、$x$、$y$の連立方程式をつくり、$x$、$y$の値を求めなさい。ただし、 途中の計算も書くこと。
問４
$b=56$の長方形の紙に対して【操作】を行ったところ、3種類の大きさの異なる正方形が全で5枚できた。このとき考えられる$a$の値をすべて求めなさい。
【高校受験対策】数学-関数39
単元：
#数学(中学生)#中２数学#1次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
和夫さんは、本を返却するために家から1800m離れた図書館へ行った。和夫さんは午後4時に家を出発し、毎分180mの速さで5分間走った後、毎分90mの速さで10分間歩いて、図書館に到着した。
その後、本を返却してしばらくたってから図書館を出発し、家へ毎分100mの速さで歩いて帰ったところ、午後4時45分に到着した。
次の図は、午後4時$x$分における家からの道のりを$y$mとして、$x$と$y$の関係をグラフに表したものである。
次の間1~間4に答えなさい。
問1
和夫さんは午後4時3分に郵便局の前を通った。家から郵便局の前までの道のりを求めなさい。
問2
和夫さんが図書館へ行く途中で、歩き始めてから図書館に着くまでの$x$と$y$の関係を式で表しなさ い。ただし、$x$の変域を求める必要はありません。
間3
和夫さんが図書館にいた時間は何分間か、求めなさい。
問4
妹の美紀さんは、午後4時18分に家を出発し、和夫さんと同じ道を通り、図書館へ一定の速さで向かったところ、午後4時33分に和夫さんと出会った。美紀さんが図書館へ向かったときの速さは毎分何mか求めなさい。
この動画を見る
和夫さんは、本を返却するために家から1800m離れた図書館へ行った。和夫さんは午後4時に家を出発し、毎分180mの速さで5分間走った後、毎分90mの速さで10分間歩いて、図書館に到着した。
その後、本を返却してしばらくたってから図書館を出発し、家へ毎分100mの速さで歩いて帰ったところ、午後4時45分に到着した。
次の図は、午後4時$x$分における家からの道のりを$y$mとして、$x$と$y$の関係をグラフに表したものである。
次の間1~間4に答えなさい。
問1
和夫さんは午後4時3分に郵便局の前を通った。家から郵便局の前までの道のりを求めなさい。
問2
和夫さんが図書館へ行く途中で、歩き始めてから図書館に着くまでの$x$と$y$の関係を式で表しなさ い。ただし、$x$の変域を求める必要はありません。
間3
和夫さんが図書館にいた時間は何分間か、求めなさい。
問4
妹の美紀さんは、午後4時18分に家を出発し、和夫さんと同じ道を通り、図書館へ一定の速さで向かったところ、午後4時33分に和夫さんと出会った。美紀さんが図書館へ向かったときの速さは毎分何mか求めなさい。
【高校受験対策】数学-図形24
単元：
#数学(中学生)#中１数学#中３数学#空間図形#三平方の定理
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
問２
右の図の正四面体は、1辺の長さが8cmである。辺$BC$、$CD$の中点をそれぞれ点$P$、Q、 点$Q$から$AP$にひいた垂線と$AP$との交点を$R$とする。次の(1)~(4)に答えなさい。
(1) $AQ$の長さを求めなさい。
(2) $△APQ$の面積を求めなさい。
(3) $QR$の長さを求めなさい。
(4) 三角すい$RBCD$の体積は、正四面体$ABCD$の体積の何倍か、求めなさい
この動画を見る
問２
右の図の正四面体は、1辺の長さが8cmである。辺$BC$、$CD$の中点をそれぞれ点$P$、Q、 点$Q$から$AP$にひいた垂線と$AP$との交点を$R$とする。次の(1)~(4)に答えなさい。
(1) $AQ$の長さを求めなさい。
(2) $△APQ$の面積を求めなさい。
(3) $QR$の長さを求めなさい。
(4) 三角すい$RBCD$の体積は、正四面体$ABCD$の体積の何倍か、求めなさい
【高校受験対策】数学-文章題5
単元：
#数学(中学生)#中２数学#連立方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・文章題5
①
右の記事は、ある中学校の保健委員会が発行した「保健だより」の一部である。
品数が「3品以上」と答えた生徒が、1、2年生あわせて149人であったとき、 朝食を「食べた」と答えた1年生、2年生はそれぞれ何人であったか、方程式をつくって求めなさい。なお途中の計算も書くこと。
②
A市の家庭における1か月あたりの水道料金は、 (水道料金)=(基本料金)+(水の使用量に応じた使用料金)となっています。
使用量が$30m^3$までは、$1m^3$あたりの使用料金が一定であり、使用量が$30m^3$を超えた分の$1m^3$があたりの使用料金は、 使用量が30$m^3$までの$1m^3$あたりの使用料金より80円高くなっています。
A市のある家庭における1ヶ月の水道料金は、使用量が$32m^3$のときは5310円、使用量が$28m^3$のときは4710円でした。 使用量が$30m^3$までの$1m^3$あたりの使用料金を求めなさい。
この動画を見る
高校受験対策・文章題5
①
右の記事は、ある中学校の保健委員会が発行した「保健だより」の一部である。
品数が「3品以上」と答えた生徒が、1、2年生あわせて149人であったとき、 朝食を「食べた」と答えた1年生、2年生はそれぞれ何人であったか、方程式をつくって求めなさい。なお途中の計算も書くこと。
②
A市の家庭における1か月あたりの水道料金は、 (水道料金)=(基本料金)+(水の使用量に応じた使用料金)となっています。
使用量が$30m^3$までは、$1m^3$あたりの使用料金が一定であり、使用量が$30m^3$を超えた分の$1m^3$があたりの使用料金は、 使用量が30$m^3$までの$1m^3$あたりの使用料金より80円高くなっています。
A市のある家庭における1ヶ月の水道料金は、使用量が$32m^3$のときは5310円、使用量が$28m^3$のときは4710円でした。 使用量が$30m^3$までの$1m^3$あたりの使用料金を求めなさい。
【高校受験対策】数学-図形23
単元：
#数学(中学生)#中２数学#中３数学#平行と合同#相似な図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・図形23
右の図において、$△ABC$は$AB=AC$の二等辺三角形であり、 点$D$、$E$はそれぞれ辺$AB$、$AC$の中点である。
また、点$F$は直線DE上の点であり、$EF=DE$である。 このとき次の問1、問2に答えなさい。
問1
$AF=BE$であることを証明しなさい。
問2
線分$BF$と線分$CE$との交点を$G$とする。
$△AEF$において辺AFを底辺とするときの高さを$x$、$△BGE$において辺$BE$を底辺とするときの高さを$y$とするとき、$x:y$を求めなさい。
この動画を見る
高校受験対策・図形23
右の図において、$△ABC$は$AB=AC$の二等辺三角形であり、 点$D$、$E$はそれぞれ辺$AB$、$AC$の中点である。
また、点$F$は直線DE上の点であり、$EF=DE$である。 このとき次の問1、問2に答えなさい。
問1
$AF=BE$であることを証明しなさい。
問2
線分$BF$と線分$CE$との交点を$G$とする。
$△AEF$において辺AFを底辺とするときの高さを$x$、$△BGE$において辺$BE$を底辺とするときの高さを$y$とするとき、$x:y$を求めなさい。
【高校受験対策】英語/1時限目
単元：
#英語(中学生)#中2英語#中3英語#不定詞(名詞的用法・形容詞的用法・副詞的用法)#比較(比較級、最上級、more,mostを使った比較、as~asの文、不規則変化するもの、疑問詞で始まる比較の文)#関係代名詞(主格、目的格、所有格、thatの用法、前置詞＋関係代名詞)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①
A: What season do you like?
B: I like summer. I love swimming in the sea. How about you?
A: I like spring the ( ① ) of all seasons. The flowers are beautiful.
B: I see.
ア much
イ more
ウ better
エ best
➁
A: What will you do tomorrow?
B: I will go to the [borrow, books, to, some, library ]
③
A: I think the writer is smart.
B: Why do you think so?
A: Because the book [is, she, last year, which, wrote] very popular with people of all ages.
この動画を見る
①
A: What season do you like?
B: I like summer. I love swimming in the sea. How about you?
A: I like spring the ( ① ) of all seasons. The flowers are beautiful.
B: I see.
ア much
イ more
ウ better
エ best
➁
A: What will you do tomorrow?
B: I will go to the [borrow, books, to, some, library ]
③
A: I think the writer is smart.
B: Why do you think so?
A: Because the book [is, she, last year, which, wrote] very popular with people of all ages.