 とある男が授業をしてみた
とある男が授業をしてみた
 とある男が授業をしてみた
とある男が授業をしてみた
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【受験対策】 数学-関数④
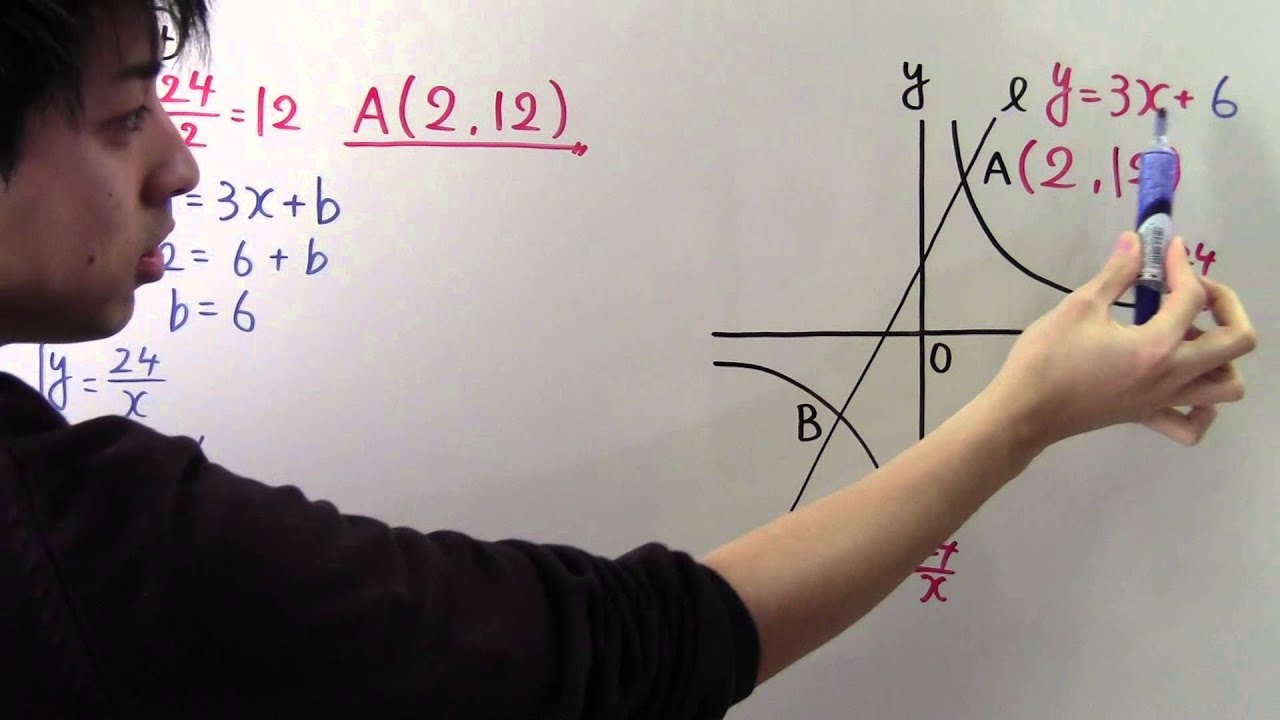
単元:
#数学(中学生)#中1数学#中2数学#比例・反比例#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように、関数$y=\displaystyle \frac{24}{x}$とそのグラフ上の点Aがある。
直線又は点Aを通る傾きが3の直線で、 関数$y=\displaystyle \frac{24}{x}$とのもう一つの交点をBとします。
点Aのx座標が2のとき、次の問いに答えよう。
①点Aの座標は?
②点Bの座標は?
③△OABの面積は?
※図は動画内参照
この動画を見る
右の図のように、関数$y=\displaystyle \frac{24}{x}$とそのグラフ上の点Aがある。
直線又は点Aを通る傾きが3の直線で、 関数$y=\displaystyle \frac{24}{x}$とのもう一つの交点をBとします。
点Aのx座標が2のとき、次の問いに答えよう。
①点Aの座標は?
②点Bの座標は?
③△OABの面積は?
※図は動画内参照
【受験対策】 数学-図形①
単元:
#数学(中学生)#中2数学#中3数学#平行と合同#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
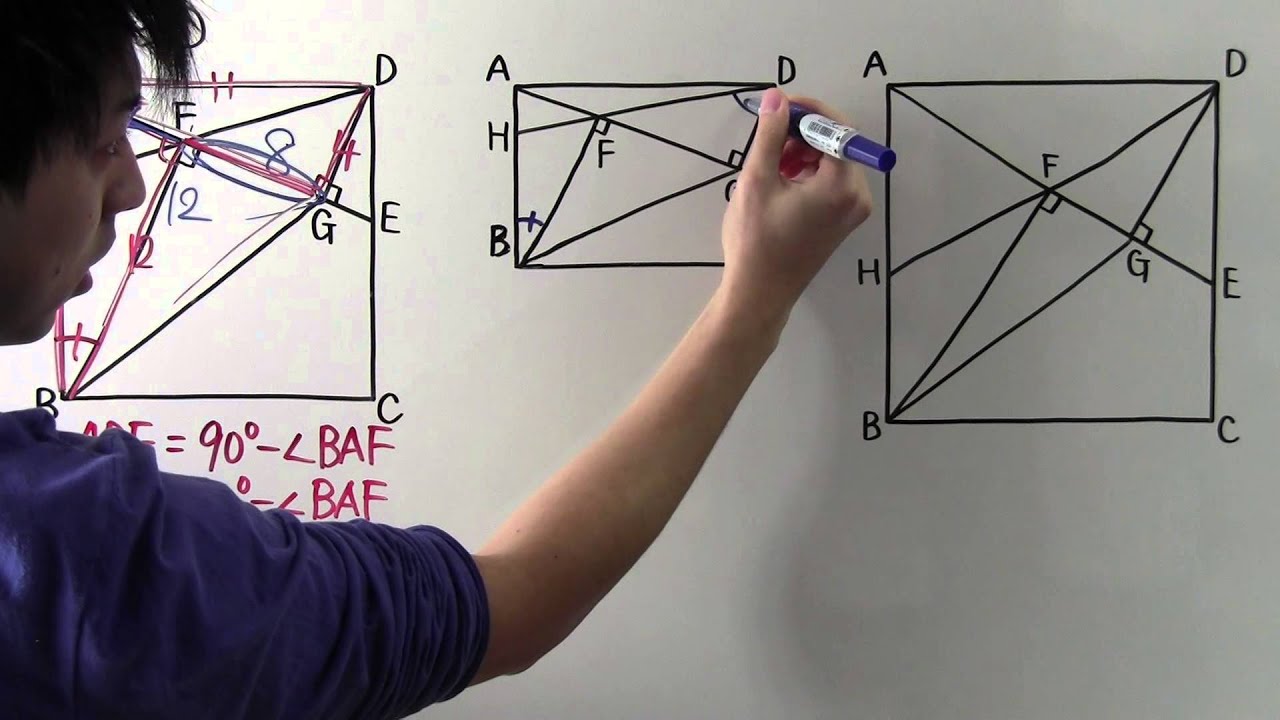
右の図のように、長方形ABCDの辺CD上に点Eをとり、頂点B、DからAEにそれぞれ垂線BF、DGをひきます。
また、DFの延長と辺ABとの交点をHとします。
①$AB=AD,BF12cm$、$DG=4cm$のとき、四角形BFDGの面積は?
②$\angle ABF=\angle FDG、\angle AHF=\angle DFG$のとき、
$AG:AE$を、最も簡単な整数の比で表そう。
※図は動画内参照
この動画を見る
右の図のように、長方形ABCDの辺CD上に点Eをとり、頂点B、DからAEにそれぞれ垂線BF、DGをひきます。
また、DFの延長と辺ABとの交点をHとします。
①$AB=AD,BF12cm$、$DG=4cm$のとき、四角形BFDGの面積は?
②$\angle ABF=\angle FDG、\angle AHF=\angle DFG$のとき、
$AG:AE$を、最も簡単な整数の比で表そう。
※図は動画内参照
【受験対策】 数学-関数③

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図で曲線は$y=x^2$のグラフです。
動点Pは原点Oからと軸上を正の方向に毎秒4の速さで移動し、
動点Qは原点OからX軸上を正の方向に毎秒2の速さで移動します。
①動点P、Qが同時に出発して2秒後にできる直線PQの式は?
②①でもとめた直線PQと曲線との2つの交点において、X座標が負の点をR もう一方をSとするとき、2点R、Sの座標は?
③線分RSの長さは?
※図は動画内参照
この動画を見る
右の図で曲線は$y=x^2$のグラフです。
動点Pは原点Oからと軸上を正の方向に毎秒4の速さで移動し、
動点Qは原点OからX軸上を正の方向に毎秒2の速さで移動します。
①動点P、Qが同時に出発して2秒後にできる直線PQの式は?
②①でもとめた直線PQと曲線との2つの交点において、X座標が負の点をR もう一方をSとするとき、2点R、Sの座標は?
③線分RSの長さは?
※図は動画内参照
【はいちのだらだラジオ】 第2回-お礼を言わなきゃ年越しできん

【受験対策】 数学-規則性②
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
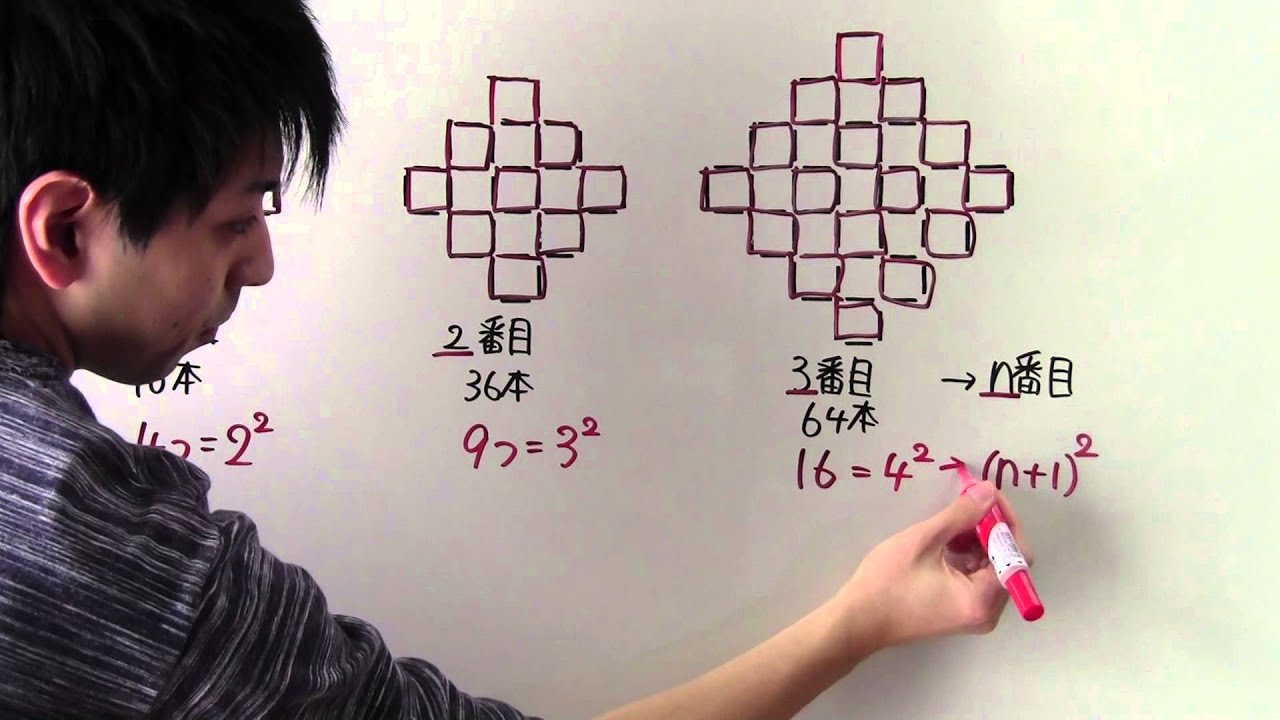
同じ長さのマッチ棒を用いて、下の図のように、一定の規則にしたがって、1番目、2番目3番目、…とマッチ棒をつなぎ合わせて図形をつくっていく。
用いたマッチ棒の数は、1番目では16本、2番目では36本 3番目では64本である。
①4番目の図形をつくるには何本のマッチ棒が必要?
②n番目の図形をつくるには何本のマッチ棒が必要か、nの式で表そう。
※図は動画内参照
この動画を見る
同じ長さのマッチ棒を用いて、下の図のように、一定の規則にしたがって、1番目、2番目3番目、…とマッチ棒をつなぎ合わせて図形をつくっていく。
用いたマッチ棒の数は、1番目では16本、2番目では36本 3番目では64本である。
①4番目の図形をつくるには何本のマッチ棒が必要?
②n番目の図形をつくるには何本のマッチ棒が必要か、nの式で表そう。
※図は動画内参照
【受験対策】 数学-規則性①

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
同じ長さのマッチ棒を用いて、下の図のように、一定の規則にしたがって、1番目、2番目、3番目、…とマッチ棒をつなぎ合わせて図形をつくっていく。
用いたマッチ棒の数は1番目では4本、2番目では12本、 3番目では24本である。
①5番目の図形をつくるには何本のマッチ棒が必要?
②14番目の図形をつくるには何本のマッチ棒が必要?
③n番目の図形をつくるには何本のマッチ棒が必要か、nの式で表そう。
※図は動画内参照
この動画を見る
同じ長さのマッチ棒を用いて、下の図のように、一定の規則にしたがって、1番目、2番目、3番目、…とマッチ棒をつなぎ合わせて図形をつくっていく。
用いたマッチ棒の数は1番目では4本、2番目では12本、 3番目では24本である。
①5番目の図形をつくるには何本のマッチ棒が必要?
②14番目の図形をつくるには何本のマッチ棒が必要?
③n番目の図形をつくるには何本のマッチ棒が必要か、nの式で表そう。
※図は動画内参照
【はいちのだらだラジオ】 第1回-突然どうしちゃったの?

【受験対策】 数学-関数②
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
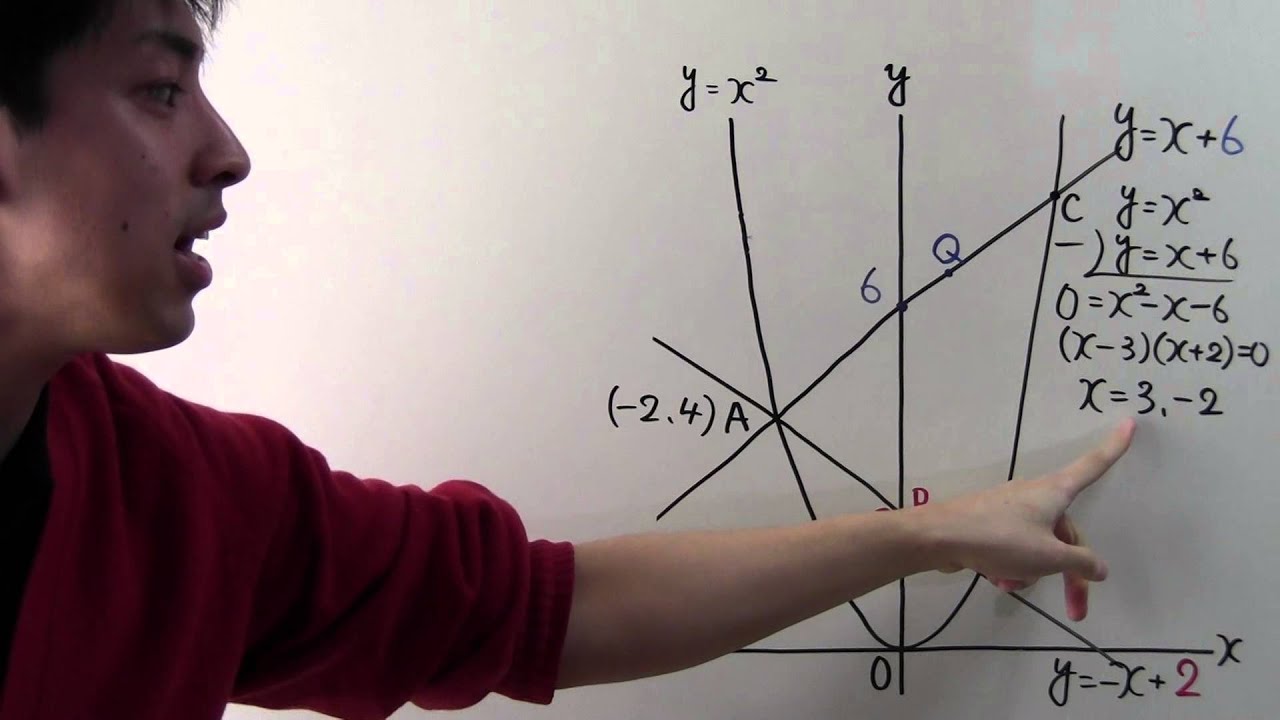
右の図で、曲線は関数$y=x^2$のグラフです。
曲線上の 点A(-2.4)を通り、傾きが-1、1の直線と曲線との交点、をそれぞれB、Cとします。
点P、Qは点Aを同時に出発して、点Pは線分AB上を、点Qは線分AC上を、それぞれ一定の速さで進み、 点Pは点Bに、点Qは点Cに同時に到着しました。
①点Pがy軸上にきたときの点Qの座標は?
②点P、Qが同時に到着した後、点P、Qは線分BC上をそれぞれの速さを変えずに進み、線分BC上の点Rで出会いました。
点Rの座標は?
③△ABRの面積を求めよう。
ただし、座標軸の単位の長さを1cmとします。
※図は動画内参照
この動画を見る
右の図で、曲線は関数$y=x^2$のグラフです。
曲線上の 点A(-2.4)を通り、傾きが-1、1の直線と曲線との交点、をそれぞれB、Cとします。
点P、Qは点Aを同時に出発して、点Pは線分AB上を、点Qは線分AC上を、それぞれ一定の速さで進み、 点Pは点Bに、点Qは点Cに同時に到着しました。
①点Pがy軸上にきたときの点Qの座標は?
②点P、Qが同時に到着した後、点P、Qは線分BC上をそれぞれの速さを変えずに進み、線分BC上の点Rで出会いました。
点Rの座標は?
③△ABRの面積を求めよう。
ただし、座標軸の単位の長さを1cmとします。
※図は動画内参照
【高校受験対策/数学/関数1】交点→面積(王道パターン)

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図で、直線ℓは関数y=3x+9のグラフ、
直線mは関数y=-x+5のグラフです。
また、 y軸と直線ℓ、直線mとの交点をそれぞれA、Bとし、
直線ℓと直線mの交点をPとします。
ただし、座標の 1目もりを1cmとします。
①ABの長さは?
②点Pの座標は?
③△PABの面積は?
④直線上に点Qをとります。
点Qから軸に平行な直線をひき、X軸との交点をRとする。
また、点Qから X軸に平行な直線をひき、直線との交点をSとし、 点Sからy軸に平行な直線をひき、X軸との交点をTとします。
四角形QRTSの周の長さが14cmになるとき、 Qの座標をすべて求めよう!
※図は動画内参照
この動画を見る
右の図で、直線ℓは関数y=3x+9のグラフ、
直線mは関数y=-x+5のグラフです。
また、 y軸と直線ℓ、直線mとの交点をそれぞれA、Bとし、
直線ℓと直線mの交点をPとします。
ただし、座標の 1目もりを1cmとします。
①ABの長さは?
②点Pの座標は?
③△PABの面積は?
④直線上に点Qをとります。
点Qから軸に平行な直線をひき、X軸との交点をRとする。
また、点Qから X軸に平行な直線をひき、直線との交点をSとし、 点Sからy軸に平行な直線をひき、X軸との交点をTとします。
四角形QRTSの周の長さが14cmになるとき、 Qの座標をすべて求めよう!
※図は動画内参照
【小5 算数】 小5-47 割合と百分率② ・ %編

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
表①~⑧の空欄を埋めよう!
◎百分率で表そう!
⑨0.61→
⑩0.03→
⑪0.7→
⑫1.23→
⑬2.8→
⑭1.06→
◎少数で表そう!
⑮189%→
⑯34%→
⑰9%→
⑱60%→
⑲205%→
⑳5.6%→
◎歩合で表そう!
㉑0.321→
㉒1.56→
この動画を見る
表①~⑧の空欄を埋めよう!
◎百分率で表そう!
⑨0.61→
⑩0.03→
⑪0.7→
⑫1.23→
⑬2.8→
⑭1.06→
◎少数で表そう!
⑮189%→
⑯34%→
⑰9%→
⑱60%→
⑲205%→
⑳5.6%→
◎歩合で表そう!
㉑0.321→
㉒1.56→
【小5 算数】 小5-46 割合と百分率① ・ 公式編

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
くらべられる量=④________________
もとにする量 =⑤________________
わりあい =⑥________________
※図は動画内参照
◎5mをもとにするとき、
次の数の割合はいくつ?
⑦8m→
⑧5m→
⑨4m→
⑩2m→
⑪AくんとBくんでは、シュートがよく成功したのはどっち?
※表は動画内参照
この動画を見る
くらべられる量=④________________
もとにする量 =⑤________________
わりあい =⑥________________
※図は動画内参照
◎5mをもとにするとき、
次の数の割合はいくつ?
⑦8m→
⑧5m→
⑨4m→
⑩2m→
⑪AくんとBくんでは、シュートがよく成功したのはどっち?
※表は動画内参照
【数学】中3-72 標本調査②(問題編)

単元:
#数学(中学生)#中3数学#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①人口18000人のA市で、無作為に500人抽出し、「好きなラーメンの味」についてアンケート調査をした。
このとき、A市すべての人のうち、みそ味が好きな人は、およそ何人と推測される?
四捨五入して、百の位までもとめよう。
※表は動画内参照
②袋の中に白玉だけが大量に入っている。
そこに同じ大きさの赤玉30個を入れ、その中から50個を無作為に
抽出する。
これを数回調べると平均6個の赤玉が含まれていた。
袋の中の白玉はおよそ何個と推測される?
この動画を見る
①人口18000人のA市で、無作為に500人抽出し、「好きなラーメンの味」についてアンケート調査をした。
このとき、A市すべての人のうち、みそ味が好きな人は、およそ何人と推測される?
四捨五入して、百の位までもとめよう。
※表は動画内参照
②袋の中に白玉だけが大量に入っている。
そこに同じ大きさの赤玉30個を入れ、その中から50個を無作為に
抽出する。
これを数回調べると平均6個の赤玉が含まれていた。
袋の中の白玉はおよそ何個と推測される?
【数学】中3-71 標本調査①(基本編)

単元:
#数学(中学生)#中3数学#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
ある集団について何かを調べるとき、その集団のすべてについて調べることを①____といい、集団の一部をとり出して調べることを②____という。
②‗‗‗‗‗‗‗‗‗をするとき、何かを調べたい集団全体を③____
といい、とり出した一部の資料を④____という。
④‗‗‗‗‗‗‗‗‗を選ぶときは、⑤_____しなければならない。
◎ある市の中学生全体の勉強時間を調べるために、中学生500人を選んだ。
⑥母集団は?
⑦標本は?
⑧標本の大きさは?
⑨ある中学校で、全校生徒の勉強時間を調べるときに適切ではない標本の集め方はどれ?
$\boxed{ア}$全生徒からくじ引きで25人選ぶ。
$\boxed{イ}$全生徒に通し番号をつけ、乱数さいを使って25人選ぶ。
$\boxed{ウ}$3年2組の中から、無作為に、25人選ぶ。
この動画を見る
ある集団について何かを調べるとき、その集団のすべてについて調べることを①____といい、集団の一部をとり出して調べることを②____という。
②‗‗‗‗‗‗‗‗‗をするとき、何かを調べたい集団全体を③____
といい、とり出した一部の資料を④____という。
④‗‗‗‗‗‗‗‗‗を選ぶときは、⑤_____しなければならない。
◎ある市の中学生全体の勉強時間を調べるために、中学生500人を選んだ。
⑥母集団は?
⑦標本は?
⑧標本の大きさは?
⑨ある中学校で、全校生徒の勉強時間を調べるときに適切ではない標本の集め方はどれ?
$\boxed{ア}$全生徒からくじ引きで25人選ぶ。
$\boxed{イ}$全生徒に通し番号をつけ、乱数さいを使って25人選ぶ。
$\boxed{ウ}$3年2組の中から、無作為に、25人選ぶ。
【小5 算数】 小5-45 高さと面積の関係

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①表を完成させよう!
②高さが2倍、3倍…になると面積はどうなる?
③高さが1cm増えると、面積はどのように変わりますか?
④高さを□$cm$、面積を〇$cm^2$として、平行四辺形の面積を求める式をつくろう。
⑤高さが8.5$cm$のとき、面積は何$cm^2$?
※図は動画内参照
この動画を見る
①表を完成させよう!
②高さが2倍、3倍…になると面積はどうなる?
③高さが1cm増えると、面積はどのように変わりますか?
④高さを□$cm$、面積を〇$cm^2$として、平行四辺形の面積を求める式をつくろう。
⑤高さが8.5$cm$のとき、面積は何$cm^2$?
※図は動画内参照
【小5 算数】 小5-44 ひし形の面積
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
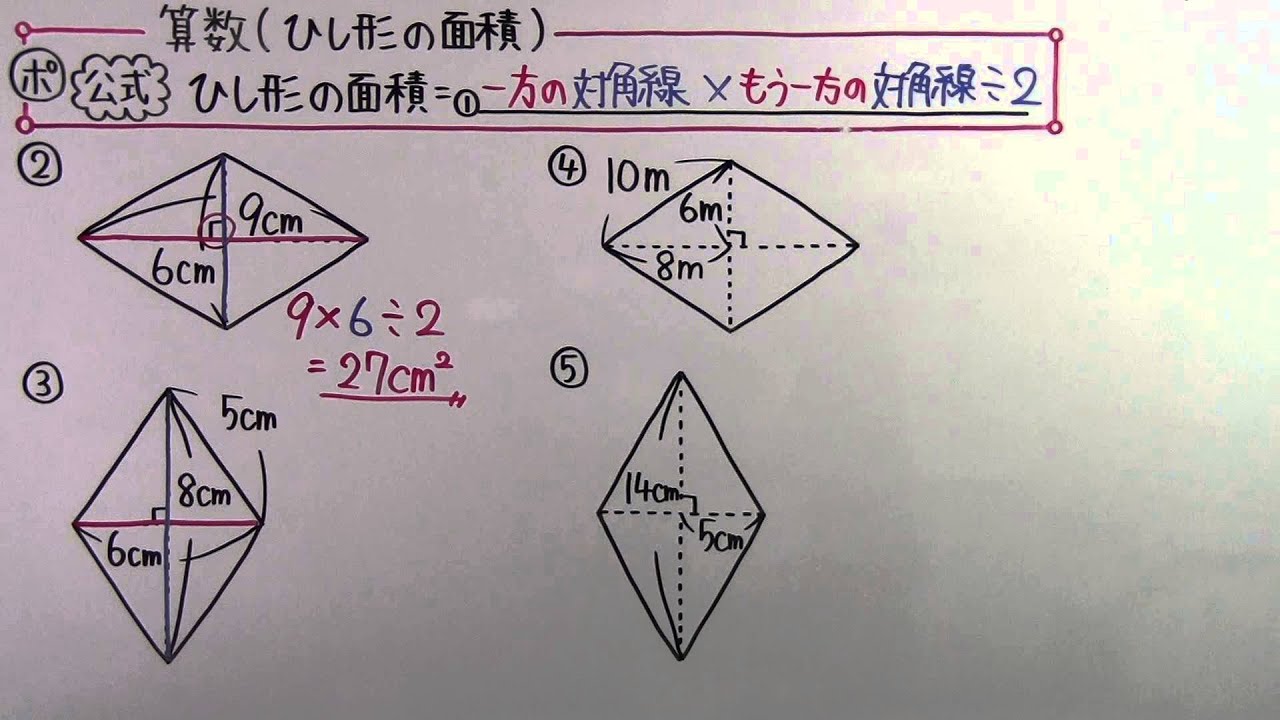
【公式】
ひし形の面積=①_________
②
③
④
⑤
※図は動画内参照
この動画を見る
【公式】
ひし形の面積=①_________
②
③
④
⑤
※図は動画内参照
【小5 算数】 小5-43 台形の面積
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
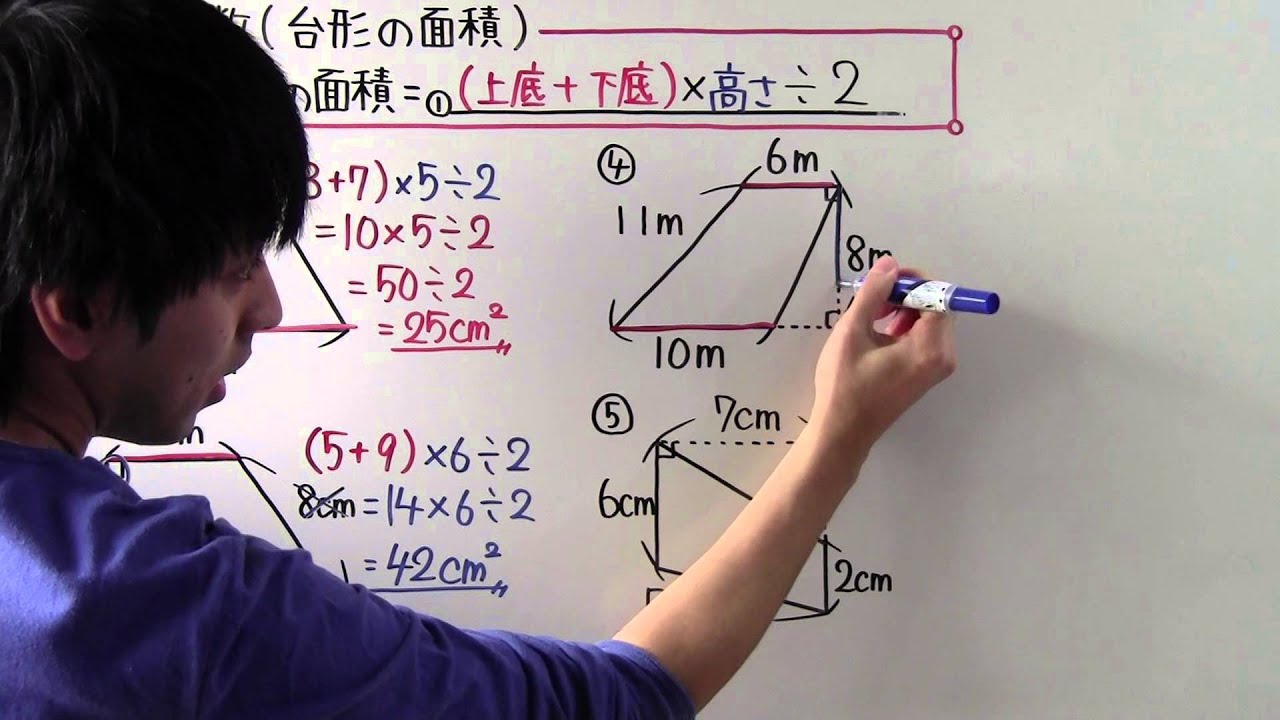
【公式】
台形の面積=①_________
②
③
④
⑤
※図は動画内参照
この動画を見る
【公式】
台形の面積=①_________
②
③
④
⑤
※図は動画内参照
【小5 算数】 小5-42 三角形の面積
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
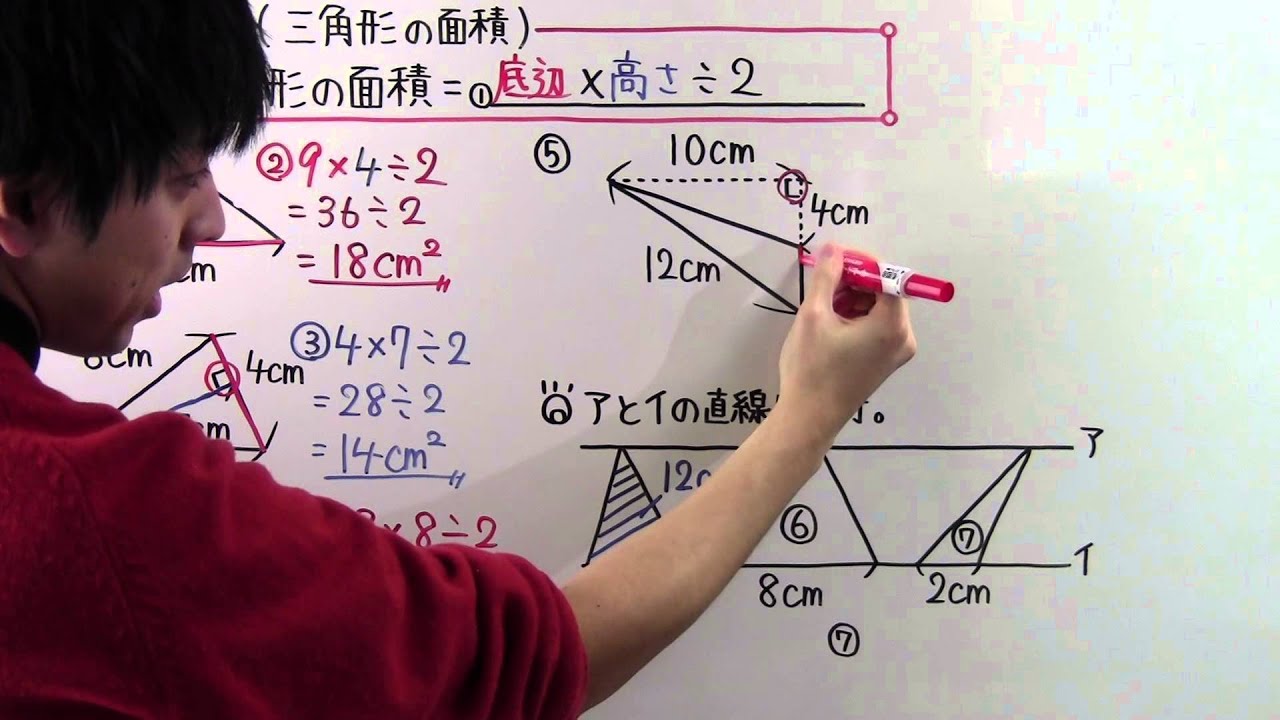
【公式】
三角形の面積=①_________
②
③
④
⑤
◎㋐と㋑の直線は平行。
⑥
⑦
※図は動画内参照
この動画を見る
【公式】
三角形の面積=①_________
②
③
④
⑤
◎㋐と㋑の直線は平行。
⑥
⑦
※図は動画内参照
【小5 算数】 小5-41 平行四辺形の面積

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
【公式】
平行四辺形の面積=①_________
②
③
④
◎㋐と㋑の直線は平行。
⑥
⑦
※図は動画内参照
この動画を見る
【公式】
平行四辺形の面積=①_________
②
③
④
◎㋐と㋑の直線は平行。
⑥
⑦
※図は動画内参照
【英語】中1-39 現在進行形③(疑問詞とのコラボ編)

単元:
#英語(中学生)#中1英語#現在進行形(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①____ ____ ____ ____ now?
あなたは今、何を勉強していますか?
②(返事)__ ____ moth.
③____ ____ ____ ____?
あなたは何をしていますか?
④____ __ __ ____ ____?
彼は今、何をしていますか?
⑤____ ____ ____ ____ ____
彼女たちは何について話していますか?
⑥____ __ ____ ____?
→⑦(返事)__ __ ____ __ ____ ___.
あなたのお父さんはそこで何をしていますか?
⑨____ ____ ____ ____ _____?
だれが私のペンを使っていますか?
この動画を見る
①____ ____ ____ ____ now?
あなたは今、何を勉強していますか?
②(返事)__ ____ moth.
③____ ____ ____ ____?
あなたは何をしていますか?
④____ __ __ ____ ____?
彼は今、何をしていますか?
⑤____ ____ ____ ____ ____
彼女たちは何について話していますか?
⑥____ __ ____ ____?
→⑦(返事)__ __ ____ __ ____ ___.
あなたのお父さんはそこで何をしていますか?
⑨____ ____ ____ ____ _____?
だれが私のペンを使っていますか?
【英語】中1-38 現在進行形②(疑問編)

単元:
#英語(中学生)#中1英語#現在進行形(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①Tom __ ____ the guitar.
トムはギターを弾いています。
②__ ___ ____ the guitar?
トムはギターを弾いていますか?
→③(返事)Yes,__ __. /No,__ __.
④__ ___ ___ ___ __?
マリは今、お茶を飲んでいますか?
→⑤(返事)Yes,__ __. /No,__ __.
⑥__ __ ___ ___ sushi?
彼はまだすしを食べていますか?
→⑦(返事)Yes,__ __. /No,__ __.
⑧____ the boys ____ ___?
男の子はまた走っていますか?
→⑨Yes,__ __. /No,__ __.
この動画を見る
①Tom __ ____ the guitar.
トムはギターを弾いています。
②__ ___ ____ the guitar?
トムはギターを弾いていますか?
→③(返事)Yes,__ __. /No,__ __.
④__ ___ ___ ___ __?
マリは今、お茶を飲んでいますか?
→⑤(返事)Yes,__ __. /No,__ __.
⑥__ __ ___ ___ sushi?
彼はまだすしを食べていますか?
→⑦(返事)Yes,__ __. /No,__ __.
⑧____ the boys ____ ___?
男の子はまた走っていますか?
→⑨Yes,__ __. /No,__ __.
【英語】中1-37 現在進行形①(基本編)

単元:
#英語(中学生)#中1英語#現在進行形(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
進行形の作り方は①_________で、
意味は②____________になるよ!
③I ____ soccer.
私はサッカーをします。
④I __ ____ soccer.
私はサッカーをしています。
⑤__ ____ __.
彼女は今、料理をしています。
⑥He __ ____.
彼は走っているところです。
⑦Syun __ ____ his computer.
シュンはコンピューターを使っています。
⑧__ __ ____ a cake ____.
私たちは一緒にケーキを作っているところです。
⑨Rui __ ____ ____ ____.
ルイは今、英語の勉強をしています。
⑩____ ___ ____ __ school.
彼らはへ歩いているところです。
この動画を見る
進行形の作り方は①_________で、
意味は②____________になるよ!
③I ____ soccer.
私はサッカーをします。
④I __ ____ soccer.
私はサッカーをしています。
⑤__ ____ __.
彼女は今、料理をしています。
⑥He __ ____.
彼は走っているところです。
⑦Syun __ ____ his computer.
シュンはコンピューターを使っています。
⑧__ __ ____ a cake ____.
私たちは一緒にケーキを作っているところです。
⑨Rui __ ____ ____ ____.
ルイは今、英語の勉強をしています。
⑩____ ___ ____ __ school.
彼らはへ歩いているところです。
【英語】中1-36 依頼する・許可をもとめる

単元:
#英語(中学生)#中1英語#canの文(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
Can you~?で①____、
Can I~?で____って意味になるよ!
③___ ___ ___ ____?
買い物に行ってもらえませんか?
④____.
いいですよ。
⑤Yes,__ ____.
はい、もちろん。
⑥____,I'm___ ____.
ごめん、今忙しいんだ。
⑦___ ___ ___ your camera?
あなたのカメラを使ってもいいですか?
⑧____,____ ____.
ごめん、使っちゃダメなんだ。
⑨It's____ ____.
それは私のものじゃないの。
⑩____ ____.
そっか、いいよ。
この動画を見る
Can you~?で①____、
Can I~?で____って意味になるよ!
③___ ___ ___ ____?
買い物に行ってもらえませんか?
④____.
いいですよ。
⑤Yes,__ ____.
はい、もちろん。
⑥____,I'm___ ____.
ごめん、今忙しいんだ。
⑦___ ___ ___ your camera?
あなたのカメラを使ってもいいですか?
⑧____,____ ____.
ごめん、使っちゃダメなんだ。
⑨It's____ ____.
それは私のものじゃないの。
⑩____ ____.
そっか、いいよ。
【英語】中1-35 下線部をたずねる疑問文

単元:
#英語(中学生)#中1英語#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)#He(She) is~. Who is~?の文(肯定文・否定文・疑問文)#代名詞の目的格、所有代名詞、Whose~?と答え方#時刻の表し方とたずね方、曜日・日付のたずね方、When~?、「時」を表す前置詞#Where、Which、Howで始まる疑問文
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎下線部をたずねる疑問文にしよう!
①I play soccer in the park.
※下線部は動画内参照
→_____________________.
②This is a pen.
→_____________________.
③That girl is Mei.
→_____________________.
④He meets her after school.
→_____________________.
⑤I go shopping by bus.
→_____________________.
⑦I have three pens.
→_____________________.
⑧That is her bag.
→_____________________.
この動画を見る
◎下線部をたずねる疑問文にしよう!
①I play soccer in the park.
※下線部は動画内参照
→_____________________.
②This is a pen.
→_____________________.
③That girl is Mei.
→_____________________.
④He meets her after school.
→_____________________.
⑤I go shopping by bus.
→_____________________.
⑦I have three pens.
→_____________________.
⑧That is her bag.
→_____________________.
【英語】中1-34 howの使い方

単元:
#英語(中学生)#中1英語#Where、Which、Howで始まる疑問文
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
howの意味は①____ で、文の②____で使う!
③____ __ __ ____ the guitar?
あなたはどうやってギターをひきますか?
④____ __ __ __ __ my house?
あなたはどうやって私の家に来ますか?
→(返事)__ __.
自転車です。
⑥____ ____ ____ ____ cake?
彼はどうやってケーキを作りますか?
⑦__ __ Yuki __ __?
ユキはどうやってそこに行きますか?
→(返事)__ __.
バスです。
⑨____ __ __ get the card?
私はどうやってそのカードを手に入れることができますか?
⑩____ ____ __ __ __ __?
あなたは何個ボールを持っていますか?
この動画を見る
howの意味は①____ で、文の②____で使う!
③____ __ __ ____ the guitar?
あなたはどうやってギターをひきますか?
④____ __ __ __ __ my house?
あなたはどうやって私の家に来ますか?
→(返事)__ __.
自転車です。
⑥____ ____ ____ ____ cake?
彼はどうやってケーキを作りますか?
⑦__ __ Yuki __ __?
ユキはどうやってそこに行きますか?
→(返事)__ __.
バスです。
⑨____ __ __ get the card?
私はどうやってそのカードを手に入れることができますか?
⑩____ ____ __ __ __ __?
あなたは何個ボールを持っていますか?
【英語】中1-33 canの使い方

単元:
#英語(中学生)#中1英語#canの文(肯定文・否定文・疑問文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
canの意味は①____で、動詞の②____にいれる。
そして、canをいれると動詞は③____になるよ!
④She____ tennis.
彼女はテニスをします。
⑤She __ __ tennis.
彼女はテニスをすることができます。
⑥He ____ ____ English ____ ____.
彼はとても上手に英語を話すことができます。
⑦____ ____ ____ curry?
あなたはカレーを作ることができますか?
→⑧(返事)Yes,__ __./No,__ __.
⑨__ __ __ __.
私たちは早く走ることができません。
⑩____ ____ ____ ____ tennis?
私はどこでテニスをすることができますか?
この動画を見る
canの意味は①____で、動詞の②____にいれる。
そして、canをいれると動詞は③____になるよ!
④She____ tennis.
彼女はテニスをします。
⑤She __ __ tennis.
彼女はテニスをすることができます。
⑥He ____ ____ English ____ ____.
彼はとても上手に英語を話すことができます。
⑦____ ____ ____ curry?
あなたはカレーを作ることができますか?
→⑧(返事)Yes,__ __./No,__ __.
⑨__ __ __ __.
私たちは早く走ることができません。
⑩____ ____ ____ ____ tennis?
私はどこでテニスをすることができますか?
【英語】中2-23 as ~ as 文

単元:
#英語(中学生)#中2英語#比較(比較級、最上級、more,mostを使った比較、as~asの文、不規則変化するもの、疑問詞で始まる比較の文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
『as 形容詞 as Ⓐ』で①____
『not as 形容詞 as Ⓐ』で②____って意味になる!
③Aya is as busy as Emi.
____________
④Aya isn't as busy as Emi.
____________
⑤My bag ___ ___ ____ __ __.
私のバックはあなたのと同じくらいの大きい。
⑥Math __ __ ____ __ ____ ___ ___.
私にとって数学は英語と同じくらい難しい。
My___ ___ ___ ___ ____ my ____.
私の父は母ほど若くない。
⑧This picture ___ ___ ______ ___ ___
______.
この絵はあの絵と同じくらい美しいです。
この動画を見る
『as 形容詞 as Ⓐ』で①____
『not as 形容詞 as Ⓐ』で②____って意味になる!
③Aya is as busy as Emi.
____________
④Aya isn't as busy as Emi.
____________
⑤My bag ___ ___ ____ __ __.
私のバックはあなたのと同じくらいの大きい。
⑥Math __ __ ____ __ ____ ___ ___.
私にとって数学は英語と同じくらい難しい。
My___ ___ ___ ___ ____ my ____.
私の父は母ほど若くない。
⑧This picture ___ ___ ______ ___ ___
______.
この絵はあの絵と同じくらい美しいです。
【英語】中2-22 最上級

単元:
#英語(中学生)#中2英語#比較(比較級、最上級、more,mostを使った比較、as~asの文、不規則変化するもの、疑問詞で始まる比較の文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
最上級の作り方は①____で②____ という意味になる。
そして、もし範囲を書く場合は③____か④____を使おう!
⑤He ____ ____ ____ .
彼は一番上です。
⑥I ____ ____ ____ ____ my family.
私は家族の中で一番背が高いです。
⑦My dog __ __ ____ __ __ ____.
私の犬は4匹の中でもっとも大きいです。
⑧She __ __ __ __ __ __.
彼女は全員の中で一番背が低い生徒です。
⑨__ __ __ __ ____ __ __ Japan?
あなたは日本でもっとも広い湖を知っていますか?
⑩That pen __ __ ____ __ __ ____.
あのペンは3本のなかでもっとも新しいです。
この動画を見る
最上級の作り方は①____で②____ という意味になる。
そして、もし範囲を書く場合は③____か④____を使おう!
⑤He ____ ____ ____ .
彼は一番上です。
⑥I ____ ____ ____ ____ my family.
私は家族の中で一番背が高いです。
⑦My dog __ __ ____ __ __ ____.
私の犬は4匹の中でもっとも大きいです。
⑧She __ __ __ __ __ __.
彼女は全員の中で一番背が低い生徒です。
⑨__ __ __ __ ____ __ __ Japan?
あなたは日本でもっとも広い湖を知っていますか?
⑩That pen __ __ ____ __ __ ____.
あのペンは3本のなかでもっとも新しいです。
【英語】中2-21 比較級

単元:
#英語(中学生)#中2英語#比較(比較級、最上級、more,mostを使った比較、as~asの文、不規則変化するもの、疑問詞で始まる比較の文)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
比較級の作り方は①_______________で、
②______という意味になる!
③My mother ___ ___.
私の母は若いです。
④My mother __ ___ ___ my father.
私の母は父よりも若いです。
⑤Nami ___ ___ ___ Bob.
ナミはボブより忙しいです。
⑥___ ___ ___ ___ ___ ___?
彼のバッグは私のものより新しいですか?
⑦August ___ ___ ___ January ___ ___.
日本は1月より8月の方が暑いです。
⑧___ ___ ___ ___, Japan __ Mexico?
日本とメキシコだと、どちらの国が広いですが?
この動画を見る
比較級の作り方は①_______________で、
②______という意味になる!
③My mother ___ ___.
私の母は若いです。
④My mother __ ___ ___ my father.
私の母は父よりも若いです。
⑤Nami ___ ___ ___ Bob.
ナミはボブより忙しいです。
⑥___ ___ ___ ___ ___ ___?
彼のバッグは私のものより新しいですか?
⑦August ___ ___ ___ January ___ ___.
日本は1月より8月の方が暑いです。
⑧___ ___ ___ ___, Japan __ Mexico?
日本とメキシコだと、どちらの国が広いですが?
【中1 数学】中1-78 おうぎ形の弧と面積④ ~さらにややこしい図形編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎色のついている部分の面積と周の長さをもとめよう!
①
[面]
[周]
②
ACを直径とする半径は、ABを直径とする
半円を点Aを中心に30°回転させたもの。
[面]
[周]
※図は動画内参照
この動画を見る
◎色のついている部分の面積と周の長さをもとめよう!
①
[面]
[周]
②
ACを直径とする半径は、ABを直径とする
半円を点Aを中心に30°回転させたもの。
[面]
[周]
※図は動画内参照
【中1 数学】中1-77 おうぎ形の弧と面積③ ~ややこしい図形編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎色のついている部分の面積と周の長さをもとめよう!
①
[面]
[周]
②
[面]
[周]
※図は動画内参照
この動画を見る
◎色のついている部分の面積と周の長さをもとめよう!
①
[面]
[周]
②
[面]
[周]
※図は動画内参照


