 3rd School
3rd School
 3rd School
3rd School
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【3stepですぐ仕上がる!?】中和の計算方法を解説!〔現役塾講師解説、高校化学、化学基礎〕

単元:
#化学#化学基礎2ー物質の変化#中和と塩#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学基礎
中和の計算方法について解説します。
0.10mol/Lの酢酸水溶液40mLを過不足なく中和するのに0.20mol/Lの水酸化バリウム水溶液を滴下したところ、何mLで中和点に達したか?
0.25 mol/Lの硫酸水溶液50mLを過不足なく中和するのにある濃度の水酸化ナトリウム水溶液を滴下したところ、25mLで中和点に達した。この水酸化ナトリウムの濃度は?
4.0gの水酸化ナトリウムとちょうど中和する硫酸の物質量は?
Na:23、0:16、H:1
この動画を見る
化学基礎
中和の計算方法について解説します。
0.10mol/Lの酢酸水溶液40mLを過不足なく中和するのに0.20mol/Lの水酸化バリウム水溶液を滴下したところ、何mLで中和点に達したか?
0.25 mol/Lの硫酸水溶液50mLを過不足なく中和するのにある濃度の水酸化ナトリウム水溶液を滴下したところ、25mLで中和点に達した。この水酸化ナトリウムの濃度は?
4.0gの水酸化ナトリウムとちょうど中和する硫酸の物質量は?
Na:23、0:16、H:1
【共通テストでも出た!!】電離平衡とpHの計算方法をマスター!〔現役塾講師解説、高校化学、化学基礎〕

単元:
#化学#化学理論#化学平衡と平衡移動#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学
電離平衡とpHの計算方法について解説します。
Q.$25$℃での$0.27$mol/L酢酸水溶液の電離度と水素イオン濃度、pHを求めよ。酢酸の電離定数は$2.7×10^{-5}$mol/Lとする。$\log_{10}2.7=0.43$
この動画を見る
化学
電離平衡とpHの計算方法について解説します。
Q.$25$℃での$0.27$mol/L酢酸水溶液の電離度と水素イオン濃度、pHを求めよ。酢酸の電離定数は$2.7×10^{-5}$mol/Lとする。$\log_{10}2.7=0.43$
【短時間で押さえるべきことをマスター!!】太陽〔現役塾講師解説、中学3年、理科〕

【押さえるべき知識をこの一本でマスター!?】イオン化傾向と電池の基礎〔現役塾講師解説、高校化学、化学基礎〕

【テスト直前でもすぐ仕上がる!?】塩と液性(酸性、中性、塩基性)の判別方法を解説!〔現役塾講師解説、高校化学、化学基礎〕

単元:
#化学#化学基礎2ー物質の変化#中和と塩#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学基礎
塩と液性(酸性、中性、塩基性)の判別方法について解説します。
この動画を見る
化学基礎
塩と液性(酸性、中性、塩基性)の判別方法について解説します。
【問題の解き方をマスター!!】質量モル濃度の求め方を解説!〔現役塾講師解説、高校化学、化学基礎〕

単元:
#化学#化学基礎2ー物質の変化#物質量と濃度#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学
質量モル濃度の求め方について解説します。
Q.硝酸の$\mathsf{1.7mol/L}$水溶液(密度$\mathsf{1.05g/cm^3}$)の質量モル濃度は?
この動画を見る
化学
質量モル濃度の求め方について解説します。
Q.硝酸の$\mathsf{1.7mol/L}$水溶液(密度$\mathsf{1.05g/cm^3}$)の質量モル濃度は?
【演習①】電流と磁界の問題の解き方〔現役塾講師解説、中学2年、理科〕

【理論を理解して問題を解く!!】苦手な人が多い緩衝液を解説!〔現役塾講師解説、高校化学、化学基礎〕

【この一本でpH計算はバッチリ!?】pH、電離度の計算の方法を解説!〔現役塾講師解説、高校化学、化学基礎〕

単元:
#化学#化学基礎2ー物質の変化#酸と塩基・水素イオン濃度#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学基礎
pH、電離度の計算の方法について解説します。
この動画を見る
化学基礎
pH、電離度の計算の方法について解説します。
【月の形をマスター!!】月の満ち欠け、日食、月食〔現役塾講師解説、中学3年、理科〕

【水素イオン濃度ってどう求める!?】電離度と水素イオン濃度の知識を確認して計算をできるようにしよう!〔現役塾講師解説、高校化学、化学基礎〕

【共通テスト化学解答解説】現役塾講師による詳しい解説と講評 !〔現役塾講師解説、高校化学、化学基礎〕

【最速!共通テスト化学基礎解答解説】現役塾講師による詳しい解説と講評 !〔現役塾講師解説、高校化学、化学基礎〕

【分数の式は使いません!!】苦手な人が多い固体の溶解度の計算方法を解説!〔現役塾講師解説、高校化学、化学基礎〕

【式の作り方と計算をこの一本でマスター!?】半反応式の作り方と酸化還元滴定〔現役塾講師解説、高校化学、化学基礎〕

単元:
#化学#化学基礎2ー物質の変化#酸化還元反応#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学基礎
半反応式の作り方と酸化還元滴定について解説します。
この動画を見る
化学基礎
半反応式の作り方と酸化還元滴定について解説します。
【押さえる事項をチェック!】新要領の放射線まとめ〔現役塾講師解説、中学2年、理科〕

【どっちが酸!?塩基!?】ブレンステッドの酸・塩基の決定〔現役塾講師解説、高校化学、化学基礎〕

単元:
#化学#化学基礎2ー物質の変化#酸と塩基・水素イオン濃度#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学基礎
ブレンステッドの酸・塩基の決定について解説します。
この動画を見る
化学基礎
ブレンステッドの酸・塩基の決定について解説します。
【共通テスト最頻出の1つ!!】モル濃度と質量パーセント濃度の変化の問題を短時間で解こう!〔現役塾講師解説、高校化学、化学基礎〕

単元:
#化学#化学基礎2ー物質の変化#物質量と濃度#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学基礎・化学
モル濃度と質量パーセント濃度の変化の問題について解説します。
Q.ブドウ糖(グルコース、分子量$180$) の質量パーセント濃度$5.0\mathsf{%}$水溶液は点滴に用いられている。この水溶液のモル濃度は何$\mathsf{mol/L}$か。ただし、この水溶液の密度は$1.0\mathsf{g/cm^3}$とする。
この動画を見る
化学基礎・化学
モル濃度と質量パーセント濃度の変化の問題について解説します。
Q.ブドウ糖(グルコース、分子量$180$) の質量パーセント濃度$5.0\mathsf{%}$水溶液は点滴に用いられている。この水溶液のモル濃度は何$\mathsf{mol/L}$か。ただし、この水溶液の密度は$1.0\mathsf{g/cm^3}$とする。
【ポイントは何性か!?】有機化合物の分離の基礎事項をおさらい!〔現役塾講師解説、高校化学〕

【共通テストなどのマーク式でよく出る!!】凝固点降下・沸点上昇〜沸点と凝固点の大きさ比べの問題〜〔現役塾講師解説、高校化学、化学基礎〕

単元:
#化学#化学理論#溶液の性質#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学
凝固点降下・沸点上昇について解説します。
A. グルコース(分子量180)4.5gを0.500kgの水に溶かした溶媒
B. 尿素(分子量60.0)4.5gを0.500kgの水に溶かした溶媒
C. 塩化カリウム(分子量74.6)4.5gを0.500kgの水に溶かした溶媒
(1)沸点の高い順に並べよ。水の沸点上昇は0.52K・kg/molとする。
(2)凝固点の高い順に並べよ。水の沸点上昇は1.85K・kg/molとする。
この動画を見る
化学
凝固点降下・沸点上昇について解説します。
A. グルコース(分子量180)4.5gを0.500kgの水に溶かした溶媒
B. 尿素(分子量60.0)4.5gを0.500kgの水に溶かした溶媒
C. 塩化カリウム(分子量74.6)4.5gを0.500kgの水に溶かした溶媒
(1)沸点の高い順に並べよ。水の沸点上昇は0.52K・kg/molとする。
(2)凝固点の高い順に並べよ。水の沸点上昇は1.85K・kg/molとする。
【どのグラフか選ぶ!?】化学反応式と量的関係計算(モル計算)〜グラフを選ぶ問題の解き方を短時間でマスター!!〜〔現役塾講師解説、高校化学、化学基礎〕

単元:
#化学#化学基礎2ー物質の変化#化学変化と化学反応式#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学基礎
化学反応式と量的関係計算(モル計算)について解説します。
この動画を見る
化学基礎
化学反応式と量的関係計算(モル計算)について解説します。
【出るポイントを短時間でチェック!】芳香族アミン(アニリン、ジアゾ化、カップリング)の基礎事項をおさらい!〔現役塾講師解説、高校化学〕

単元:
#化学#有機#芳香族化合物#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学
芳香族アミンについて解説します。
アニリン、アニリン塩酸塩、ジアゾ化、カップリング
この動画を見る
化学
芳香族アミンについて解説します。
アニリン、アニリン塩酸塩、ジアゾ化、カップリング
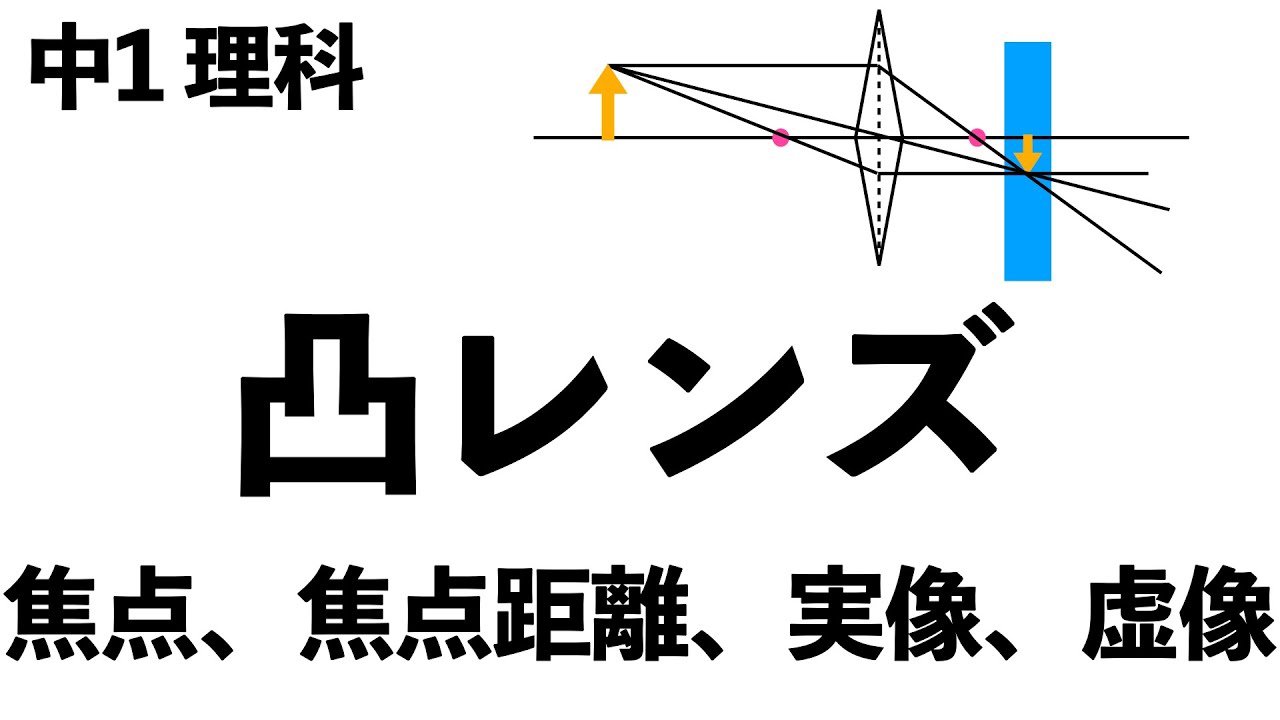
【押さえるべき用語は何!?】凸レンズ〔現役塾講師解説、中学1年、理科〕
【素早く計算方法を学ぶ!!】テスト直前の人向けのヘンリーの法則の計算演習〔現役塾講師解説、高校化学、化学基礎〕

【ちょっと量が多いと思ったらこれ!】過不足ある量的関係計算(モル計算)を短時間でマスター!!〔現役塾講師解説、高校化学、化学基礎〕

単元:
#化学#化学基礎2ー物質の変化#化学変化と化学反応式#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学基礎
量的関係計算(モル計算)について解説します。
プロパン3.0Lと酸素20Lを混合して完全燃焼させると、反応後の混合気体は何Lになるか?ただし、生じた水は全て液体とする。
気体のエチレン1.4gに、標準状態で5.6Lの酸素を混合して点火すると一方の気体の一部が未反応のまま残った。未反応のまま残った気体の質量は?
この動画を見る
化学基礎
量的関係計算(モル計算)について解説します。
プロパン3.0Lと酸素20Lを混合して完全燃焼させると、反応後の混合気体は何Lになるか?ただし、生じた水は全て液体とする。
気体のエチレン1.4gに、標準状態で5.6Lの酸素を混合して点火すると一方の気体の一部が未反応のまま残った。未反応のまま残った気体の質量は?
【出るポイントを短時間でチェック!】芳香族カルボン酸(安息香酸、フタル酸、サリチル酸)の基礎事項をおさらい!〔現役塾講師解説、高校化学〕

【ポイントを素早くチェック!!】太陽系〔現役塾講師解説、中学3年、理科〕

単元:
#理科(中学生)#地学
指導講師:
3rd School
問題文全文(内容文):
中学3年生 理科
太陽系について解説します。
惑星、衛星、恒星、小惑星、すい星、太陽系外縁天体、流星、銀河、銀河系
この動画を見る
中学3年生 理科
太陽系について解説します。
惑星、衛星、恒星、小惑星、すい星、太陽系外縁天体、流星、銀河、銀河系
【不等式はこれを抑えよう!】不等式の証明での注意点をすべてまとめました!〔数学 高校数学〕

【流れを押さえて得意になる!!】苦手な人が多いルシャトリエの原理の問題を全パターン解説!〔現役塾講師解説、高校化学、化学基礎〕

【複雑な化学反応式にはこの方法を!】未定係数法の解き方を短時間でマスター!!〔現役塾講師解説、高校化学、化学基礎〕


