 ぺんぎん高校化学問題集
ぺんぎん高校化学問題集
 ぺんぎん高校化学問題集
ぺんぎん高校化学問題集
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
有機化学第31回 サリチル酸(+アセチルサリチル酸,サリチル酸メチル)

単元:
#化学#有機#芳香族化合物#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
有機化学第31回 サリチル酸(+アセチルサリチル酸,サリチル酸メチル)
サリチル酸
→メタノール
・$FeCl_3$水溶液
・$NaHCO_3$水溶液
この動画を見る
有機化学第31回 サリチル酸(+アセチルサリチル酸,サリチル酸メチル)
サリチル酸
→メタノール
・$FeCl_3$水溶液
・$NaHCO_3$水溶液
共通テスト(旧センター試験)過去問解説 化学 2016年追試 第4問 問1 エタノールの性質

単元:
#化学#有機#大学入試過去問(化学)#酸素を含む脂肪族化合物#共通テスト#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
エタノールに関する記述として誤りを含むものを、次の①~⑥のうちから一 つ選べ。
① 糖類の発酵によって得ることができる。
② 水と任意の割合で溶け合う。
③ ナトリウムと反応させると、水素が発生する。
④ 硫酸酸性のニクロム酸カリウムで酸化すると、
アセトアルデヒドが生成する。
⑤ ヨウ素および水酸化ナトリウム水溶液を加えて加熱すると、黄色沈殿が生成する。
⑥ フェーリング液を加えて加熱すると、赤色の酸化銅(I)が析出する。
この動画を見る
エタノールに関する記述として誤りを含むものを、次の①~⑥のうちから一 つ選べ。
① 糖類の発酵によって得ることができる。
② 水と任意の割合で溶け合う。
③ ナトリウムと反応させると、水素が発生する。
④ 硫酸酸性のニクロム酸カリウムで酸化すると、
アセトアルデヒドが生成する。
⑤ ヨウ素および水酸化ナトリウム水溶液を加えて加熱すると、黄色沈殿が生成する。
⑥ フェーリング液を加えて加熱すると、赤色の酸化銅(I)が析出する。
【聖マリアンナ医科大学】令和5年度一般選抜試験(前期) 天然高分子化合物 過去問解説!(後半)

単元:
#化学#大学入試過去問(化学)#化学(高分子)#合成繊維と天然繊維#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
等電点をもつ分子はどれか。
ア)$H_2N(CH_2)_2COOH$
イ)$C_6H_5NH_2$
ウ)$HSCH_2CH(NH_2)COOH$
エ)$CH_3SCH_2CH_2CH(NH_2)COOH$
オ)$C_6H_5CH_2CH(NH_2)COOH$
カ)$CH_3CH(OH)COOH$
キ)$(C_{17}H_{33}COO)_3C_3H_5$
ニンヒドリン反応をする分子はどれか。
ア)$H_2N(CH_2)_2COOH$
イ)$C_6H_5NH_2$
ウ)$HSCH_2CH(NH_2)COOH$
エ)$CH_3SCH_2CH_2CH(NH_2)COOH$
オ)$C_6H_5CH_2CH(NH_2)COOH$
カ)$CH_3CH(OH)COOH$
キ)$(C_{17}H_{33}COO)_3C_3H_5$
タンパク質の一次構造を15字以内で説明せよ。
解答例:ペプチドのアミノ酸配列
タンパク質の二次構造に見られず、三次構造で見られる共有 結合の名称と、この結合をする分子を2つ選べ。同じものを2回選んでもよい。
ア)$H_2N(CH_2)_2COOH$
イ)$C_6H_5NH_2$
ウ)$HSCH_2CH(NH_2)COOH$
エ)$CH_3SCH_2CH_2CH(NH_2)COOH$
オ)$C_6H_5CH_2CH(NH_2)COOH$
カ)$CH_3CH(OH)COOH$
キ)$(C_{17}H_{33}COO)_3C_3H_5$
油脂を選べ。
また、この油脂のけん化価(油脂$1g$を完全に加水分解するために必要な$KOH$の質量[mg])を有効数字2桁で求めなさい。
(原子量 $H 1 C 12 O 16 K 39$)
この油脂$1mol$の$C=C$すべてに水素を付加させるとき、何$mol$ の水素が必要か自然数で求めよ。
この動画を見る
等電点をもつ分子はどれか。
ア)$H_2N(CH_2)_2COOH$
イ)$C_6H_5NH_2$
ウ)$HSCH_2CH(NH_2)COOH$
エ)$CH_3SCH_2CH_2CH(NH_2)COOH$
オ)$C_6H_5CH_2CH(NH_2)COOH$
カ)$CH_3CH(OH)COOH$
キ)$(C_{17}H_{33}COO)_3C_3H_5$
ニンヒドリン反応をする分子はどれか。
ア)$H_2N(CH_2)_2COOH$
イ)$C_6H_5NH_2$
ウ)$HSCH_2CH(NH_2)COOH$
エ)$CH_3SCH_2CH_2CH(NH_2)COOH$
オ)$C_6H_5CH_2CH(NH_2)COOH$
カ)$CH_3CH(OH)COOH$
キ)$(C_{17}H_{33}COO)_3C_3H_5$
タンパク質の一次構造を15字以内で説明せよ。
解答例:ペプチドのアミノ酸配列
タンパク質の二次構造に見られず、三次構造で見られる共有 結合の名称と、この結合をする分子を2つ選べ。同じものを2回選んでもよい。
ア)$H_2N(CH_2)_2COOH$
イ)$C_6H_5NH_2$
ウ)$HSCH_2CH(NH_2)COOH$
エ)$CH_3SCH_2CH_2CH(NH_2)COOH$
オ)$C_6H_5CH_2CH(NH_2)COOH$
カ)$CH_3CH(OH)COOH$
キ)$(C_{17}H_{33}COO)_3C_3H_5$
油脂を選べ。
また、この油脂のけん化価(油脂$1g$を完全に加水分解するために必要な$KOH$の質量[mg])を有効数字2桁で求めなさい。
(原子量 $H 1 C 12 O 16 K 39$)
この油脂$1mol$の$C=C$すべてに水素を付加させるとき、何$mol$ の水素が必要か自然数で求めよ。
共通テスト(旧センター試験)過去問解説 化学 2016年追試 第3問 問6 銅と熱濃硫酸の反応
単元:
#化学#化学基礎2ー物質の変化#大学入試過去問(化学)#共通テスト#酸化還元反応#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
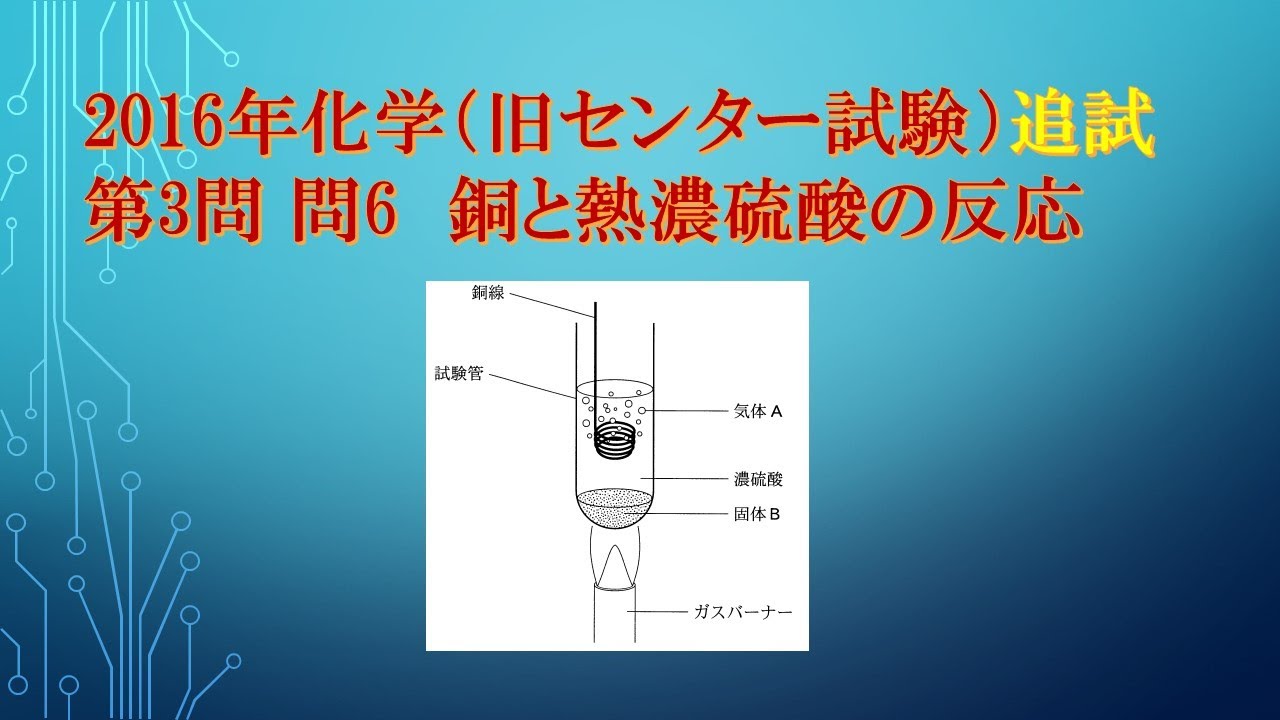
図1に示すように、試験管に濃硫酸を入れて加熱しながら、そこに銅線を注意深く浸したところ、刺激臭のある気体$A$が発生した。
濃硫酸は徐々に着色し、しばらくすると試験管の底に白色の固体$B$が沈殿した。
固体$B$を取り出し水に溶かすと、その溶液は青色となった。
この実験で発生した気体と生成した固体$B$に関する記述として誤りを含むものを、下の①~⑤のうちから一つ選べ。
① 気体$A$は、下方置換で捕集できる。
② 硫化水素の水溶液に気体$A$を通じると、硫黄が析出する。
③ ヨウ素を溶かしたヨウ化カリウム水溶液に気体$A$を通じると、ヨウ素の色が消える。
④ 気体$A$を水に溶かした水溶液は、中性を示す。
⑤ 固体$$Bは、硫酸銅(II)の無水物(無水塩)である。
※図は動画内参照
この動画を見る
図1に示すように、試験管に濃硫酸を入れて加熱しながら、そこに銅線を注意深く浸したところ、刺激臭のある気体$A$が発生した。
濃硫酸は徐々に着色し、しばらくすると試験管の底に白色の固体$B$が沈殿した。
固体$B$を取り出し水に溶かすと、その溶液は青色となった。
この実験で発生した気体と生成した固体$B$に関する記述として誤りを含むものを、下の①~⑤のうちから一つ選べ。
① 気体$A$は、下方置換で捕集できる。
② 硫化水素の水溶液に気体$A$を通じると、硫黄が析出する。
③ ヨウ素を溶かしたヨウ化カリウム水溶液に気体$A$を通じると、ヨウ素の色が消える。
④ 気体$A$を水に溶かした水溶液は、中性を示す。
⑤ 固体$$Bは、硫酸銅(II)の無水物(無水塩)である。
※図は動画内参照
1分で解いてほしい化学計算問題 (32) 緩衝液のpH

単元:
#化学#化学基礎2ー物質の変化#酸と塩基・水素イオン濃度#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
[2021年 愛知学院大学・改]
$0.030mol/L$の酢酸水溶液$100mL$と$0.030mol/L$の酢酸ナトリウム水溶液$100mL$を
混合した溶液の$pH$を小数第1位までの値で求めなさい。
酢酸の電離定数 $Ka = \times 10^{-5}, log_{10}3 = 0.47$とする。
この動画を見る
[2021年 愛知学院大学・改]
$0.030mol/L$の酢酸水溶液$100mL$と$0.030mol/L$の酢酸ナトリウム水溶液$100mL$を
混合した溶液の$pH$を小数第1位までの値で求めなさい。
酢酸の電離定数 $Ka = \times 10^{-5}, log_{10}3 = 0.47$とする。
【聖マリアンナ医科大学】令和5年度一般選抜試験(前期) 天然高分子化合物 過去問解説!(前半)

単元:
#化学#大学入試過去問(化学)#化学(高分子)#アミノ酸とタンパク質、核酸#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
[1]1) 問題概要
①・②の官能基の名称を答え、構造式を書きなさい。
③の構造の名称を答え、構造式を書きなさい。
(価標省略不可)
[1]2) 問題概要 $H 1.00 C 12.0 N 14.0 Ο 16.0$
グリシルアラニンの分子量を自然数で求めよ。
ただし、電離 はしていないものとする
[1]2) 問題概要
アラニン1分子と2分子からなるトリペプチドは 鏡像異性体を含めて何種類異性体があるか。
[1]3) 問題概要
アラニン1分子と2分子からなるトリペプチドは 鏡像異性体を含めて何種類異性体があるか。
$H_2N- \boxed{ Gly } \boxed{ Gly } \boxed{ Ala } - COOH$
並べ方はアラニンをどこに置くかで3通り
更にアラニンは鏡像異性体をもつため2種類ある
3× 2 = 6種類
※構造式は動画内参照
この動画を見る
[1]1) 問題概要
①・②の官能基の名称を答え、構造式を書きなさい。
③の構造の名称を答え、構造式を書きなさい。
(価標省略不可)
[1]2) 問題概要 $H 1.00 C 12.0 N 14.0 Ο 16.0$
グリシルアラニンの分子量を自然数で求めよ。
ただし、電離 はしていないものとする
[1]2) 問題概要
アラニン1分子と2分子からなるトリペプチドは 鏡像異性体を含めて何種類異性体があるか。
[1]3) 問題概要
アラニン1分子と2分子からなるトリペプチドは 鏡像異性体を含めて何種類異性体があるか。
$H_2N- \boxed{ Gly } \boxed{ Gly } \boxed{ Ala } - COOH$
並べ方はアラニンをどこに置くかで3通り
更にアラニンは鏡像異性体をもつため2種類ある
3× 2 = 6種類
※構造式は動画内参照
無機化学第27回 系統分析

有機化学第30回 芳香族カルボン酸(安息香酸・フタル酸・テレフタル酸)

単元:
#化学#有機#芳香族化合物#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
有機化学第30回 芳香族カルボン酸(安息香酸・フタル酸・テレフタル酸)
安息香酸
フタル酸
テレフタル酸
(イソフタル酸)
この動画を見る
有機化学第30回 芳香族カルボン酸(安息香酸・フタル酸・テレフタル酸)
安息香酸
フタル酸
テレフタル酸
(イソフタル酸)
1分で解いてほしい化学計算問題 (31) ダニエル電池

単元:
#化学#化学理論#電池と電気分解#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
〔2023年 神奈川大学・改〕
$ZnSO_4$の水溶液に亜鉛板を浸したものと、$Cu^{2+}$を含む水溶液に銅板を浸したものを、
素焼き板(セパレーター)で隔てて組み合わせることでダニエル電池を作製した。
この電池を放電したところ、$1.93 \times 10^3C$の電気量が流れた。
放電により析出した金属は何$g$か。
有効数字2桁で答えなさい。
ファラデー定数:$9.65 \times 10^4C/mol Cu 63.5 Zn 65.4$
この動画を見る
〔2023年 神奈川大学・改〕
$ZnSO_4$の水溶液に亜鉛板を浸したものと、$Cu^{2+}$を含む水溶液に銅板を浸したものを、
素焼き板(セパレーター)で隔てて組み合わせることでダニエル電池を作製した。
この電池を放電したところ、$1.93 \times 10^3C$の電気量が流れた。
放電により析出した金属は何$g$か。
有効数字2桁で答えなさい。
ファラデー定数:$9.65 \times 10^4C/mol Cu 63.5 Zn 65.4$
共通テスト(旧センター試験)過去問解説 化学 2016年追試 第3問 問5 硫酸鉄(Ⅲ)のモル濃度

単元:
#化学#化学基礎2ー物質の変化#大学入試過去問(化学)#物質量と濃度#共通テスト#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
濃度不明の硫酸鉄(Ⅲ) $Fe_2(SO_4)_3$、水溶液の濃度を求めるために、次の実験Ⅰおよび実験Ⅱを行った。
ただし、この溶液には硫酸鉄(Ⅲ)のみが溶質として含まれているとする。
実験Ⅰ この溶液$20ml$ をピーカーに採取し、濃アンモニア水を徐々に加えると沈殿が生成した。
さらに濃アンモニア水を加え、新たに沈殿が生じないことを確認した。
実験Ⅱ 実験Ⅰで生成した沈殿をすべて回収し、十分洗浄した後、耐熱性の容器に入れて空気中で$600℃$までゆっくり加熱した。
最終的に$160mg$の純粋な酸化鉄(Ⅲ)が得られた。
もとの溶液中の硫酸鉄(Ⅲ)の濃度は何$mol/L$か。
最も適当な数値を、次の①~⑥のうちから一つ選べ。
①$0.0050$
②$0.010$
③$0.020$
④$0.050$
⑤$0.10$
⑥$0.20$
この動画を見る
濃度不明の硫酸鉄(Ⅲ) $Fe_2(SO_4)_3$、水溶液の濃度を求めるために、次の実験Ⅰおよび実験Ⅱを行った。
ただし、この溶液には硫酸鉄(Ⅲ)のみが溶質として含まれているとする。
実験Ⅰ この溶液$20ml$ をピーカーに採取し、濃アンモニア水を徐々に加えると沈殿が生成した。
さらに濃アンモニア水を加え、新たに沈殿が生じないことを確認した。
実験Ⅱ 実験Ⅰで生成した沈殿をすべて回収し、十分洗浄した後、耐熱性の容器に入れて空気中で$600℃$までゆっくり加熱した。
最終的に$160mg$の純粋な酸化鉄(Ⅲ)が得られた。
もとの溶液中の硫酸鉄(Ⅲ)の濃度は何$mol/L$か。
最も適当な数値を、次の①~⑥のうちから一つ選べ。
①$0.0050$
②$0.010$
③$0.020$
④$0.050$
⑤$0.10$
⑥$0.20$
共通テスト(旧センター試験)過去問解説 化学 2016年追試 第3問 問4 金属イオンの反応

単元:
#化学#無機#大学入試過去問(化学)#共通テスト#典型金属元素の単体と化合物#遷移元素の単体と化合物#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
次のアおよびイの3種類のイオンを含む各水溶液から、下線を引いたイオンのみを沈殿として分離したい。
最も適当な方法を、下の①~④のうちから一つずつ選べ。
ただし、同じものを選んでもよい。
ア $Pb^{2+},Fe^{2+}, Ca^{2+}$
イ $Cu^{2+},Pb^{2+},Al^{3+}$
① 水酸化ナトリウム水溶液を過剰に加える。
②アンモニア水を過剰に加える。
③ 室温で希塩酸を加える。
④ アンモニア水を加えて塩基性にしたのち、硫化水素を通じる。
この動画を見る
次のアおよびイの3種類のイオンを含む各水溶液から、下線を引いたイオンのみを沈殿として分離したい。
最も適当な方法を、下の①~④のうちから一つずつ選べ。
ただし、同じものを選んでもよい。
ア $Pb^{2+},Fe^{2+}, Ca^{2+}$
イ $Cu^{2+},Pb^{2+},Al^{3+}$
① 水酸化ナトリウム水溶液を過剰に加える。
②アンモニア水を過剰に加える。
③ 室温で希塩酸を加える。
④ アンモニア水を加えて塩基性にしたのち、硫化水素を通じる。
1分で解いてほしい化学計算問題 (30) エタノールとジエチルエーテル

単元:
#化学#有機#酸素を含む脂肪族化合物#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
〔2021年 愛知工業大学・改〕
エタノール(分子量$46$) とジエチルエーテル(分子量$74$)からなる混 合物がある。
この混合物$115g$に十分な量のナトリウムを加えたところ、水素が$0.200mol$発生した。
混合物中のエタノールの含有率は質量パーセントで何$%$か。
答えは整数で答えよ。
この動画を見る
〔2021年 愛知工業大学・改〕
エタノール(分子量$46$) とジエチルエーテル(分子量$74$)からなる混 合物がある。
この混合物$115g$に十分な量のナトリウムを加えたところ、水素が$0.200mol$発生した。
混合物中のエタノールの含有率は質量パーセントで何$%$か。
答えは整数で答えよ。
【星薬科大学】2023年度化学 一般選抜B方式 天然高分子化合物 過去問解説!

単元:
#化学#大学入試過去問(化学)#化学(高分子)#合成繊維と天然繊維#理科(高校生)#星薬科大学
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
分子量$828$の$8.28g$を加水分解して得たグルコース全量から$400mL$のグルコース水溶液を調製すると、そのモル濃度は何$mol/L$になるか。
ポリ乳酸が該当するものとして、最も適当なものを選べ。
1.レーヨン
2.アクリル繊維
3.ユリア樹脂
4.ビニロン
5.ポリスチレン
6.ポリエステル
7.ポリアミド
8.アセテート
ア:分子量$7434$のポリ乳酸$100g$が微生物に分解されて生じ た二酸化炭素の体積〔L〕を求めよ。
イ:その二酸化炭素がすべて光合成によってグルコースに変
換された場合の質量 〔g〕を求めよ。
この動画を見る
分子量$828$の$8.28g$を加水分解して得たグルコース全量から$400mL$のグルコース水溶液を調製すると、そのモル濃度は何$mol/L$になるか。
ポリ乳酸が該当するものとして、最も適当なものを選べ。
1.レーヨン
2.アクリル繊維
3.ユリア樹脂
4.ビニロン
5.ポリスチレン
6.ポリエステル
7.ポリアミド
8.アセテート
ア:分子量$7434$のポリ乳酸$100g$が微生物に分解されて生じ た二酸化炭素の体積〔L〕を求めよ。
イ:その二酸化炭素がすべて光合成によってグルコースに変
換された場合の質量 〔g〕を求めよ。
無機化学第26回 金属イオンの反応

有機化学第29回 クメン法(フェノールの工業的製法)

共通テスト(旧センター試験)過去問解説 化学 2016年追試 第3問 問3 金属の性質と利用

単元:
#化学#無機#大学入試過去問(化学)#共通テスト#典型金属元素の単体と化合物#遷移元素の単体と化合物#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
金属元素に関する記述として下線部に誤りを含むものを、
次の①~⑤のうちから一つ選べ。
①アルミニウムの単体は$AI^{3+}$を含む水溶液の電気分解により得られる。
② $AgCl$や $AgBr$ に光が当たると分解し $Ag$が析出する現象は、写真のフィ ルムなどに利用される。
③ 白金やニッケルは、触媒として利用されている。
④ 鉛は、放射線の遮蔽材として利用されている。
⑤ マグネシウムの単体は、空気中で強熱すると明るい光を発して燃焼し、酸化マグネシウムを生じる。
この動画を見る
金属元素に関する記述として下線部に誤りを含むものを、
次の①~⑤のうちから一つ選べ。
①アルミニウムの単体は$AI^{3+}$を含む水溶液の電気分解により得られる。
② $AgCl$や $AgBr$ に光が当たると分解し $Ag$が析出する現象は、写真のフィ ルムなどに利用される。
③ 白金やニッケルは、触媒として利用されている。
④ 鉛は、放射線の遮蔽材として利用されている。
⑤ マグネシウムの単体は、空気中で強熱すると明るい光を発して燃焼し、酸化マグネシウムを生じる。
1分で解いてほしい化学計算問題 (29) 量的関係の基本

単元:
#化学#化学理論#気体の性質#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
[2023年 北里大学(薬)・改]
ある元素Aの単体(固体)$1.6g$を容積の変わらない反応容器に酸素とともに密閉し、完全燃焼させた後、もとの温度に戻したところ、容器の圧力は反応前と同じ値になった。
このとき発生した酸化物は$3.2g$であった。
この元素$A$の原子量を有効数字2桁で求めよ。
ただし、固体の体積は気体の体積に比べて無視できるものとす
る。(原子量$O = 16$)
この動画を見る
[2023年 北里大学(薬)・改]
ある元素Aの単体(固体)$1.6g$を容積の変わらない反応容器に酸素とともに密閉し、完全燃焼させた後、もとの温度に戻したところ、容器の圧力は反応前と同じ値になった。
このとき発生した酸化物は$3.2g$であった。
この元素$A$の原子量を有効数字2桁で求めよ。
ただし、固体の体積は気体の体積に比べて無視できるものとす
る。(原子量$O = 16$)
2016年共通テスト(旧センター試験)追試第3問 問2 第4周期の遷移元素に関する問題

単元:
#化学#無機#遷移元素の単体と化合物#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
第4周期の遷移元素に関する記述として誤りを含むものを、次の①~⑤のうちから一つ選べ。
① ほかのイオンや分子と結合した錯イオンを形成するものが多い。
② イオンや化合物は、有色のものが多い。
③ 原子の最外殻電子の数は、族の番号に一致する。
④ 融点が高く、密度が大きい単体が多い。
⑤ 酸化数+6以上の原子を含む化合物が存在する。
この動画を見る
第4周期の遷移元素に関する記述として誤りを含むものを、次の①~⑤のうちから一つ選べ。
① ほかのイオンや分子と結合した錯イオンを形成するものが多い。
② イオンや化合物は、有色のものが多い。
③ 原子の最外殻電子の数は、族の番号に一致する。
④ 融点が高く、密度が大きい単体が多い。
⑤ 酸化数+6以上の原子を含む化合物が存在する。
共通テスト(旧センター試験)過去問解説 化学 2016年追試 第3問 問1 無機化学の知識問題

単元:
#化学#化学理論#大学入試過去問(化学)#電池と電気分解#共通テスト#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
身のまわりにある元素の単体と化合物に関する記述として下線部に誤りを含 むものを、次の①~⑤のうちから一つ選べ。
① 酸化カルシウムは、水と反応して発熱するため、
携帯用の加熱剤に用いられる。
② 酸化アルミニウムは、ルビーやサファイアの主成分である。
③ 酸化チタン(IV)は、光触媒としての性質をもつため、有機物の汚れなどを分解するために利用される。
④ ヘリウムは、常温で水素についで密度が小さく、飛行船の浮揚ガスに用いられる。
⑤ 金は、化学的に非常に安定であるが、熱濃硫酸には溶ける。
この動画を見る
身のまわりにある元素の単体と化合物に関する記述として下線部に誤りを含 むものを、次の①~⑤のうちから一つ選べ。
① 酸化カルシウムは、水と反応して発熱するため、
携帯用の加熱剤に用いられる。
② 酸化アルミニウムは、ルビーやサファイアの主成分である。
③ 酸化チタン(IV)は、光触媒としての性質をもつため、有機物の汚れなどを分解するために利用される。
④ ヘリウムは、常温で水素についで密度が小さく、飛行船の浮揚ガスに用いられる。
⑤ 金は、化学的に非常に安定であるが、熱濃硫酸には溶ける。
1分で解いてほしい化学計算問題 (28) 難溶性塩の溶解量

単元:
#化学#化学基礎2ー物質の変化#物質量と濃度#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
[2022年 東京電機大学]
塩化銀の飽和水溶液$1.0L$に溶けている塩化銀の質量$(g)$を有効数字2桁で求めよ。
ただし、原子量は$CI=35.5, Ag=108$とし、
塩化銀の溶解度積は$Ksp=8.1×10-11 (mol/L)^2$とする。
この動画を見る
[2022年 東京電機大学]
塩化銀の飽和水溶液$1.0L$に溶けている塩化銀の質量$(g)$を有効数字2桁で求めよ。
ただし、原子量は$CI=35.5, Ag=108$とし、
塩化銀の溶解度積は$Ksp=8.1×10-11 (mol/L)^2$とする。
無機化学第25回 鉄・クロム・マンガン

有機化学第28回 フェノール類

共通テスト(旧センター試験)過去問解説 化学 2016年追試 第2問 問6 鉛蓄電池
単元:
#化学#化学理論#大学入試過去問(化学)#電池と電気分解#共通テスト#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
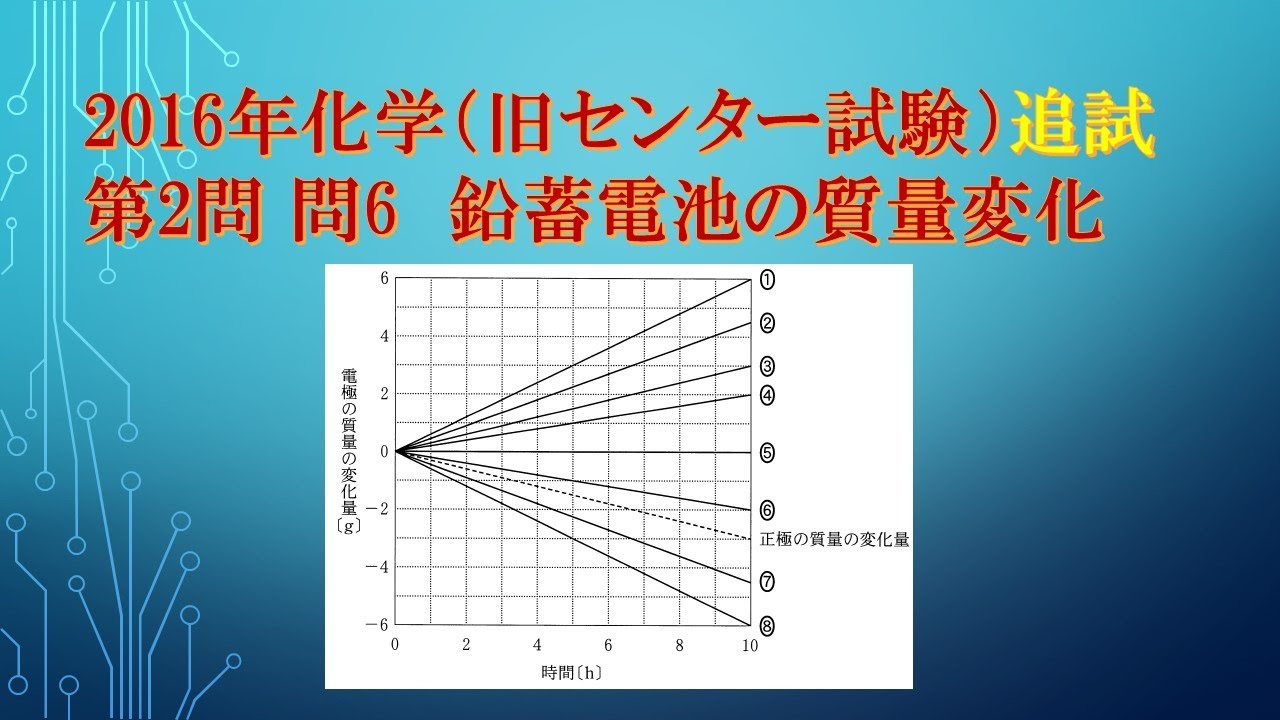
鉛蓄電池に関する次の問い(a・b)に答えよ。
次の文章中のア~ウに当てはまる語句と数値の組合せとして 正しいものを、下の①~⑥のうちから一つ選べ。
鉛蓄電池の放電時には正極で$PbO_2$が$PbSO_4$になる
$\boxed{ ア }$ 反応が起こり、負極で$Pb$が$PbSO_4$になる
$\boxed{ イ }$ 反応が起こる。
正極で$1mol$の $PbSO_4$が生成するとき、 $\boxed{ ウ } mol$の電子が流れる。
※表は動画内参照
この動画を見る
鉛蓄電池に関する次の問い(a・b)に答えよ。
次の文章中のア~ウに当てはまる語句と数値の組合せとして 正しいものを、下の①~⑥のうちから一つ選べ。
鉛蓄電池の放電時には正極で$PbO_2$が$PbSO_4$になる
$\boxed{ ア }$ 反応が起こり、負極で$Pb$が$PbSO_4$になる
$\boxed{ イ }$ 反応が起こる。
正極で$1mol$の $PbSO_4$が生成するとき、 $\boxed{ ウ } mol$の電子が流れる。
※表は動画内参照
1分で解いてほしい化学計算問題 (27) 炭酸カルシウムの純度

単元:
#化学#化学基礎2ー物質の変化#物質量と濃度#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
[2023年 愛知医科大学(改)]
炭酸カルシウム$CaCO_3$を主成分とする大理石$12.0g$に$1.00mol/L$の塩酸を少しずつ加えていくと二酸化炭素が発生し、加えた塩酸の体積が$200mL$になった時点で、二酸化炭素の発生がとまった。
ただし、二酸化炭素は炭酸カルシウムと塩酸の反応でのみ発生し、大理石中の他の成分は塩酸と反応しないものとする。
大理石の炭酸カルシウムの純度(質量百分率)は何$%$か。
有効数字3桁で答えよ。
$CaCO_3$の式量:$100$
この動画を見る
[2023年 愛知医科大学(改)]
炭酸カルシウム$CaCO_3$を主成分とする大理石$12.0g$に$1.00mol/L$の塩酸を少しずつ加えていくと二酸化炭素が発生し、加えた塩酸の体積が$200mL$になった時点で、二酸化炭素の発生がとまった。
ただし、二酸化炭素は炭酸カルシウムと塩酸の反応でのみ発生し、大理石中の他の成分は塩酸と反応しないものとする。
大理石の炭酸カルシウムの純度(質量百分率)は何$%$か。
有効数字3桁で答えよ。
$CaCO_3$の式量:$100$
共通テスト(旧センター試験)過去問解説 化学 2016年追試 第2問 問6 電気分解の量的関係
単元:
#化学#化学理論#大学入試過去問(化学)#電池と電気分解#共通テスト#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
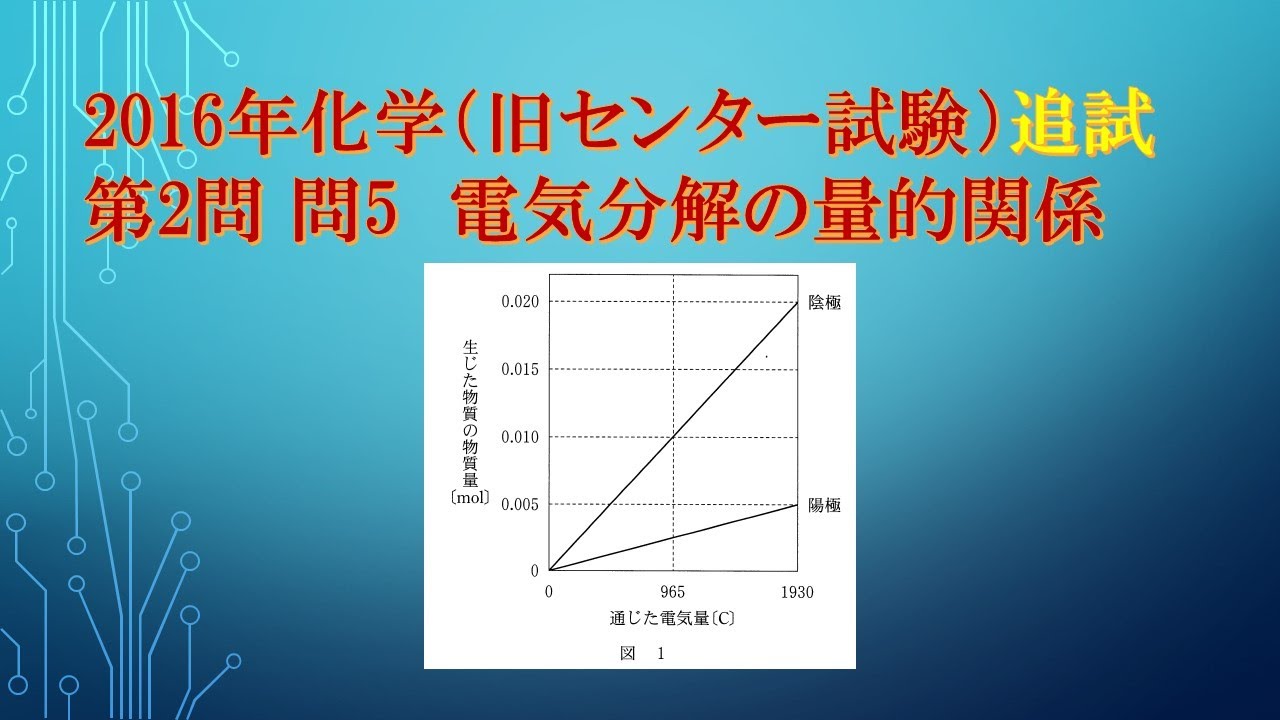
ある電解質$A$の水溶液を、白金電極を用いて電気分解したところ、通じた電気量と両極で生じた物質の物質量との関係が図のようになった。
電解質$A$として最も適当なものを、下の①~⑤のうちから一つ選べ。
①$NaCH$
②$Na_2SO_4$
③$KCI$
④$CuCI_2$
⑤$AgNO_3$
※図は動画内参照
この動画を見る
ある電解質$A$の水溶液を、白金電極を用いて電気分解したところ、通じた電気量と両極で生じた物質の物質量との関係が図のようになった。
電解質$A$として最も適当なものを、下の①~⑤のうちから一つ選べ。
①$NaCH$
②$Na_2SO_4$
③$KCI$
④$CuCI_2$
⑤$AgNO_3$
※図は動画内参照
共通テスト(旧センター試験)過去問解説 化学 2016年追試 第2問 問6 電気分解の量的関係

単元:
#化学#化学理論#大学入試過去問(化学)#電池と電気分解#共通テスト#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
ある電解質Aの水溶液を、白金電極を用いて電気分解したところ、通じた電気量と両極で生じた物質の物質量との関係が図1のようになった。
電解質Aとして最も適当なものを、下の①~⑤のうちから一つ選べ。
①$NaOH$
②$NA_2SO_4$
③$KCI$
④$CuCI_2$
⑤$AgNO_3$
※図は動画内参照
この動画を見る
ある電解質Aの水溶液を、白金電極を用いて電気分解したところ、通じた電気量と両極で生じた物質の物質量との関係が図1のようになった。
電解質Aとして最も適当なものを、下の①~⑤のうちから一つ選べ。
①$NaOH$
②$NA_2SO_4$
③$KCI$
④$CuCI_2$
⑤$AgNO_3$
※図は動画内参照
1分で解いてほしい化学計算問題 (26) 電気分解

単元:
#化学#化学理論#電池と電気分解#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
〔2023年 神戸女学院大学(改)〕
陽極に不純物を含む粗銅版を使用し、硫酸酸性の硫酸銅(Ⅱ)水溶液を$5.0A$の電流で$1.93 \times 10^3$秒電気分解した。
析出した銅の質量$〔g〕$はいくらか。
ファラデー定数を$9.65 \times 10^4C/mol$とする。
この動画を見る
〔2023年 神戸女学院大学(改)〕
陽極に不純物を含む粗銅版を使用し、硫酸酸性の硫酸銅(Ⅱ)水溶液を$5.0A$の電流で$1.93 \times 10^3$秒電気分解した。
析出した銅の質量$〔g〕$はいくらか。
ファラデー定数を$9.65 \times 10^4C/mol$とする。
共通テスト(旧センター試験)過去問解説 化学 2016年追試 第2問 問4 中和反応後のpH

単元:
#化学#化学基礎2ー物質の変化#大学入試過去問(化学)#酸と塩基・水素イオン濃度#共通テスト#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
濃度不明の塩酸$1.0L$を$0.030mol/L$の水酸化ナトリウム水溶液$1.0L$と混合したところ、$0.56kJ$の発熱があった。
この混合溶液の$pH$として最も適当な数値を①~⑧のうちから一つ選べ。
ただし、中和熱は$56kJ/mol$とし、中和反応以外による発熱または吸熱は無視できるものとする。
①$1$ ②$2$ ③$3$ ④$5$ ⑤$9$ ⑥$11$ ⑦$12$ ⑧$13$
この動画を見る
濃度不明の塩酸$1.0L$を$0.030mol/L$の水酸化ナトリウム水溶液$1.0L$と混合したところ、$0.56kJ$の発熱があった。
この混合溶液の$pH$として最も適当な数値を①~⑧のうちから一つ選べ。
ただし、中和熱は$56kJ/mol$とし、中和反応以外による発熱または吸熱は無視できるものとする。
①$1$ ②$2$ ③$3$ ④$5$ ⑤$9$ ⑥$11$ ⑦$12$ ⑧$13$
無機化学第24回 銅と銀

有機化学第27回 配向性



