 雙葉中学
雙葉中学
 雙葉中学
雙葉中学
2025年雙葉中入試算数大問① 中学受験指導歴20年以上プロ塾講師のじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#雙葉中学
指導講師:
重吉
問題文全文(内容文):
[ 1] ア ~キにあてはまる数を書きましょう。(式と計算と答え)
(2) 右の図は半円を組み合わせたものです。3つの半円の中心は同じで、半径の比は、1:2:3です。
1番大きい円の半径が9cmのとき、かげをつけた部分の周りの長さは合計で イ cmです。
※図は動画内参照
(3) 日本で使われる部屋の広さを表す単位として「帖」があります。1帖は、 そうじ 1.62 m²です。掃除ロボットAは、6帖を掃除するのに27分かかり、 掃除ロボットBは、10帖を掃除するのに30分かかります。2つのロボットA、B が同時に 37.44m² の部屋を掃除するのに ウ分 エ秒かかります。
(4)下の表は、40人の生徒が50点満点のテストを受けた結果を表したものです。
※図は動画内参照
中央値が35点、最頻値が40点、平均値はキ点でした。
この動画を見る
[ 1] ア ~キにあてはまる数を書きましょう。(式と計算と答え)
(2) 右の図は半円を組み合わせたものです。3つの半円の中心は同じで、半径の比は、1:2:3です。
1番大きい円の半径が9cmのとき、かげをつけた部分の周りの長さは合計で イ cmです。
※図は動画内参照
(3) 日本で使われる部屋の広さを表す単位として「帖」があります。1帖は、 そうじ 1.62 m²です。掃除ロボットAは、6帖を掃除するのに27分かかり、 掃除ロボットBは、10帖を掃除するのに30分かかります。2つのロボットA、B が同時に 37.44m² の部屋を掃除するのに ウ分 エ秒かかります。
(4)下の表は、40人の生徒が50点満点のテストを受けた結果を表したものです。
※図は動画内参照
中央値が35点、最頻値が40点、平均値はキ点でした。
2024年雙葉中算数大問②、③中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#単位・比と割合・比例・反比例#立体図形#立体図形その他#速さ#速さその他#雙葉中学
指導講師:
重吉
問題文全文(内容文):
[2] たて630mm、横1470mm、高さ1260mmの直方体の箱があります。この箱に同じ大きさの直方体のブロックを、図の向きに、箱がいっぱいになるまですき間なく入れていきます。ブロックのたて、横、高さの比は1:14:5です。 箱の中のブロックの数が最も少なくなるときのブロックのたて、横、高さはそれぞれ何mmですか。また、そのときのブロックの数は何個ですか。 箱の厚さは考えません。(式と計算と答え)
[3] 下流にあるA地点と上流にあるB地点は、5733m離れています。兄はボートをこいでA地点を出発し、B地点に着いたら折り返し、2時間後にA地点に戻ってきました。静水時の兄がこぐボートの速さと川の流れの速さは一定で、その比は 10:3です。(式と計算と答え)
(1) 兄はA地点を出発してから、何時間何分後にB地点に着きましたか。
(2) 川の流れの速さは分速何mですか。
(3) 兄がA地点を出発したのと同時に、弟もボートでB地点を出発しました。 弟は、ボートをこがずに川の流れにまかせて進み、兄と2回出会ってA地点に着きました。弟が2回目に兄と出会うのは、2人が出発してから何時間何分何秒後でしたか。
この動画を見る
[2] たて630mm、横1470mm、高さ1260mmの直方体の箱があります。この箱に同じ大きさの直方体のブロックを、図の向きに、箱がいっぱいになるまですき間なく入れていきます。ブロックのたて、横、高さの比は1:14:5です。 箱の中のブロックの数が最も少なくなるときのブロックのたて、横、高さはそれぞれ何mmですか。また、そのときのブロックの数は何個ですか。 箱の厚さは考えません。(式と計算と答え)
[3] 下流にあるA地点と上流にあるB地点は、5733m離れています。兄はボートをこいでA地点を出発し、B地点に着いたら折り返し、2時間後にA地点に戻ってきました。静水時の兄がこぐボートの速さと川の流れの速さは一定で、その比は 10:3です。(式と計算と答え)
(1) 兄はA地点を出発してから、何時間何分後にB地点に着きましたか。
(2) 川の流れの速さは分速何mですか。
(3) 兄がA地点を出発したのと同時に、弟もボートでB地点を出発しました。 弟は、ボートをこがずに川の流れにまかせて進み、兄と2回出会ってA地点に着きました。弟が2回目に兄と出会うのは、2人が出発してから何時間何分何秒後でしたか。
2024年雙葉中算数大問①(1)~(4)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他#過去問解説(学校別)#文章題#売買損益と食塩水#平面図形#角度と面積#雙葉中学
指導講師:
重吉
問題文全文(内容文):
$\boxed{ ア }~\boxed{ エ}$に入る数を書きましょう
(1)
$21.6\times\dfrac{9}{25}-2.16\times\boxed{ ア }+0.216\times0.25=4.86$
(2)
$\dfrac{1}{◎\times (◎+1)}=\dfrac{1}{◎}-\dfrac{1}{◎+1}$が成り立ちます。たとえば、$\dfrac{1}{3\times4}=\dfrac{1}{3}-\dfrac{1}{4}$です。これを利用すると、
$\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{110}=\boxed{ イ }$
(3)
右の図は、正方形と円、おうぎ形を組みあわせたものです。正方形の対角線の長さは4 cmです。影を付けた部分の面積は$\boxed{ ウ }$㎠です。
(4)
仕入れ値が110円の商品を217個仕入れ、5割の利益を見込んで定価を付けました。定価で$\boxed{ エ }$個売ったところ、売れなくなったので定価の二割引きで売りました。全部売り切り、利益は7810円でした。
この動画を見る
$\boxed{ ア }~\boxed{ エ}$に入る数を書きましょう
(1)
$21.6\times\dfrac{9}{25}-2.16\times\boxed{ ア }+0.216\times0.25=4.86$
(2)
$\dfrac{1}{◎\times (◎+1)}=\dfrac{1}{◎}-\dfrac{1}{◎+1}$が成り立ちます。たとえば、$\dfrac{1}{3\times4}=\dfrac{1}{3}-\dfrac{1}{4}$です。これを利用すると、
$\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{110}=\boxed{ イ }$
(3)
右の図は、正方形と円、おうぎ形を組みあわせたものです。正方形の対角線の長さは4 cmです。影を付けた部分の面積は$\boxed{ ウ }$㎠です。
(4)
仕入れ値が110円の商品を217個仕入れ、5割の利益を見込んで定価を付けました。定価で$\boxed{ エ }$個売ったところ、売れなくなったので定価の二割引きで売りました。全部売り切り、利益は7810円でした。
雙葉中2024年算数入試問題「流水算」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#速さ#旅人算・通過算・流水算#雙葉中学
指導講師:
重吉
問題文全文(内容文):
下流にあるA地点と上流にあるB地点は、5733m離れています。
兄はボートをこいでA地点を出発し、B地点に着いたら折り返し、2時間後にA地点に戻ってきました。
静水時の兄がこぐボートの速さと川の流れの速さは一定で、その日は10:3です。(式と計算と答え)
(1)
兄はA地点を出発してから、何時間何分後にB地点に着きましたか。
(2)
川の流れの速さは分速何mですか。
(3)
兄がA地点を出発したのと同時に、弟もボートでB地点を出発しました。
弟は、ボートをこがずに川の流れまかせて進み、兄と2回出会ってA地点に着きました。
弟が2回目に兄と出会うのは、2人が出発してから何時間何分何秒後でしたか。
出典:2024年雙葉中学校 入試問題
この動画を見る
下流にあるA地点と上流にあるB地点は、5733m離れています。
兄はボートをこいでA地点を出発し、B地点に着いたら折り返し、2時間後にA地点に戻ってきました。
静水時の兄がこぐボートの速さと川の流れの速さは一定で、その日は10:3です。(式と計算と答え)
(1)
兄はA地点を出発してから、何時間何分後にB地点に着きましたか。
(2)
川の流れの速さは分速何mですか。
(3)
兄がA地点を出発したのと同時に、弟もボートでB地点を出発しました。
弟は、ボートをこがずに川の流れまかせて進み、兄と2回出会ってA地点に着きました。
弟が2回目に兄と出会うのは、2人が出発してから何時間何分何秒後でしたか。
出典:2024年雙葉中学校 入試問題
落とせば合格赤信号!2024女子御三家(桜蔭、女子学院、雙葉)計算問題5題」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#女子学院中学#桜蔭中学#雙葉中学
指導講師:
重吉
問題文全文(内容文):
【2024年桜蔭中】
$16- ${$ 7 \displaystyle \frac{1}{3} \times 2.2-(5.7-4\displaystyle \frac{1}{6})\div 3\displaystyle \frac{2}{7} $}$=□$
$16-${$ \displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□}-(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\div \displaystyle \frac{□}{□}$ }
$=16-${$ \displaystyle \frac{□}{□} -(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\times \displaystyle \frac{□}{□}$ }
$=16- (\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□})$
$=16-(\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□})$
$=16-\displaystyle \frac{□}{□} =\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□}=\displaystyle \frac{□}{□}$
この動画を見る
【2024年桜蔭中】
$16- ${$ 7 \displaystyle \frac{1}{3} \times 2.2-(5.7-4\displaystyle \frac{1}{6})\div 3\displaystyle \frac{2}{7} $}$=□$
$16-${$ \displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□}-(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\div \displaystyle \frac{□}{□}$ }
$=16-${$ \displaystyle \frac{□}{□} -(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\times \displaystyle \frac{□}{□}$ }
$=16- (\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□})$
$=16-(\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□})$
$=16-\displaystyle \frac{□}{□} =\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□}=\displaystyle \frac{□}{□}$
雙葉中学校2023年計算問題

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#雙葉中学
指導講師:
重吉
問題文全文(内容文):
雙葉中学校2023年計算問題
$3 \displaystyle \frac{2}{5} \times (3 \displaystyle \frac{11}{12} + \displaystyle \frac{1}{3}) \div $㋐ $=20.33$
㋐を求めよ
この動画を見る
雙葉中学校2023年計算問題
$3 \displaystyle \frac{2}{5} \times (3 \displaystyle \frac{11}{12} + \displaystyle \frac{1}{3}) \div $㋐ $=20.33$
㋐を求めよ
雙葉中学校2023年「円周、速さ」

単元:
#算数(中学受験)#過去問解説(学校別)#速さ#速さその他#雙葉中学
指導講師:
重吉
問題文全文(内容文):
雙葉中学校2023年「円周、速さ」
-----------------
(1)ゴンドラが48°動くのに1分24秒、1周360°は147mあります。
ゴンドラが1周回るのは分速何mになるか求めよ
(2)ゴンドラが頂上を18秒ごとに通過する
1周で頂上をゴンドラが何台通過するか求めよ
この動画を見る
雙葉中学校2023年「円周、速さ」
-----------------
(1)ゴンドラが48°動くのに1分24秒、1周360°は147mあります。
ゴンドラが1周回るのは分速何mになるか求めよ
(2)ゴンドラが頂上を18秒ごとに通過する
1周で頂上をゴンドラが何台通過するか求めよ
これ解ける小学生は頭がどうかしてる!あまりにも難しすぎた1問!ノーヒントで解けたら天才だと思う【中学受験算数】【入試問題】【渋谷教育学園渋谷中学校】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#渋谷教育学園渋谷中学#雙葉中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022年雙葉中学校
左図は,正方形とおうぎ形を組み合わせたものです。
正方形の面積が32㎠のとき斜線部分の面積は?
(円周率3.14)
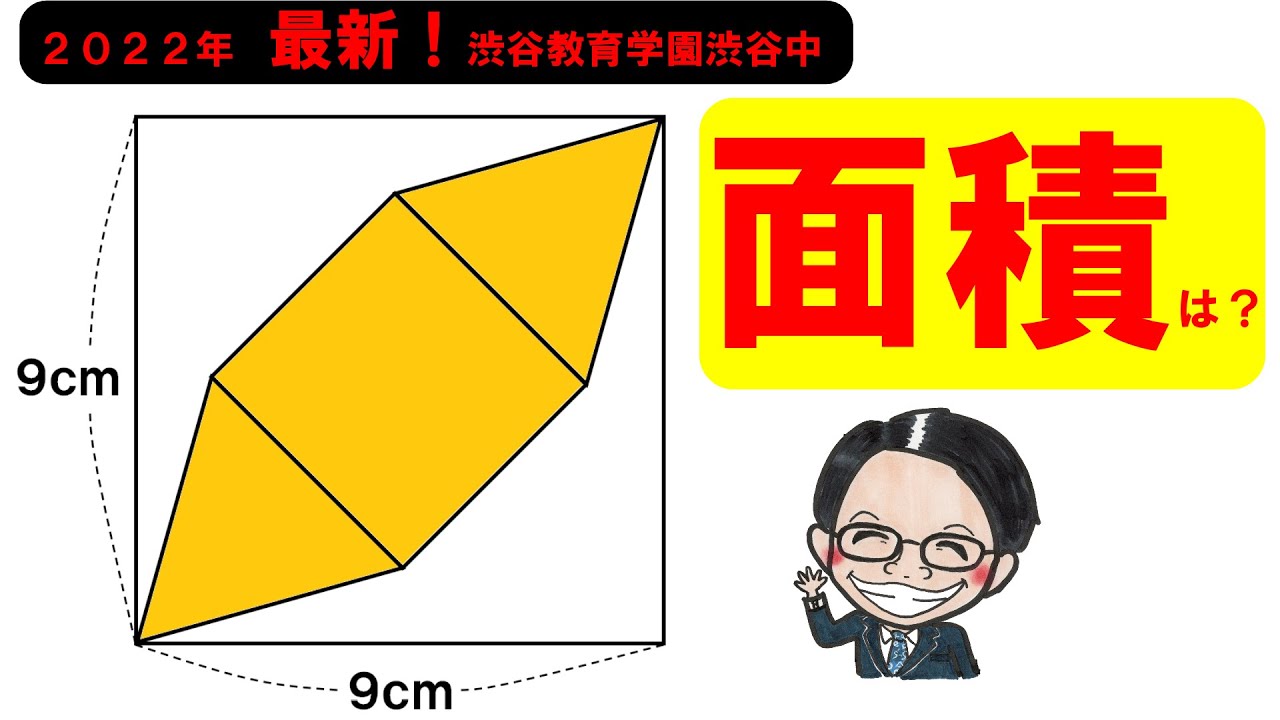
2022渋谷教育学園渋谷中学校
左図のように1辺の長さが9cmの正方形の中に2つの正三角形と正方形が入っています。
色がついた部分の面積は?
*図は動画内参照
この動画を見る
2022年雙葉中学校
左図は,正方形とおうぎ形を組み合わせたものです。
正方形の面積が32㎠のとき斜線部分の面積は?
(円周率3.14)
2022渋谷教育学園渋谷中学校
左図のように1辺の長さが9cmの正方形の中に2つの正三角形と正方形が入っています。
色がついた部分の面積は?
*図は動画内参照
