 桜蔭中学
桜蔭中学
 桜蔭中学
桜蔭中学
2025年桜蔭中入試算数大問① 中学受験指導歴20年プロのじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#桜蔭中学
指導講師:
重吉
問題文全文(内容文):
大問1
(1)
\[
\left( \frac{15}{7} + 0.6 \right) \times \boxed{\text{ア}} + 6 \frac{7}{13} - \frac{19}{91} = 9
\]
(2) 底面が正方形の直方体Pと、円柱Qがあります。2つの立体の高さは同じです。図のように、 直方体Pには底面のAからBへ、円柱Qには底面のCからDへ、長さが最も短くなるように側面を1周させて糸を巻きつけたところ、2つの立体に巻きつけた糸の長さは同じとなりました。
① 直方体Pの底面の1辺の長さは、円柱Qの底面の半径の$\boxed{\text{イ}}$倍です。
② 直方体Pの体積は、円柱の体積の$\boxed{\text{ウ}}$倍です。
※図は動画内参照
(3) ある整数nを4で割った余りを(n),7で割った余りを [n] と表すことにします。
たとえば、 6÷4 = 1 余り2なので(6)=2
6÷7 = 0 余り6なので [6] =6 です。
① (n)= 3 である1以上の整数nについて考えます。
小さい順に並べたとき、2025番目に来る数は$\boxed{\text{エ}}$です。また、1番目から2025番目までの数のうち、 [n] = 5 となる数は $\boxed{\text{オ}}$個あります。
② 1から100までの整数のうち、 (n)= [n] となる整数は $\boxed{\text{カ}}$個あります。
この動画を見る
大問1
(1)
\[
\left( \frac{15}{7} + 0.6 \right) \times \boxed{\text{ア}} + 6 \frac{7}{13} - \frac{19}{91} = 9
\]
(2) 底面が正方形の直方体Pと、円柱Qがあります。2つの立体の高さは同じです。図のように、 直方体Pには底面のAからBへ、円柱Qには底面のCからDへ、長さが最も短くなるように側面を1周させて糸を巻きつけたところ、2つの立体に巻きつけた糸の長さは同じとなりました。
① 直方体Pの底面の1辺の長さは、円柱Qの底面の半径の$\boxed{\text{イ}}$倍です。
② 直方体Pの体積は、円柱の体積の$\boxed{\text{ウ}}$倍です。
※図は動画内参照
(3) ある整数nを4で割った余りを(n),7で割った余りを [n] と表すことにします。
たとえば、 6÷4 = 1 余り2なので(6)=2
6÷7 = 0 余り6なので [6] =6 です。
① (n)= 3 である1以上の整数nについて考えます。
小さい順に並べたとき、2025番目に来る数は$\boxed{\text{エ}}$です。また、1番目から2025番目までの数のうち、 [n] = 5 となる数は $\boxed{\text{オ}}$個あります。
② 1から100までの整数のうち、 (n)= [n] となる整数は $\boxed{\text{カ}}$個あります。
2024年桜蔭中算数大問①(1)~(3)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#平面図形#角度と面積#場合の数#場合の数#桜蔭中学
指導講師:
重吉
問題文全文(内容文):
Ⅰ
(1)①16-{7(1/3)×2.2-(5.7-4(1/6)÷3(2/7))}=㋐
②5.75-3/2÷(15/26-㋑×1.35)=2(1/28)
(2) 黒い丸●と白い丸○を右の(例)のように、縦7マスすべてに並べます。
① 並べ方のきまりは次の(あ) (い) (う) (え)です。
(あ) 上から2マス目と上から4マス目には同じ色の丸は並べない。
(い) 上から2マス目と上から6マス目には同じ色の丸を並べる。
(う) 下から3マスすべてに同じ色の丸を並べることはできない。
(え) 上から4マス目が白い丸のとき、上から3マス目と上から5マス目の両方ともに黒い丸を並べることはできない。
(3マス目,5マス目のどちらか一方に黒い丸を並べることはできる)
このとき、黒い丸と白い丸の並べ方は全部で㋒通りあります。
② 縦7マスを右のように4列並べます。①の(あ) (い) (う) (え)のきまりに次の(お)のきまりを加えて、黒い丸と白い丸をこの28マスに並べるとき、 並べ方は全部で㋓通りあります。
(お) 各列の上から2マス目のA, B, C, DにはAとDに同じ色の丸, BとCに同じ色の丸を並べる。また、AとBには同じ色の丸を並べない。
(3) 図1のような1辺の長さが10cmの正方形の折り紙を、1本の対角線で折ると図2のようになります。図2の直角二等辺三角形を,45°の角をもつ頂点が重なるように折ると図3のようになります。 図3の直角二等辺三角形を、直角が3等分になるように折ると、順に図4、図5のようになります。 図5の折り紙を直線ABにそって切ると図6のようになります。ただし、図の (細い直線) は折り目を表します。
※図は動画内参照
① 図6の折り紙を広げたときの図形の名前は㋔です。
② 図6のABの長さをはかると2.7cmでした。図6の折り紙を広げたときの図形の面積は㋕cm²です。
③ 右の図7のように、図6の三角形ABCの内部から1辺の長さが 0.6cmの正方形を切りぬきます。さらに、中心が辺BC上にある直径1cmの半円を切り取ります。図7の折り紙を広げたとき、 残った部分の面積は㋖cm²です。
この動画を見る
Ⅰ
(1)①16-{7(1/3)×2.2-(5.7-4(1/6)÷3(2/7))}=㋐
②5.75-3/2÷(15/26-㋑×1.35)=2(1/28)
(2) 黒い丸●と白い丸○を右の(例)のように、縦7マスすべてに並べます。
① 並べ方のきまりは次の(あ) (い) (う) (え)です。
(あ) 上から2マス目と上から4マス目には同じ色の丸は並べない。
(い) 上から2マス目と上から6マス目には同じ色の丸を並べる。
(う) 下から3マスすべてに同じ色の丸を並べることはできない。
(え) 上から4マス目が白い丸のとき、上から3マス目と上から5マス目の両方ともに黒い丸を並べることはできない。
(3マス目,5マス目のどちらか一方に黒い丸を並べることはできる)
このとき、黒い丸と白い丸の並べ方は全部で㋒通りあります。
② 縦7マスを右のように4列並べます。①の(あ) (い) (う) (え)のきまりに次の(お)のきまりを加えて、黒い丸と白い丸をこの28マスに並べるとき、 並べ方は全部で㋓通りあります。
(お) 各列の上から2マス目のA, B, C, DにはAとDに同じ色の丸, BとCに同じ色の丸を並べる。また、AとBには同じ色の丸を並べない。
(3) 図1のような1辺の長さが10cmの正方形の折り紙を、1本の対角線で折ると図2のようになります。図2の直角二等辺三角形を,45°の角をもつ頂点が重なるように折ると図3のようになります。 図3の直角二等辺三角形を、直角が3等分になるように折ると、順に図4、図5のようになります。 図5の折り紙を直線ABにそって切ると図6のようになります。ただし、図の (細い直線) は折り目を表します。
※図は動画内参照
① 図6の折り紙を広げたときの図形の名前は㋔です。
② 図6のABの長さをはかると2.7cmでした。図6の折り紙を広げたときの図形の面積は㋕cm²です。
③ 右の図7のように、図6の三角形ABCの内部から1辺の長さが 0.6cmの正方形を切りぬきます。さらに、中心が辺BC上にある直径1cmの半円を切り取ります。図7の折り紙を広げたとき、 残った部分の面積は㋖cm²です。
落とせば合格赤信号!2024女子御三家(桜蔭、女子学院、雙葉)計算問題5題」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#女子学院中学#桜蔭中学#雙葉中学
指導講師:
重吉
問題文全文(内容文):
【2024年桜蔭中】
$16- ${$ 7 \displaystyle \frac{1}{3} \times 2.2-(5.7-4\displaystyle \frac{1}{6})\div 3\displaystyle \frac{2}{7} $}$=□$
$16-${$ \displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□}-(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\div \displaystyle \frac{□}{□}$ }
$=16-${$ \displaystyle \frac{□}{□} -(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\times \displaystyle \frac{□}{□}$ }
$=16- (\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□})$
$=16-(\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□})$
$=16-\displaystyle \frac{□}{□} =\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□}=\displaystyle \frac{□}{□}$
この動画を見る
【2024年桜蔭中】
$16- ${$ 7 \displaystyle \frac{1}{3} \times 2.2-(5.7-4\displaystyle \frac{1}{6})\div 3\displaystyle \frac{2}{7} $}$=□$
$16-${$ \displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□}-(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\div \displaystyle \frac{□}{□}$ }
$=16-${$ \displaystyle \frac{□}{□} -(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\times \displaystyle \frac{□}{□}$ }
$=16- (\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□})$
$=16-(\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□})$
$=16-\displaystyle \frac{□}{□} =\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□}=\displaystyle \frac{□}{□}$
桜蔭中学校2023年入試算数「計算問題」

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#桜蔭中学
指導講師:
重吉
問題文全文(内容文):
桜蔭中学校2023年入試算数「計算問題」
$0.003 \times 4 + ㋐ \times 4 + 2\displaystyle \frac{37}{54} = 2\displaystyle \frac{106}{135}$
この動画を見る
桜蔭中学校2023年入試算数「計算問題」
$0.003 \times 4 + ㋐ \times 4 + 2\displaystyle \frac{37}{54} = 2\displaystyle \frac{106}{135}$
2022年桜蔭中学校&女子学院中学校の入試問題「四則計算」

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#女子学院中学#桜蔭中学
指導講師:
重吉
問題文全文(内容文):
2022年桜蔭中学校&女子学院中学校の入試問題「四則計算」
-----------------
(1)
$13 \displaystyle \frac{1}{3} - ${$(4\displaystyle \frac{13}{14} \times □-2.375) \div 1\displaystyle \frac{2}{11}-3\displaystyle \frac{5}{7}$}$=5\displaystyle \frac{11}{24}$
(2)
$5\displaystyle \frac{2}{3} \div 0.85 \times \displaystyle \frac{37}{4} \times \displaystyle \frac{17}{25} - (\displaystyle \frac{13}{15} +5.25)=□$
$\displaystyle \frac{□}{□} \div \displaystyle \frac{□}{□} \times \displaystyle \frac{37}{4} \times \displaystyle \frac{17}{25} - (\displaystyle \frac{13}{15} + \displaystyle \frac{□}{□})$
この動画を見る
2022年桜蔭中学校&女子学院中学校の入試問題「四則計算」
-----------------
(1)
$13 \displaystyle \frac{1}{3} - ${$(4\displaystyle \frac{13}{14} \times □-2.375) \div 1\displaystyle \frac{2}{11}-3\displaystyle \frac{5}{7}$}$=5\displaystyle \frac{11}{24}$
(2)
$5\displaystyle \frac{2}{3} \div 0.85 \times \displaystyle \frac{37}{4} \times \displaystyle \frac{17}{25} - (\displaystyle \frac{13}{15} +5.25)=□$
$\displaystyle \frac{□}{□} \div \displaystyle \frac{□}{□} \times \displaystyle \frac{37}{4} \times \displaystyle \frac{17}{25} - (\displaystyle \frac{13}{15} + \displaystyle \frac{□}{□})$
ある条件を見逃すと一生解けない!?誰もが見逃しやすいその条件は○○【中学受験算数】【入試問題】【江戸川女子中学校】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#ラ・サール中学#桜蔭中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2021城西川越中学校
下図のlとmは平行で、三角形ABCは正三角形です。
角㋐は何度?
2021桐蔭学園中等教育学校
下図の印がついた角の大きさの合計は何度?
2021ラ・サール中学校
下図で、ADとBCが平行、AE=BE、BC=BDです。
角㋐、角㋑は何度?
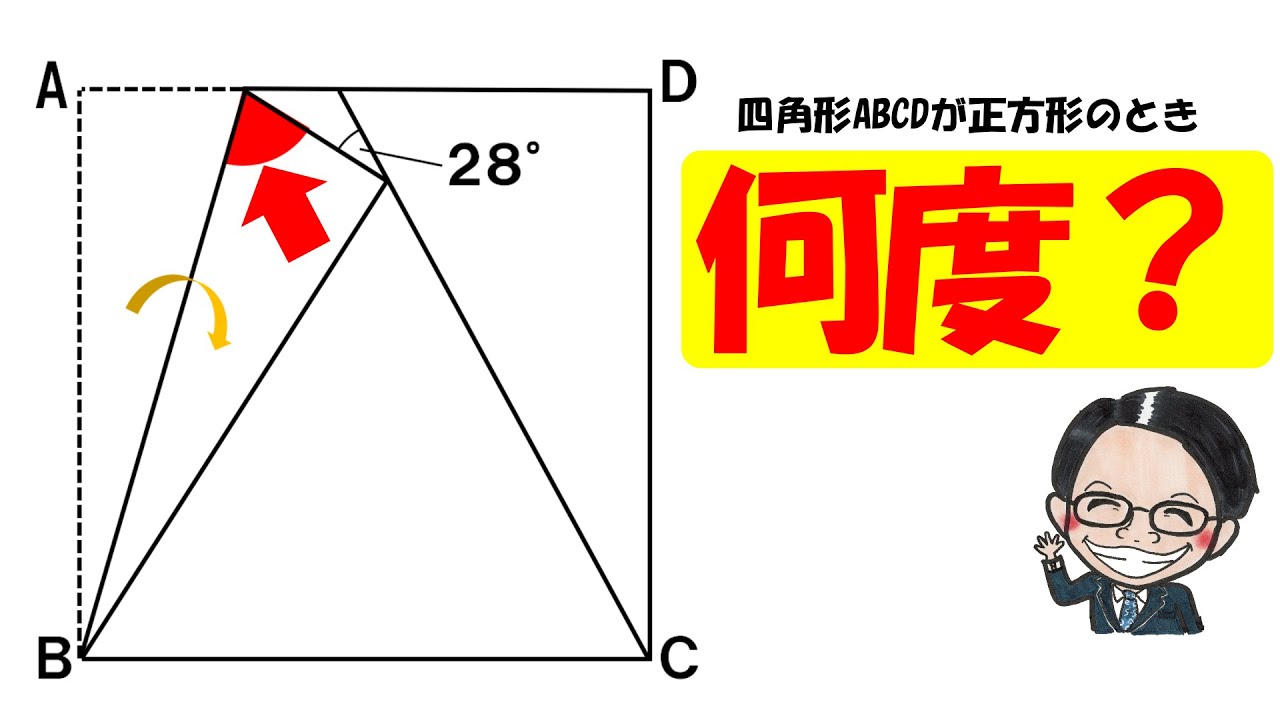
2021江戸川女子中学校
下図は正方形を折り返したところを表している。角㋐は何度?
*図は動画内参照
この動画を見る
2021城西川越中学校
下図のlとmは平行で、三角形ABCは正三角形です。
角㋐は何度?
2021桐蔭学園中等教育学校
下図の印がついた角の大きさの合計は何度?
2021ラ・サール中学校
下図で、ADとBCが平行、AE=BE、BC=BDです。
角㋐、角㋑は何度?
2021江戸川女子中学校
下図は正方形を折り返したところを表している。角㋐は何度?
*図は動画内参照
