 売買損益と食塩水
売買損益と食塩水
 売買損益と食塩水
売買損益と食塩水
2024年慶應義塾湘南藤沢中算数大問①② 中学受験指導20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#文章題#売買損益と食塩水#平面図形#角度と面積#速さ#旅人算・通過算・流水算#慶應義塾湘南藤沢中等部
指導講師:
重吉
問題文全文(内容文):
【1】$\boxed{ア}$, $\boxed{イ}$, $\boxed{ウ}$にあてはまる数を求めなさい。
(1)$10-(20.24+17\dfrac{\boxed{ ア }}{25})\div9=5\dfrac{4}{5}$
(2)$\dfrac{1}{3\times6}+\dfrac{1}{6\times9}+\dfrac{1}{9\times12}+\dfrac{1}{12\times15}+\dfrac{1}{15\times18}=\boxed{イ}$
(3)1から100までの数から4の倍数と6の倍数を除いた数は全部で$\boxed{ウ}$個である。
【2】
(1)1周672 mの池の周りを、K君、O君の二人が同じ地点から同時に出発し、それぞれ一定の速さで歩く。二人が反対方向に歩く場合は6分後に初めて出会い、2人が同じ方向に歩く場合は42分後にK君がO君を初めて追い越す。K君の歩く速さは毎分何mですか。
(2)毎日決まった数だけ売れる1個150円の品物がある。今、売上を20円値上げしたところ、1日の売り上げ個数は1割減少したが、売上高は180円増加した。この品物の、値上げ前の1日の売り上げ個数は何個ですか。
(3)図のような長方形において、角㋐の大きさを求めなさい。
※図は動画内参照
この動画を見る
【1】$\boxed{ア}$, $\boxed{イ}$, $\boxed{ウ}$にあてはまる数を求めなさい。
(1)$10-(20.24+17\dfrac{\boxed{ ア }}{25})\div9=5\dfrac{4}{5}$
(2)$\dfrac{1}{3\times6}+\dfrac{1}{6\times9}+\dfrac{1}{9\times12}+\dfrac{1}{12\times15}+\dfrac{1}{15\times18}=\boxed{イ}$
(3)1から100までの数から4の倍数と6の倍数を除いた数は全部で$\boxed{ウ}$個である。
【2】
(1)1周672 mの池の周りを、K君、O君の二人が同じ地点から同時に出発し、それぞれ一定の速さで歩く。二人が反対方向に歩く場合は6分後に初めて出会い、2人が同じ方向に歩く場合は42分後にK君がO君を初めて追い越す。K君の歩く速さは毎分何mですか。
(2)毎日決まった数だけ売れる1個150円の品物がある。今、売上を20円値上げしたところ、1日の売り上げ個数は1割減少したが、売上高は180円増加した。この品物の、値上げ前の1日の売り上げ個数は何個ですか。
(3)図のような長方形において、角㋐の大きさを求めなさい。
※図は動画内参照
2024年海城中算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#文章題#売買損益と食塩水#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平面図形#角度と面積
指導講師:
重吉
問題文全文(内容文):
(1)
$9\div\{4\dfrac{1}{6}+(2.25-1\dfrac{1}{2})\div0.75-2\dfrac{1}{2}\}\div1.125$を計算しなさい。
(2)
8%の食塩水を80g、6%の食塩水を120g、4%の食塩水を150g、水▭gを混ぜて5%の食塩水を作りました。▭に当てはまる数を求めなさい。
(3)
現在、父の年齢は兄の年齢の3倍と弟の年齢の和より4歳上です。24年後m父の年齢は兄と弟の年齢の和に等しくなります。父と弟の年齢の差を求めなさい。
(4)
100以上300以下の整数のうち、約数の個数が9個である整数をすべて求めなさい。
(5)
下の図において直線ABとCDは平行で、長さの等しい辺には同じ印がついています。図の角アの大きさを求めなさい。
※図は動画内参照図
この動画を見る
(1)
$9\div\{4\dfrac{1}{6}+(2.25-1\dfrac{1}{2})\div0.75-2\dfrac{1}{2}\}\div1.125$を計算しなさい。
(2)
8%の食塩水を80g、6%の食塩水を120g、4%の食塩水を150g、水▭gを混ぜて5%の食塩水を作りました。▭に当てはまる数を求めなさい。
(3)
現在、父の年齢は兄の年齢の3倍と弟の年齢の和より4歳上です。24年後m父の年齢は兄と弟の年齢の和に等しくなります。父と弟の年齢の差を求めなさい。
(4)
100以上300以下の整数のうち、約数の個数が9個である整数をすべて求めなさい。
(5)
下の図において直線ABとCDは平行で、長さの等しい辺には同じ印がついています。図の角アの大きさを求めなさい。
※図は動画内参照図
2024年明治大付属明治中算数「食塩水濃度」中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
重吉
問題文全文(内容文):
容器$A$には6%の食塩水が300g,容器$B$には12%の食塩水が500g入っています.
両方の容器から同じ量の食塩水を同時に取り出し,それぞれもう一方の容器に入れたところ,
$A$に入っている食塩水の濃さは10%になりました.
$B$に入っている食塩水の濃さは$\Box$になります.
$\Box$を求めよ.
2024年明治大付属明治中過去問
この動画を見る
容器$A$には6%の食塩水が300g,容器$B$には12%の食塩水が500g入っています.
両方の容器から同じ量の食塩水を同時に取り出し,それぞれもう一方の容器に入れたところ,
$A$に入っている食塩水の濃さは10%になりました.
$B$に入っている食塩水の濃さは$\Box$になります.
$\Box$を求めよ.
2024年明治大付属明治中過去問
2024年明治大付属明治中算数「食塩水濃度」中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#明治大学附属明治中学
指導講師:
重吉
問題文全文(内容文):
容器Aには6%の食塩水が300g、容器Bには12%の食塩水が500g入っています。
両方の容器から同じ量の食塩水を同時に取り出し、それぞれもう一方の容器に入れたところ、Aに入っている食塩水の濃さは10%になりました。
Bに入っている食塩水の濃さは□%になります。
出典:2024年明治大学付属明治中学校 入試問題
この動画を見る
容器Aには6%の食塩水が300g、容器Bには12%の食塩水が500g入っています。
両方の容器から同じ量の食塩水を同時に取り出し、それぞれもう一方の容器に入れたところ、Aに入っている食塩水の濃さは10%になりました。
Bに入っている食塩水の濃さは□%になります。
出典:2024年明治大学付属明治中学校 入試問題
【予習シリーズ算数・小6上】売買損益と線分図【割合と比の文章題】

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
受験算数の森
問題文全文(内容文):
ある品物を□円で仕入れ、仕入れ値の2割の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の1割引きにしたところ、品物は売れて利益は160円になりました。
この動画を見る
ある品物を□円で仕入れ、仕入れ値の2割の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の1割引きにしたところ、品物は売れて利益は160円になりました。
売買損益算(標準・発展)をサクッと学習しよう!【中学受験算数】【特殊算攻略講座11】

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
こばちゃん塾
問題文全文(内容文):
例題1
ある商品に原価の8割の利益を見込んで定価をつけましたが、売れないので
定価の1300円引きで売ったところ、300円の利益がありました。
この商品の定価は何円ですか。
例題2
あるくだものを50個仕入れ、1個300円の利益を見込んで定価をつけましたが、
そのうちの4割はいたんでいたので、定価の2割引きで売り、
残りは定価で売ったところ11400円の利益がありました。
このくだもの1個の仕入れ値は何円ですか。
例題3
商品を1個▢円で△個仕入れました。
仕入れた商品の8%は売れ残ると予想し全体で5640円の利益が得られるように
1個93円で売ることにしました。
商品を売ったところ、実際は2%の売れ残りで済みました。
その結果、全体で7035円の利益を得ることができました。
▢と△にあてはまる整数をそれぞれ求めましょう。
2020 芝中学校 改題
この動画を見る
例題1
ある商品に原価の8割の利益を見込んで定価をつけましたが、売れないので
定価の1300円引きで売ったところ、300円の利益がありました。
この商品の定価は何円ですか。
例題2
あるくだものを50個仕入れ、1個300円の利益を見込んで定価をつけましたが、
そのうちの4割はいたんでいたので、定価の2割引きで売り、
残りは定価で売ったところ11400円の利益がありました。
このくだもの1個の仕入れ値は何円ですか。
例題3
商品を1個▢円で△個仕入れました。
仕入れた商品の8%は売れ残ると予想し全体で5640円の利益が得られるように
1個93円で売ることにしました。
商品を売ったところ、実際は2%の売れ残りで済みました。
その結果、全体で7035円の利益を得ることができました。
▢と△にあてはまる整数をそれぞれ求めましょう。
2020 芝中学校 改題
濃度算(標準・発展)をサクッと学習しよう!【中学受験算数】【特殊算攻略講座10】

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
こばちゃん塾
問題文全文(内容文):
例題1
2%の食塩水があります。
この食塩水を熱して240gの水を蒸発させると5%の食塩水ができます。
2%の食塩水は何gありますか。
例題2
容器㋐には5%の食塩水が300g、容器㋑には8%の食塩水が600g入っています。
容器㋐と容器㋑から同じ重さの食塩水を取り出し、㋐から取り出した食塩水を㋑に、㋑から取り出した食塩水を㋐に入れて、それぞれかき混ぜました。
その結果、容器㋐の中の食塩水は6.2%になりました。
このとき、容器㋑の中の食塩水の濃さは何%になりましたか。
例題3
濃度が㋐%の食塩水が㋑g入っている容器に、濃度が1.9%の食塩水100gを加えて
よくかき混ぜると濃度が3.1%になりました。
そのあと食塩10gを加えてよくかき混ぜると、濃度が5%になりました。
㋐と㋑に当てはまる数字を答えなさい。
(2022年 灘中学校1日目 改題)
この動画を見る
例題1
2%の食塩水があります。
この食塩水を熱して240gの水を蒸発させると5%の食塩水ができます。
2%の食塩水は何gありますか。
例題2
容器㋐には5%の食塩水が300g、容器㋑には8%の食塩水が600g入っています。
容器㋐と容器㋑から同じ重さの食塩水を取り出し、㋐から取り出した食塩水を㋑に、㋑から取り出した食塩水を㋐に入れて、それぞれかき混ぜました。
その結果、容器㋐の中の食塩水は6.2%になりました。
このとき、容器㋑の中の食塩水の濃さは何%になりましたか。
例題3
濃度が㋐%の食塩水が㋑g入っている容器に、濃度が1.9%の食塩水100gを加えて
よくかき混ぜると濃度が3.1%になりました。
そのあと食塩10gを加えてよくかき混ぜると、濃度が5%になりました。
㋐と㋑に当てはまる数字を答えなさい。
(2022年 灘中学校1日目 改題)
ローソンのこれどっちがお得?

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ローソンの47%増量と値段が47%OFFだとどっちがお得なのか解説していきます。
この動画を見る
ローソンの47%増量と値段が47%OFFだとどっちがお得なのか解説していきます。
プレゼント企画何円かかった?

相当算(標準・発展)をサクッと学習しよう!【中学受験算数】【特殊算攻略講座8】

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
こばちゃん塾
問題文全文(内容文):
例題1
ある小学校の6年生の人数を調べると、
男子の人数は6年生全体の人数の 3分の1より20人多く、
女子の人数は6年生全体の人数の 2分の1より2人少ないことが 分かりました。
この学校の6年生は全部で 何人ですか。
例題2
たけしくんは、持っていたお金の6分の1と100円で本を買い、 次に残ったお金の1割と60円でノートを買ったところ、1200円が残りました。
たけしくんが買った本は何円でしたか。
例題3
ある本を、1日目は全体のページ数の4分の1を読み、2日目は残りの ページ数の5分の2を読み、3日目は215ページ読んだところ、まだあと172ページ残っていました。この本は全体で何ページありますか。
(豊島岡女子学園中学校)
この動画を見る
例題1
ある小学校の6年生の人数を調べると、
男子の人数は6年生全体の人数の 3分の1より20人多く、
女子の人数は6年生全体の人数の 2分の1より2人少ないことが 分かりました。
この学校の6年生は全部で 何人ですか。
例題2
たけしくんは、持っていたお金の6分の1と100円で本を買い、 次に残ったお金の1割と60円でノートを買ったところ、1200円が残りました。
たけしくんが買った本は何円でしたか。
例題3
ある本を、1日目は全体のページ数の4分の1を読み、2日目は残りの ページ数の5分の2を読み、3日目は215ページ読んだところ、まだあと172ページ残っていました。この本は全体で何ページありますか。
(豊島岡女子学園中学校)
大谷翔平の時給は?
2023年豊島岡女子学園中学校算数「売買損益」

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
【売買損益】
(1)仕入れ値を①とすると、5割増しの定価は、
定価:①$\times (1+$____)=〇
売り値は、定価の2割引きなので、
売り値:$○ \times(1-$____)=〇$\times$ ____=〇
「売り値-仕入れ値=利益」より
〇-〇=____円
〇=____円
仕入れ値①=____円$\div$____=____円
(2)定価は、仕入れ値120円の5割増しなので、
定価:____$\times (1+$____) = ____ $\times$ ____ = ____円
よって、定価で1個売れた場合の利益は、
____円 - ____円 = ____円なので、定価で____個売れた分の利益は、
____円$\times$____個=____円
全体の利益は、43,800円なので、2割引きの値段で売った分の利益は、
____ - ____ = ____円
定価____円の2割引きの売り値は、____円$\times(1-$____)= ____円$\times$____ = ____円
値引き価格で1個売れた場合の利益は、____円 - ____円 = ____円
よって、2割引きで売れた個数は、____ ÷ ____ = ____個
仕入れ数=定価で売れた分+値引き分=____個 + ____個 = ____個
この動画を見る
【売買損益】
(1)仕入れ値を①とすると、5割増しの定価は、
定価:①$\times (1+$____)=〇
売り値は、定価の2割引きなので、
売り値:$○ \times(1-$____)=〇$\times$ ____=〇
「売り値-仕入れ値=利益」より
〇-〇=____円
〇=____円
仕入れ値①=____円$\div$____=____円
(2)定価は、仕入れ値120円の5割増しなので、
定価:____$\times (1+$____) = ____ $\times$ ____ = ____円
よって、定価で1個売れた場合の利益は、
____円 - ____円 = ____円なので、定価で____個売れた分の利益は、
____円$\times$____個=____円
全体の利益は、43,800円なので、2割引きの値段で売った分の利益は、
____ - ____ = ____円
定価____円の2割引きの売り値は、____円$\times(1-$____)= ____円$\times$____ = ____円
値引き価格で1個売れた場合の利益は、____円 - ____円 = ____円
よって、2割引きで売れた個数は、____ ÷ ____ = ____個
仕入れ数=定価で売れた分+値引き分=____個 + ____個 = ____個
小5基礎トレ算数解説11/8⑥「食塩水濃度」
単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
重吉
問題文全文(内容文):
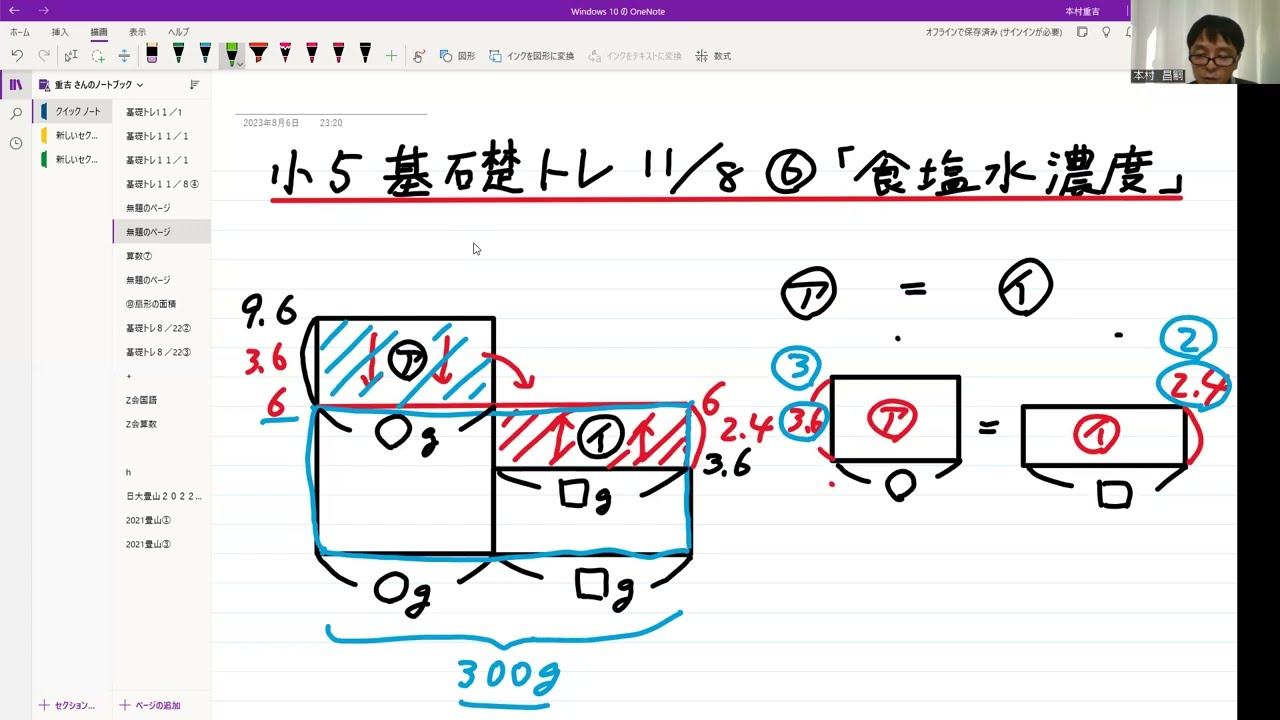
【食塩水濃度】
9.6%の食塩水が〇gあります
3.6%の食塩水が□gあります
合わせると合計300gあります
混ぜた後の食塩水は6.0%です
面積図を使用して、それぞれ最初に何gあったか求めよ
この動画を見る
【食塩水濃度】
9.6%の食塩水が〇gあります
3.6%の食塩水が□gあります
合わせると合計300gあります
混ぜた後の食塩水は6.0%です
面積図を使用して、それぞれ最初に何gあったか求めよ
小5基礎トレ解説11/1⑥「食塩水濃度」
単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
重吉
問題文全文(内容文):
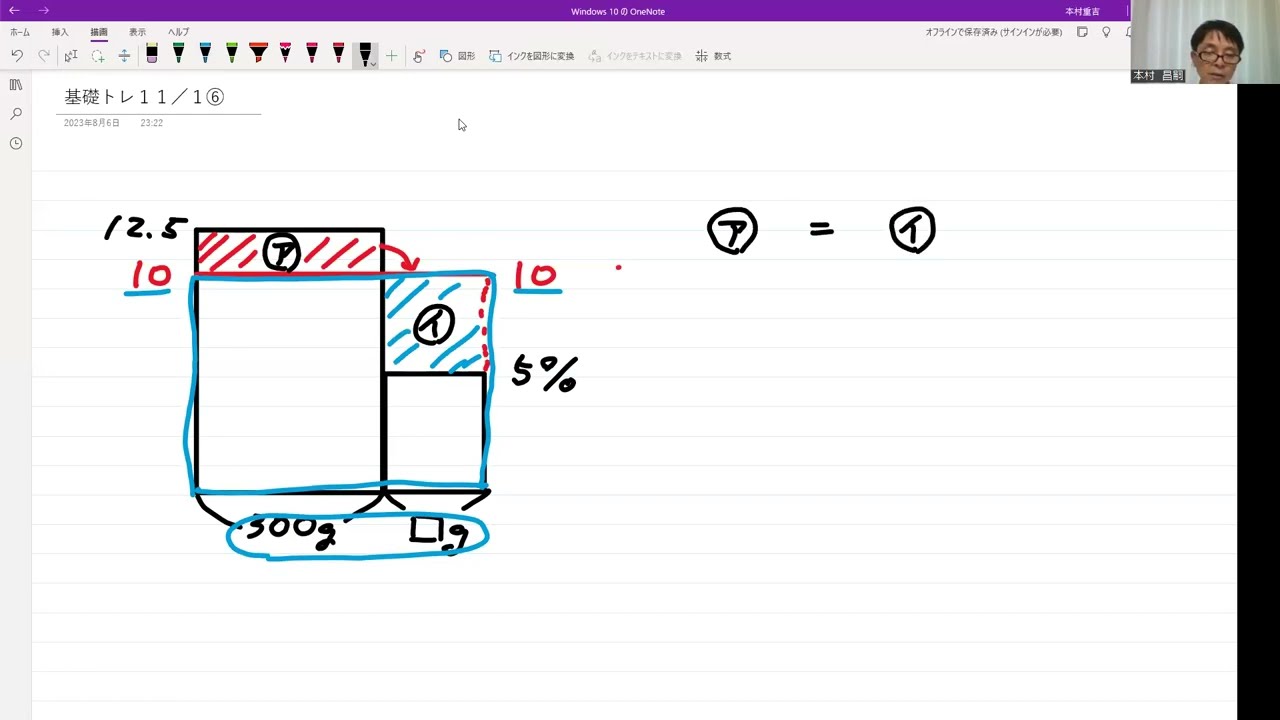
【食塩水濃度】
12.5%の食塩水300g、5%の食塩水□gがあり、これらを混ぜると10%の食塩水となります
□に入るg数を面積図を使って求めよ。
この動画を見る
【食塩水濃度】
12.5%の食塩水300g、5%の食塩水□gがあり、これらを混ぜると10%の食塩水となります
□に入るg数を面積図を使って求めよ。
飲み放題で元を取るには?
2023年栄東中学校算数「食塩水濃度」

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#栄東中学
指導講師:
重吉
問題文全文(内容文):
2023年栄東中学校算数「食塩水濃度」
5%の食塩水560gを作ろうと思ったが、量りが壊れており、水も食塩もそれぞれ□gずつお遅れてしまいました。
そのため、8%の食塩水になってしまった
余分な水と食塩は何gか求めよ。
この動画を見る
2023年栄東中学校算数「食塩水濃度」
5%の食塩水560gを作ろうと思ったが、量りが壊れており、水も食塩もそれぞれ□gずつお遅れてしまいました。
そのため、8%の食塩水になってしまった
余分な水と食塩は何gか求めよ。
【受験算数】神奈川大学附属2022B日程過去問売買損益

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#神奈川大学附属中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
りんご1個80円でいくつか仕入れ、3600円の利益を見込んで定価をつけて売り始めました。しかし、そのうちの10個が売れ残ったため、実際の利益は2400円となった。このとき定価は何円ですか。
この動画を見る
りんご1個80円でいくつか仕入れ、3600円の利益を見込んで定価をつけて売り始めました。しかし、そのうちの10個が売れ残ったため、実際の利益は2400円となった。このとき定価は何円ですか。
予習シリーズ算数6年上「ステップアップ演習」P108①(1)(2)
単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
重吉
問題文全文(内容文):
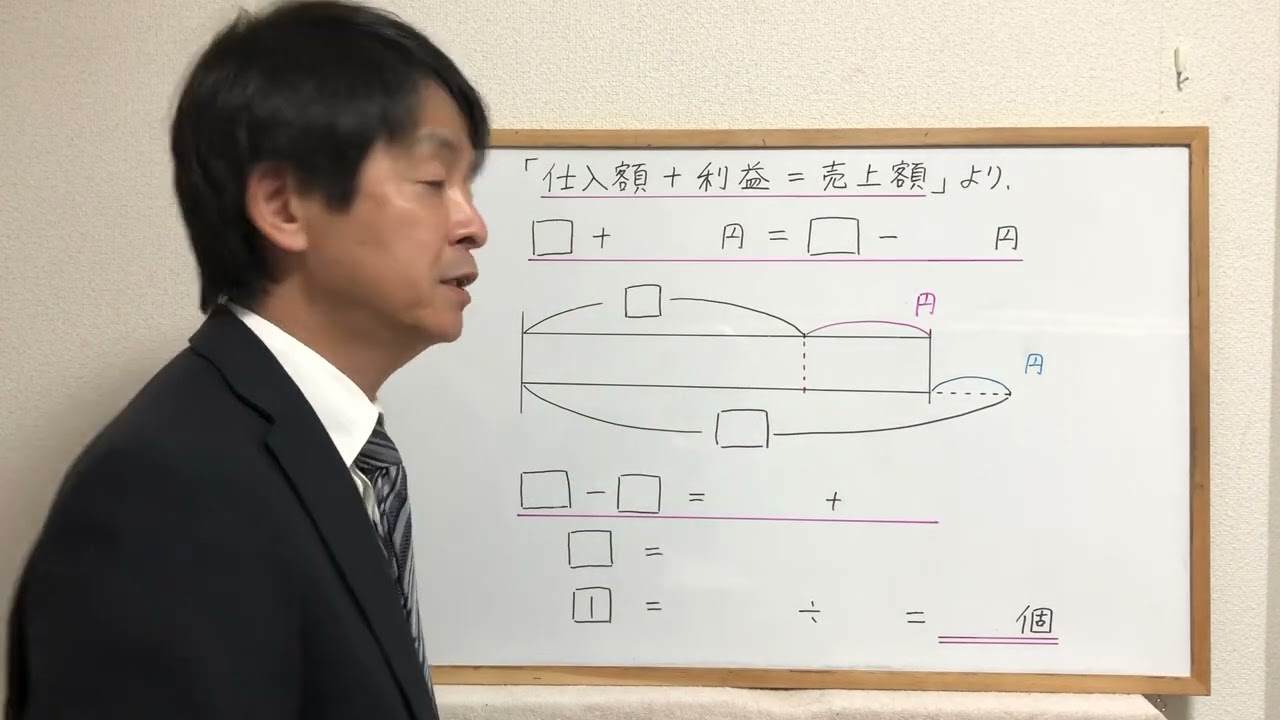
(1)仕入れ値に1割の利益を付けて販売し、利益が160円つきました。
仕入れ値がいくらか求めよ。
(2)リンゴの売上額を求めよ
また、リンゴの仕入れ個数を求めよ
この動画を見る
(1)仕入れ値に1割の利益を付けて販売し、利益が160円つきました。
仕入れ値がいくらか求めよ。
(2)リンゴの売上額を求めよ
また、リンゴの仕入れ個数を求めよ
2023年西大和学園中「食塩水濃度」解説

【題意から式を導く!】文章題:帝京高等学校~全国入試問題解法
単元:
#数学(中学生)#文章題#売買損益と食塩水#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
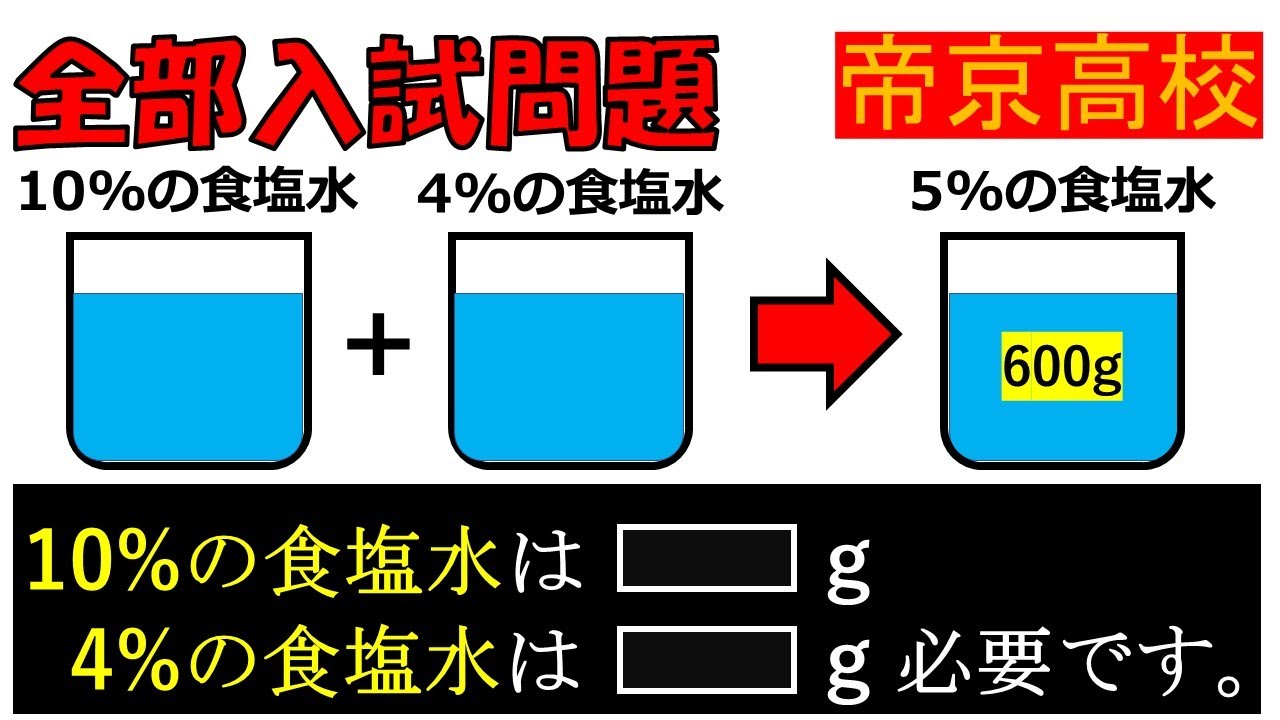
10%の食塩水と4%の食塩水を混ぜて5%の食塩水を600gつくるとき,
10%の食塩水と4%の食塩水はそれぞれ何g必要か?
帝京高等学校過去問
この動画を見る
10%の食塩水と4%の食塩水を混ぜて5%の食塩水を600gつくるとき,
10%の食塩水と4%の食塩水はそれぞれ何g必要か?
帝京高等学校過去問
100年継ぎ足したタレって残ってる?

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
100年継ぎ足したタレって100年前のタレどれくらい残ってるの?
この動画を見る
下記質問の解説動画です
100年継ぎ足したタレって100年前のタレどれくらい残ってるの?
【受験算数】食塩水を間違えて混ぜる問題もてんびんで一発!【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ算数・小5下#中学受験教材#濃さと比
指導講師:
理数個別チャンネル
問題文全文(内容文):
食塩水Aと、それより濃い食塩水Bがあります。AとBを、重さの比が3:1になるように混ぜる予定でしたが、まちがえて、重さの比を1:3にしてしまったので、できた食塩水と予定の食塩水の濃さの差は4%になりました。AとBの濃さの差は何%ですか。
この動画を見る
食塩水Aと、それより濃い食塩水Bがあります。AとBを、重さの比が3:1になるように混ぜる予定でしたが、まちがえて、重さの比を1:3にしてしまったので、できた食塩水と予定の食塩水の濃さの差は4%になりました。AとBの濃さの差は何%ですか。
【受験算数】食塩水の混ぜた重さの比もてんびんで即答!【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ算数・小5下#中学受験教材#濃さと比
指導講師:
理数個別チャンネル
問題文全文(内容文):
5%の食塩水と13%の食塩水を混ぜたところ、8%の食塩水になりました。5%の食塩水と13%の食塩水の混ぜた重さの比を求めなさい。
この動画を見る
5%の食塩水と13%の食塩水を混ぜたところ、8%の食塩水になりました。5%の食塩水と13%の食塩水の混ぜた重さの比を求めなさい。
スシローが1億円利益出すには?

単元:
#算数(中学受験)#売買損益と食塩水
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
スシローが1億円利益出すにはどうしたらいいですか?
この動画を見る
下記質問の解説動画です
スシローが1億円利益出すにはどうしたらいいですか?
【基本を守ってすんなり解答!】文章題:久留米大附設高等学校~全国入試問題解法
単元:
#数学(中学生)#文章題#売買損益と食塩水#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
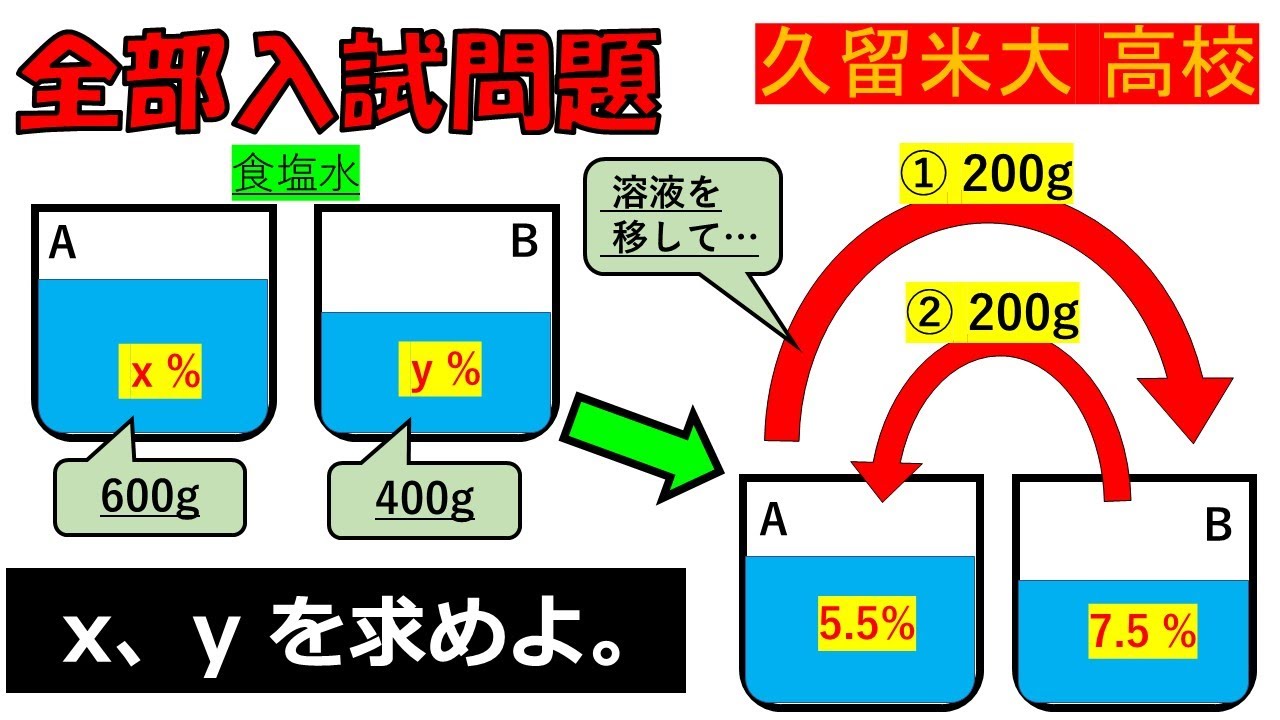
Aから食塩水を200g取り出してBに入れ,よくかき混ぜた後にBから200g取り出して
Aに戻す操作を行うとAの濃度は5.5%,Bの濃度は7.5%になった.
x,yをそれぞれ求めよ.
久留米大附設高等学校過去問
この動画を見る
Aから食塩水を200g取り出してBに入れ,よくかき混ぜた後にBから200g取り出して
Aに戻す操作を行うとAの濃度は5.5%,Bの濃度は7.5%になった.
x,yをそれぞれ求めよ.
久留米大附設高等学校過去問
2023高校入試解説3問目 食塩水 方程式立てずに溶ける!! 等濃度 等量交換 早稲田佐賀

単元:
#数学(中学生)#文章題#売買損益と食塩水#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
食塩水A:5% 80g
食塩水B:7% 120g
食塩水AとBから同量取り出し、A→B、B→Aへ入れるとA,Bの食塩水の濃度が等しくなった。
取り出した食塩水の量は?
2023早稲田佐賀高等学校
この動画を見る
食塩水A:5% 80g
食塩水B:7% 120g
食塩水AとBから同量取り出し、A→B、B→Aへ入れるとA,Bの食塩水の濃度が等しくなった。
取り出した食塩水の量は?
2023早稲田佐賀高等学校
【直前にもう一度見なおしたい!】文章題:専修大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#文章題#売買損益と食塩水#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
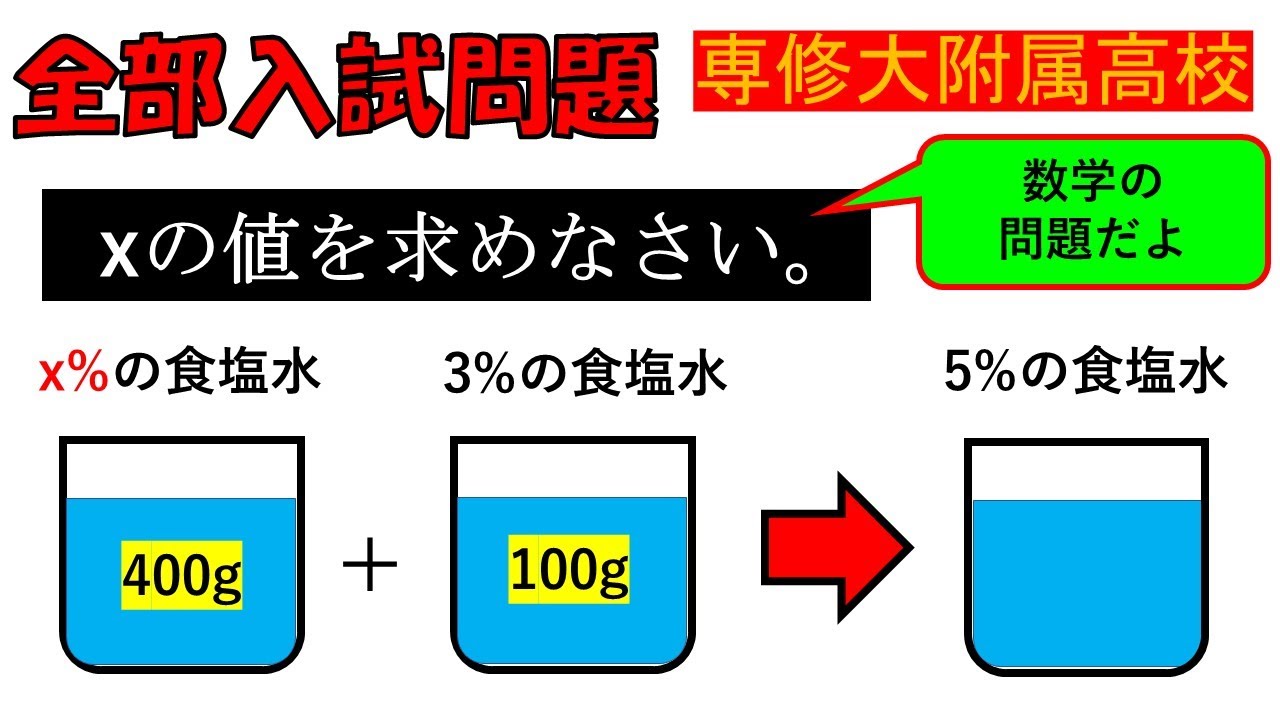
$A$の容器に$x$%の食塩水が400g入っている.
$A$の容器に$3$%の食塩水を100g加え,よくかき混ぜたところ,
$A$の容器の食塩水は$5$%となった.
$x$の値を求めなさい.
専修大学附属高等学校過去問
この動画を見る
$A$の容器に$x$%の食塩水が400g入っている.
$A$の容器に$3$%の食塩水を100g加え,よくかき混ぜたところ,
$A$の容器の食塩水は$5$%となった.
$x$の値を求めなさい.
専修大学附属高等学校過去問
音楽を聴きながら、マジで濃度計算が得意になる動画~全国入試問題解法 #shorts #数学 #理科

単元:
#数学(中学生)#文章題#売買損益と食塩水#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
300gの水が入った容器の10%が食塩水である.
では,4.8%の食塩水が入ったときの食塩水と水は$\Box$か.
$\Box$を求めよ.
日大習志野高校過去問
この動画を見る
300gの水が入った容器の10%が食塩水である.
では,4.8%の食塩水が入ったときの食塩水と水は$\Box$か.
$\Box$を求めよ.
日大習志野高校過去問
1円作るだけでどれだけ損してきたのか?

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
お金作るのにそれ以上のお金使うって言いますが、日本はどれくらい損していますか?
この動画を見る
下記質問の解説動画です
お金作るのにそれ以上のお金使うって言いますが、日本はどれくらい損していますか?
カルピスウォーターと原液どっちが得?

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
カルピスウォーターとカルピス原液のどっちがお得ですか?
この動画を見る
下記質問の解説動画です
カルピスウォーターとカルピス原液のどっちがお得ですか?
