資料の活用
資料の活用
【中学数学】箱ひげ図データの分析～2022年度北海道公立高校入試～【高校受験】
単元：
#数学(中学生)#中１数学#資料の活用#高校入試過去問(数学)#北海道公立高校入試
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
北海道公立高校2022年数学過去問
春奈さんたちの中学校では, 3年生のA組30人全員と, B組30人全員の50m走の記録を調査 しました。 次の問いに答えなさい。
問1 図1は, A組, B組全員の記録を、 それぞれ箱ひげ図にまとめたものです。（図は動画内参照）
次の(1),(2) に答えなさい。
(1) B組の記録の第3四分位数を求めなさい
(2) データの散らばり (分布) の程度について、 図1から読みとれることとして
最も適当なものを、次のア~エから1つ選びなさい
ア範囲は, A組の方がB組よりも小さい。
イ四分位範囲は, A組の方がB組よりも大きい。
ウ平均値は, A組の方がB組よりも小さい。
エ最大値は, A組の方がB組よりも大きい。
この動画を見る
北海道公立高校2022年数学過去問
春奈さんたちの中学校では, 3年生のA組30人全員と, B組30人全員の50m走の記録を調査 しました。 次の問いに答えなさい。
問1 図1は, A組, B組全員の記録を、 それぞれ箱ひげ図にまとめたものです。（図は動画内参照）
次の(1),(2) に答えなさい。
(1) B組の記録の第3四分位数を求めなさい
(2) データの散らばり (分布) の程度について、 図1から読みとれることとして
最も適当なものを、次のア~エから1つ選びなさい
ア範囲は, A組の方がB組よりも小さい。
イ四分位範囲は, A組の方がB組よりも大きい。
ウ平均値は, A組の方がB組よりも小さい。
エ最大値は, A組の方がB組よりも大きい。
【中学数学】数学用語チェック絵本 中2の用語”せめて”これだけは覚えよう！！act2まとめ
単元：
#数学(中学生)#中１数学#中２数学#式の計算（単項式・多項式・式の四則計算）#連立方程式#資料の活用#1次関数#平行と合同#確率#三角形と四角形
指導講師：
理数個別チャンネル
問題文全文(内容文)：
中２で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ！act2vol.1～7の方も見てね♪
この動画を見る
中２で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ！act2vol.1～7の方も見てね♪
【中学数学】数学用語チェック絵本 act2 vol.7 データの比較
【中学数学】数学用語チェック絵本 中1の用語”せめて”これだけは覚えよう！！
単元：
#数学(中学生)#中１数学#正の数・負の数#方程式#比例・反比例#空間図形#資料の活用#文字と式#平面図形
指導講師：
理数個別チャンネル
問題文全文(内容文)：
中１で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ！vol.1～7の方も見てね♪
この動画を見る
中１で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ！vol.1～7の方も見てね♪
【中学数学】数学用語チェック絵本 vol.7 データの分析と活用
【数検3級】中学数学：数学検定3級2次：問題9
単元：
#数学(中学生)#中１数学#数学検定・数学甲子園・数学オリンピック等#資料の活用#数学検定#数学検定3級
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問題9.次の問いに答えなさい。
(19) ある中学校の1年生の生徒数は18人、2年生の生徒数は27人、3年生の生徒数は20人です。それぞれの学年の通学時間を調べて平均を求めると、１年生は15.5分、2年生は32.0分、3年生は21.5分でした。生徒全体の通学時間の平均は何分ですか。
(20) いくつかの値からなるデータの中に極端にかけ離れた値があると、平均値はその値に強く影響を受けてしまうことがあります。
Ａさんは5つの正の整数を思い浮かべました。これらの数の平均値は2021です。このとき、Ａさんが思い浮かべた可能性がある数
の最大値を求めなさい。ただし、5つの数に同じ数があってもよいものとします。
この動画を見る
問題9.次の問いに答えなさい。
(19) ある中学校の1年生の生徒数は18人、2年生の生徒数は27人、3年生の生徒数は20人です。それぞれの学年の通学時間を調べて平均を求めると、１年生は15.5分、2年生は32.0分、3年生は21.5分でした。生徒全体の通学時間の平均は何分ですか。
(20) いくつかの値からなるデータの中に極端にかけ離れた値があると、平均値はその値に強く影響を受けてしまうことがあります。
Ａさんは5つの正の整数を思い浮かべました。これらの数の平均値は2021です。このとき、Ａさんが思い浮かべた可能性がある数
の最大値を求めなさい。ただし、5つの数に同じ数があってもよいものとします。
ここ分からんかったやろ？
単元：
#数学(中学生)#中１数学#数Ⅰ#資料の活用#データの分析#データの分析#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
四分位数
四分位範囲
箱ひげ図
解説動画です
この動画を見る
四分位数
四分位範囲
箱ひげ図
解説動画です
【中学数学】平均値～度数分布表から求める方法～【中１数学】
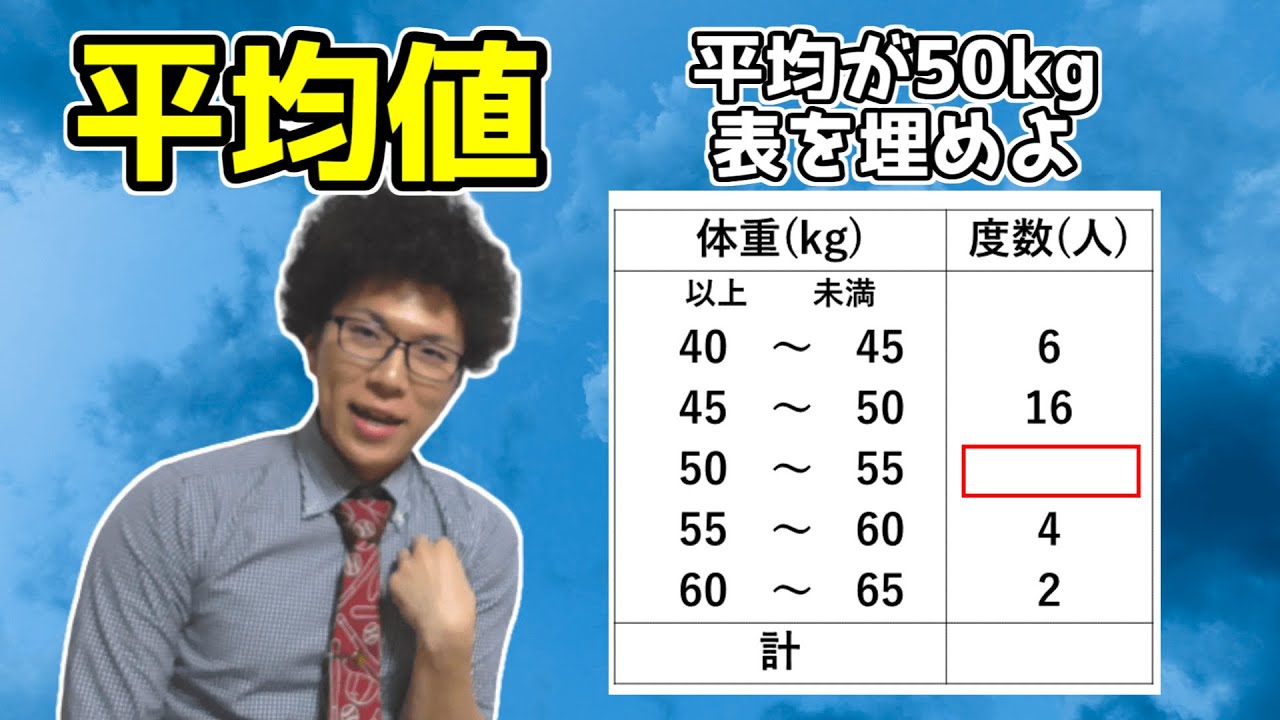
中１数学「範囲と平均値」【毎日配信】
単元：
#数学(中学生)#中１数学#資料の活用
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第68回範囲と平均値~
例1
8人の生徒に10点満点の英単語テストを実施したら、 以下のようになりました。
10点、8点、7点7点,8点10点3点7点,
(1)この資料の範囲を求めなさい。
(2)平均値を求めなさい。
例2
次の図はあるクラスの男子20人の体重をヒストグラムで 表したものです。クラスの体重の平均値を求めなさい。
この動画を見る
中1~第68回範囲と平均値~
例1
8人の生徒に10点満点の英単語テストを実施したら、 以下のようになりました。
10点、8点、7点7点,8点10点3点7点,
(1)この資料の範囲を求めなさい。
(2)平均値を求めなさい。
例2
次の図はあるクラスの男子20人の体重をヒストグラムで 表したものです。クラスの体重の平均値を求めなさい。
【中学数学】相対度数をどこよりも丁寧に【中１数学】
【中学数学】ヒストグラム・度数折れ線を超丁寧に【中１数学】
【中学数学】度数分布表や用語の確認～資料・データの整理～【中１数学】
【高校受験対策/数学】死守82
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#平方根#資料の活用#1次関数#文字と式#平面図形#標本調査
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守82
①$3-(-6)$を計算しなさい。
②$9÷(-\frac{1}{5})+4$を計算しなさい。
③$\sqrt{28}-\sqrt{7}$を計算しなさい。
④下の図のように、半径が$9cm$、中心角が$60°$のおうぎ形$OAB$があります。
このおうぎ形の弧$AB$の長さを求めなさい。
ただし円周率は$\pi$を用いなさい。
⑤右の表は、A中学校の3年生男子80人の立ち幅とびの記録を度数分布表にまと めたものです。
度数が最も多い階級の相対度数を求めなさい。
⑥関数$y=3x$のグラフに平行で、 点$(0,2)$を通る直線の式を求めなさい。
⑦右の図の四角形$ABCD$において、点$B$と点$Dが$重なるように折ったときにできる折り目の線と
辺$AB$、$BC$との交点をそれぞれ$P,Q$とします。
2点$P,Q$を定規とコンパスを使って作図しなさい。
ただし、点を示す記号$P,Q$をかき入れ、作図に用いた線は消さないこと。
この動画を見る
高校受験対策・死守82
①$3-(-6)$を計算しなさい。
②$9÷(-\frac{1}{5})+4$を計算しなさい。
③$\sqrt{28}-\sqrt{7}$を計算しなさい。
④下の図のように、半径が$9cm$、中心角が$60°$のおうぎ形$OAB$があります。
このおうぎ形の弧$AB$の長さを求めなさい。
ただし円周率は$\pi$を用いなさい。
⑤右の表は、A中学校の3年生男子80人の立ち幅とびの記録を度数分布表にまと めたものです。
度数が最も多い階級の相対度数を求めなさい。
⑥関数$y=3x$のグラフに平行で、 点$(0,2)$を通る直線の式を求めなさい。
⑦右の図の四角形$ABCD$において、点$B$と点$Dが$重なるように折ったときにできる折り目の線と
辺$AB$、$BC$との交点をそれぞれ$P,Q$とします。
2点$P,Q$を定規とコンパスを使って作図しなさい。
ただし、点を示す記号$P,Q$をかき入れ、作図に用いた線は消さないこと。
【中学数学】四分位範囲と箱ひげ図が誰でも分かるようになる授業動画【中２数学】
【数学】中2-88 箱ひげ図②(読み取り編)
単元：
#数学(中学生)#中１数学#資料の活用
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数学(箱ひげ図②・読み取り編)
Q.
右の2つの箱ひげ図は、Aグループ15人とBグループ15人のテストの得点を表したものです。
この箱ひげ図から読み取れることとして、次の①~④は正しいといえますか。
「正しい」「正しくない」「このデータからはわからない」のどれかで答えなさい。
①Bグループの平均値は6点である。
②どちらのグループも、半分以上の生徒が5点以上である。
③Aグループは7点以上の人が4人いる。
④範囲も四分位範囲もBグループの方が大きい。
この動画を見る
数学(箱ひげ図②・読み取り編)
Q.
右の2つの箱ひげ図は、Aグループ15人とBグループ15人のテストの得点を表したものです。
この箱ひげ図から読み取れることとして、次の①~④は正しいといえますか。
「正しい」「正しくない」「このデータからはわからない」のどれかで答えなさい。
①Bグループの平均値は6点である。
②どちらのグループも、半分以上の生徒が5点以上である。
③Aグループは7点以上の人が4人いる。
④範囲も四分位範囲もBグループの方が大きい。
【数学】中2-87 箱ひげ図①(基本編)
単元：
#数学(中学生)#中１数学#資料の活用
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
数学(箱ひげ図①・基本編)
Q.
下の資料は、とある生徒9人が行った小テストの得点である。
7 5 4 9 6 7 10 3 6
①最小値は？
➁最大値は？
③第１四分位数は？
④第２四分位数は？
⑤第３四分位数は？
⑥範囲は？
⑦四分位範囲は？
⑧箱ひげ図に表しなさい。
この動画を見る
数学(箱ひげ図①・基本編)
Q.
下の資料は、とある生徒9人が行った小テストの得点である。
7 5 4 9 6 7 10 3 6
①最小値は？
➁最大値は？
③第１四分位数は？
④第２四分位数は？
⑤第３四分位数は？
⑥範囲は？
⑦四分位範囲は？
⑧箱ひげ図に表しなさい。
中１数学「最頻値と中央値」【毎日配信】
単元：
#数学(中学生)#中１数学#資料の活用
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第69回最頻値と中央値~
例1
8人の生徒に10点満点の英単語テストを実施したら、 以下のようになりました。
10点8点7点7点,8点,10点、3点、7点
(1)最頻値を求めなさい。
(2) 中央値を求めなさい。
例2
次の図はあるクラスの男子20人の体重をヒストグラムで 表したものです。
(1)最頻値を求めなさい。
(2) 中央値の含まれる階段を答えなさい。
この動画を見る
中1~第69回最頻値と中央値~
例1
8人の生徒に10点満点の英単語テストを実施したら、 以下のようになりました。
10点8点7点7点,8点,10点、3点、7点
(1)最頻値を求めなさい。
(2) 中央値を求めなさい。
例2
次の図はあるクラスの男子20人の体重をヒストグラムで 表したものです。
(1)最頻値を求めなさい。
(2) 中央値の含まれる階段を答えなさい。
中１数学「度数分布多角形（度数折れ線）」【毎日配信】
単元：
#数学(中学生)#中１数学#資料の活用
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第67回度数分布多角形~
例題
次の図はあるクラス24人の英語と数学のテスト結果を 度数分布多角形で表したものです。
次の階級の相対度数を小教第2位までで求めなさい。
(1)英語60点以上80点未満
(2)数学20点以上40点未満
この動画を見る
中1~第67回度数分布多角形~
例題
次の図はあるクラス24人の英語と数学のテスト結果を 度数分布多角形で表したものです。
次の階級の相対度数を小教第2位までで求めなさい。
(1)英語60点以上80点未満
(2)数学20点以上40点未満
中１数学「ヒストグラム（柱状グラフ）」【毎日配信】
単元：
#数学(中学生)#中１数学#資料の活用
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第66回ヒストグラム~
例題
次の表は、ある中学校のクラスの体重を、ヒストグラムで 表したものです。
(1)階級の幅は何kgですか。
(2) 50kgの生徒は、重い方から数えて 何番目から何番目の間にいますか。
(3) 48kg以上52kg未満の相対度数を 求めなさい。
(4) 40kg未満の相対度数を求めなさい。
この動画を見る
中1~第66回ヒストグラム~
例題
次の表は、ある中学校のクラスの体重を、ヒストグラムで 表したものです。
(1)階級の幅は何kgですか。
(2) 50kgの生徒は、重い方から数えて 何番目から何番目の間にいますか。
(3) 48kg以上52kg未満の相対度数を 求めなさい。
(4) 40kg未満の相対度数を求めなさい。
中１数学「度数分布表と相対度数」【毎日配信】
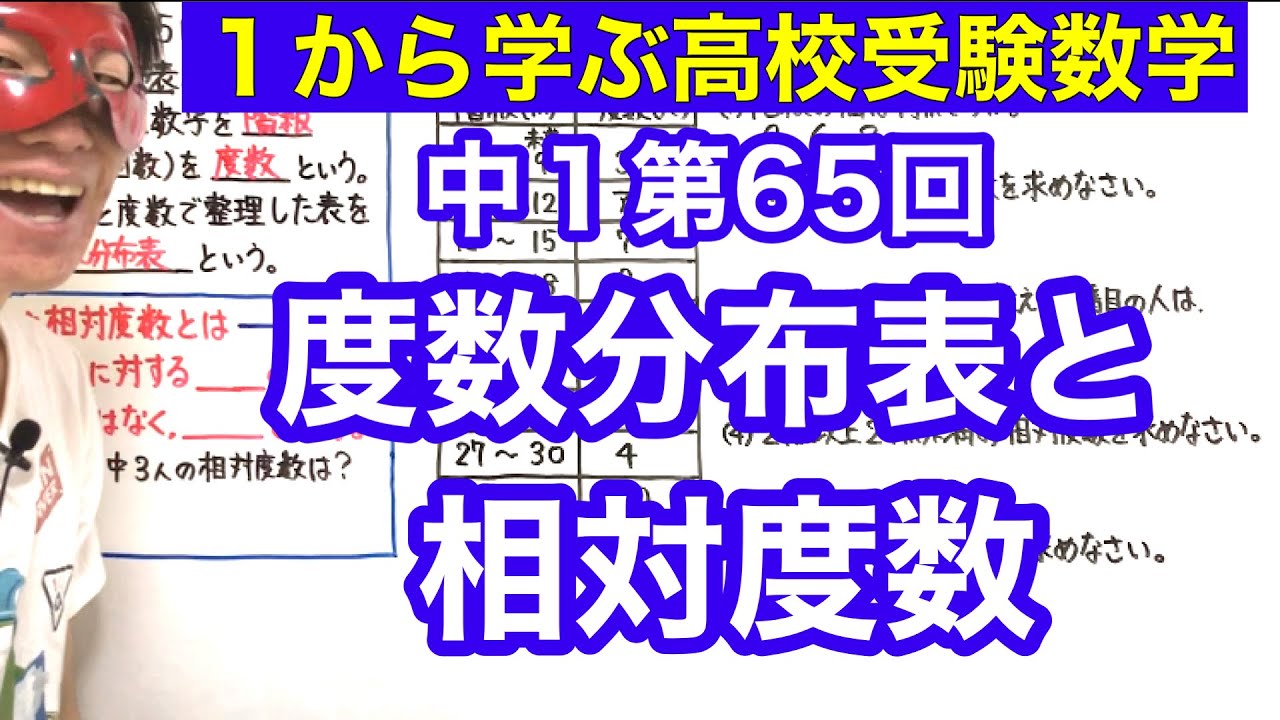
単元：
#数学(中学生)#中１数学#資料の活用
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第65回度数分布表と相対度数~
例題
次の表は、ある中学校50人のハンドボール投げの 記録を度数分布表に整理したものです。
(1) 階級の幅は何mですか。
(2)表のアにあてはまる数を求めなさい。
(3) 記録がよくない方から数えて8番目の人は。 どの階級に入りますか。
(4)21m以上24m未満の相対度数を求めなさい。
(5) 15m未満の相対度数を求めなさい。
この動画を見る
中1~第65回度数分布表と相対度数~
例題
次の表は、ある中学校50人のハンドボール投げの 記録を度数分布表に整理したものです。
(1) 階級の幅は何mですか。
(2)表のアにあてはまる数を求めなさい。
(3) 記録がよくない方から数えて8番目の人は。 どの階級に入りますか。
(4)21m以上24m未満の相対度数を求めなさい。
(5) 15m未満の相対度数を求めなさい。
【算数・中学数学・数Ⅰ】算数でも数学でも出てくる「平均値と中央値」の違い～年収のお話もあるよ～ ※2020年度学習指導要領改訂で中央値は算数で習うようになりました。
単元：
#算数(中学受験)#数学(中学生)#中１数学#数Ⅰ#資料の活用#データの分析#データの分析#その他#その他#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
平均と中央値って何が違うの？？日本の平均年収441万円ってどうなのよ？？
データを読み解く力は、今後とても大切です！！必見。
この動画を見る
平均と中央値って何が違うの？？日本の平均年収441万円ってどうなのよ？？
データを読み解く力は、今後とても大切です！！必見。
【高校受験対策/数学】死守56
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#式の計算（単項式・多項式・式の四則計算）#平方根#比例・反比例#資料の活用#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守56
①$4-6 \div (-2)$を計算しなさい。
②$(\sqrt{5}-1)^2+\sqrt{20}$を計算しなさい。
③$(2x+1)(3x-1)-(2x-1)(3x+1)$を計算しなさい。
④方程式$(x+1)(x-1) = 3(x+1)$を解きなさい。
⑤500円出して$a$円の鉛筆5本と $b$円の消しゴム1個を買うと、おつりがあった。
この数量の関係を不等式で表しなさい。
⑥2種類の体験学習A・Bがあり、生徒は必ずA・Bのいずれか一方に参加する。
A・Bそれぞれを希望する生徒の人数の比は$1:2$であった。
その後、14人の生徒がBからAへ希望を変更したため、A.Bそれぞれを希望する生徒の人数の比は$5:7$となった。
体験学習に参加する生徒の人数は何人か、求めなさい。
⑦関数に$y=x^2$について正しく述べたものを、次のア~エからすべて選びなさい。
ア $x$の値が増加すると、$y$の値も増加する。
イ グラフが$y$軸を対称の軸として線対称である。
ウ $x$の変域が$-1 \leqq x \leqq 2$のとき、その変域は$-1 \leqq y \leqq 4$
である。
エ $x$がどんな値をとっても、$y \geqq 0$である。
⑧男子生徒6人のハンドボール投げの記録は右のようであった。
6人のハンドボール投げの記録の中央値は何mか求めなさい。
この動画を見る
高校受験対策・死守56
①$4-6 \div (-2)$を計算しなさい。
②$(\sqrt{5}-1)^2+\sqrt{20}$を計算しなさい。
③$(2x+1)(3x-1)-(2x-1)(3x+1)$を計算しなさい。
④方程式$(x+1)(x-1) = 3(x+1)$を解きなさい。
⑤500円出して$a$円の鉛筆5本と $b$円の消しゴム1個を買うと、おつりがあった。
この数量の関係を不等式で表しなさい。
⑥2種類の体験学習A・Bがあり、生徒は必ずA・Bのいずれか一方に参加する。
A・Bそれぞれを希望する生徒の人数の比は$1:2$であった。
その後、14人の生徒がBからAへ希望を変更したため、A.Bそれぞれを希望する生徒の人数の比は$5:7$となった。
体験学習に参加する生徒の人数は何人か、求めなさい。
⑦関数に$y=x^2$について正しく述べたものを、次のア~エからすべて選びなさい。
ア $x$の値が増加すると、$y$の値も増加する。
イ グラフが$y$軸を対称の軸として線対称である。
ウ $x$の変域が$-1 \leqq x \leqq 2$のとき、その変域は$-1 \leqq y \leqq 4$
である。
エ $x$がどんな値をとっても、$y \geqq 0$である。
⑧男子生徒6人のハンドボール投げの記録は右のようであった。
6人のハンドボール投げの記録の中央値は何mか求めなさい。
中学１年生で勉強する資料の分析を１本の動画にまとめてみました【新学習指導要領】
単元：
#数学(中学生)#中１数学#資料の活用
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
資料の分析と活用のまとめ
右の表1を(①)表という。 ※表は動画参照
資料を整理するために用いる区間を(②)
区間の幅を(③)、(➁)の真ん中の値を(④)、その(➁)に入っている資料の個数を(⑤)といい
その(➁)に入っている資料の個数を(⑤)といい、(⑤)の合計に対する割合を(⑥)という。
また、表2のような柱状グラフを(⑦)といい、
それぞれの長方形の上の辺の中点を結んだものを(⑧)線という。
この動画を見る
資料の分析と活用のまとめ
右の表1を(①)表という。 ※表は動画参照
資料を整理するために用いる区間を(②)
区間の幅を(③)、(➁)の真ん中の値を(④)、その(➁)に入っている資料の個数を(⑤)といい
その(➁)に入っている資料の個数を(⑤)といい、(⑤)の合計に対する割合を(⑥)という。
また、表2のような柱状グラフを(⑦)といい、
それぞれの長方形の上の辺の中点を結んだものを(⑧)線という。
【中1 数学】中1-88 近似値
単元：
#数学(中学生)#中１数学#資料の活用
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①～⑪を求めよ。
◎有効数字と有効数字のけた数は?
①$5,2 \times 10^3$
②$7,25 \times 10^4$
③$1,90 \times 10^3$
◎次の測定値を有効数字$3$けたで表すと?
④$2843m$
⑤$34570g$
⑥$82951730km$
◎次の測定値は何の位まで測定したもの
⑦$9,24 \times 10^2g$
⑧$1,40 \times 10^3m$
◎真の値$125,6㎡$を$124,8㎡$と測定しました。
⑨このときの誤差は?
◎ある数の$a$を()の位で四捨五入して近似値をだしました。
$a$の範囲を不等号を使って書こう!!
⑩$329$(小数第$1$位)
⑪$5、6$(小数第$2$位)
この動画を見る
①～⑪を求めよ。
◎有効数字と有効数字のけた数は?
①$5,2 \times 10^3$
②$7,25 \times 10^4$
③$1,90 \times 10^3$
◎次の測定値を有効数字$3$けたで表すと?
④$2843m$
⑤$34570g$
⑥$82951730km$
◎次の測定値は何の位まで測定したもの
⑦$9,24 \times 10^2g$
⑧$1,40 \times 10^3m$
◎真の値$125,6㎡$を$124,8㎡$と測定しました。
⑨このときの誤差は?
◎ある数の$a$を()の位で四捨五入して近似値をだしました。
$a$の範囲を不等号を使って書こう!!
⑩$329$(小数第$1$位)
⑪$5、6$(小数第$2$位)
【中1 数学】中1-87 代表値と散らばり
単元：
#数学(中学生)#中１数学#資料の活用
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①～⑬の空欄を埋めよ。
◎英単語10問テストをやりました!!
男6,7,9,10,8,3,5,8,6,4,10,2,5,8
女
【男子について…】
⑤平均値は?
⑥最頻値は?
⑦中央値は?
⑧得点の範囲は?
【女子について…】
⑨平均値は?
⑩最頻値は?
最頻値は⑪＿＿＿＿、中央値は⑫＿＿＿＿
範囲は⑬＿＿＿＿ともいうんだ!!
※表は動画内参照
この動画を見る
①～⑬の空欄を埋めよ。
◎英単語10問テストをやりました!!
男6,7,9,10,8,3,5,8,6,4,10,2,5,8
女
【男子について…】
⑤平均値は?
⑥最頻値は?
⑦中央値は?
⑧得点の範囲は?
【女子について…】
⑨平均値は?
⑩最頻値は?
最頻値は⑪＿＿＿＿、中央値は⑫＿＿＿＿
範囲は⑬＿＿＿＿ともいうんだ!!
※表は動画内参照
【中1 数学】中1-86 度数分布
単元：
#数学(中学生)#中１数学#資料の活用
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎①～⑫をうめて度数分布表を完成させよう!!
⑬度数がもっとも多い階級は?
⑭身長が140cm以上160cm未満の人数は 全体の何%ですか?
⑮右下にヒストグラムを書こう!
⑯右下に 度数分布多角形を書こう!!
※表は動画内参照
この動画を見る
◎①～⑫をうめて度数分布表を完成させよう!!
⑬度数がもっとも多い階級は?
⑭身長が140cm以上160cm未満の人数は 全体の何%ですか?
⑮右下にヒストグラムを書こう!
⑯右下に 度数分布多角形を書こう!!
※表は動画内参照