【中学数学】図形を折る問題の基礎～長野県2022年度公立高校入試～【高校受験】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中１数学 > 平面図形 > 【中学数学】図形を折る問題の基礎～長野県2022年度公立高校入試～【高校受験】

【中学数学】図形を折る問題の基礎～長野県2022年度公立高校入試～【高校受験】

問題文全文(内容文)：
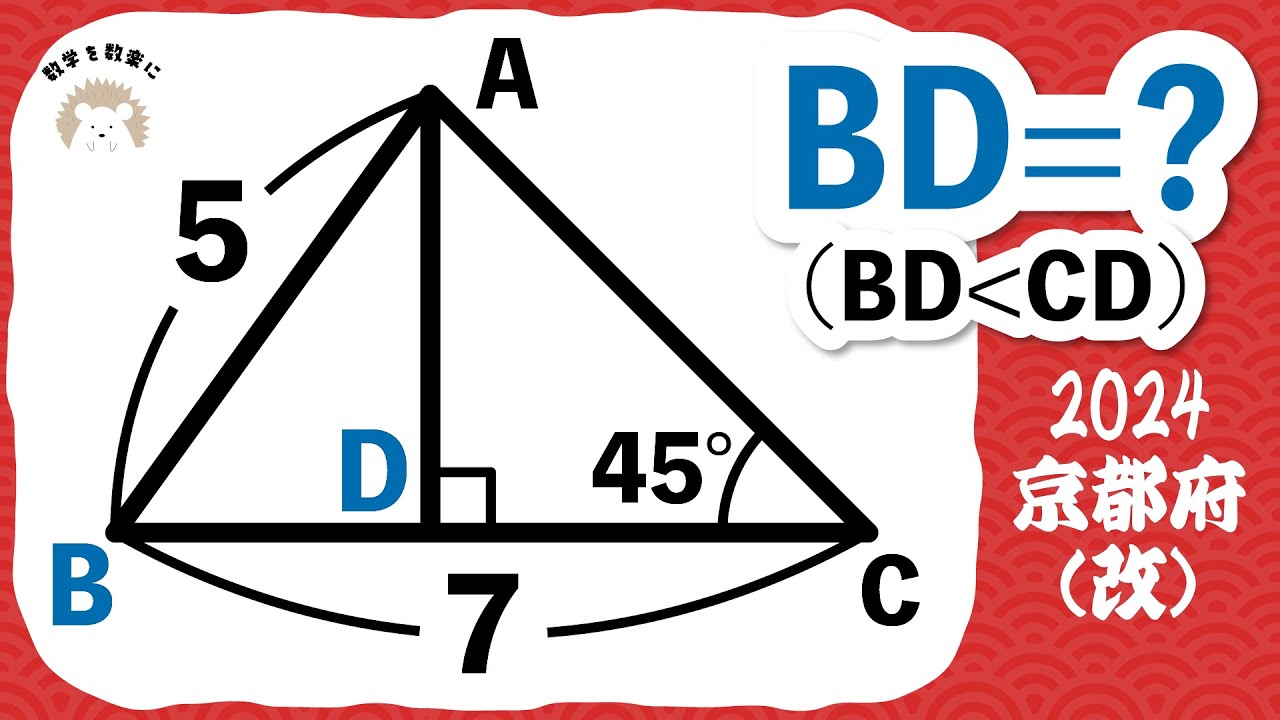
1辺の長さが6cmの正三角形ABCがある。
図は正三角形ABCを頂点Aが頂点Cに重なるように折り曲げたとき、折り目の線分をBDとしたものである。
このとき、BDの長さを求めよ。

※図は動画内参照
単元： #数学(中学生)#中１数学#平面図形
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1辺の長さが6cmの正三角形ABCがある。
図は正三角形ABCを頂点Aが頂点Cに重なるように折り曲げたとき、折り目の線分をBDとしたものである。
このとき、BDの長さを求めよ。

※図は動画内参照
投稿日：2023.01.22

＜関連動画＞

【中1数学】元大手塾講師が教える！中学数学基礎講座　第１４回　文字式の表し方

アイキャッチ画像
単元： #数学(中学生)#中１数学#文字と式
指導講師： こばちゃん塾
問題文全文(内容文)：
例題
(1)b×4×a
(2)m×m×3
(3)(a+b)÷2


例題
(1)1000円を出して、1個x円のボールを2個買ったときのおつり
(2)時速ykmで3時間走ったときの道のり
(3)全校生徒a人の11%の人数


1本a円のばらと1本b円のゆりがあります。
a+3b(円)は何を表していますか。
この動画を見る　

中１数学「四則混合計算②（分配法則）」【毎日配信】

アイキャッチ画像
単元： #数学(中学生)#中１数学#正の数・負の数
指導講師： 中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
四則混合計算②（分配法則)に関して解説していきます。
この動画を見る　

数学の文章題を解く流れをつかむ30秒～全国入試問題解法 #shorts #数学 #高校受験 #mathematics

アイキャッチ画像
単元： #数学(中学生)#中１数学#文字と式#高校入試過去問(数学)#精華女子高等学校
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
ある自然数を2乗して3引くところを間違えて2倍して3引いたので,
正しい答えより15小さくなった.ある自然数を求めよ.

精華女子高校過去問
この動画を見る　

【そして経験したことを思い出して】図形：国立高等専門学校～全国入試問題解法

アイキャッチ画像
単元： #数学(中学生)#中１数学#角度と面積#平面図形#高校入試過去問(数学)
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \angle x$は$\Box$である.
この動画を見る　

【中１　数学】　１－１０（旧）　文字を使うルール

アイキャッチ画像
単元： #数学(中学生)#中１数学#文字と式
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
中1 数学　文字を使うルール（文字式の表し方）
●（$\times$）のルール
①アルファベットの順番。
②教字が先。
③同じものは‥。
④1は書かない。
⑤（　）はうしろ。

●（$\div$）のルール
①分数にしちゃいなよ。
②（　）はセットで。
この動画を見る　
PAGE TOP