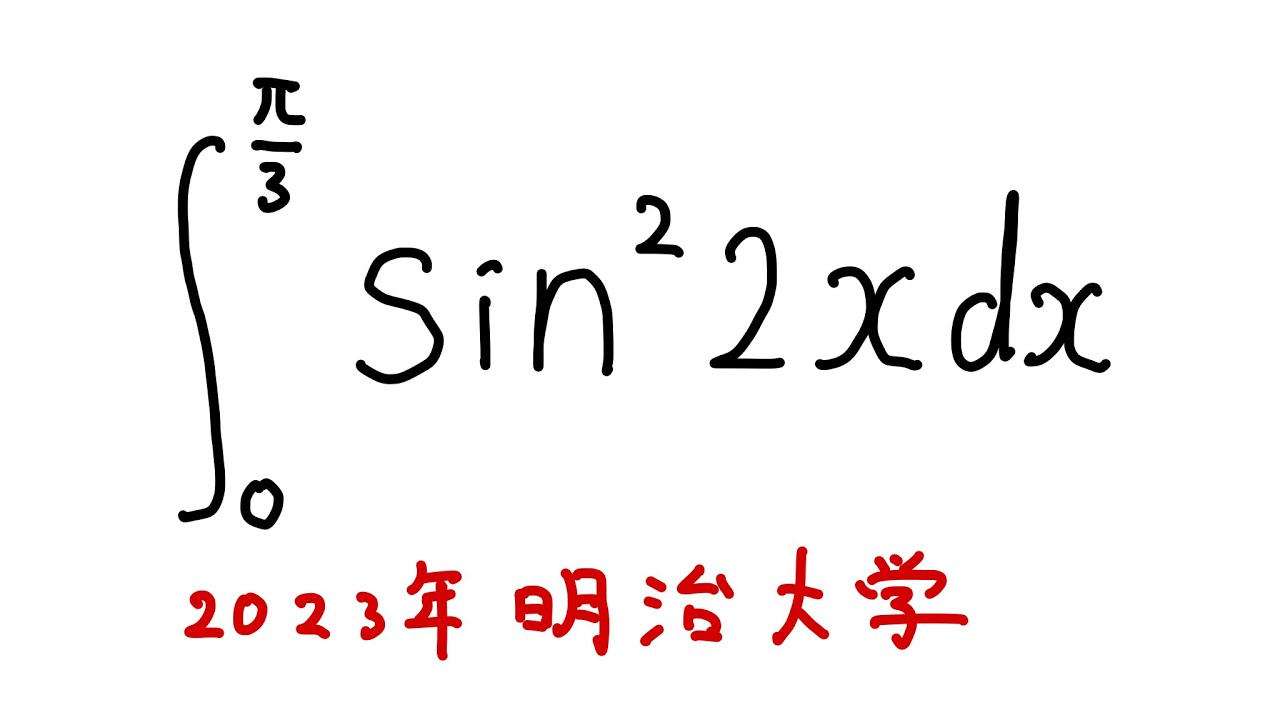ただの計算問題

問題文全文(内容文)：
計算せよ
$
\\
(\frac{1+\sqrt{13}}{2})^7+(\frac{1
-\sqrt{13}}{2})^7

$

単元： #大学入試過去問(数学)

指導講師：鈴木貫太郎

問題文全文(内容文)：
計算せよ
$
\\
(\frac{1+\sqrt{13}}{2})^7+(\frac{1
-\sqrt{13}}{2})^7

$

投稿日：2023.10.07

＜関連動画＞

数学「大学入試良問集」【1−3 背理法・対偶】を宇宙一わかりやすく

単元： #数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)

指導講師：ハクシ高校【数学科】良問演習チャンネル

問題文全文(内容文)：
次の問いに答えよ。
（1）
　（ⅰ）$\sqrt{ 2 }$が無理数であることを証明せよ。
　（ⅱ）実数$a$が$a^3+\alpha+1=0$を満たすとき、$\alpha$が無理数であることを証明せよ。

（2）
　（ⅰ）$n$を自然数とするとき、$n^3$が$3$の倍数ならば、$n$は$3$の倍数のなることを証明せよ。
　（ⅱ）$\sqrt[ 3 ]{ 3 }$が無理数であることを証明せよ。

この動画を見る　

福岡教育大　連立漸化式

単元： #大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：
$a_1=2,b_1=1$
$a_{n+1}=a_n-8b_n$
$b_{n+1}=a_n+7b_n$

出典：1989年福岡教育大学　過去問

この動画を見る　

#明治大学2023#定積分_24#元高校教員

単元： #大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{3}} \sin^2 2x dx$

出典：2023年明治大学

この動画を見る　

数学「大学入試良問集」【2−3 方程式と整数解】を宇宙一わかりやすく

単元： #大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#愛媛大学

指導講師：ハクシ高校【数学科】良問演習チャンネル

問題文全文(内容文)：
$p,q$を整数とし、$f(x)=x^2+px+q$とおく。
（1）
有理数$a$が方程式$f(x)=0$の一つの解ならば、$a$は整数であることを示せ。

（2）
$f(1)$も$f(2)$も$2$で割り切れないとき、方程式$f(x)=0$は整数の解を持たないことを示せ。

この動画を見る　

公式を使う？使わない？富山大　積分基本問題

単元： #数Ⅱ#微分法と積分法#面積、体積#数学(高校生)#富山大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
2023富山大学
a>0
$f(x)=x^3-6x$,$g(x)=-3x+a$
f(x)とg(x)は２つの共有点をもつ
①aの値
②f(x)とg(x)とで囲まれる面積

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> ただの計算問題

＜関連動画＞

数学「大学入試良問集」【1−3 背理法・対偶】を宇宙一わかりやすく

福岡教育大 連立漸化式

#明治大学2023#定積分_24#元高校教員

数学「大学入試良問集」【2−3 方程式と整数解】を宇宙一わかりやすく

公式を使う？使わない？富山大 積分基本問題