【中学数学】1次関数の基礎～分からない人はこれを見ろ～ 3-1【中２数学】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中２数学 > 1次関数 > 【中学数学】1次関数の基礎～分からない人はこれを見ろ～ 3-1【中２数学】

【中学数学】1次関数の基礎～分からない人はこれを見ろ～ 3-1【中２数学】

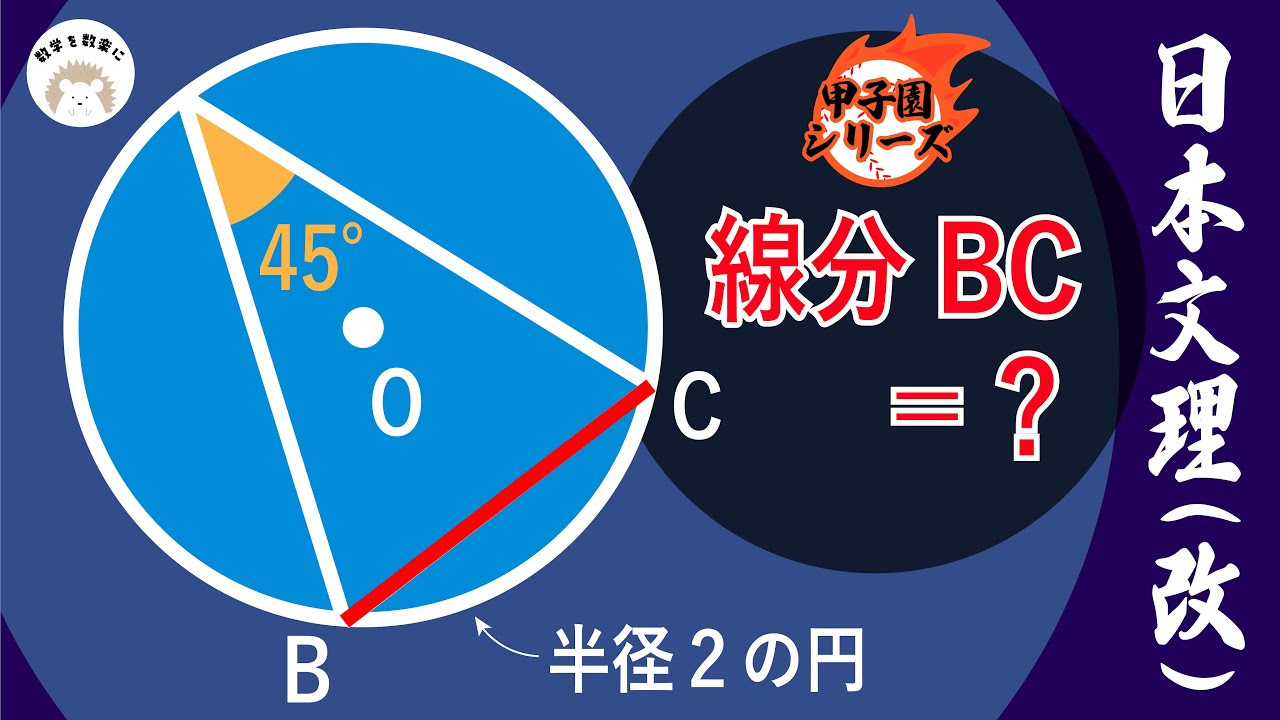
問題文全文(内容文)：
1次関数の式を求めよ

(1)傾き2で、x=4のとき,y=3
(2)変化の割合が5で点(3,2)を通る
(3)(2,-1)(4,-13)を通る
チャプター：

00:00 はじまり

00:23 基礎の話

04:20 例題演習

09:39 まとめ

10:08 まとめノート

単元： #数学(中学生)#中２数学#1次関数
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1次関数の式を求めよ

(1)傾き2で、x=4のとき,y=3
(2)変化の割合が5で点(3,2)を通る
(3)(2,-1)(4,-13)を通る
投稿日：2021.08.05

＜関連動画＞

中学生の解き方　高校生の解き方　　日本文理

アイキャッチ画像
単元： #数学(中学生)#中２数学#中３数学#円#三角形と四角形#高校入試過去問(数学)
指導講師： 数学を数楽に
問題文全文(内容文)：
円の半径=2
線分BC=？
＊図は動画内参照

日本文理高等学校（改）
この動画を見る　

割れろ割れろ割れろ割れろ割れろ割れた

アイキャッチ画像
単元： #数学(中学生)#中２数学#式の計算（単項式・多項式・式の四則計算）#高校入試過去問(数学)
指導講師： 数学を数楽に
問題文全文(内容文)：
$\frac{(2×4×6×8×10)^2 - (1×2×3×4×5)^2}{31×33}$

川端高校
この動画を見る　

【ゴリ押し用】cos72°の値と求め方を覚えよ！【語呂合わせ・導出】

アイキャッチ画像
単元： #数学(中学生)#中２数学#中３数学#数学(高校生)
指導講師： カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
cos72°の値と求め方解説動画です
-----------------
$\cos 72^{ \circ }=$
$\sin 72^{ \circ }=$
$\cos 18^{ \circ }=$
$\sin 72^{ \circ }=$
この動画を見る　

【テスト対策・中２】３章－５

アイキャッチ画像
単元： #数学(中学生)#中２数学#1次関数
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、2点$A(-3,0)、C\left(0,\dfrac{15}{4}\right)$を通る直線$\ell$と
点$B$を通る直線$m:y = - x + 6$がある。
直線$\ell.m$の交点を$P$とするとき、次の問いに答えなさい。

①直線$\ell$の式を求めよ。

②点$P$の座標を求めよ。

③$△PAB$の面積を求めよ。

④点$P$を通り、$△PAB$の面積を2等分する直線の式を求めよ。

図は動画内参照
この動画を見る　

中２数学「１次関数の利用①（１あたりの量の問題）」【毎日配信】

アイキャッチ画像
単元： #数学(中学生)#中２数学#1次関数
指導講師： 中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中2~1次関数の利用①~

例題
ある灯油を使う暖房機は、「強」と「弱」の強さがある。 それぞれの強さごとの灯油の消費量は、下の表である。
ある日、暖房機に9Lの灯油が入った状態から、はじめ は「強」、次に「弱」その後再び「強」で使用した。 下の図は、使用し始めてから父時間後の灯油の残り の量りしの関係をグラフに表したものです。

(1)使用してから四時間後の灯油の残り量を求めなさい。

(2) 4≦ｘ≦8のとき、ｙをｘの式で表しなさい。

(3)8≦x≦12のとき、ｙをｘの式で表しなさい。
この動画を見る　
PAGE TOP