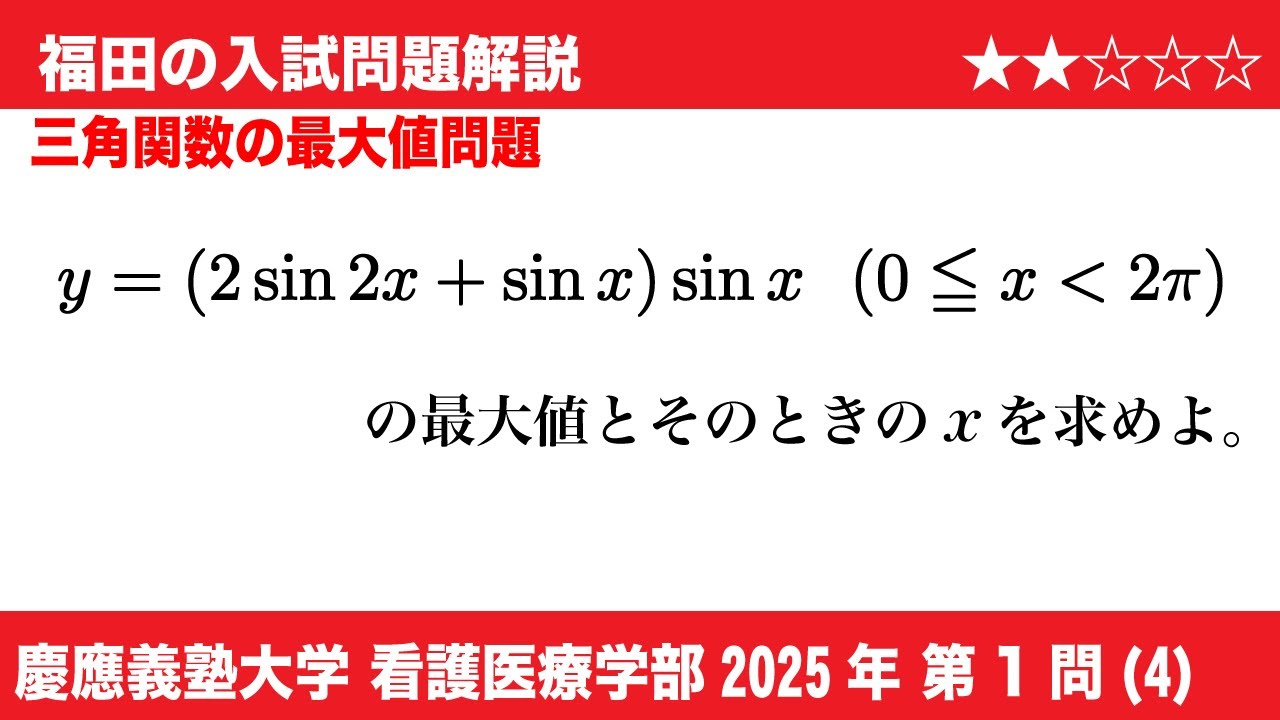
問題文全文(内容文):
次の空欄(a)~(d)を適当に補え。
(1) iを虚数単位とする。複素数$(2-i)^2$の実部は$(a)$である。
(2) $\theta$がすべての実数を動くとき、$\cos\theta+\cos2\theta$の最小値は$(b)$である。
(3) コインを5回投げて、すべて同じ面がでる確率をpとする。このとき$\log_2 p$は$(c)$である。
(4) xの関数 f(x)は$\displaystyle \int_{0}^{2}(f(t)+2t)dt=x^3+x^2+x$を満たす。このとき、$f(x)=(d)$である。
次の空欄(a)~(d)を適当に補え。
(1) iを虚数単位とする。複素数$(2-i)^2$の実部は$(a)$である。
(2) $\theta$がすべての実数を動くとき、$\cos\theta+\cos2\theta$の最小値は$(b)$である。
(3) コインを5回投げて、すべて同じ面がでる確率をpとする。このとき$\log_2 p$は$(c)$である。
(4) xの関数 f(x)は$\displaystyle \int_{0}^{2}(f(t)+2t)dt=x^3+x^2+x$を満たす。このとき、$f(x)=(d)$である。
チャプター:
0:00 オープニング
0:15 (1)の解き方
1:39 (2)の解き方
3:34 (3)の解き方
4:57 (4)の解き方
6:29 まとめ
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の空欄(a)~(d)を適当に補え。
(1) iを虚数単位とする。複素数$(2-i)^2$の実部は$(a)$である。
(2) $\theta$がすべての実数を動くとき、$\cos\theta+\cos2\theta$の最小値は$(b)$である。
(3) コインを5回投げて、すべて同じ面がでる確率をpとする。このとき$\log_2 p$は$(c)$である。
(4) xの関数 f(x)は$\displaystyle \int_{0}^{2}(f(t)+2t)dt=x^3+x^2+x$を満たす。このとき、$f(x)=(d)$である。
次の空欄(a)~(d)を適当に補え。
(1) iを虚数単位とする。複素数$(2-i)^2$の実部は$(a)$である。
(2) $\theta$がすべての実数を動くとき、$\cos\theta+\cos2\theta$の最小値は$(b)$である。
(3) コインを5回投げて、すべて同じ面がでる確率をpとする。このとき$\log_2 p$は$(c)$である。
(4) xの関数 f(x)は$\displaystyle \int_{0}^{2}(f(t)+2t)dt=x^3+x^2+x$を満たす。このとき、$f(x)=(d)$である。
投稿日:2022.01.01