問題文全文(内容文):
高校受験対策・死守89
①$-3-(-7)$を計算しなさい。
②$8-(-3)^2$を計算しなさい。
③$(-9ab^2)×2a÷(-3ab)$を計算しなさい。
④$(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})$を計算しなさい。
⑤$x^2-3x-18$を因数分解しなさい。
⑥絶対値が$4$より小さい整数の個数を求めなさい。
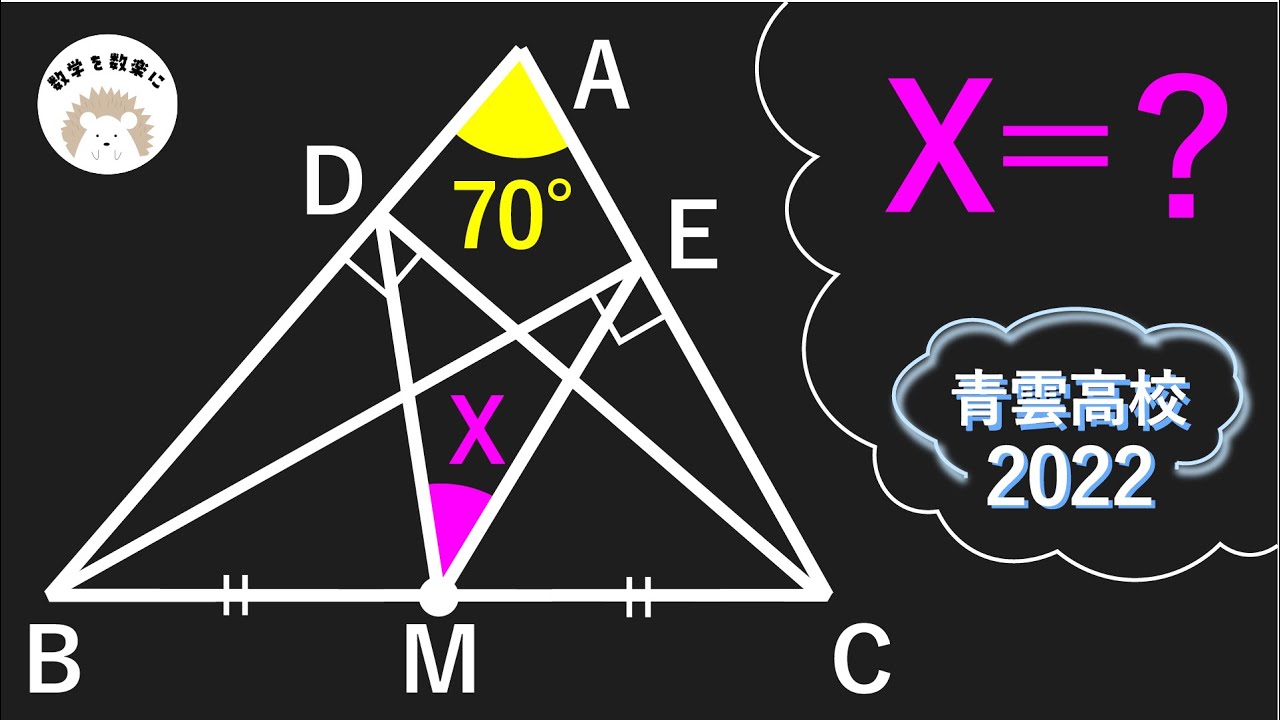
⑦右の図のア~ウは、関数$y=-2x^2、y=x^2$および$y=\frac{1}{2}x^2$のグラフを同じ座標軸を使ってかいたものです。
$y=x^2$のグラフをア~ウから一つ選びなさい。
⑧右の図のような、半径$5cm$、中心角$90°$のおうぎ形$OAB$があります。
このおうぎ形を直線$OA$を回転の軸として1回転させてできる立体の体積を求めなさい。
⑨大小2つのさいころを同時に投げるとき、出る目の数の和がちょうど$5$以下となる確率を求めなさい。
ただしさいころの$1$から$6$までの目の出方は同様に確からしいものとします。
高校受験対策・死守89
①$-3-(-7)$を計算しなさい。
②$8-(-3)^2$を計算しなさい。
③$(-9ab^2)×2a÷(-3ab)$を計算しなさい。
④$(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})$を計算しなさい。
⑤$x^2-3x-18$を因数分解しなさい。
⑥絶対値が$4$より小さい整数の個数を求めなさい。
⑦右の図のア~ウは、関数$y=-2x^2、y=x^2$および$y=\frac{1}{2}x^2$のグラフを同じ座標軸を使ってかいたものです。
$y=x^2$のグラフをア~ウから一つ選びなさい。
⑧右の図のような、半径$5cm$、中心角$90°$のおうぎ形$OAB$があります。
このおうぎ形を直線$OA$を回転の軸として1回転させてできる立体の体積を求めなさい。
⑨大小2つのさいころを同時に投げるとき、出る目の数の和がちょうど$5$以下となる確率を求めなさい。
ただしさいころの$1$から$6$までの目の出方は同様に確からしいものとします。
単元:
#数学(中学生)#中1数学#正の数・負の数#式の計算(展開、因数分解)#平方根#空間図形#確率#2次関数#円#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守89
①$-3-(-7)$を計算しなさい。
②$8-(-3)^2$を計算しなさい。
③$(-9ab^2)×2a÷(-3ab)$を計算しなさい。
④$(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})$を計算しなさい。
⑤$x^2-3x-18$を因数分解しなさい。
⑥絶対値が$4$より小さい整数の個数を求めなさい。
⑦右の図のア~ウは、関数$y=-2x^2、y=x^2$および$y=\frac{1}{2}x^2$のグラフを同じ座標軸を使ってかいたものです。
$y=x^2$のグラフをア~ウから一つ選びなさい。
⑧右の図のような、半径$5cm$、中心角$90°$のおうぎ形$OAB$があります。
このおうぎ形を直線$OA$を回転の軸として1回転させてできる立体の体積を求めなさい。
⑨大小2つのさいころを同時に投げるとき、出る目の数の和がちょうど$5$以下となる確率を求めなさい。
ただしさいころの$1$から$6$までの目の出方は同様に確からしいものとします。
高校受験対策・死守89
①$-3-(-7)$を計算しなさい。
②$8-(-3)^2$を計算しなさい。
③$(-9ab^2)×2a÷(-3ab)$を計算しなさい。
④$(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})$を計算しなさい。
⑤$x^2-3x-18$を因数分解しなさい。
⑥絶対値が$4$より小さい整数の個数を求めなさい。
⑦右の図のア~ウは、関数$y=-2x^2、y=x^2$および$y=\frac{1}{2}x^2$のグラフを同じ座標軸を使ってかいたものです。
$y=x^2$のグラフをア~ウから一つ選びなさい。
⑧右の図のような、半径$5cm$、中心角$90°$のおうぎ形$OAB$があります。
このおうぎ形を直線$OA$を回転の軸として1回転させてできる立体の体積を求めなさい。
⑨大小2つのさいころを同時に投げるとき、出る目の数の和がちょうど$5$以下となる確率を求めなさい。
ただしさいころの$1$から$6$までの目の出方は同様に確からしいものとします。
投稿日:2021.12.27