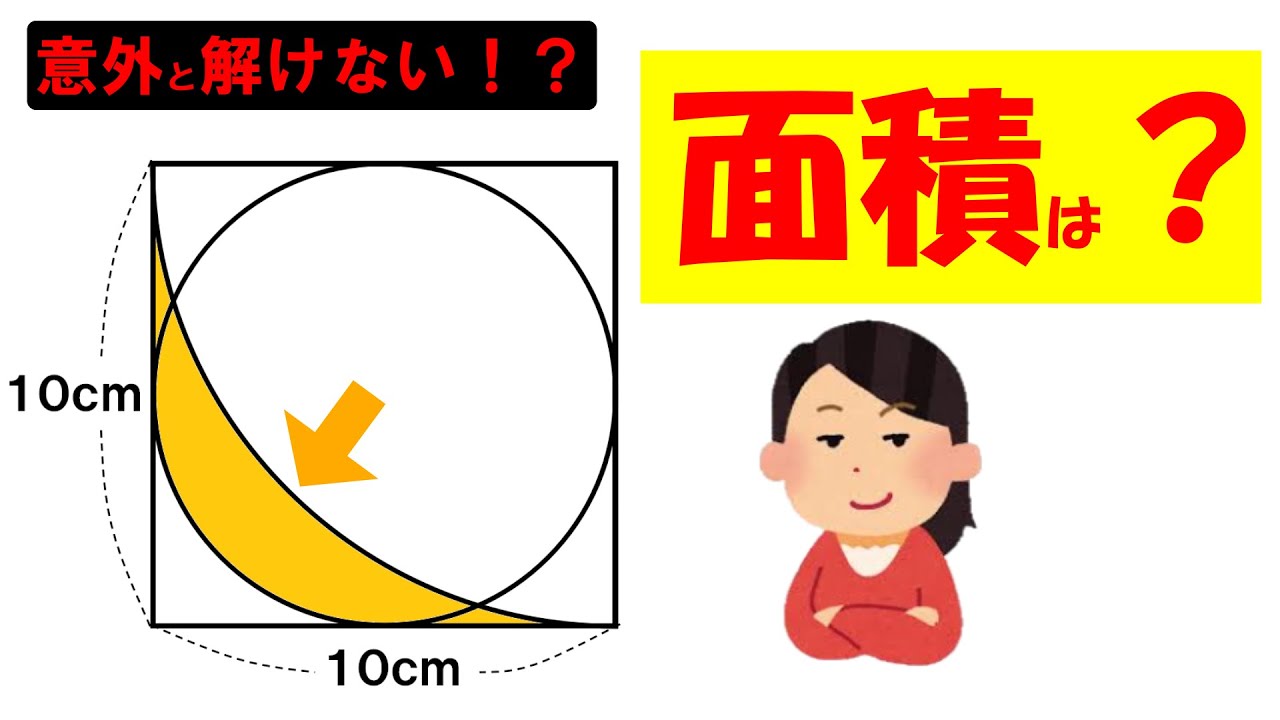
問題文全文(内容文):
面積=$\sqrt 6 + \sqrt 3 + \sqrt 2 +1$
ア=? イ=? ウ=?(ア、イ、ウは自然数)
*図は動画内参照
成田高等学校
面積=$\sqrt 6 + \sqrt 3 + \sqrt 2 +1$
ア=? イ=? ウ=?(ア、イ、ウは自然数)
*図は動画内参照
成田高等学校
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
面積=$\sqrt 6 + \sqrt 3 + \sqrt 2 +1$
ア=? イ=? ウ=?(ア、イ、ウは自然数)
*図は動画内参照
成田高等学校
面積=$\sqrt 6 + \sqrt 3 + \sqrt 2 +1$
ア=? イ=? ウ=?(ア、イ、ウは自然数)
*図は動画内参照
成田高等学校
投稿日:2021.04.30