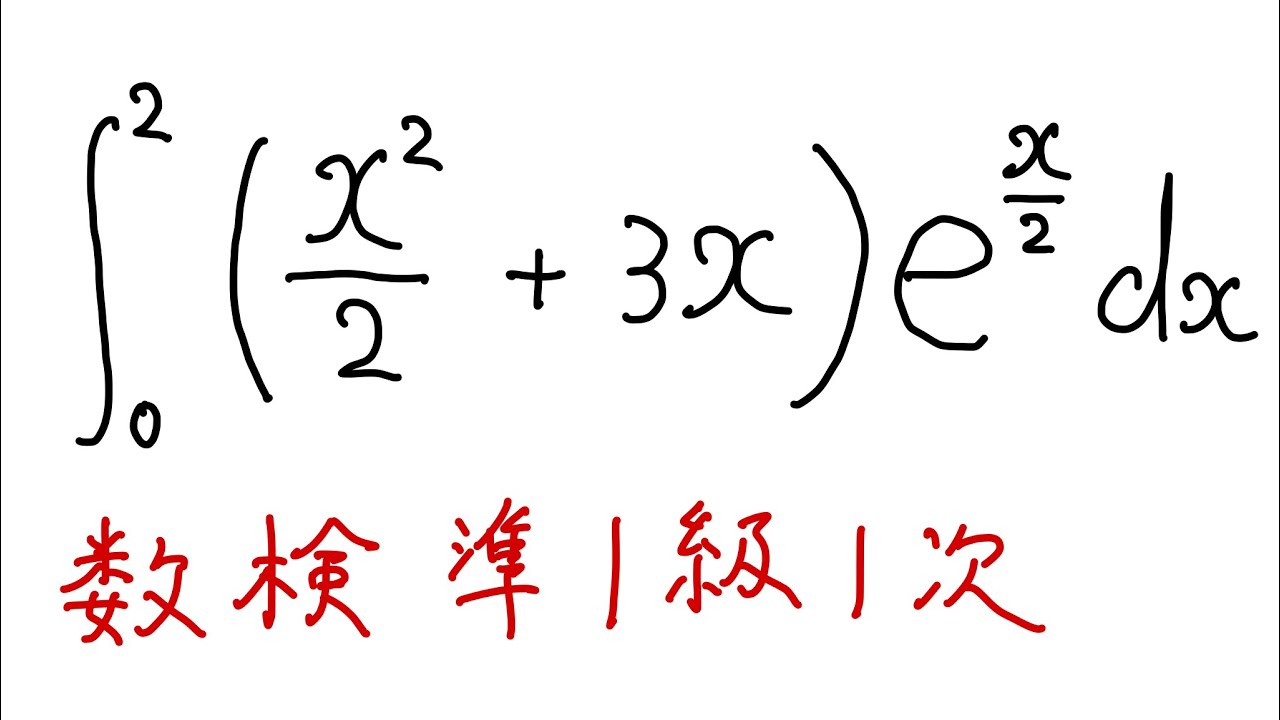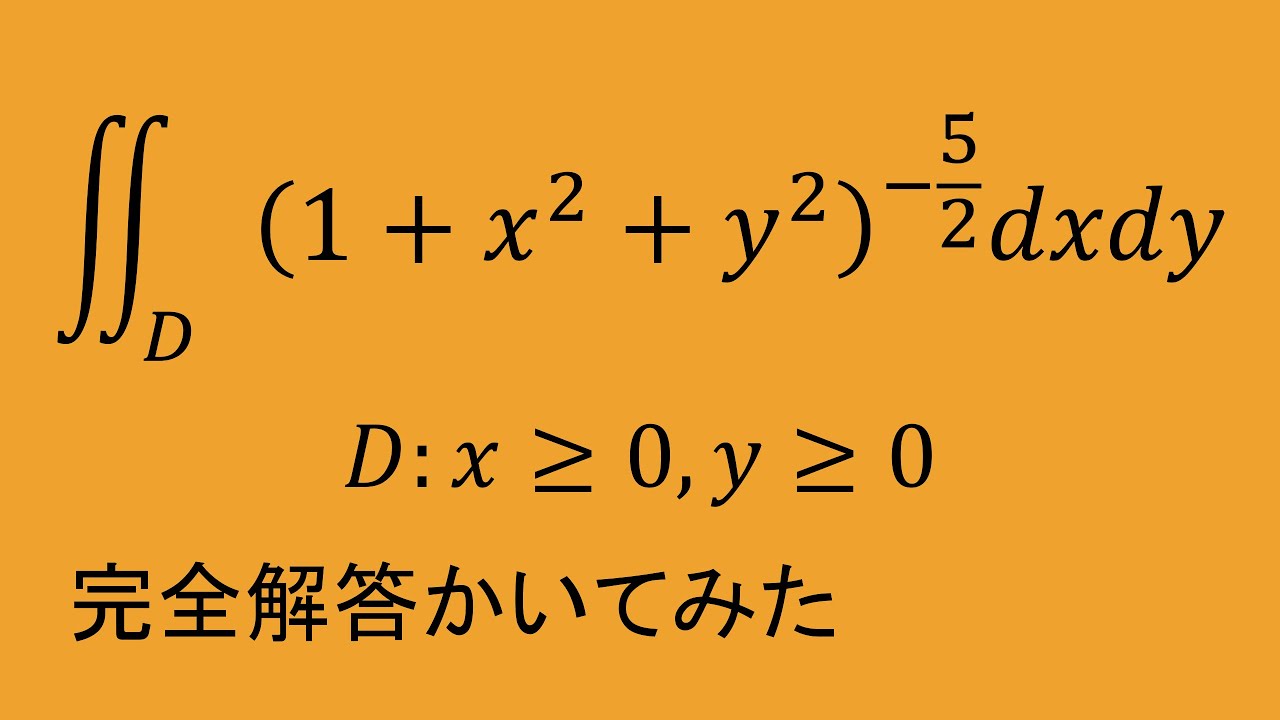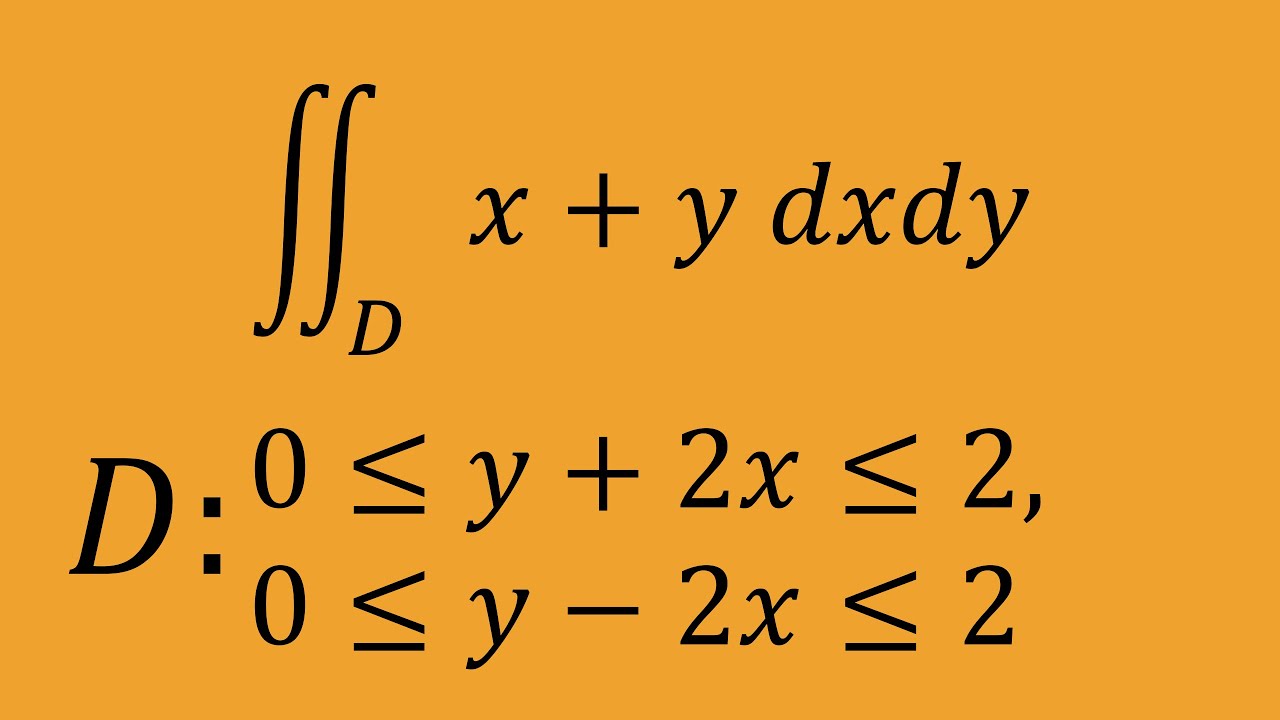【数検2級】数学検定2級2次問題3 - 質問解決D.B.（データベース）

【数検2級】数学検定2級2次　問題3

問題文全文(内容文)：
問題3.(選択)
　xy平面上において、点Pが円$x^2+y^2＝4$上を動くとき、点Ａ(3,1)と点Ｐを結ぶ線分APの中点Qの軌跡を求めなさい。

チャプター：

0:00 問題3について
0:34 解説
1:44 解き方の手順
4:56 まとめ

単元： #数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定2級

指導講師：理数個別チャンネル

問題文全文(内容文)：
問題3.(選択)
　xy平面上において、点Pが円$x^2+y^2＝4$上を動くとき、点Ａ(3,1)と点Ｐを結ぶ線分APの中点Qの軌跡を求めなさい。

投稿日：2023.02.18

＜関連動画＞

#67数学検定1級1次「こんな問題で時間使いたくない」　#因数分解

単元： #数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級

指導講師：ますただ

問題文全文(内容文)：
$xy(x^2-y^2)+yz(y^2-z^2)+zx(z^2-x^2)$を因数分解せよ

出典：数検1級1次

この動画を見る　

【数検2級】数学検定2級2次　問題4

単元： #数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定2級

指導講師：理数個別チャンネル

問題文全文(内容文)：
問題4.(選択)
AB＝5,BC＝6,CA＝4である△ABCの内接円の中心をIとします。また、直線AIと辺BCの交点をDとします。
このとき、→AB＝→b　,→AC＝→cとして、次の問いに答えなさい。
(1)　→ADを→b,→cを用いて表しなさい。
(2)　→AIを→b,→cを用いて表しなさい。

この動画を見る　

#66数学検定1級1次過去問「怖いのは計算ミスのみ」　#式変形

単元： #数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級

指導講師：ますただ

問題文全文(内容文)：
$(1-\sqrt[ 3 ]{ 2 }+\sqrt[ 3 ]{ 4 })^3$を簡単にせよ

出典：数検1級1次

この動画を見る　

重積分⑧-4【一般の変数変換】（高専数学　微積II，数検1級1次解析対応）

単元： #数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)

指導講師：ますただ

問題文全文(内容文)：
これを解け.

$\iint_D \\ \dfrac{2x-y}{x+y}dx\ dy$
$D:1\leqq x+y \leqq 2,1\leqq 2x-y \leqq 3$

この動画を見る　

微分方程式④-1【同次形】（高専数学　数検1級）

単元： #数学検定・数学甲子園・数学オリンピック等#微分とその応用#数学検定#数学検定1級#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
(1)$\frac{dx}{dt}=\frac{x}{t}-\frac{2t}{x}$
(2)$\frac{dx}{dt}=\frac{x}{t}+cos^2\frac{x}{t}$
(3)$\frac{dx}{dt}=\frac{x}{t}+e^{-\frac{x}{t}}$

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 【数検2級】数学検定2級2次 問題3

＜関連動画＞

#67数学検定1級1次「こんな問題で時間使いたくない」 #因数分解

【数検2級】数学検定2級2次 問題4

#66数学検定1級1次過去問「怖いのは計算ミスのみ」 #式変形

重積分⑧-4【一般の変数変換】（高専数学 微積II，数検1級1次解析対応）

微分方程式④-1【同次形】（高専数学 数検1級）