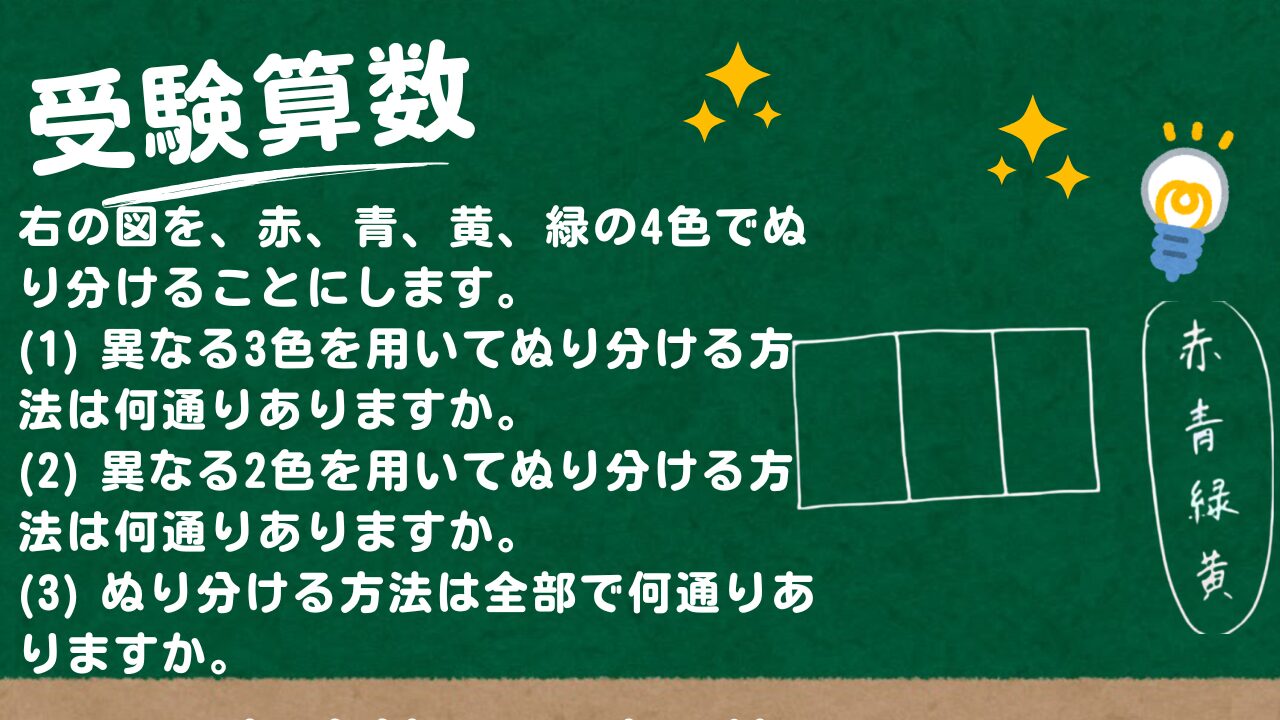
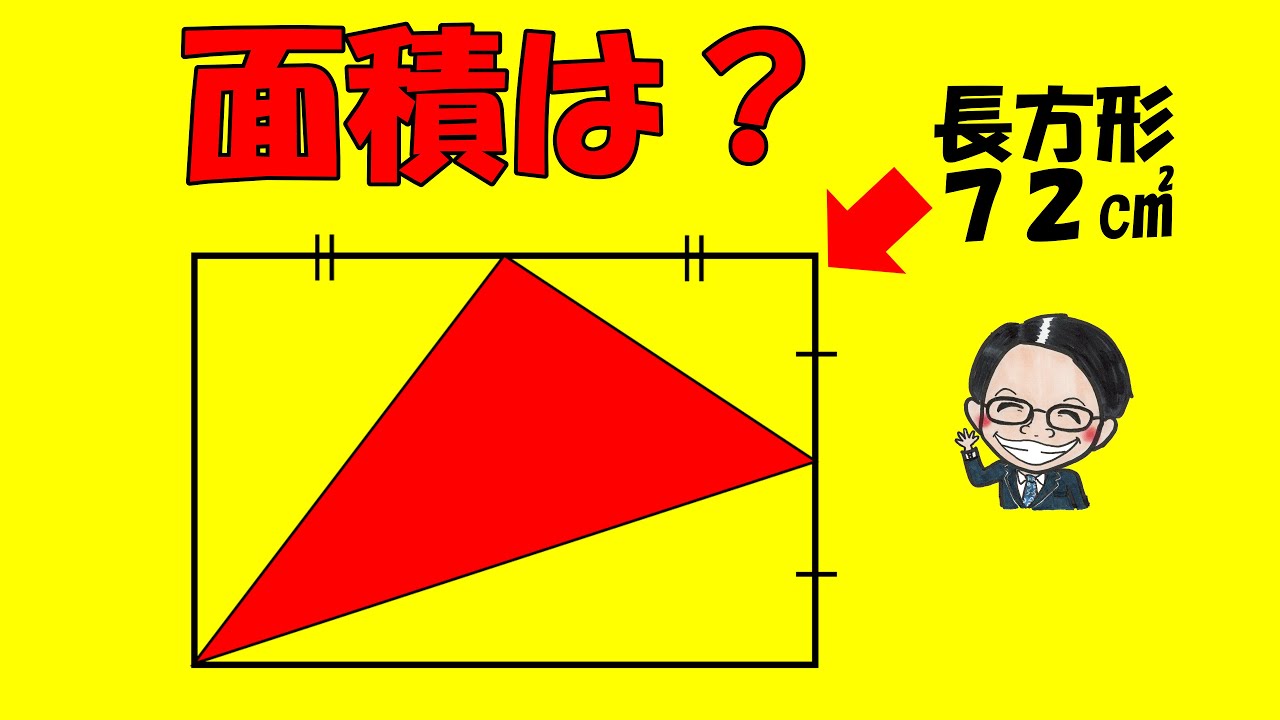
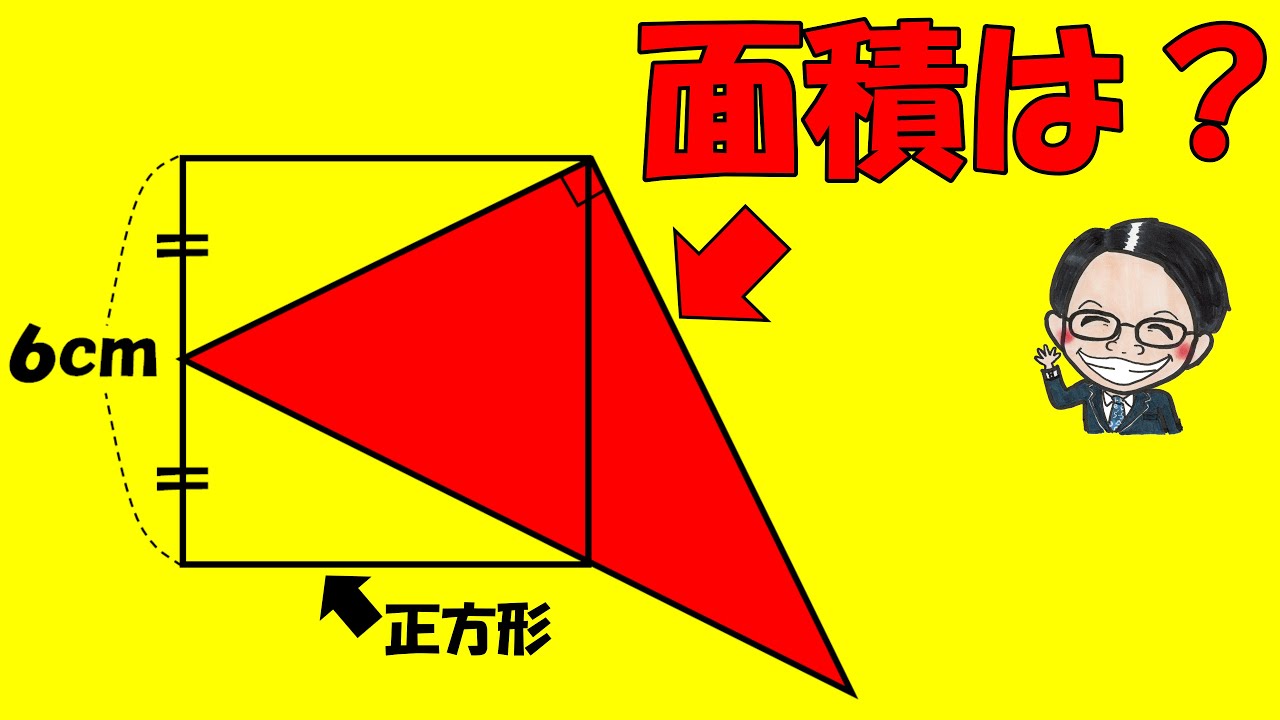
問題文全文(内容文):
例1 外側と内側の正六角形の面積比は?
例2 外側と内側の正六角形の面積比は?
単元卒業テスト
下図は面積が72㎠の正六角形ABCDEFで2点G,Hは対角線AD,AE,BFの交点です。
四角形DEHGの面積は?
*図は動画内参照
例1 外側と内側の正六角形の面積比は?
例2 外側と内側の正六角形の面積比は?
単元卒業テスト
下図は面積が72㎠の正六角形ABCDEFで2点G,Hは対角線AD,AE,BFの交点です。
四角形DEHGの面積は?
*図は動画内参照
チャプター:
0:00 オープニング
0:08 導入
1:05 正六角形の均等分割4パターン
2:32 なぜ均等に分けていると言えるのか?
10:37 例題1
12:15 例題2
15:17 単元卒業テスト 問題提示
16:00 単元卒業テスト 問題解説
18:03 まとめ
18:19 家庭教師のアスピレーション 生徒募集のご案内
18:47 おすすめ動画紹介(ピアノ演奏付き)
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
こばちゃん塾
問題文全文(内容文):
例1 外側と内側の正六角形の面積比は?
例2 外側と内側の正六角形の面積比は?
単元卒業テスト
下図は面積が72㎠の正六角形ABCDEFで2点G,Hは対角線AD,AE,BFの交点です。
四角形DEHGの面積は?
*図は動画内参照
例1 外側と内側の正六角形の面積比は?
例2 外側と内側の正六角形の面積比は?
単元卒業テスト
下図は面積が72㎠の正六角形ABCDEFで2点G,Hは対角線AD,AE,BFの交点です。
四角形DEHGの面積は?
*図は動画内参照
投稿日:2023.02.10