【中1 数学】中1-71 作図③ ~さらに応用編~

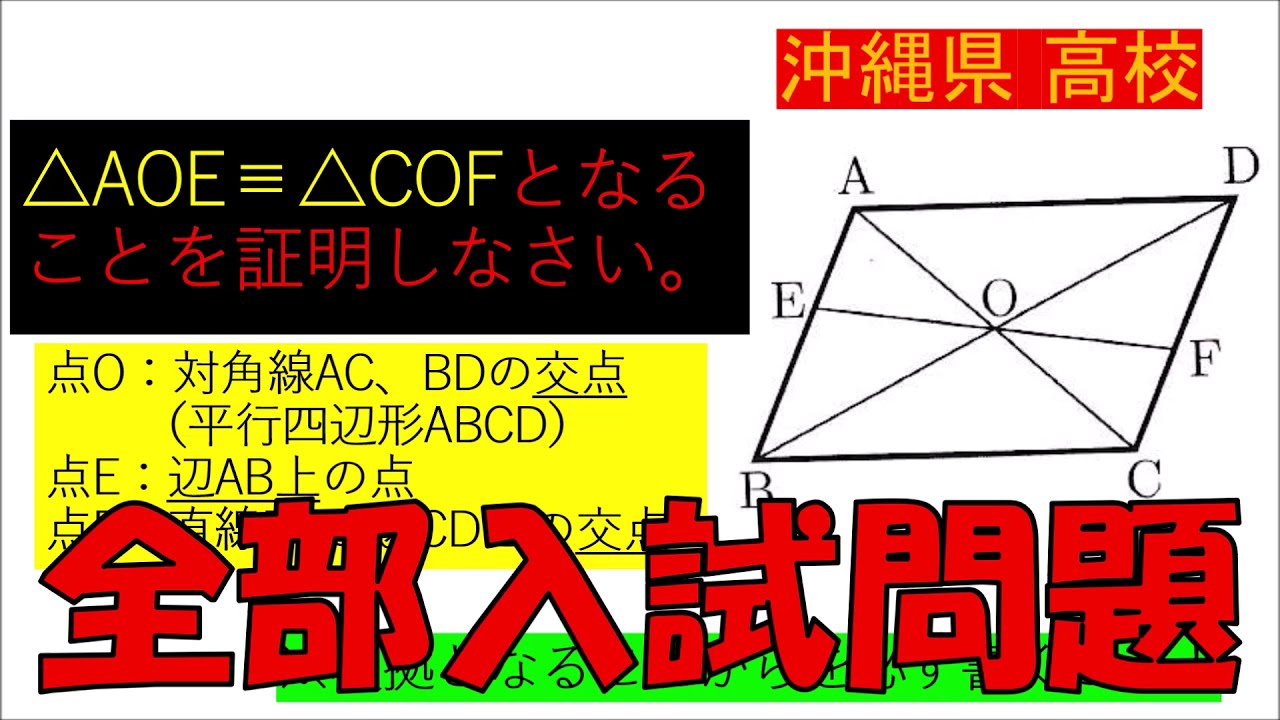
問題文全文(内容文)：
①長方形ABCDにおいて、頂点Bが頂点Dに重なるように折るとき、折り目の線分を作図しよう！

②2点A,Bから等しい距離にあり、かつ点Cに最も近い点Pを作図しよう！

③$\angle AOC$の二等分線OPと$\angle BOC$の二等分線OQを作図しよう！

④③のように作図したとき$\angle POQ$は何度？
※図は動画内参照

単元： #数学(中学生)#中１数学#平面図形

指導講師：とある男が授業をしてみた

投稿日：2013.12.04

＜関連動画＞

【題意を式で表せ！】整数：法政大学高等学校～全国入試問題解法

単元： #数学(中学生)#中１数学#方程式#文字と式#高校入試過去問(数学)#法政大学高等学校

指導講師：高校入試から見た数学の世界「全部入試問題」by しろたん

問題文全文(内容文)：
$ \color{red}{整数a}$を$ \color{red}{7}$で割ると$ \color{red}{4}$余り,$ \color{red}{整数b}$を$ \color{red}{7}$で割ると$ \color{red}{3}$余る.

$ \color{orange}{a^2+2ab}$を$ \color{orange}{7}$で割ったときの$ \color{orange}{余り}$を求めなさい.

法政大高校過去問

この動画を見る　

ただの一次方程式

単元： #数学(中学生)#中１数学#方程式

指導講師：鈴木貫太郎

問題文全文(内容文)：
$ \dfrac{x-3}{2021}+ \dfrac{x}{2022}+ \dfrac{x+3}{2023}=9$
これを解け.

この動画を見る　

【学問に王道なし！】整数：福岡大学附属大濠高等学校～全国入試問題解法

単元： #数学(中学生)#中１数学#文字と式#高校入試過去問(数学)#福岡大学附属大濠高等学校

指導講師：高校入試から見た数学の世界「全部入試問題」by しろたん

問題文全文(内容文)：
$ n $は正の整数であり, $ a,b,c,d $は整数である.
$ n=(a^2-1)(b^2-2)\times(c^2-3)(d^2-4)$

このような$ \color{red}{nの値}$で最小の値は$ \Box $である.

福岡大学附属大濠高等学校過去問

この動画を見る　

【テスト対策中1】6章-4

単元： #数学(中学生)#中１数学#空間図形#立体図形#立体切断

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
◎次の立体の表面積を求めなさい。

①正四角錐

②円柱

③円錐

この動画を見る　

【テスト対策中1】4章-3

単元： #数学(中学生)#中１数学#比例・反比例

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
変数$x$のとる値が次の場合に、$x$の変域を不等号を使って表しなさい。

①$-2$より大きく$5$以下

②$-4$以上$7$未満

③$3$より小さい

④$-8$以上

⑤$2$より$7$より小さい

⑥$-1$未満

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 【中1 数学】中1-71 作図③ ~さらに応用編~

＜関連動画＞

【題意を式で表せ！】整数：法政大学高等学校～全国入試問題解法

ただの一次方程式

【学問に王道なし！】整数：福岡大学附属大濠高等学校～全国入試問題解法

【テスト対策 中1】6章-4

【テスト対策 中1】4章-3