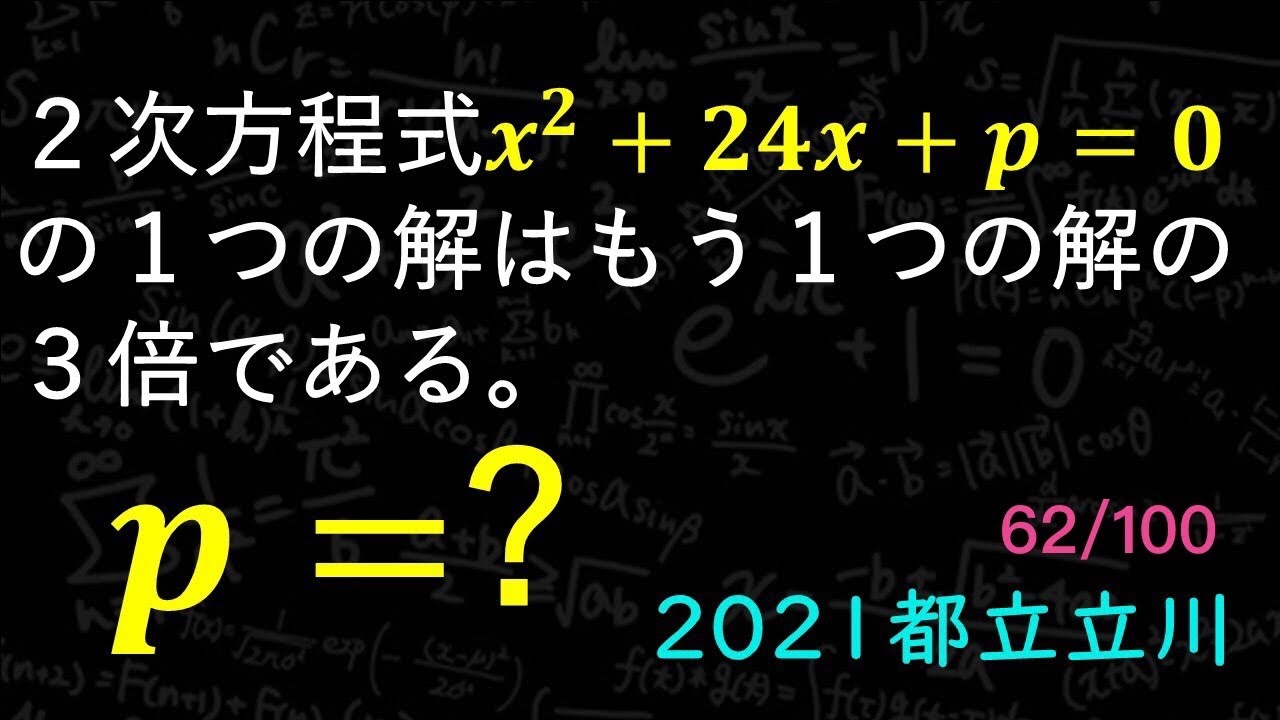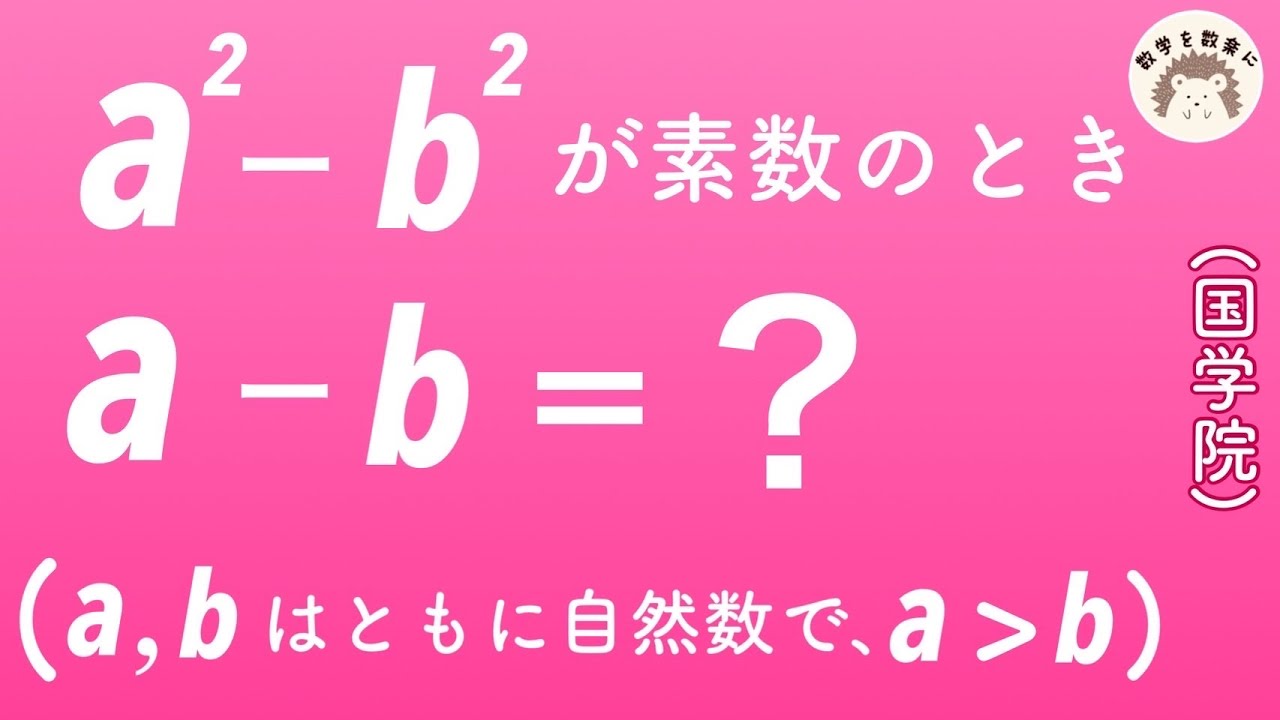問題文全文(内容文):
高校受験対策・規則性8
Q.
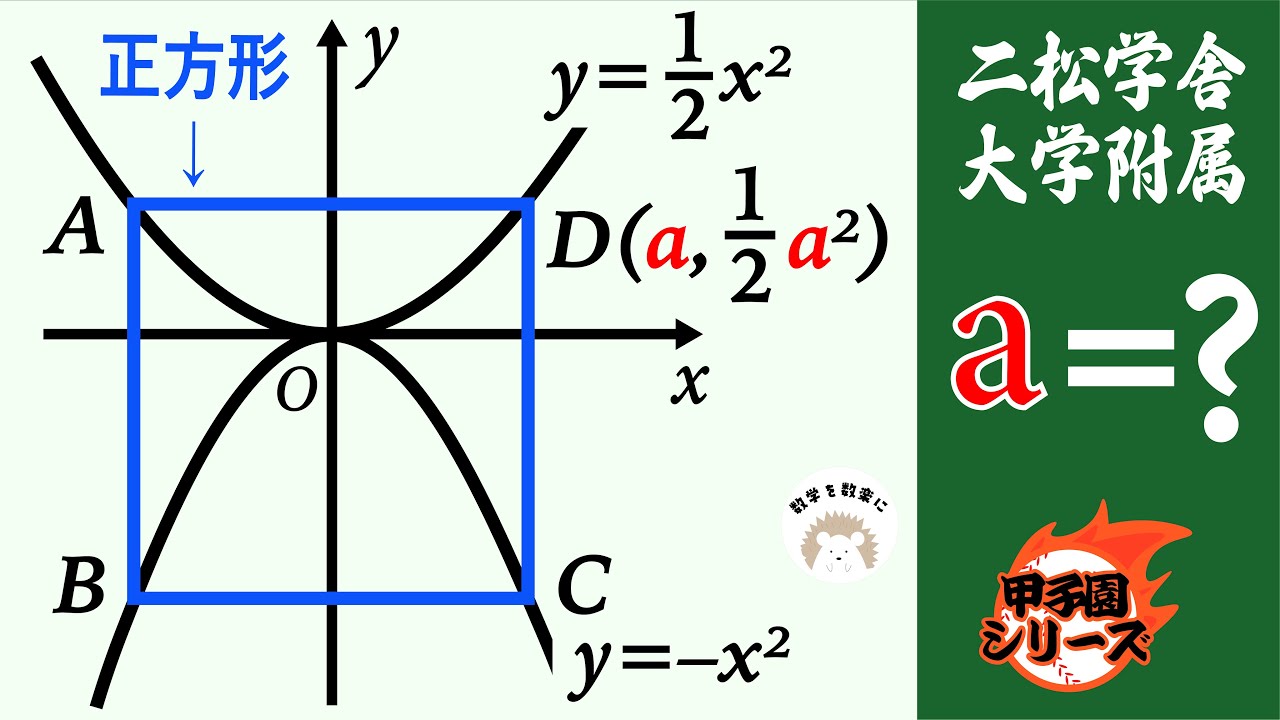
形も大きさも同じ半径1cmの円盤がたくさんある。
これらを図1のように、縦m枚、横n枚(m,nは3以上の整数)の長形状に並べる。
このとき4つの角にある円盤の中心を結んでできる図形は長方形である。
さらに図2のように、それぞれの円盤は$x$で示した、点で他の円盤と接しており、ある円盤が接している円盤の枚数をその円盤に書く。
例えば、図2はm=3、n=4の長方形状に円盤を並べたものであり、
円盤Aは2枚の円盤と接しているので、円盤Aに書かれる数は2となる。
同様に円盤Bに 書かれる数は3、円盤Cに書かれる数は4となる。
また、m=3、n=4の長方形状に円盤を並べた とき、すべての円盤に他の円盤と押している枚数をそれぞれ書くと、図3のようになる。
①m=4、n=5のとき、3が書かれた円盤の枚数を求めなさい。
②m=5、n=6のとき、円盤に書かれた数の合計を求めなさい。
③m=$x$、n=$x$のとき、円盤に書かれた数の合計は440であった。
このとき$x$の値を求めなさい。
④の文のⅠ、Ⅱ、Ⅲに当てはまる数を求めなさい。ただしa,bは20以上の整数で、a \lt bとする。
m=a+1、n=b+1として、円盤を図1のように並べる。
4つの角にある円盤の中心を結んでできる長方形の面積が780$cm^2$となるとき、
4が書かれた円盤の枚数はa=(Ⅰ)、b=(Ⅱ)のとき最も多くなり、その枚数は(Ⅲ)枚である。
高校受験対策・規則性8
Q.
形も大きさも同じ半径1cmの円盤がたくさんある。
これらを図1のように、縦m枚、横n枚(m,nは3以上の整数)の長形状に並べる。
このとき4つの角にある円盤の中心を結んでできる図形は長方形である。
さらに図2のように、それぞれの円盤は$x$で示した、点で他の円盤と接しており、ある円盤が接している円盤の枚数をその円盤に書く。
例えば、図2はm=3、n=4の長方形状に円盤を並べたものであり、
円盤Aは2枚の円盤と接しているので、円盤Aに書かれる数は2となる。
同様に円盤Bに 書かれる数は3、円盤Cに書かれる数は4となる。
また、m=3、n=4の長方形状に円盤を並べた とき、すべての円盤に他の円盤と押している枚数をそれぞれ書くと、図3のようになる。
①m=4、n=5のとき、3が書かれた円盤の枚数を求めなさい。
②m=5、n=6のとき、円盤に書かれた数の合計を求めなさい。
③m=$x$、n=$x$のとき、円盤に書かれた数の合計は440であった。
このとき$x$の値を求めなさい。
④の文のⅠ、Ⅱ、Ⅲに当てはまる数を求めなさい。ただしa,bは20以上の整数で、a \lt bとする。
m=a+1、n=b+1として、円盤を図1のように並べる。
4つの角にある円盤の中心を結んでできる長方形の面積が780$cm^2$となるとき、
4が書かれた円盤の枚数はa=(Ⅰ)、b=(Ⅱ)のとき最も多くなり、その枚数は(Ⅲ)枚である。
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・規則性8
Q.
形も大きさも同じ半径1cmの円盤がたくさんある。
これらを図1のように、縦m枚、横n枚(m,nは3以上の整数)の長形状に並べる。
このとき4つの角にある円盤の中心を結んでできる図形は長方形である。
さらに図2のように、それぞれの円盤は$x$で示した、点で他の円盤と接しており、ある円盤が接している円盤の枚数をその円盤に書く。
例えば、図2はm=3、n=4の長方形状に円盤を並べたものであり、
円盤Aは2枚の円盤と接しているので、円盤Aに書かれる数は2となる。
同様に円盤Bに 書かれる数は3、円盤Cに書かれる数は4となる。
また、m=3、n=4の長方形状に円盤を並べた とき、すべての円盤に他の円盤と押している枚数をそれぞれ書くと、図3のようになる。
①m=4、n=5のとき、3が書かれた円盤の枚数を求めなさい。
②m=5、n=6のとき、円盤に書かれた数の合計を求めなさい。
③m=$x$、n=$x$のとき、円盤に書かれた数の合計は440であった。
このとき$x$の値を求めなさい。
④の文のⅠ、Ⅱ、Ⅲに当てはまる数を求めなさい。ただしa,bは20以上の整数で、a \lt bとする。
m=a+1、n=b+1として、円盤を図1のように並べる。
4つの角にある円盤の中心を結んでできる長方形の面積が780$cm^2$となるとき、
4が書かれた円盤の枚数はa=(Ⅰ)、b=(Ⅱ)のとき最も多くなり、その枚数は(Ⅲ)枚である。
高校受験対策・規則性8
Q.
形も大きさも同じ半径1cmの円盤がたくさんある。
これらを図1のように、縦m枚、横n枚(m,nは3以上の整数)の長形状に並べる。
このとき4つの角にある円盤の中心を結んでできる図形は長方形である。
さらに図2のように、それぞれの円盤は$x$で示した、点で他の円盤と接しており、ある円盤が接している円盤の枚数をその円盤に書く。
例えば、図2はm=3、n=4の長方形状に円盤を並べたものであり、
円盤Aは2枚の円盤と接しているので、円盤Aに書かれる数は2となる。
同様に円盤Bに 書かれる数は3、円盤Cに書かれる数は4となる。
また、m=3、n=4の長方形状に円盤を並べた とき、すべての円盤に他の円盤と押している枚数をそれぞれ書くと、図3のようになる。
①m=4、n=5のとき、3が書かれた円盤の枚数を求めなさい。
②m=5、n=6のとき、円盤に書かれた数の合計を求めなさい。
③m=$x$、n=$x$のとき、円盤に書かれた数の合計は440であった。
このとき$x$の値を求めなさい。
④の文のⅠ、Ⅱ、Ⅲに当てはまる数を求めなさい。ただしa,bは20以上の整数で、a \lt bとする。
m=a+1、n=b+1として、円盤を図1のように並べる。
4つの角にある円盤の中心を結んでできる長方形の面積が780$cm^2$となるとき、
4が書かれた円盤の枚数はa=(Ⅰ)、b=(Ⅱ)のとき最も多くなり、その枚数は(Ⅲ)枚である。
投稿日:2019.11.04