問題文全文(内容文)：
次の方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y +1= 0 \\
3x + y +9= 0
\end{array}
\right.
\end{eqnarray}$

活水高等学校過去問

問題文全文(内容文)：
$m^2-n^2=16$を満たす自然数m,nを求めなさい

函館白百合学園高校過去問

問題文全文(内容文)：
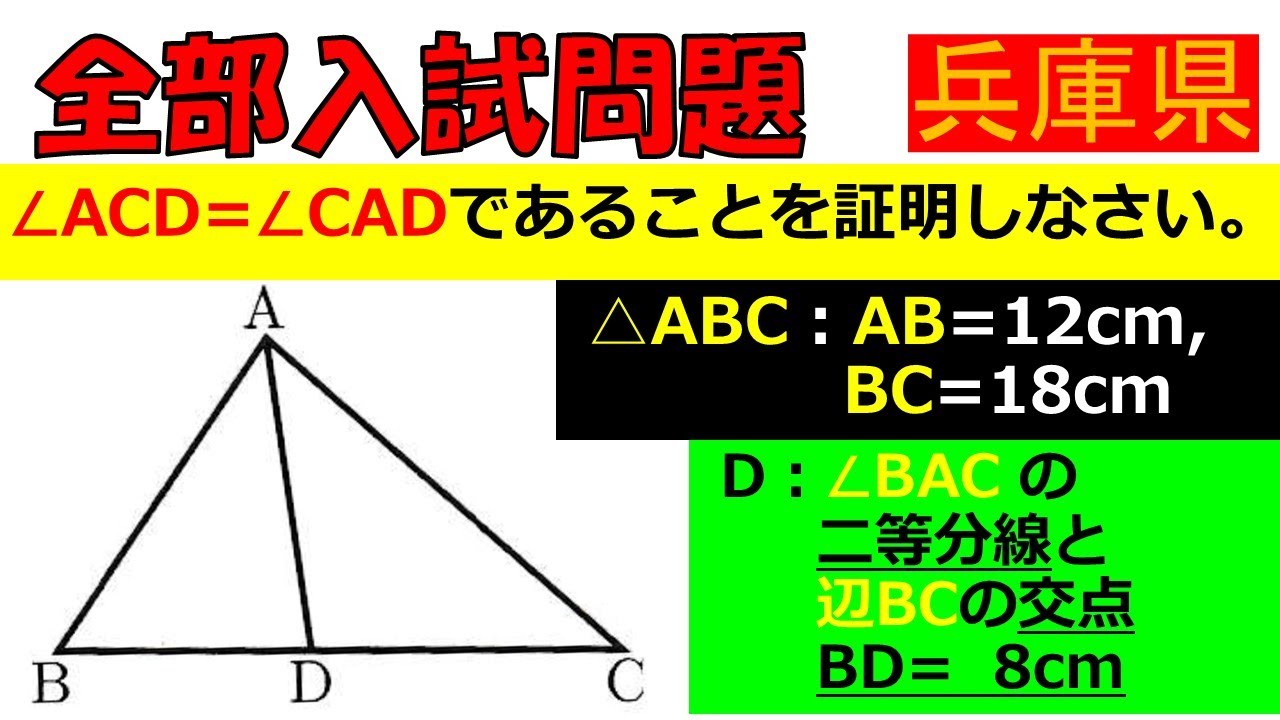
$ \triangle ABC $の$ AB$は12cmであり,$ BC $は18cmである.
$ D $は$ \angle BAC $の二等分線と辺$ BC $の交点である.
$ \angle ACD=\angle CAD $であることを証明しなさい.

兵庫県公立高等学校過去問

問題文全文(内容文)：
$ n $を自然数とするとき,$ 5-\dfrac{78}{n}$の値が自然数となるような
最も小さい自然数$ n $の値を求めなさい.

大阪府公立高等学校過去問

問題文全文(内容文)：
2次方程式$ (x+2)^2+x^2=(x+4)^2-12 $を解きなさい.

法政大学第二高等学校過去問

問題文全文(内容文)：
$ n $を自然数とする.
$ n \leqq \sqrt x \leqq n+1 $を満たす自然数$ x $の個数が100であるときの
$ n $の値を求めなさい.

大阪府公立高等学校過去問

問題文全文(内容文)：
$ x,y $についての連立方程式　$ \begin{eqnarray}
\left\{
\begin{array}{l}
4x+3y=11 \\
x-ky=-\dfrac{1}{2}k
\end{array}
\right.
\end{eqnarray}$　の解が　$\begin{eqnarray}
\left\{
\begin{array}{l}
x=p \\
y=q
\end{array}
\right.
\end{eqnarray}$ であり,
$ p+q=3 $が成り立つ.$ k $の値を求めなさい.

明治大学付属中野高等学校過去問

問題文全文(内容文)：
$ (1+\sqrt2+\sqrt4+\sqrt8+\sqrt{16}+\sqrt{32})$
$ \times (1-\sqrt2+\sqrt4-\sqrt8+\sqrt{16}-\sqrt{32}$
を計算しなさい.

洛南高等学校過去問

問題文全文(内容文)：
$ \sqrt{65}-5 $の整数部分を$ n $とし,小数部分を$ t $とする.
(1)$ n $はいくつか?
(2)$ \dfrac{1}{4}t^2+4t=\Box $である.

東海高校過去問

問題文全文(内容文)：
直線$ y=-\dfrac{1}{2}x+10 $上の点で
$ x $座標も$ y $座標も正の整数である点は全部で$ \Box $個ある.

福岡大学付属大濠高等学校過去問

問題文全文(内容文)：
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2-4y^2-10x+25=0　･･･① \\
x^2+x-6-2xy+4y=0･･･②
\end{array}
\right.
\end{eqnarray}$
上式が成り立つ$ x,y $の組をすべて求めよ.

明治大学付属明治高等学校過去問

問題文全文(内容文)：
$ a=2(\sqrt{13}-2)$の$ b $は整数部分であり,$ c $は小数部分である.
このとき,$ (a+3b+1)(c+1)$の値は$ \Box $である.

東海高等学校過去問

問題文全文(内容文)：
$ \dfrac{3007}{3201}$を既約分数に直すと$ \Box $である.

慶應義塾高校過去問

問題文全文(内容文)：
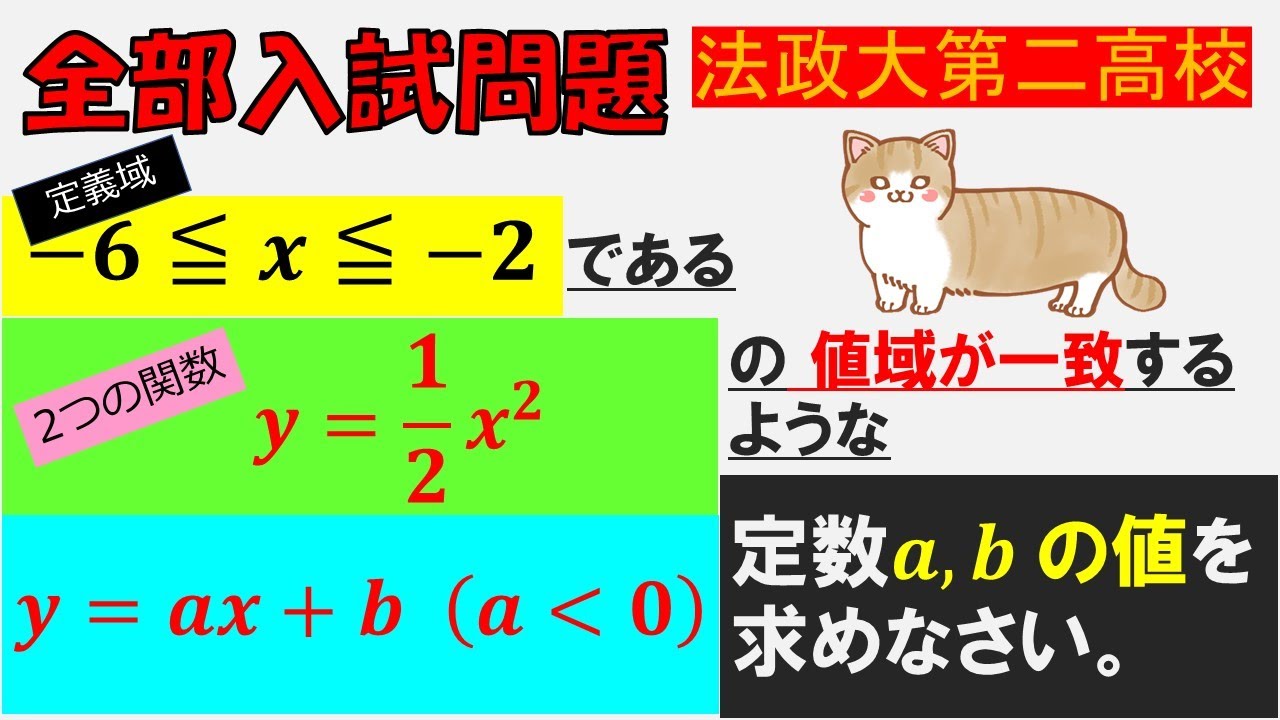
定義域$ -6 \leqq x \leqq -2 $である2つの関数
$ y=\dfrac{1}{2}x^2, y=ax+b(a \lt 0)$の値域が一致するような
定数$ a,b $の値を求めなさい.

法政大第二高校過去問

問題文全文(内容文)：
$ x(x+1)(2x+1)=0 $を満たす$ x $の値をすべて求めよ.

法政大国際高校過去問

問題文全文(内容文)：
2次方程式$ 3(3-x)=2(x-2)^2$を解け.

都立八王子東高校過去問

問題文全文(内容文)：
$ x=\sqrt7+\sqrt2 $
$ y=\sqrt7-\sqrt2 $ のとき
$ x^4-6x^2y^2+y^4 $の値を求めよ.

ラ・サール高校過去問

問題文全文(内容文)：
次の各問いに答えよ.
$\boxed{1}$(1)
$ \dfrac{(2x^3z^4)^2}{5x^2y^3}\div \left(\dfrac{x^2z^3}{y}\right)\times \left(-\dfrac{10}{xy^2}\right)$
これを計算せよ.

(2)
$ (x+2)(3x+4)=5x^2+6x+7 $
これを解きなさい.

$\boxed{2}$
図のように,放物線$ y=x^2 $上に点$ A(-1,1)$がある.
$ OA=OP$となるように$ y $軸の正の部分に点$ P $をとる.
また,直線$ AP $と放物線$ y=x^2 $の点$ A $でない交点を$ B $とする.
このとき,次の問いに答えなさい.
(1)点$ P $の座標を求めなさい.

(2)点$ B $の座標を求めなさい.

(3)点$ B $を通って,直線$ OA $に平行な直線と$ y $軸との交点を$ C $とする.
$ \triangle OAP $の面積を$ S $とするとき,
$ \triangle ABC $の面積を$ S $を用いて表しなさい.

$ \boxed{3}$
$ k $番目が$ k $である数の列$ {1,2,3,･･････}$の1番目から
$ n $番目までのすべての数の列の和を
$ \displaystyle \sum_{k=1}^{n}k $で表す.
式で表すと,$ \displaystyle \sum_{k=1}^{n}k=1+2+3+･･･+n$となる.
同様に,$ k $番目が$ k^2 $である数の列$ {1^2,2^2,3^2,･･････}$の
1番目から$ n $番目までのすべての数の列の和を式で表すと,
$ \displaystyle \sum_{k=1}^{n}k^2=1^2+2^2+3^2+･･･+n^2 $となる.
$ \displaystyle \sum_{k=1}^{5}k^3 $を式で表しなさい.

中央大学附属高等学校予想問題

問題文全文(内容文)：
$ (2x+3y)^2-3(x-3y)\times (x+3y)-4y^2 $
を因数分解しなさい.

立命館高校過去問

問題文全文(内容文)：
次の問いに答えよ.
$ \boxed{1}$
(1)
$ (\sqrt8-\sqrt{50})^3 \div \sqrt6+\sqrt{27}=? $

(2)
$ x^2y^2+5xy-24 $を因数分解しなさい.

$ \boxed{2}$
(1)
$ AB=BC=CA=6$cm,$ OA=OB=OC=6\sqrt3$cmの三角錐$OABC$がある.
$ \triangle ABC $を底面としたとき,この三角錐の高さは$ 4\sqrt6$cmである.
$ \triangle OAB $を底面としたとき,この三角錐の高さを求めなさい.

(2)
箱の中に$[1],[2],[3],[4],[5]$の5枚のカードが入っている.
この箱から,同時に2枚のカードを取り出すとき,
取り出したカードに$[3]$のカードがふくまれる確率を求めなさい.
ただし,どのカードを取り出すことも同様に確からしいものとする.

$ \boxed{3}$
$ \angle A=90°$の直角二等辺三角形の内部に,
$ PA=1,PB=\sqrt2,PC=2 $をみたす点$ P $をとり,
点$ P $と辺$ AB,BC,CA $2関して対称な点をそれぞれ$ D,E,F $とする.

(1)
$ DE,EF,FD $の長さをそれぞれ求めなさい.

(2)
五角形$ BECFD $の面積を求めなさい.

(3)
$ AB $の長さを求めなさい.

(4)
面積比$ \triangle PAB:\triangle PBC:\triangle PCA $を求めなさい.

専修大学附属高等学校予想問題

問題文全文(内容文)：
$ 230 $をある自然数$ n $で割ると余りが$ 20 $になった.
このような自然数$ n $は何個あるか.

東京都立産業技術高等専門学校過去問

問題文全文(内容文)：
2023年度の愛知県公立高校入試大問3の過去問解説です

問題文全文(内容文)：
次の問いに答えよ.

$ \boxed{1}$
三角形と四角形を組み合わせて作られた立体があり,
【図1】はその見取り図である.

【図2】から【図5】は,この立体を真上,真下,真正面,右側からみたときの図である.
$ \rhd $【図2】では四角形$ABFE,DAEI,HCAD,CGBA,$【図3】では四角形$FGHI$,
【図4】では四角形$ HCAD $,【図5】では四角形$ IDEA $は正方形である.
また,【図4】では$ \triangle AIG $,【図5】では$ \triangle AFH $は直角二等辺三角形である.

辺$ AB $の実際の長さが3cmであるとき,次の問いに答えよ.

(1)この立体の表面積を求めよ.

(2)この立体の体積を求めよ.

(3)この立体を3点$ C,H,I $をふくむ平面で2つに分ける.
面$ FGHI $をふくむ側の立体の体積を求めよ.

$ \boxed{2}$

図は,1から6までの目が書かれているさいころを1回ずつふって,
出た目の数だけコマをゴールに向かって進めるボードゲームの図である.
以下のルールに従ってコマを進めるとき,後の問いに答えよ.
ただし,後の問いは,すべてスタート地点からはじめるものとし,
さいころの1から6までの目の出方は,同様に確からしいものとする.


①出た目の数だけ駒を進める途中にゴールに着いた時は,残りのコマを戻す.
例えば,10のマスにいて,5の目が出た場合,3マス進んで2マス戻って11のマスにとまる.
②とまったマスに指示が書かれている場合は,その指示に従うものとする.
③ボードのマスに書かれている「すすむ」はゴールの方向,「もどる」はゴールと
反対方向に移動することをいう.

(1)さいころを2回ふってゴールする確率を求めよ.

(2)さいころを1回ふったとき,6の目が出た.このあと,さいころを2回ふって
ゴールするような目の出方は全部で何通りあるかを求めよ.

(3)さいころを3回ふってゴールするような目の出方は全部で
何通りあるかを求めよ.

$ \boxed{3}$

$ A,B 2$つの蛇口がついた水槽があり,$ A $からは毎分$ x $L,$ B $からは
毎分$ y $Lの水が入る.この水槽に,空の状態から$ A,B$両方使って水を入れると
5分で満水になる.

1日目,空の状態から$ A,B$両方使って水を入れ始めたが,2分後,
$ B $から入る水の量が毎分$ ((1/2)y-1)$Lに減ったため,その後
水槽が満水になるのに4分かかった.

2日目,空の状態から$ A,B$両方使って水を入れ始めたが,最初から,
$ A $からは毎分$ (3/4)x $L,$ B $からは毎分$ ((1/2)y-1)$ Lしか
水が入らなかったので,7分間水を入れても水槽が満水になるには,16L足りなかった.

このとき,$ x $と$ y $の値を求めよ.

開成高等学校予想問題

問題文全文(内容文)：
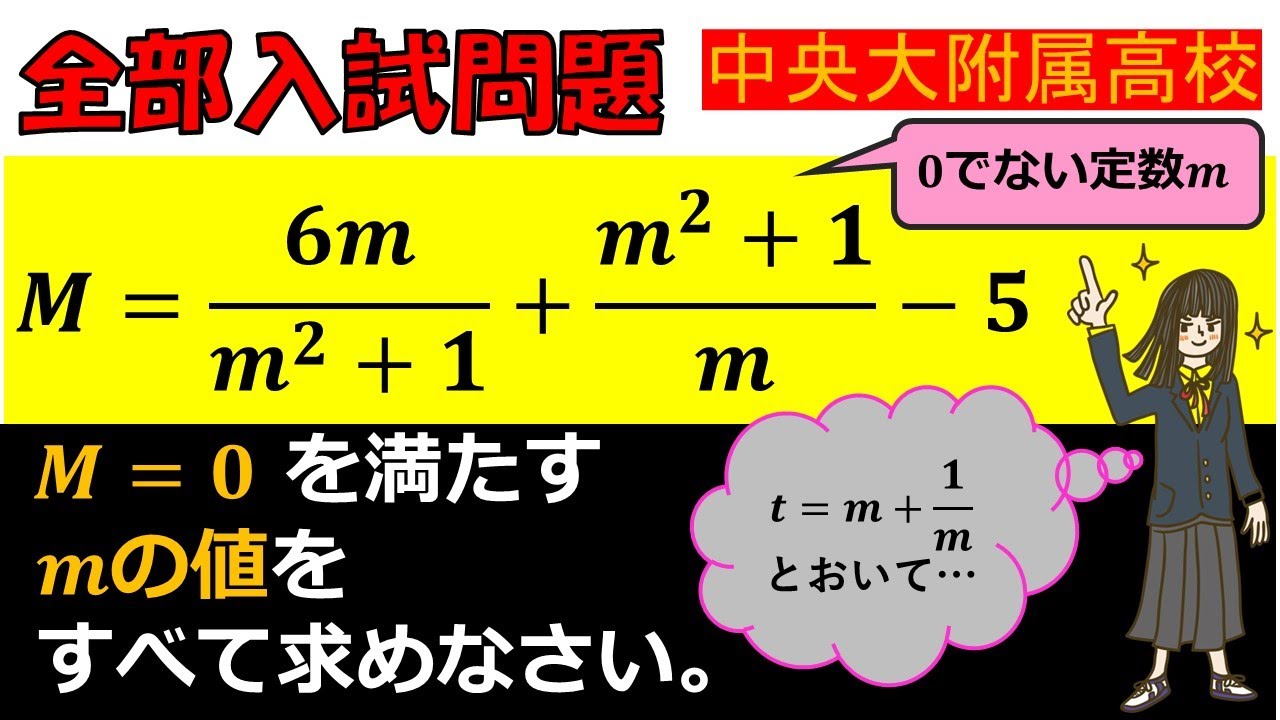
$ M=\dfrac{6m}{m^2+1}+\dfrac{m^2+1}{m}-5 $
$ M=0 $を満たす$ m $の値をすべて求めなさい.

中央大附属高校過去問

問題文全文(内容文)：
次の問いに答えよ.

$ \boxed{1}$

(1)$ \left(-\dfrac{4}{3}xy^2\right)^2\times \left(-\dfrac{9}{4}x^3y^4\right)\div \left(-\dfrac{3}{2}x^2y\right)^3 $

(2)$ \dfrac{15\sqrt2}{\sqrt6}-\dfrac{4}{\sqrt2}-\left(\dfrac{18}{\sqrt3}-\sqrt{18}\right)$

$ \boxed{2}$
連立方程式$ \begin{eqnarray}
\left\{
\begin{array}{l}
2(x+y)-3(x-4)=6 \\
\dfrac{x}{2}-\dfrac{2y-4}{3}=2
\end{array}
\right.
\end{eqnarray}$ を解け.

$ \boxed{3}$

立方体の6つの面をぬり分けるとき,次の場合のぬり分け方は何通りあるか.
ただし,回転して一致するぬり分け方は同じと見なす.

(1)赤,青,黄,緑,黒,白の6色をすべて使う場合

(2)赤,青,黄,緑,黒の5色をすべて使い,隣り合う面は異なる色を塗る場合

(3)赤,青,黄,緑,黒の5色をすべて使う場合

関西学院高等部予想問題

問題文全文(内容文)：
関数$ y=\dfrac{1}{4}x^2 $上に点$ A $は$ x=-2 $である,点$ B $は$ x=6 $である.
直線$ \ell $は2点$ A,B$を通る直線である.
点$ C $は関数$ y=\dfrac{1}{4}x^2 $上の点で
$ \triangle ABC=\triangle ABO $となるもの.
$ x $座標が最も大きくなるときの点$ C $の座標を求めなさい.

広大付属高校過去問

問題文全文(内容文)：
$ a $を定数とする.
$ x,y $についての連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
4y-3x=a \\
2x-3y=4
\end{array}
\right.
\end{eqnarray}$の解が$ x+y=a $を満たすとき,
定数$ a $の値を求めよ.

西大和学園高校過去問

問題文全文(内容文)：
北海道公立高校2022年数学過去問

春奈さんたちの中学校では, 3年生のA組30人全員と, B組30人全員の50m走の記録を調査 しました。 次の問いに答えなさい。
問1 図1は, A組, B組全員の記録を、 それぞれ箱ひげ図にまとめたものです。（図は動画内参照）
次の(1),(2) に答えなさい。
(1) B組の記録の第3四分位数を求めなさい
(2) データの散らばり (分布) の程度について、 図1から読みとれることとして
最も適当なものを、次のア~エから1つ選びなさい
ア範囲は, A組の方がB組よりも小さい。
イ四分位範囲は, A組の方がB組よりも大きい。
ウ平均値は, A組の方がB組よりも小さい。
エ最大値は, A組の方がB組よりも大きい。

問題文全文(内容文)：
$ \sqrt{2024-8n}$が自然数となるような正の整数$ n $のうち
最も小さい$ n $の値を求めよ.

入試予想問題(6)

問題文全文(内容文)：
$ x=2024 $
$ y=253 $　とするとき

$ x^2-7xy-8y^2 $の値を求めなさい.

入試予想問題(6)